应用设计过程的胚胎硬件细胞单元粒度优化方法

张砦， 王友仁

南京航空航天大学 自动化学院， 南京 210016

应用设计过程的胚胎硬件细胞单元粒度优化方法

张砦*， 王友仁

南京航空航天大学 自动化学院， 南京 210016

胚胎硬件的高可靠性主要由新颖的硬件体系和细胞电路结构来保障，缺乏应用设计过程的可靠性提高方法研究。分析了在应用设计过程中可调的胚胎硬件可靠性影响因素，针对细胞单元粒度不同会导致细胞面积变化从而影响细胞阵列可靠性的实际情况，对传统可靠性模型无法体现细胞面积变化的不足进行了改进，建立了新的可靠性模型。通过实例分析，总结出不同细胞单元粒度情况下的细胞阵列可靠性变化规律，进而给出细胞单元粒度优化选择方法，设计者基于该方法不需设计完整电路就能确定自身设计能力范围内获得最大可靠性的细胞单元粒度。

胚胎硬件； 可靠性分析； 电路优化； 细胞单元粒度； 可重构

具有功能重配置特点的可重构硬件已成为电子系统容错设计的主要对象之一。当前，可重构硬件容错主要由片外注入测试向量法进行故障检测，根据测试结果生成重配置数据，整个过程由片外或系统外控制，容错速度慢、算法复杂、计算量大，系统可靠性也因为难以高效利用内部冗余资源而较低，对实时性、可靠性要求高，外部控制困难的应用，如航空航天、深海、辐射、军事等领域电子系统，亟待研究片内自主控制，能自修复的新型可重构硬件及其设计方法。

胚胎硬件(Embryonics Hardware)是一种具有芯片自愈特色的新型可重构硬件，基于该硬件方法的芯片系统，具有内部自诊断、自修复逻辑，可自主触发局部动态重构完成自愈，整个过程完全由芯片按生物启发式方法进行分布控制，设计者无需做复杂的设计决策，且运算复杂度低、容错速度快。此外，由于硬件冗余发生在芯片内的电子细胞层，硬件容错代价大大减小，与传统板级外部控制下的芯片重构相比，不仅实现了自主控制，可靠性也得到大幅提高[1-4]。

胚胎硬件研究主要基于二维细胞单元阵列结构，以提高硬件资源利用率、容错修复速度和可靠性为目标，基本研究思路是模仿生物机体结构(器官、组织、细胞)和功能系统(神经系统、内分泌系统、免疫系统)工作方式，研究细胞单元的故障检测、移除和替代策略。当前胚胎硬件的研究重心是如何将仿生机制用硬件实现[4-9]，重点改进硬件体系和细胞电路结构，但作为一项高可靠性硬件类型，应用设计过程中基于可靠性分析的优化方法研究十分缺乏。Ortega和Tyrrell[10-11]在胚胎硬件研究早期分析了不同容错策略对系统可靠性的影响；林勇和罗文坚[12]分析了细胞阵列布局结构对系统可靠性的影响，但在可靠性建模中都将细胞视为固定节点，未考虑细胞内部模块受阵列规模、细胞布局和容错策略影响的情况，相关结论与实际设计结果存在较大偏差，要用于实际应用设计指导，需要建立与细胞电路设计结合更紧密、能体现多种设计因素的新可靠性模型。

胚胎硬件设计中，影响系统可靠性的主要因素包括：阵列规模、细胞单元电路(包含单元粒度大小和模块组成结构)、容错策略和细胞布局等。从可靠性角度，阵列规模、细胞模块组成结构和容错策略的影响很大，但应用设计过程是特定人员在已知芯片上实现一定系统功能，阵列总规模和细胞电路设计方法(决定了细胞组成结构和阵列容错策略)已确定，设计过程对系统可靠性的主要影响是设计者的设计能力(特点设计方法下的电路实现能力)、细胞单元粒度和细胞布局结构。本文针对最常用的容错策略和细胞布局方式，研究细胞单元粒度对系统可靠性的影响，以获取细胞单元粒度优化选择的分析方法。

1 基于二维细胞阵列结构的胚胎硬件

1.1 胚胎硬件的细胞阵列基本结构[2,4,9,13]

图1为典型的胚胎硬件二维细胞阵列及其内部结构，系统由结构相同的电子细胞以二维阵列形式构成，每个细胞与4个方向的相邻细胞有直接连线。系统功能由配置了逻辑功能的细胞(称为工作细胞)完成，未配置逻辑功能的细胞称为空闲细胞，修复是用故障工作细胞的配置数据配置空闲细胞实现功能替代。细胞内部模块根据功能不同，可分为逻辑功能模块、控制模块、配置存储器、坐标模块和输入输出布线器5大部分，功能模块实现逻辑功能，控制模块控制整个细胞的工作，配置存储器存储细胞的配置信息(类似生物DNA)，坐标模块确定选中哪部分配置信息以决定细胞具体执行的功能，输入输出布线器用以连接细胞和传送数据。

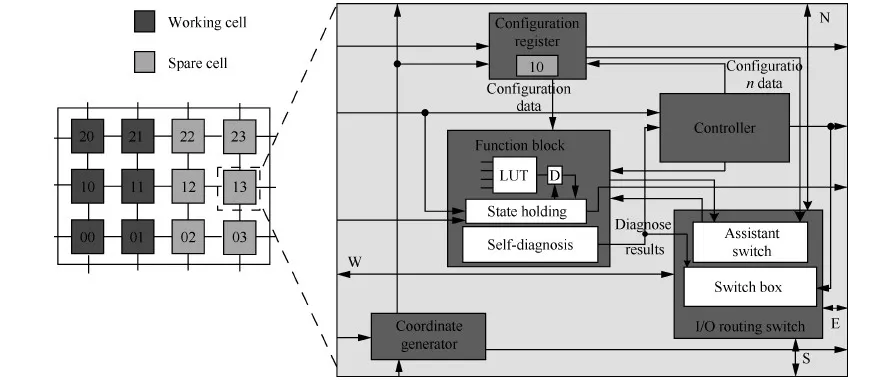
图1 胚胎硬件的二维阵列和细胞内部结构Fig.1 Cellular array and inner modules of embryonics hardware

1.2 自修复容错策略

胚胎硬件自修复是细胞自主分布式控制下实现空闲细胞对故障工作细胞替代的过程，相关方法称为自修复策略：细胞内自检测逻辑发现故障后触发细胞“死亡”，其功能由阵列中的空闲细胞代替。自修复策略研究的目标是细胞替代过程简单、涉及细胞少、细胞利用率高。目前，胚胎硬件设计采用的2种基本策略是：行/列移除和单细胞移除[4,8-13]。虽然研究人员提出过多种自修复策略，但目前尚无策略在简单性、高效性和高利用率方面均能最佳，设计中往往只能寻找最合适某种应用的策略，采用最多的是单细胞移除策略，其基本原理如图2所示，本文针对单细胞移除策略开展研究。

故障细胞所在行有空闲细胞，则先行内细胞移除：自故障细胞开始，右边细胞功能依次右移，如图2(b)所示，如果空闲细胞不少于故障细胞，行内即可完成修复；如果行内空闲细胞不足，则触发行移除操作，如图2(d)所示。

图2 单细胞移除策略工作原理Fig.2 Single-cell-elimination self-repairing strategy

1.3 基于单细胞移除策略的可靠性理论及分析[10-11]

1)k-out-of-m模型

包含m个单元，但只要其中k个单元能正常工作的系统称为满足k-out-of-m模型的系统，二维细胞阵列结构中，每个细胞相互独立，满足k-out-of-m模型。对于每个单元正常工作的概率分布函数为p(t)=e-λt的k-out-of-m模型系统，其可靠度可表示为

(1)

式中：λ为单元失效率，取常数。由于可靠度R(t)是一个随时间变化的量，一般用平均无故障时间(Mean Time to Failure，MTTF)来衡量系统可靠性，本文取λ的单位为10-6/h，则MTTF的单位为106h。

2) 基于单细胞移除策略的可靠性模型

设细胞阵列由工作细胞和空闲细胞组成，阵列总规模为N×M，工作细胞规模为n×m，其中：N、n分别为总阵列和工作细胞阵列的行数，M、m分别为总阵列和工作细胞阵列的列数。采用单细胞移除策略，每行中有m个细胞可靠则该行可靠，阵列中有n行可靠则阵列可靠，所以，单细胞移除策略下行、列的可靠性都满足k-out-of-m模型。每行可靠度为

(2)

阵列的可靠度R(t)和可靠性MTTF分别为

(3)

(4)

2 引入细胞单元粒度变化的可靠性模型

胚胎硬件由结构相同的细胞单元以阵列形式构成，细胞单元粒度的大小表明细胞能够实现逻辑功能规模。

在1.3节模型的基础上引入细胞单元粒度变量g。为说明单元粒度对细胞阵列可靠性的影响，以g=1时，N=M=200，n=m=100的方阵为例进行可靠性数值分析，g=1在实际设计中代表任选的某状态。引入单元粒度后，由于g变化会引起细胞面积变化，故以细胞数与单元粒度的乘积来表示芯片面积和细胞电路面积。

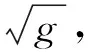
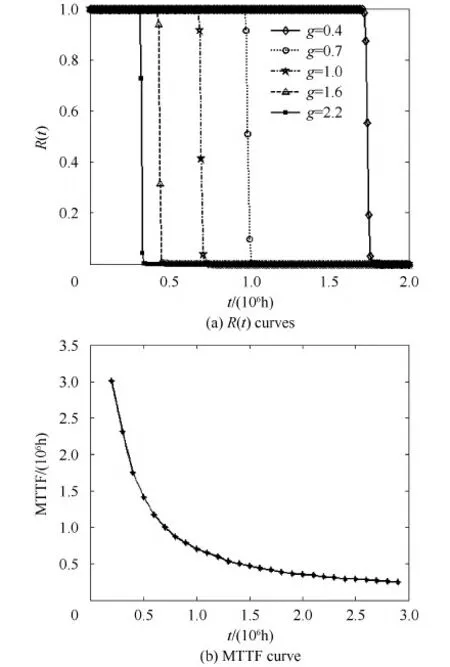
图3 阵列可靠性随细胞单元粒度g变化情况(N=M=200，n=m=100)Fig.3 Array reliability for different celludar granularity g (N=M=200，n=m=100)

由图3可知：随着g的增大，阵列可靠性单调下降，表明细胞单元粒度越小，细胞阵列可靠性越高，因此，要提高胚胎硬件的可靠性，应采用尽可能小的细胞单元粒度进行设计，且越小越好。上述分析过程将细胞单元粒度直接等效为细胞面积，存在较大的不准确性，但用于分析粒度大小对阵列可靠性的影响趋势有借鉴意义，说明通过细胞单元粒度优化选择能提高系统可靠性。

实际设计过程中，采用小细胞单元粒度设计不一定能获得高可靠性。胚胎硬件阵列中实现逻辑功能主要是细胞内的逻辑功能模块，但为了实现系统硬件自修复，细胞内还有其他模块，其硬件消耗并不与功能模块粒度大小变化成正比，当细胞单元粒度较小时，相同逻辑功能需要更多细胞单元实现，加上自修复所增加的其他模块电路，阵列连线、配置所需的硬件资源增加，采用不同细胞单元粒度设计相同系统功能，消耗的工作细胞总面积资源并不相同[7,8,15-19]，1.3节的可靠性模型无法体现自修复设计附加电路的影响。

为准确区分细胞单元粒度变化的影响，将细胞内硬件资源按是否受其影响进行分类，称细胞内仅用于实现系统逻辑功能的电路硬件为基本资源，主要是逻辑功能模块，其他资源称为辅助资源，基本资源不受阵列规模、细胞布局和自修复策略等因素影响，而辅助资源不仅受上述因素影响，还与设计者的设计能力有关。

细胞布局和容错策略一定时，辅助资源消耗主要与阵列规模和设计能力有关，细胞单元粒度小时，细胞数多，故障检测、修复控制逻辑和连线复杂度都高，导致细胞内辅助资源面积占比提高，引起系统可靠性下降。因此，考虑实际设计情况下的细胞内辅助资源因素时，小的细胞单元粒度结构会导致可靠性降低，如何反映细胞内辅助资源影响因素是新模型研究要解决的问题。

2.1 细胞硬件资源消耗分析

细胞内基本资源和辅助资源受到设计能力、设计方法和设计目标影响。

1) 基本资源

细胞单元粒度变化以细胞内基本资源变化量衡量，具体值用电路面积表示。所有工作细胞中的基本资源之和为实现系统功能的基本资源总消耗，确定的设计者，设计特定系统功能，且方法一定时，基本资源总消耗将保持不变。虽然细胞单元粒度大小不同时，基本资源总消耗会受到电路逻辑功能工艺映射算法的影响，难以精确量化，但系统逻辑功能不变。从基于查找表(LUT)结构FPGA的工艺映射过程看，采用较小粒度LUT进行逻辑分配，LUT总单元数较多而每个LUT中单元利用率较高；采用较大粒度LUT进行逻辑分配，LUT总单元数较少但每个LUT中单元利用率也较低，因此，LUT粒度大小相差不大则LUT总资源消耗相差也不会很大[20]，本文建模过程假设所有工作细胞中基本资源总消耗在实现特定系统功能时保持不变。虽然该假设存在一定误差，但利用本文优化方法进行设计时，这个误差可以通过实际工艺映射后的结果来修正，并不影响本文方法的有效性。

2) 辅助资源

细胞内主要是配置存储器和输入输出布线模块受到阵列规模、细胞布局和自修复策略影响。

① 配置存储器

细胞功能由配置存储器存储的配置信息确定，每个细胞的配置存储器需保存自身以及可能替代的所有细胞的配置信息，因此，修复次数越多，配置信息越多，配置存储器面积越大。细胞单元粒度减小，细胞数增多，可修复次数增加，则细胞内配置存储器增大，辅助资源占细胞面积比例将提高，从而影响冗余细胞数。

② 输入输出布线模块的辅助布线电路

单细胞移除策略下，修复过程行内细胞功能右移导致该行故障细胞右方所有细胞与其相邻的上下行之间的连线均发生变化[4,8,9,13]，输入输出布线器电路中须增加辅助布线电路，行内修复次数越多，细胞内的辅助布线电路将越复杂，面积越大，因此，细胞单元粒度变小会引起细胞内辅助资源面积占比提高。

2.2 改进的可靠性模型

1) 新模型的变量定义

① 应用设计过程是在固定芯片上实现特定的系统功能，芯片总面积和基本资源总面积不变。每个工作细胞面积由基本资源部分和辅助资源部分构成，细胞内基本资源部分面积大小与细胞单元粒度有关，而辅助资源面积还受到设计过程的设计能力、容错策略和阵列布局结构等影响。

② 细胞单元粒度g的初始值为g0=1。若粒度增大10%，则g=1.1，减小10%，则g=0.9。

③ 引入2.1节关于辅助资源变化的分析结果，定义每个细胞中辅助资源与细胞面积的比为β∈(0,1)，细胞内无辅助资源时，β=0。

④ 设g=1，β=0时，工作细胞数为n×m，n、m分别表示阵列中工作细胞的行数和列数；总细胞数为N×M，N、M分别表示阵列总细胞的行数和列数。

2) 新模型中的参数随细胞单元粒度变化情况

① 细胞单元面积Sg=gS/(1-β)，其中，S为g=1，β=0时的细胞面积。

④ 细胞单元失效率与细胞面积成正比：λg=g/(1-β)λ，λ=1×10-6/h是g=1时的细胞单元失效率，此处不考虑细胞内部电路形式不同引起的失效率不同问题。

2.3 基于改进模型的可靠性分析

新模型可体现细胞单元粒度g和细胞内辅助资源面积占比β对系统可靠性的影响。

选择以g=1，N=M=200，n=m=100，λ=1×10-6/h为初始状态，实际设计可任意确定初始状态，只需取该状态下的g=1即可。

1)g和β单独变化时的阵列可靠性

图4给出了g=1时，不同β值下的阵列可靠度，若g值变化，依然能获得类似的可靠度曲线，因为g一定，则工作细胞数将保持不变，单个细胞单元的面积随β增大而增大，一方面导致细胞失效率升高，另一方面总细胞数减少，而工作细胞数不变，总细胞数减少引起可修复次数减少，所以阵列可靠性单调降低(图5中g=1时的曲线给出了图4中可靠性曲线的MTTF值变化情况)。由图4和图5可知，若g保持不变，则设计的细胞电路中辅助资源越少，阵列可靠性越高，表明胚胎硬件配置存储器电路和辅助布线器电路简化设计能够有效提高阵列可靠性。

图4 g=1时，不同β下的阵列可靠度R(t)Fig.4 R(t) curves for different β when g=1

图5为不同细胞单元粒度下的阵列可靠性曲线。由图可知，g一定，系统可靠性随β增大单调递减；而β一定，可靠性将随g增大而单调降低。分析g和β单独变化对系统可靠性影响，表明减小细胞单元粒度可提高系统可靠性。

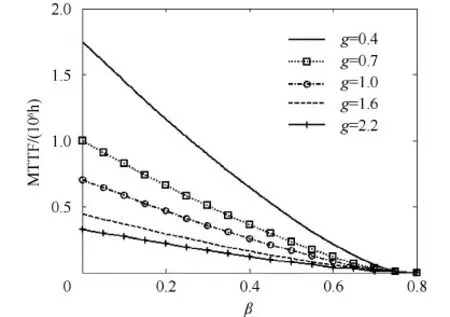
图5 不同g下，阵列可靠性随β变化情况Fig.5 Array reliability for different β and g

2)g和β同时变化时的阵列可靠性

根据2.1节内容，细胞内部电路模块变化，g和β会同时改变，只是具体变化量由设计者设计能力决定，设计者不同具体值也不同。所以还需分析不同g和β组合时的可靠性情况。

图6为细胞单元粒度g取0～2，细胞内辅助资源面积占比β为0～1时，不同g和β值下得到的阵列可靠性曲面。由图可知，g和β同时取较小值时，可靠性较高，但实际电路设计过程两者变化趋势相反，即g增大则β会减小(单元粒度大，设计难度小，辅助资源的电路占比会下降，实际情况无法做到g和β同时取较小值)，而g减小则β增大。图6的3个变量中，MTTF是优化目标，β是反应设计者设计能力的固有参数，而g是优化设计的调节手段。给出曲面中不同点的g、β取值组合，作为设计者在特定设计目标下的参数选择参照值，可选择最佳细胞单元粒度去获得设计能力范围内的最大可靠性。

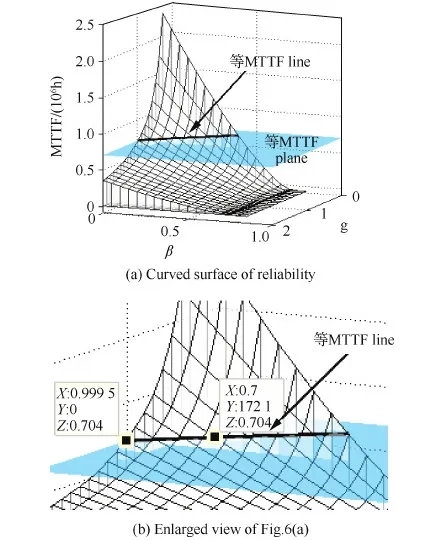
图6 g和β同时变化时的阵列可靠性曲面Fig.6 Curved surface of reliability for different g and β

图6中画出了g=1，β=0时阵列可靠性的等MTTF面和等MTTF曲线，等高线是等高面与阵列可靠性曲面的交线，等高线上点的取值为不同g和β值时获得相同可靠性的临界条件。以图中曲线为例，该曲线与g<1情况的MTTF-β曲线均有交点，为了更清晰地表示取值方法，给出了局部放大图，如图6(b)所示，其中标出了与g=0.7时MTTF-β曲线的交点，β值为0.172 1，含义为：若初始状态下g=1，β=0，则g由1降低到0.7，要保持阵列可靠性不下降，应该满足细胞内辅助资源面积占比不高于17.21%(临界值)，实用意义是：设计者设计的初始状态细胞中辅助资源面积占比为0(实际若大于0，则绘出不同初始状态下的曲面)，若希望通过减小细胞粒度的方式提高可靠性，则粒度减小30%，每个细胞中增加的辅助资源面积占比不得超过17.21%(设计者能力决定，故只能参考，无法改变)，否则采用小的细胞单元粒度也无法提高可靠性。分别计算不同g值下，等可靠性时的β值，可得到不同设计能力下的可靠性优化设计的临界条件，设计者可以此为参照，根据自身设计能力选择最佳的细胞单元粒度。该曲线与g>1的MTTF-β曲线无交点，表明如果细胞单元粒度增大，可靠性必然降低。

3) 细胞单元失效率对可靠性的影响

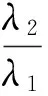
3 基于可靠性分析的胚胎硬件细胞单元粒度选择方法

1) 细胞单元粒度变化时，等可靠性设计的临界条件分析

在图6中，取不同初始状态(g=1，β取0～0.5)，分别作等MTTF线，得到相应g、β值(表1所示)，表中每行对应一种初始状态下的数据(第1行为图6中等MTTF线的值)，表1给出了g从0.5 到1.5变化时保持可靠性不下降的临界β值。

由表1可得如下结论：

① 大粒度细胞单元结构也可获得比小粒度结构更高的阵列可靠性。表中：β有临界值的情况，均表明获取相同的可靠性，设计者设计能力若大于该β临界值，则采用较大粒度能够获得更高可靠性，如第一行中，若设计者在单元粒度减小10%情况下，β值大于0.058 5，则采用g=1可获得更高可靠性。

② 表中β取值为“-”，表明采用该细胞单元粒度设计时，可靠性必然降低。初始状态下β较小时，无法采用大粒度细胞单元结构设计提高阵列可靠性，只能通过小粒度方式；初始状态下β较大时，采用大粒度细胞结构也能够获得比小粒度结构更高的可靠性。

③ 初始状态下β较小时，g增大或减小一定比例，对设计能力要求低。如β=0时，g减小10%，只要辅助资源面积比例增大不超过0.058 5-0=5.85%，可靠性将不会下降，而β=0.4时，辅助资源面积比例增大应小于0.428 0-0.4=2.8%，表明对设计能力要求更高，同时说明辅助资源越简化越有利于高可靠性设计。

2) 基于可靠性分析的硬件优化设计步骤

① 设计者根据系统设计任务，在已知系统功能和芯片的情况下，任选细胞单元粒度进行细胞电路设计：选择最常用和最擅长的细胞单元结构，此过程即确定了初始状态。

② 根据初始状态，确定可靠性模型参数：此时细胞单元粒度为g=1；根据设计完成的细胞电路计算细胞内辅助资源面积占比β(设计者不同β各不相同，通过细胞资源统计得到)；根据已设计细胞面积和芯片面积情况计算总细胞阵列的行、列细胞数；根据系统功能映射情况确定工作细胞阵列的行、列细胞数。

③ 根据步骤2获得的模型参数进行可靠性数值分析，获得与表1相似的电路优化设计的临界条件。

表1 不同初始状态下的细胞电路设计临界条件(n=m=100，N=M=200)Table 1 Thresholds of β in different initial states (n=m=100, N=M=200)

④ 根据步骤2中的g和β值选择表中的一行进行细胞单元粒度优化分析。以表1为例，设某设计的初始状态为g=1，β=0.1，则选择表中第3行数据为优化依据，表中数据的含义为：若采用比当前粒度大10%的细胞进行设计，为使系统可靠性不低于当前值(0.584)，则新细胞中辅助资源面积占比应小于0.054 6(5.46%)；若细胞单元粒度小10%，则新细胞中辅助资源面积占比应小于0.149 8(14.98%)，该行其他细胞单元粒度下的数据可以此类推，临界β值为可靠性不降低前提下的最大值，要提高可靠性β值应比临界值小。若选择不同细胞单元粒度进行细胞电路设计，并确定为初始状态，只需要根据辅助资源消耗确定相应β值，进而查找表中相应数据行进行优化分析。

⑤ 最佳细胞单元粒度选择方法：根据表中临界值，设计者根据自身能力，采用比当前细胞单元粒度大或小的细胞结构进行电路设计，比较新细胞中辅助资源面积占比与表中临界条件，可判断基于新细胞结构设计的细胞阵列的可靠性是否得到提高，进而确定最佳细胞单元粒度。

本文内容以规模为n=m=100，N=M=200的阵列为例进行可靠性数值分析，用于说明新模型分析结果对胚胎硬件设计中选择最优单元粒度的指导作用，虽然不同规模阵列的可靠性数值不尽相同，但本文方法给出的规律分析具有一般性。为了说明本文方法在不同芯片规模下实现系统功能时的适用性，表2以芯片总资源N=M=400为例，计算出了细胞电路的临界设计条件。与表1 结果相比，基本规律一致，但对设计能力要求更为宽松，如同样取g=1,β=0的初始状态，g减小10%时，保持可靠性不降低的辅助资源面积占比的增加值达7.5%。

当前，胚胎硬件设计缺乏统一的硬件结构平台和软件开发工具，采用较大粒度的细胞电路设计是应用设计的一种有效方法，可降低细粒度结构设计的实现难度，但从高可靠性设计角度，采用较小粒度细胞结构设计易于提高硬件资源利用率，在相同面积芯片上获得较高可靠性。本文从可靠性优化角度，给出了平衡大细胞粒度的低设计难度和小细胞粒度的高可靠性的分析方法，得到了细胞单元粒度选择的指导准则。设计者可在设计前根据自身设计能力设计单个细胞电路，进而通过理论分析，即可确定获得更高可靠性的设计结构。

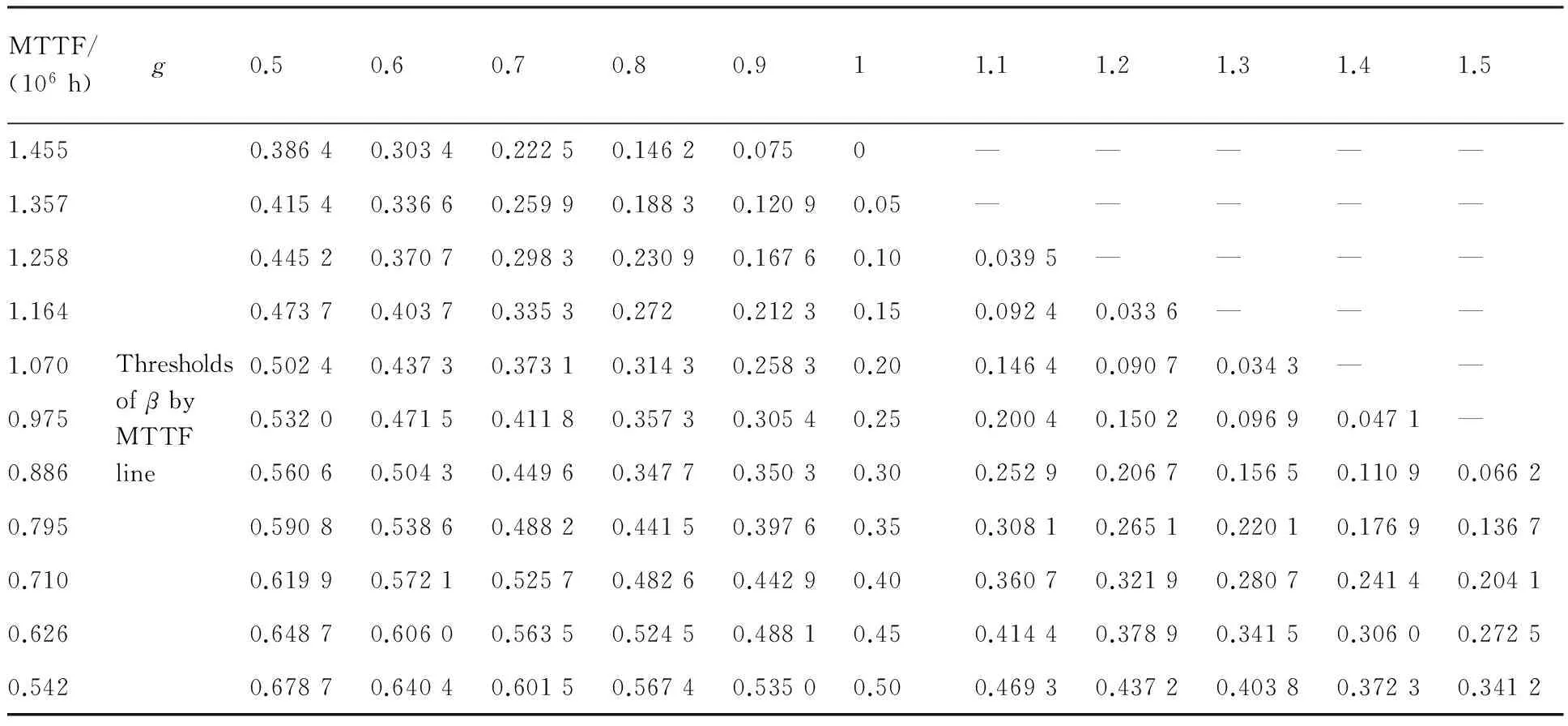
表2 不同初始状态下的细胞电路设计临界条件(n=m=100，N=M=400)Table 2 Thresholds of β in different initial states (n=m=100, N=M=400)

4 结 论

1) 针对胚胎硬件应用设计过程的电路结构特点，以可靠性分析为手段，提出了不改进硬件结构体系和电路设计方法，仅通过调节细胞单元粒度实现阵列可靠性提高的方法。

2) 分析了采用不同细胞单元粒度时细胞内电路模块的硬件资源消耗情况，引入细胞面积参数对胚胎硬件传统可靠性模型进行改进，建立了新可靠性模型。与传统可靠性模型分析结果对比，说明了新模型能够更准确地反映实际设计。

3) 给出了一种以高可靠性为优化目标的细胞单元粒度选择方法。通过实例的可靠性数值分析，总结了不同细胞单元粒度情况下的细胞阵列可靠性变化规律，给出了采用不同细胞单元粒度时获得相等阵列可靠性的细胞电路临界设计条件计算方法，总结了基于本文方法的硬件优化设计步骤。设计者只要根据自身设计能力，设计不同粒度的单个细胞电路，就能确定获得更高可靠性的最优细胞单元粒度，可避免系统电路设计的盲目性，不仅开发效率高，系统可靠性也高。

[1] BARKER W, HALLIDAY D M, THOMA Y. Fault tolerance using dynamic reconfiguration on the POEtic tissue[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(5): 666-684.

[2] MANGE D, SIPPER M, MARCHAL P. Embryonic electronics[J]. Biosystems, 1999, 51(3): 145-152.

[3] MANGE D, SIPPER M, STAUFFER A, et al. Toward robust integrated circuits: The embryonics approach[J]. Proceedings of the IEEE, 2000, 88(4): 516-543.

[4] ZHANG Z, WANG Y R, YANG S S, et al. The research of self-repairing digital circuit based on embryonic cellular array[J]. Neural Computing and Applications, 2008, 17(2): 145-151.

[5] SAMIE M, DRAGFFY G, TYRRELL A M, et al. Novel bio-inspired approach for fault-tolerant VLSI systems[J]. IEEE Transactions on Very Large Scale Integration Systems, 2013, 21(10): 1878-1891.

[6] TU H. Comparisons of self-healing fault-tolerant computing schemes[C]//2010 World Congress on Engineering and Computer Science (WCECS 2010), 2010: 87-92.

[7] ZHANG X G. Biologically inspired highly reliable electronic systems with self-healing cellular architecture[D]. Bristol: University of the West of England, 2005.

[8] 郝国锋, 王友仁, 张砦， 等. 可重构硬件芯片级故障定位与自主修复方法研究[J]. 电子学报, 2012, 40(2): 384-388.

HAO G F, WANG Y R, ZHANG Z, et al. In-chip fault localization and self-repairing method for reconfigurable hardware[J]. Acta Electronica Sinica, 2012, 40(2): 384-388 (in Chinese).

[9] 孙川, 王友仁, 张砦， 等. 可重构阵列自主容错方法研究[J]. 信息与控制, 2010, 39(5): 568-573.

SUN C, WANG Y R, ZHANG Z, et al. Self fault-tolerant reconfigurable array[J]. Information and Control， 2010, 39(5): 568-573 (in Chinese).

[10] ORTEGA C, TYRRELL A M. Self-repairing multi-cellular hardware: a reliability analysis[C]//5th European Conference on Artificial Life (ECAL), 1999: 442-446.

[11] ORTEGA C, TYRRELL A M. Reliability analysis in self-repairing embryonic systems[C]//Proceedings of the First NASA/DoD Workshop on Evolvable Hardware, 1999: 120-128.

[12] 林勇， 罗文坚.n×n阵列胚胎电子系统应用中的优化设计问题分析[J]. 中国科学技术大学学报, 2007, 37(2): 171-176.

LIN Y, LUO W J. Analysis of optimization design inn*narray embryonic system applications[J]. Journal of University of Science and Technology of China， 2007, 37(2): 171-176 (in Chinese).

[13] 张砦, 王友仁. 基于可靠性分析的胚胎硬件容错策略选择方法[J]. 系统工程理论与实践, 2013, 33(1): 236-242.

ZHANG Z, WANG Y R. Guidelines to fault-tolerant strategy selection in embryonics hardware based on reliability Analysis[J]. Systems Engineering-Theory & Practice， 2013, 33(1): 236-242 (in Chinese).

[14] 杜文志, 谭维炽. 针对FPGA内缺陷成团的电路可靠性设计研究[J]. 中国空间科学技术, 2004, 24(2): 19-26.

DU W Z, TAN W Z. Research on design of circuit reliability in FPGA with defect clustering[J]. Chinese Space Science and Technology, 2004, 24(2): 19-26 (in Chinese).

[15] GUPTA S, SHARMA A. Embryonics: A new family of coarse grained FPGA with self repair and self-reproducing properties[J]. International Journal of Electrical and Electronics Engineers, 2010, 2(1): 31-43.

[16] SEFFRIN A, BIEDERMANN A. Cellular-array implementations of bio-inspired self-healing systems: state of the art and future perspectives[J]. Design Methodologies for Secure Embedded Systems: Lecture Notes in Electrical Engineering, 2011, 78: 151-170.

[17] SZASZ C, CHINDRIS V. Development of hardware redundant embryonic structure for high reliability control applications[C]//12th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), 2010: 728-733.

[18] BREMNER P, LIU Y, SAMIE M, et al. SABRE: A bio-inspired fault-tolerant electronic architecture[J]. Bioinspiration & Biomimetics， 2013, 8(1): 1-16.

[19] XIE S D, WANG Y X. Construction of tree network with limited delivery latency in homogeneous wireless sensor networks[J]. Wireless Personal Communication, 2014, 78(1): 231-246.

[20] 徐国培. 基于LUT的FPGA工艺映射算法的设计与实现[D]. 西安： 西安电子科技大学, 2009.

XU G P. Design and implementation of technology mapping algorithm in LUT-based FPGA[D]. Xi’an: Xidian University, 2009 (in Chinese).

张砦男， 博士， 讲师。主要研究方向： 仿生硬件自修复、 可重构电子系统设计。

Tel.: 13851798450

E-mail: wolnyzhang@nuaa.edu.cn

王友仁男， 博士， 教授， 博士生导师。主要研究方向： 可重构硬件设计、 电子系统健康监测与故障诊断。

E-mail: wangyrac@nuaa.edu.cn

*Correspondingauthor.Tel.：13851798450E-mail:wolnyzhang@nuaa.edu.cn

Cellgranularityoptimizationmethodofembryonicshardwareinapplicationdesignprocess

ZHANGZhai*,WANGYouren

CollegeofAutomationEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

Thehighreliabilityofembryonicshardwareissupportedbythenovelarchitectureofreconfigurablecellulararray.Duringtheapplicationdesignprocess,researchonthemethodtoimprovethereliabilityisscarce.Inthispaper,thosefactorsadjustablebydesignerintheapplicationprocesshavebeenextractedout,whichaffectthereliabilityofembryonicshardware.Inembryonichardware,cellareawillchangeindifferentcellgranularity,whichisfollowedbythechangeofcellulararrayreliability.Tosolvethisproblem,anewreliabilitymodelisproposedforthetraditionalreliabilitymodeldoesnothaveparameterstoexpresstheareachangeofcells.Afterthereliabilityanalysisofexamples,variationlawsofcellulararrayreliabilitywithdifferentcellgranularityaresummarized,andacellgranularityoptimizationmethodisraised.Basedonthemethod,designerscanchoosetheoptimalcellgranularitywithoutacompletedesignofcellulararray.

embryonicshardware;reliabilityanalysis;circuitoptimization;cellulargranularity;reconfigurable

2015-11-27；Revised2015-12-16；Accepted2016-02-15；Publishedonline2016-02-241643

URL：www.cnki.net/kcms/detail/11.1929.V.20160224.1643.008.html

s：NationalNaturalScienceFoundationofChina(61202001,61402226)

2015-11-27；退修日期2015-12-16；录用日期2016-02-15； < class="emphasis_bold">网络出版时间

时间：2016-02-241643

www.cnki.net/kcms/detail/11.1929.V.20160224.1643.008.html

国家自然科学基金 (61202001，61402226)

*

.Tel.：13851798450E-mailwolnyzhang@nuaa.edu.cn

张砦， 王友仁． 应用设计过程的胚胎硬件细胞单元粒度优化方法J． 航空学报,2016,37(11):3502-3511.ZHANGZ,WANGYR.CellgranularityoptimizationmethodofembryonicshardwareinapplicaitondesignprocessJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3502-3511.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0041

V243.1; TP18

A

1000-6893(2016)11-3502-10