垂尾抖振主动控制的压电作动器布局优化
2016-11-20梁力杨智春欧阳炎王巍
梁力, 杨智春, 欧阳炎, 王巍
西北工业大学 航空学院 结构动力学与控制研究所, 西安 710072
垂尾抖振主动控制的压电作动器布局优化
梁力, 杨智春*, 欧阳炎, 王巍
西北工业大学 航空学院 结构动力学与控制研究所, 西安 710072
为了提高压电作动器垂尾抖振主动控制系统的控制性能,提出一种基于输出可控性的压电作动器优化准则。使用压电驱动载荷等效方法建立压电纤维复合材料(MFC)压电作动器力学模型,并建立了带MFC压电作动器垂尾结构模型的动力学方程。在模态可控性和模态价值理论的基础上,提出考虑剩余模态影响的压电作动器优化目标函数。针对垂尾结构的前5阶模态使用遗传算法优化得到压电作动器的布局方案,使用线性二次高斯(LQG)最优控制方法控制垂尾的抖振响应。仿真结果表明,本文优化得到的布局方案比用其他方法能更好地均衡系统的模态可控性,减小剩余模态的影响,获得更好的垂尾抖振响应控制。
压电作动器; 智能结构; 布局优化; 抖振; 可控性
双垂尾布局的高性能飞机在大迎角飞行时,机翼和边条翼产生的脱体分离涡通常会在到达垂尾前破裂,并形成非定常脉动扰流,激发垂尾抖振,从而对飞机的安全性和垂尾结构的疲劳寿命产生严重影响[1]。为此,研究人员采用结构振动主动控制的方法控制垂尾抖振,Moses[2]和Chen[3]等使用压电作动器对F/A-18的缩比垂尾模型进行了抖振控制的实验研究,Chen等[4]采用液压舵面和压电材料混合作动器对F/A-18垂尾模型进行了研究。在使用压电作动器控制垂尾抖振时,压电作动器布局对抖振控制效果有着至关重要的影响。不合理的作动器布局轻则降低控制系统效能,重则造成控制系统失效。因此,有必要对垂尾抖振压电主动控制系统的压电作动器布局优化展开研究。
Gupta等[5]对压电作动器的布局优化方法作了详细总结。目前对于压电作动器的布局优化方法研究大多集中在Arbel[6]、Hac和Liu[7]提出的基于系统可控/可观性Gramian矩阵的方法,其中包括Collet[8]提出的考虑系统溢出不稳定问题的优化指标、Bruant等[9-10]提出的归一化系统可控性能最大指标以及王军等[11]提出的能量吸收速率指标。这种方法虽然能够保证系统的可控性最大,但对于大阻尼和存在密集模态的结构并不适用。
Sadri等[12-13]使用Hamdan和Nayfeh[14]提出的模态可控性指标对压电板模型进行了优化,并对比了可控性Gramian矩阵和模态可控性两种方法,研究表明模态可控性方法能得到更好的优化结果,并且不受结构阻尼和模态的限制。Junkins和Kim[15]使用模态价值分析方法,结合系统响应,提出作动器最大输出可控性方法,该方法直接将作动器的布局和系统的输出联系,能更好地指导作动器布局优化。
上述研究中,对压电作动器的布局研究大多集中在简单的梁模型[6-9]和矩形板模型[10-13],并且由于压电作动器的几何外形限制,这类优化问题通常是根据作动器尺寸将结构划分为若干离散区域进行优化的[10,16-17]。对于飞机垂尾这种形状和边界相对复杂的结构,尤其对于压电纤维复合材料(MFC)这一新型压电作动器的布局优化研究较少。相比于传统的压电陶瓷作动器,MFC压电作动器具有更好的力电耦合特性和对不同外形结构的适应能力,并且由于MFC特殊的结构和各向异性的材料特性,使得这种作动器的驱动具有一定的方向性,因此,采用MFC压电作动器控制垂尾结构抖振响应时,需要对MFC压电作动器的布置位置和布置方向进行优化,从而达到更好的抖振控制效果。
本文使用MFC压电作动器控制垂尾抖振,根据输出可控性指标,提出考虑剩余模态影响的作动器优化准则,通过对MFC压电作动器形心位置的连续优化和布局方向角的离散优化得到压电作动器的优化布局方案,并采用线性二次高斯(LQG)最优控制方法对某垂尾结构的前5阶模态(前3阶为控制模态,第4、5阶为剩余模态)进行控制,通过数值算例验证了方法的有效性。
1 MFC压电智能结构动力学系统建模
使用压电驱动载荷等效方法[18]对MFC压电作动器建模,图1所示为粘贴MFC压电作动器的薄板模型,图中:Nx和Ny分别为x和y方向的压电驱动力,Mx和My分别为x和y方向的压电驱动力矩,压电作动器厚度tp远小于其长度lp和宽度wp,属于平面应力问题,法向应力σ3=0。图1中1方向为压电纤维排列和压电材料极化方向,这一类型的压电材料可在1方向提供电场强
度E1≠0,2、3方向电场强度为E2=E3=0的电场,并产生相应的压电应变。其应力-应变关系为
(1)
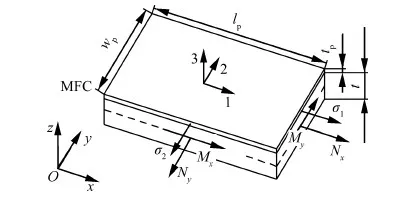
图1 MFC-薄板模型Fig.1 MFC-plate model
根据逆压电效应原理,可得压电材料产生的诱导应力为
(2)
式中:cij(i,j=1,2,3)为压电材料的弹性常数;dij为压电应变常数。
假设逆压电效应诱导产生的载荷作用在压电作动器中面的中心,对于图1所示结构,可将载荷等效为作用在压电片边界上的力和力矩,从而得到作动器输入电压与驱动载荷之间的关系为
F=DE1
(3)
式中:D为压电作动器的力电转换矩阵,其表达式为
根据有限元方法,可建立带有p个压电作动器薄板结构的动力学方程,其表达式为
(4)
式中:x为节点位移向量;M、C和K分别为质量、阻尼和刚度矩阵;fi(t)为第i个作动器的等效载荷向量;Di为离散后第i个作动器的力电转换矩阵。引入模态振型矩阵Φ,并令x(t)=Φη(t),η(t)为n×1维的模态坐标向量,将模型动力学方程转换到模态坐标系,得到
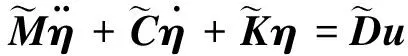
(5)
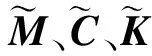
其中:ωi和ζi(i=1,2,…,n)分别为第i阶模态频率和模态阻尼比。定义2n×1维的状态向量
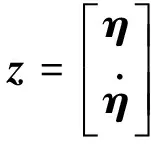
(6)
式(5)可以改写为
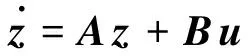
(7)
式中:
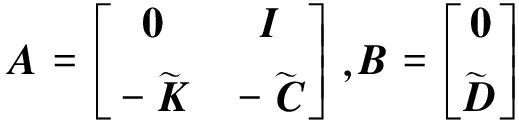
(8)
从上面的推导可以看出,作动器布局直接影响到系统的输入矩阵B,进而影响系统的可控性。
2 模态可控性与模态价值理论
可控性是系统输入对系统状态控制性能的描述,这里使用系统可控性描述多组作动器对压电结构的控制性能,由此建立多作动器的布局优化模型。根据Popov、Belevitch和Hautus(PBH)提出的系统可控性判据[19],如果系统的第i阶模态可控,则矩阵B的任意列向量不与矩阵A的第i个左特征向量正交。PBH判据虽然能够判断系统的可控性,但只能定性描述系统能否控制,不能对系统的控制性能做出准确的描述,为此Hamdan和Nayfeh[14]通过PBH判据的几何学解释,提出模态可控性指标,使用系统矩阵A的左特征向量和输入矩阵B的列向量之间的夹角,来定量描述作动器对系统第i阶模态的控制性能,第j个作动器对系统第i阶模态的控制性能为
(9)
式中:qi为矩阵A的左特征向量;bj为矩阵B的第j列。由式(9)可知,当θij=0°时,第j个作动器对系统第i阶模态可控性最大。当θij=90°时,第j个作动器对系统第i阶模态不可控。所有作动器对第i阶模态的可控性βi可表示为
(10)
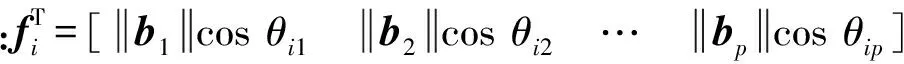
使用模态可控性来判断系统的可控性时,通常是以最小的模态可控性βi作为系统可控性的指标。但在实际应用中,直接使用该准则存在一定的局限性,例如,对于线性系统,假设系统第k阶模态可控性βk最小,系统的优化目标是使得βk最大。但是如果系统第k阶模态在系统的实际输出中并不占主导因素地位,这时使βk最大作为可控性指标就不再合适。将模态可控性和模态价值分析方法[20]结合起来,就可以解决这一问题。
模态价值可以定义为系统在特定的扰动下,各阶模态对系统输出的贡献。它可以用来表示特定输入下系统各阶模态对输出影响的重要性[21]。

(11)
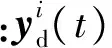
(12)
引入模态坐标转换矩阵Φ,有
(13)
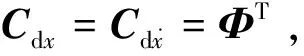
这时V表示系统的动能与势能之和。
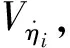
(14)
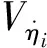
(15)
式中:
其中:[·]ij为矩阵·的第i行第j列元素。模态价值Vi表示第i阶模态对总模态价值V的贡献。在此使用模态价值比Vi/V来表示系统在特定扰动下各阶模态对系统性能的贡献。
3 优化指标
优化指标是对作动器布局好坏的评价依据,通过前述模态可控性原理,建立作动器布局和模态可控性的关系,模态价值分析给出了系统各阶模态对系统实际输出的影响。Junkins和Kim[15]提出如下可控性指标:
(16)
Aldraihem等[22]认为总的模态可控性βi总是大于零,因此取如下优化指标:
(17)
上述优化指标保证了作动器传递给系统的能量最大,使得对n阶模态的总控制性能最大,但不能确保每阶模态的控制性能,甚至造成某些模态不可控。因此,本文提出如式(18)所示的优化指标。
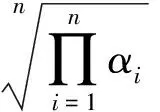
(18)
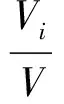
连续系统具有无限自由度,在实际分析时通常使用有限自由度系统来近似描述。在对振动进行主动控制时,这种简化会因截断的剩余模态造成系统的控制溢出问题[23]。这可以通过优化作动器的位置,使得剩余模态的输出可控性最小来解决,但同时又会造成系统控制性能的损失,因此需要在这两者之间做出权衡。
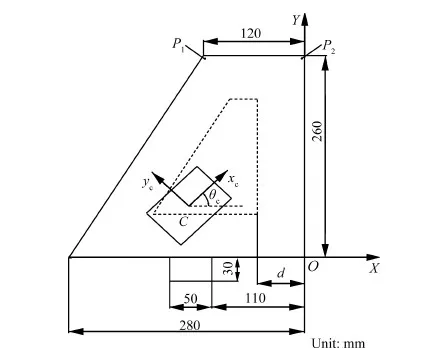
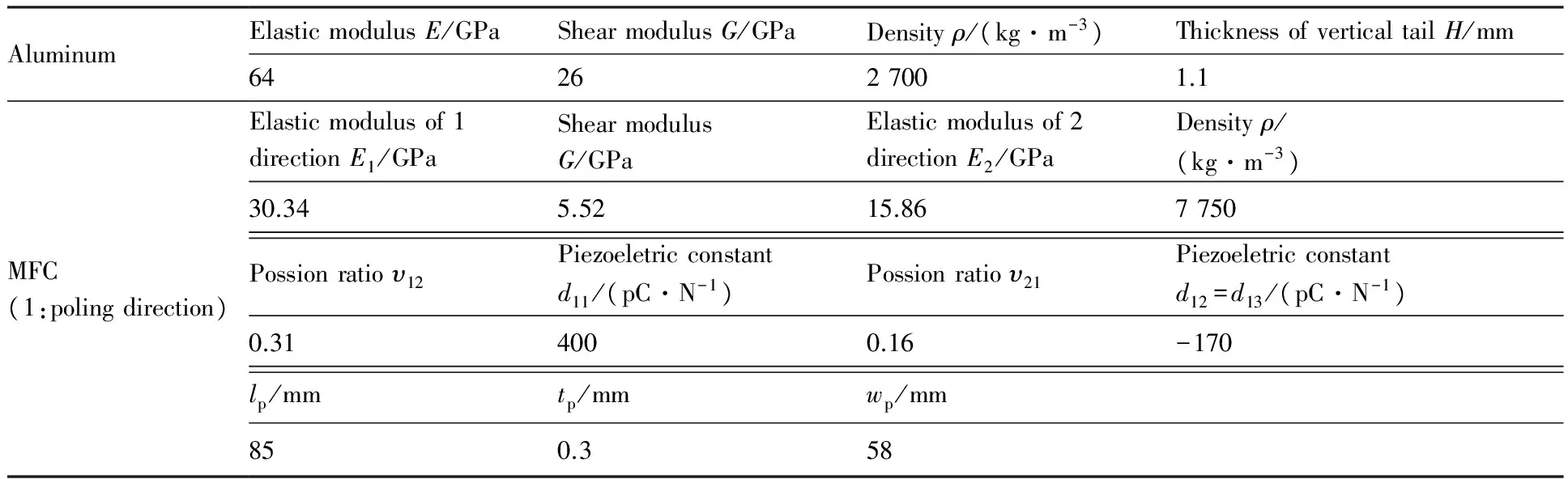
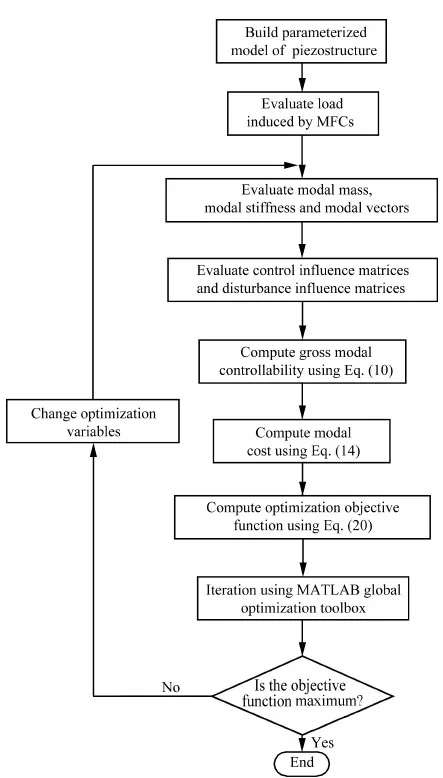
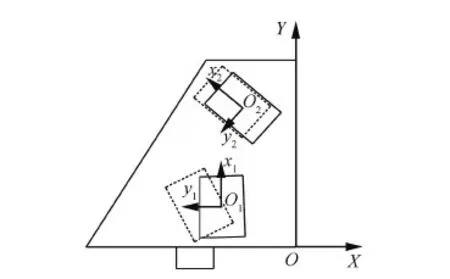
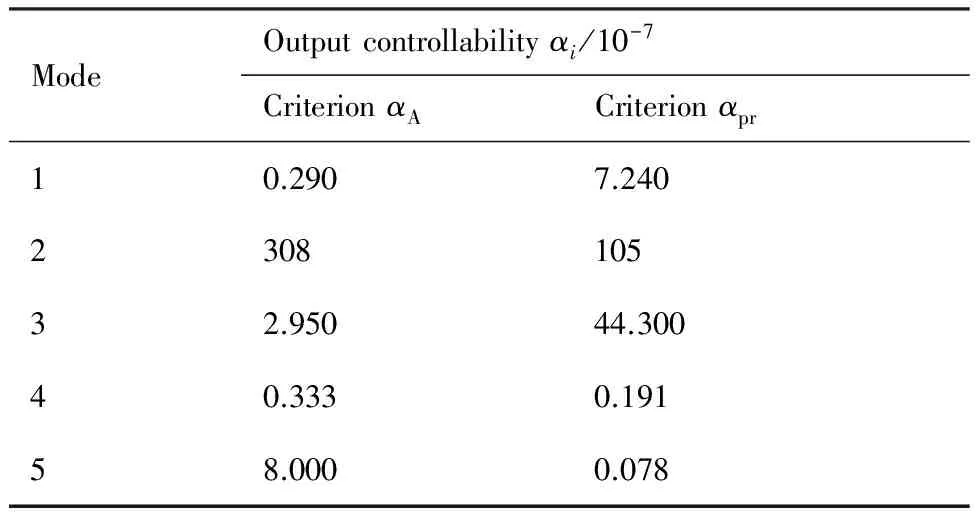
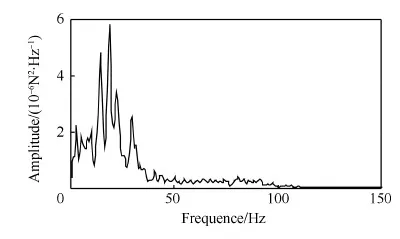
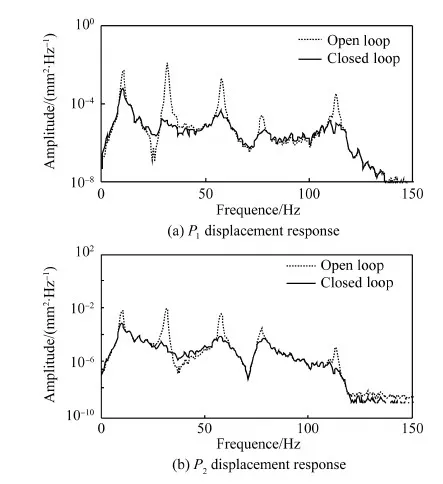
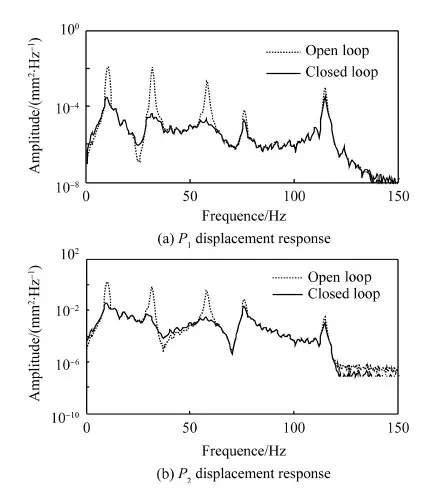
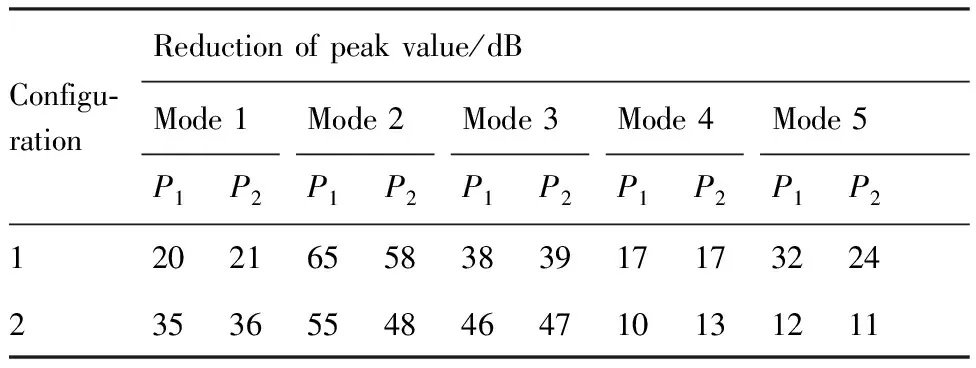
对于N阶振动系统,对前n阶模态进行控制(n (19) 式中:权值γ可用来调节控制模态和剩余模态之间的输出可控性。在实际应用中可以通过计算作动器在初始优化位置时,系统的输出可控性αi,选取权值使得式(19)右端第1项与第2项的数值在同一量级来确定γ,并且γ越大最终优化结果的剩余模态的输出可控性越小,而式(18)可以看做式(19)在γ=0时的特例。 4.1 MFC作动器布局优化 图2 垂尾模型Fig.2 Vertical tail model 计算粘贴MFC前后结构的固有频率,结果如表2所示,表中未粘贴MFC结构的固有频率和模态阻尼比为试验测试所得。 相对于传统的优化算法,遗传算法具有良好的全局搜索能力并能够解决复杂的目标函数和约束条件下的优化问题。不少学者已经将遗传算法用于作动器和传感器位置的优化,并得到了理想的优化结果[10-13,16-17]。 表1 垂尾模型与MFC的材料属性Table 1 Material properties of vertical tail model and MFC 表2模型前5阶固有频率和阻尼比 Table2Thefirstfivenaturalfrequenciesanddampingratios ModeNaturalfrequency(withoutMFC)/HzNaturalfrequency(with2MFCs)/HzDampingratio/%110.2810.230.35230.2231.750.18356.4558.140.24475.2776.360.145110.11115.050.17 (20) 式中:约束条件(a)为压电作动器布局角度约束;约束条件(b)~(e)为压电作动器形心的位置约束;约束条件(f)为两个压电作动器之间的约束。具体的优化计算流程如图3所示。在优化时通过每次迭代过程中的有限元网格更新,保证压电作动器形心位置的连续优化,并使用MATLAB全局优化工具箱下的遗传算法,计算得到全局最优解。 作为对比,使用Aldraihem等[22]提出的式(17)为目标函数,优化得到优化布局1,两片MFC的位置分别为(117°。128.6,57.6)和(139°,85.2,202.0),具体布局如图4虚线所示。使用本文提出的目标函数式(20)计算得到优化布局2,两片MFC的位置分别为(92°,98.7,56.2)和(137°,71.2,193.4),具体布局如图4实线所示。两种优化结果的模态输出可控性列于表3中,可以看出,Aldraihem的目标函数会造成第2阶输出可控性过大,第1、3阶模态输出可控性偏小;而本文提出的目标函数的优化结果显著提高了第1、3阶模态的输出可控性,并且考虑控制溢出后,第4、5阶剩余模态的输出可控性显著减低。 图3 优化流程图Fig.3 Flowchart of optimization process 图4 作动器优化布局方案Fig.4 Optimal configuration of actuators 表3 输出可控性对比Table 3 Comparison of output controllability ModeOutputcontrollabilityαi/10-7CriterionαACriterionαpr10.2907.240230810532.95044.30040.3330.19158.0000.078 4.2 垂尾抖振响应控制 为了验证本文提出的优化指标计算所得作动器布局能有效控制垂尾的抖振响应,使用LQG最优控制方法来控制垂尾在抖振载荷激励下的振动响应。如图2所示,选择垂尾梢部前、后缘的P1和P2两点的位移响应作为反馈信号。 LQG控制最优指标为 (21) 式中:权矩阵Q为对称的半正定矩阵,R为对称正定矩阵,权值Q反映系统的输出误差,R反映系统的输入能量,通常Q越大控制器性能越好,R越大控制器能量消耗越小(控制电压越小),因此权衡控制性能与控制电压可以选择合适的Q与R,计算得到LQG控制器参数。 图5所示为抖振载荷的功率谱密度(PSD)。载荷PSD峰值分布在0~40 Hz频带内,该抖振载荷能够有效激励出垂尾结构的前3阶模态,因此选取系统前3阶为控制模态,同时考虑到在实际应用中,控制系统回路不可避免地存在高频噪声,有可能因控制激发起第4、5阶模态的高频振动,为此选取第4、5阶模态为剩余模态来防止系统的控制溢出。 使用同一控制器,分别针对图4中的两种布局方案进行控制仿真,对比开环和闭环系统反馈点P1和P2处位移响应,如图6和图7所示,计算控制前后P1和P2处0~70 Hz带宽位移响应的均方根(RMS)值可知:采用布局1,响应分别降低92%和89%。而采用布局2,响应可分别降低96%和94%。每阶模态的峰值降低值如表4所示。 图5 垂尾根部抖振载荷功率谱密度(PSD)Fig.5 Power spectral density (PSD) of buffet loads on root of vertical tail 图6 位移响应PSD(布局1)Fig.6 PSDs of displacement response (Configuration 1) 从控制结果的对比可以看出,两种布局方案均能降低垂尾的前3阶抖振响应,布局1的第2阶模态控制最好,可使两反馈点响应峰值分别降低65 dB和58 dB,第1、3阶模态控制较差,反馈点P1的第4、5阶剩余模态的响应峰值分别降低了17 dB和32 dB,反馈点P2的第4、5阶剩余模态的响应峰值分别降低了17 dB和24 dB,由于在抖振控制中更关心低阶模态振动的控制效果,因此布局1不能有效利用系统的控制能量;使用本文提出的目标函数进行优化得到的布局2,能够改善控制能量的利用,其反馈点P1的第1、3阶模态的响应峰值分别降低了35 dB和46 dB, 反馈点P2的第1、3阶模态的响应峰值分别降低了36 dB和47 dB,并且反馈点P1的第4、5阶剩余模态的响应峰值只降低了10 dB和12 dB,反馈点P2的第4、5阶剩余模态的响应峰值只降低了13 dB 和11 dB,布局2能够有效地将控制能量集中到前3阶模态的控制上,提高了垂尾抖振控制效果,降低了剩余模态的控制能量,降低了控制溢出风险,控制仿真结果验证了4.1节得到的输出可控性对比结果。 图7 位移响应PSD(布局2)Fig.7 PSDs of displacement response (Configuration 2) 表4 控制结果对比Table 4 Comparison of response control Configu⁃rationReductionofpeakvalue/dBMode1Mode2Mode3Mode4Mode5P1P2P1P2P1P2P1P2P1P2120216558383917173224235365548464710131211 1) 本文提出的压电作动器连续布局优化方法所得布局方案能够有效控制垂尾抖振响应。 2) 本文提出的压电作动器连续布局优化方法能提高抖振开环控制系统控制模态的输出可控性,使控制能量集中在所关心的抖振控制模态,提高了抖振响应的控制效果。 3) 本文提出的压电作动器连续布局优化方法,能降低抖振开环控制系统剩余模态的输出可控性,降低系统对剩余模态的能量输入,从而降低了系统控制溢出的风险。 [1] LEE B H K. Vertical tail buffeting of [2] MOSES R W, WIESEMAN C D, BENT A A, et al. Evaluation of new actuators in a buffet loads environment[C]//Proceedings of SPIE. Bellingham,WA: The International Society for Optics and Photonics, SPIE, 2001, 4332: 10-21. [3] CHEN Y, ULKER F D, WICKRAMASINGHE V, et al. Development of robust control law for active buffeting load alleviation of smart fin structures[J]. Journal of Intelligent Material Systems and Structures, 2014, 25(7): 818-831. [4] CHEN Y, VIRESH W, ZIMCIK D. Development and verification of real-time controllers for F/A-18 vertical fin buffet load alleviation[C]//Proceedings of SPIE. Bellingham,WA: The International Society for Optical Engineering, SPIE, 2006: 617310.1-617310.12. [5] GUPTA V, SHARMA M, THAKUR N. Optimization criteria for optimal placement of piezoelectric sensors and actuators on a smart structure: A technical review[J]. Journal of Intelligent Material Systems and Structures, 2010, 21(12): 1227-1243. [6] ARBEL A. Controllability measures and actuator placement in oscillatory systems[J]. International Journal of Control, 1981, 33(3): 565-574. [7] HAC A, LIU L. Sensor and actuator location in motion control of flexible structures[J]. Journal of Sound and Vibration, 1993, 167(2): 239-261. [8] COLLET M. Shape optimization of piezoelectric sensors dealing with spill-over instability[J]. IEEE Transactions on Control Systems Technology, 2001, 9(4): 654-662. [9] BRUANT I, PROSLIER L. Optimal location of actuators and sensors in active vibration control[J]. Journal of Intelligent Material Systems and Structures, 2005, 16(3): 197-206 [10] BRUANT I, GALLIMARD L, NIKOUKAR S. Optimal piezoelectric actuator and sensor location for active vibration control, using genetic algorithm[J]. Journal of Sound and Vibration, 2010, 329(10): 1615-1635. [11] 王军, 杨亚东, 张家应, 等. 面向结构振动控制的压电作动器优化配置研究[J]. 航空学报, 2012, 33(3): 494-500. WANG J, YANG Y D, ZHANG J Y, et al. Investigation of piezoelectric actuator optimal configuration for structural vibration control[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(3): 494-500 (in Chinese). [12] SADRI A M, WYNNE R J, WRIGHT J R. Robust strategies for active vibration control of strain actuated plate like structures[C]//UKACC International Conference on (Conf. Publ. No. 455) Control ’98. Herts, London: IET, 1998: 213-218. [13] SADRI A M, WRIGHT J R, WYNNE R J. Modelling and optimal placement of piezoelectric actuators in isotropic plates using genetic algorithms[J]. Smart Materials and Structures, 1999, 8(4): 490-498. [14] HAMDAN A M A, NAYFEH A H. Measures of modal controllability and observability for first-and second-order linear systems[J]. Journal of Guidance, Control, and Dynamics, 1989, 12(3): 421-428. [15] JUNKINS J L, KIM Y. Measure of controllability for actuator placement[J]. Journal of Guidance, Control, and Dynamics, 1991, 14(5): 895-902. [16] MEHRABIAN A R, YOUSEFI-KOMA A. A novel technique for optimal placement of piezoelectric actuators on smart structures[J]. Journal of the Franklin Institute, 2011, 348(1): 12-23. [17] SOHN J W, CHOI S B, KIM H S. Vibration control of smart hull structure with optimally placed piezoelectric composite actuators[J]. International Journal of Mechanical Sciences, 2011, 53(8): 647-659. [18] 李敏, 陈伟民, 王明春, 等. 压电驱动的载荷比拟方法[J]. 中国科学E辑: 科学技术, 2009, 39(11): 2576-2584. LI M, CHEN W M, WANG M C, et al. A load simulation method of piezoelectric actuator in FEM for smart structure[J]. Science in China Series E: Technological Science, 2009, 39(11): 2576-2584 (in Chinese). [19] POPOV V M. Hyperstability of control systems[M]. Berlin: Springer-Verlag, 1974: 52-55. [20] SKELTON R E, SINGH R, RAMAKRISHNAN J. Component model reduction by component cost analysis[C]//AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 1988. [21] JUNKINS J L, KIM Y. Introduction to dynamics and control of flexible structures[M]. Reston: AIAA, 1993: 316-327. [22] ALDRAIHEM O J, SINGH T, WETHERHOLD R C. Optimal size and location of piezoelectric actuator/sensors: Practical considerations[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(3): 509-515. [23] PREUMONT A. Vibration control of active structures: An introduction[M]. 3rd ed. Berlin: Springer, 2011: 261-264. 梁力男,硕士研究生。主要研究方向:结构振动主动控制。 Tel.: 029-88460461 E-mail: lil1991.0@163.com 杨智春男,博士,教授,博士生导师。主要研究方向:气动弹性力学、 结构动力学及结构健康监测。 Tel.: 029-88460461 E-mail: yangzc@nwpu.edu.cn URL:www.cnki.net/kcms/detail/11.1929.V.20160122.1408.002.html Optimizationofpiezoelectricactuatorconfigurationonaverticaltailforbuffetingcontrol LIANGLi,YANGZhichun*,OUYANGYan,WANGWei InstituteofStructuralDynamicsandControl,SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China Inordertoimprovethecontrolperformanceofthetailbuffetcontrolsystemusingpiezoelectricactuators,anewoptimizationcriterionisusedtooptimizetheconfigurationofpiezoelectricactuatorsbasedonoutputcontrollability.Macro-fibercomposite(MFC)piezoelectricactuatorismodeledbyaloadsimulationmethodofpiezoelectricactuator.DynamicequationsoftheverticaltailincorporatingMFCactuatorsareobtainedbyfiniteelementmethod.Anobjectivefunction,usingmodalcontrollabilityandmodalcosttheory,issuggestedwiththeconsiderationofresidualmodestolimitthespillovereffect.Inordertocontrolthefirstfivemodesoftheverticaltail,geneticalgorithmisusedtofindtheoptimalconfigurationandlinear-quadraticGaussian(LQG)controllerisadoptedtocontroltheresponseoftheverticaltail.SimulationresultsshowthattheoptimalconfigurationofMFCactuatorsnotonlyimprovesthecontrolperformancebutalsobalancessystemcontrollabilityandreducestheinfluenceofresidualmodes. piezoelectricactuators;smartstructures;optimizationofconfiguration;buffeting;controllability 2015-09-18;Revised2015-11-22;Accepted2016-01-05;Publishedonline2016-01-221408 NationalNaturalScienceFoundationofChina(11502208) .Tel.:029-88460461E-mailyangzc@nwpu.edu.cn 2015-09-18;退修日期2015-11-22;录用日期2016-01-05; < class="emphasis_bold">网络出版时间 时间:2016-01-221408 www.cnki.net/kcms/detail/11.1929.V.20160122.1408.002.html 国家自然科学基金 (11502208) .Tel.:029-88460461E-mailyangzc@nwpu.edu.cn 梁力, 杨智春, 欧阳炎, 等.垂尾抖振主动控制的压电作动器布局优化J.航空学报,2016,37(10):3035-3043.LIANGL,YANGZC,OUYANGY,etal.OptimizationofpiezoelectricactuatorconfigurationonaverticaltailforbuffetingcontrolJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):3035-3043. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0005 V211.47; TB535 A 1000-6893(2016)10-3035-09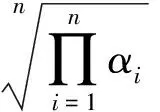
4 算例分析
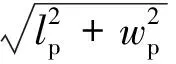

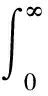
5 结 论
Fighter aircraft[J]. Progress in Aerospace Sciences, 2000, 36(3): 193-279.
