巧用“函数对比法”进行实验误差分析

姜庆荣 聂传虎

测电源电动势和内阻实验在高中阶段是高考的一个重点内容，而该实验的一个难点就是对实验的结论进行误差分析.误差分析的方法有很多，各种教辅材料中主流的误差分析法主要有三种：（1）解析法，（2）等效电源法，（3）图像法.下面先对这三种误差分析的方法做简单的说明.

一、几种常见的误差分析法

1.解析法

将实际数据所联立的方程组解得的电源电动势和内阻与真实值进行比较.

此法要求学生具有较好的解复杂的二元一次方程组的能力.数学功底较差的同学即使知道误差分析的原理，也可能无法完成对复杂二元一次方程的求解.

2.等效电源法

将电表和电源的组合看成是等效电源，再分析等效电源的电动势和内阻与真实电动势和内阻之间的关系，从而进行误差分析.该方法看上去比较简单，实际对学生的要求很高，其缺陷在于，学生在将电源与电压表并联时如何正确看待等效电源的断路电压以及并联等效内阻时存在较大的思维障碍.

3.图象法

先作出理论的U-I图象，然后根据实际的实验电路的误差来源，通过描点法作出实际的U-I图象，然后比较理论图与实际图之间的差别，由图象的截距和斜率来判断测量值和真实值之间的差异.这种方法比较直观，对于熟练掌握误差来源以及图象功底比较扎实的学生来讲，此法较为简单.但对于中等或以下水平的学生来讲，这种方法是比较难以理解的，而且用这种方法只能定性进行误差分析，至于误差是为多少的定量问题，这种方法就无法解决了.

二、函数对比法的应用

本文将对一种直接误差分析法进行研究，笔者称之为“函数对比法”.测电源电动势和内阻的基本实验方案有伏安法、伏阻法、安阻法等.每种方法都必须测出两个变量，然后根据闭合电路欧姆定律列出关于这两个变量的一次函数方程.所谓函数对比法，即：将考虑系统误差和不考虑系统误差的两个方程进行对照（主要是方程系数的对照），得到测量值和理论值之间的关系，从而对系统误差作更深入的定量研究.笔者就“测电源电动势和内阻”的实验的几种不同的实验方案，采用函数对比法进行误差分析研究.

1.实验方案1的误差分析

实验方案1（即伏安法的一种连接方式）的实验电路图如图1所示，理想情况下，闭合电路欧姆定律可写成

U=E-Ir（1）

其中U指路端电压，I指干路电流，若用不考虑系统误差的U、I组建方程组，解出的当然是真实的E和r.但是由于电流表分压，电压表测得的并不是真实的路端电压，可用U测表示，电流表读数用I测表示.根据闭合电路欧姆定律，考虑系统误差后的的方程应为

U测=E-I测（r+RA）（2）

将（2）式与（1）式进行对照，不难发现有U测、I测组建的方程组解得的值应为E测=E和r测=r+RA.所以采用这种连接方式所测出的电源电动势是正确的，而电源的内阻则测大了.

2.实验方案2的误差分析

若采用图2的连接方式（伏安法的另一种连接方式），我们不妨也来做个尝试.此时电压表测的是准确的路端电压，但由于电压表的分流，电流表测得的值小于真实的干路电流.则实际情况下闭合电路欧姆定律的表达式应为：

U测=E-（I测+U测RV）r（3）

U测=E-I测r-U测RVr（4）

U测（1+rRV）=E-I测r（5）

U测=RVRV+rE-I测（6）

将（6）式与（1）式进行对比，可知由U测、I测组建方程组所得的解应为E测=RVRV+rE和r测=rRVRV+r.所以采用此种连接方式测得的电动势偏小了，电源内阻也偏小了.

3.实验方案3的误差分析

实验方案3（伏阻法）电路图如图3所示.此法的闭合电路欧姆定律的表达式写成：

U=E-URr（7）

变形得1U=1E+rE·1R（8）

而实际实验测得的数据记为U测和R测，考虑系统误差后的闭合电路欧姆定律表达式应写成

U测=E-（U测RV+U测R测）r（9）

变形得U测[1+（1RV+1R测）r]=E（10）

将（10）式两边取倒数，再变形有

1U测=1E[1+（1RV+1R测）r]（11）

现在的目的是将（11）式变化成（8）式的形式，从而更好地与（8）式进行对照.

1U测=1E（RV+rRV）+rE·1R测（12）

将（12）式再变形得

1U测=1ERVRV+r+rRVRV+rERVRV+r·1R测（13）

将（13）式与（8）式进行对比不难发现，用U测和R测得到的解应为

E测=ERVRV+r和r测=rRVRV+r.

所以采用实验方案3所测得电源电动势和内阻均偏小了.

4.实验方案4的误差分析

实验方案4（安阻法）电路图如图4所示.此法的闭合电路欧姆定律的表达式写成：

I=ER+r（14）

变形得1I=1ER+rE（15）

而实际实验测得的数据记为I测和R测，考虑系统误差后的闭合电路欧姆定律表达式应写成

I测=ER测+r+RA（16）

变形得1I测=1ER测+r+RAE（17）

将（17）式与（15）式进行对比不难发现，用I测和R测得到的解应为

E测=E，r测=r+RA.

所以采用实验方案4所测得电源电动势是准确的和内阻均偏大了.

三、“待定系数法”进行误差分析的拓展应用

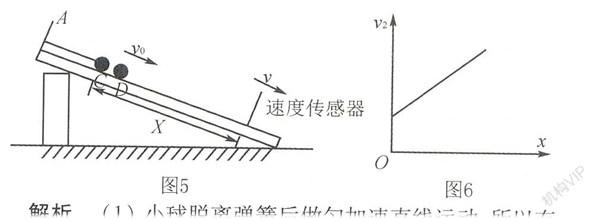
题目设计某实验小组设计了测小球运动初速度和加速度的实验，实验装置如图所示.一平直长木板，表面粗糙程度均匀，长木板末端固定一挡板A，将长木板末端垫起，并保持长木板与水平面的夹角恒定.一轻质软弹簧一端固定于挡板A，自然伸长时弹簧另一端能够达到D点.长木板B处装有速度传感器.现将一小球放在弹簧的前端并轻微压缩至C点，同时用细线穿过弹簧将小球和挡板A相连接，（CD距离足够短，可忽略不计），测出BC间的距离为x.现烧断细线，小球下滑时经过B点的速度由速度传感器测出，记为v，求：

（1）改变速度传感器所在的位置B点，重复几次上述步骤，可得到一组关于x和v的数据.现作出v2-x的图像，如图所示.直线的斜率为k，纵坐标轴的截距为b，则小球脱离弹簧瞬间的速度大小v0=，小球脱离弹簧后的加速度大小a=（结果用k、b表示）.

（2）若CD间距离不可忽略，但由于疏忽，测量时还是取BC之间的距离为x，从而可能给实验带来误差.若依然按（1）中的思想求v0和a，则测出的v0，a（选填“偏大”、“偏小”或“无误差”）.

解析（1）小球脱离弹簧后做匀加速直线运动，所以有

v2-v20=2ax得v2=2ax+v20（1）

结合图像可知k=2a，b=v20，

所以，a=k2，v0=b.

（2）假设CD间的距离为x′，CB间的距离用x测表示，小球到达B的速度用v测表示，考虑到实验误差，实际的方程应写成

v2测-v20=2a（x测- x′）

变形得v2测=2ax测+（v20-2ax′）（2）

将（2）式与（1）式进行对照可知，加速度的测量是准确的，初速度的测量偏小了.测得的具体值与真实之间的关系为：a测=a，v0测=-2ax′+v20.

“待定系数法”的方法总结：先根据实际实验电路图写出实际的方程，再将该方程和原始理论的方程进行系数的对照，从而得出测量值与真实值之间的关系.操作的关键在于如何将实际的方程转化成和理论方程类似的形式.这种方法相比于等效电源法和图象法来讲更为严谨，不仅可以得出测量结果偏大偏小的问题，还可以得到具体误差的大小，是一种比较常规的、易懂的误差分析法，此法建立在一定数学运算的基础上，学生在进行其他实验的误差分析时也可以采用类似地思想进行研究.