几何画板在中学数学教学中的实践及体会
2016-11-19徐娟
徐娟
随着科学技术的不断发展,计算机在中学数学教学中的应用不断受到重视和强化.通过计算机技术的使用,使得数学知识变得更加直观、形象,将复杂枯燥的数转变成生动形象的形.几何画板作为整合数学知识与信息技术的主要工具,具有灵活绘图、智能变换、动态演示等优势,为中学数学教学注入新鲜血液.由于几何画板制作简单、操作方便,已经逐渐成为广大中学教师的信息化教学首选.在本文中,我们将从中学数学教学实践的角度出发,探讨几何画板在教学中的应用.
一、灵活绘图,性质探析
概念是数学的基础,性质则是对概念的升华和应用.在中学数学中,函数、不等式、方程、几何图形等,涉及众多的数学概念,对应众多的数学性质.几何画板作为联系数与形的电子化桥梁,具有灵活绘图的特点,对数学概念的性质揭示起到重要作用.
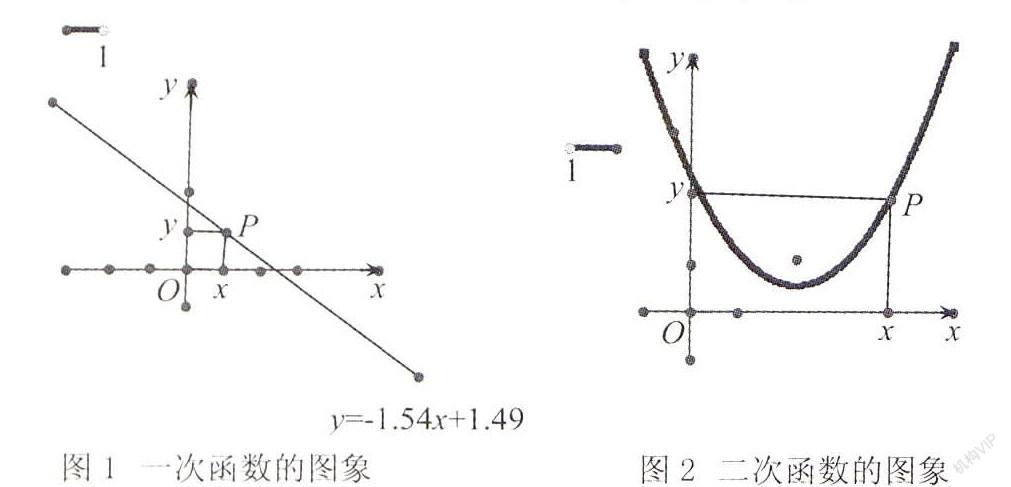
例如,在函数性质的教学中,我们往往是要求学生自行绘制坐标系,然后将给定的函数利用描点法进行图形绘制.然后通过对不同系数条件下函数图形的变化分析,得到对应的函数性质.但在几何画板的帮助下,这些程序我们都可以利用计算机进行,直接要求学生进行几何画板绘图,迅速揭示函数性质.对于一次函数的教学,学生们在坐标系内任意绘制一条直线,便可以迅速得到它的一元一次函数表达式.然后,要求学生尝试拖动、旋转直线,观察其系数值k、b的变化规律.如下图所示,我们拖动点P,发现其横纵坐标与系数的变化规律.于是,我们便可以直观地得到函数单调性.对于系数b,我们同样可以要求学生进行自主探究,利用几何画板寻找其性质规律.
对于二次函数,我们同样可以采取几何画板的性质探究模式.首先,通过几何画板可以迅速得到二次函数解析式及其图象.然后,通过拖动图形中的P点,可以发现二次函数的变化规律,找出其对称轴、单调区间等.通过转动图形,可以发现函数开口与解析式系数的关系.对于其余系数的变化规律探究,我们引导学生绘制对照性图形,迅速发现规律.对此,我们必须在备课时设置好几何画板的教学内容,从而有效掌控课堂教学节奏.
二、动态演示,训练思维
数与形是数学学科的两大基本内容,数形结合的思想贯穿于整个中学教学.几何画板能够有效地联系数与形,是一种重要的数学思想,对学生思维训练有着重要作用.对此,我们不妨利用数形结合与智能变换的方式,帮助学生掌握该思想,有效地构建数学模型.
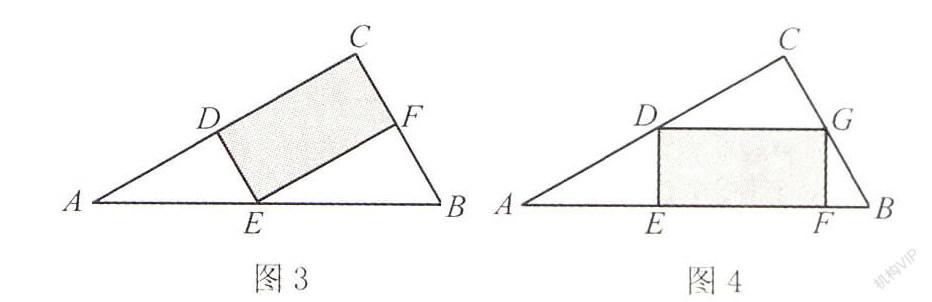
例题 有一张三角形纸片ABC,其中BC=6,∠C=90°,∠A=30°.
(1)如图3,若用这张纸片裁剪出一个矩形CDEF,使点D、E、F分别落在AC、AB、BC上,且使矩形CDEF的面积最大,则点E应选在何处?
(2)如图4,若用这张纸片裁剪出一个矩形DEFG,使点D、G分别落在AC、BC上,点E、F均在AB上,且使矩形DEFG的面积最大,则点E应选在何处?
三、智能变化,自主探究
在新课改背景下,数学教师对学生的自学能力要求不断提高,要求学生能够利用几何画板实现对数学知识的自主探究.几何画板的智能变换功能为学生的自主探究提供了可行性工具,同时也锻炼了学生的探究能力和实践操作能力,提高了数学课堂的教学效率.
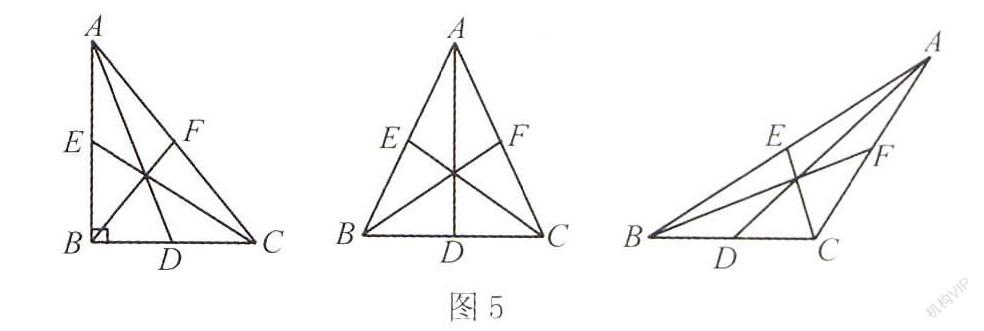
例如,在三角形中线定理的教学中,我为学生们提出了以下的自主探究课题,要求学生们利用几何画板的智能变换功能,对三角形中线交点位置进行探究.首先,学生们任意绘制了一个三角形,再利用几何画板绘制出它的三条中线,发现所有的中线都交于三角形内部一点.然后,学生们提出质疑:是否所有三角形的中线都交于图形内部一点呢?于是,他们通过拖动定点A,得到不同类型三角形的中线交点位置.显然,在锐角、直角、钝角三角形中,它们的中线都纷纷交于图形内部一点.此时,学生们便可以初步得到三角形中线都交于一点的性质.此时,学生们也实现了对三角形中线性质的自主探究.
总之,几何画板在中学数学教学中有着非常广泛和有效的运用,是数学知识与信息技术相结合的完美体现.虽说几何画板在中学数学教学中已经取得一定的效果,但其中还存在很多的不足之处,作为一线数学教师,我们还必须继续实践探索,为学生们总结出更加科学有效的几何画板教学模式.
