从小学生错误解决开放题说起

2016-11-19杨春雨

新课程·中旬 2016年4期

杨春雨

在“折扣”教学的练习课中，我设计了这样的一道练习题：甲乙两家商场卖同样的杯子，十一国庆期间，甲商场八折出售，乙商场买三送一，如果是你，你准备到哪家商场去买？

同学们完成得相当快，迫不及待地到展台前展示。甲商场：八折=80%，乙商场：3÷（1+3）×100%=75%，80%<75%，所以到乙商场去买。全班同学异口同声地说道：“对！”。只见“羽”十分激动地站起来，说道：“我觉得这样想似乎有问题，是不是应该考虑到要买多少个杯子呢？”教室里一下子炸开了锅，讨论的讨论，算的算。不一会，他理直气壮地走上讲台说：“假设买10个，甲：10×80%=8个，乙：10÷（1+3）=2组……2個，2×3+2=8个，那么到两个商场花的钱一样多；假设买8个，甲：8×80%=6.4个，乙：8÷（1+3）=2组，2×3=6个，那么到乙商场便宜些；假设买11个，甲：11×80%=8.8个，乙：11÷（1+3）=2组……3个，2×3+3=9个，到甲超市便宜些。”听完他的讲述后，有的同学鼓起了掌，有的同学显得很茫然，还有几个同学纷纷举起手来，俨然不服气：“杯子的个数怎么能是小数呢？你为什么要假设买10个、8个、11个杯子？假设其他的个数行么？”“买三送一不就是打七五折吗？让你这么一假设，买三送一可能等于七五折，大于七五折，也可能小于七五折？在什么情况下，买三送一就是七五折？我发现假设买11个杯子时，乙商场11÷（1+3）=2组……3个，剩下的这3个杯子还可以换一个杯子，就是说，他花了9个杯子的钱买了12个杯子……”

经过一番唇枪舌剑，同学们达成一致意见：打几折就是现价是原价的百分之几十，与个数没有关系，买三送一就与买的个数有关，当买的个数是（1+3）的倍数时，就相当于七五折，不是（1+3）的倍数时，就比七五折大。

这样的教学情境经常出现在我们的课堂中，像这样的开放性练习具有“条件不完备，条件多余需选择，条件不足需补充或答案不固定或具有多种解法，或有多种解题策略”的特点，所以学生在解决开放性习题时，也总是出现考虑不周全，知识点混淆，脱离实际解决问题等状况。面对如此情况，我们教师该如何去引导？下面我就结合教学谈谈自己在解决开放题时常用的几种策略。

一、动手操作，在实践中发现规律

动手操作活动能使抽象的知识形象化、具体化，有时我们只需给学生提供更多的动手操作的机会，让学生在实践和实验中感知，使他们不仅理解这些知识，而且能够灵活运用和拓展这些知识，形成完整的思维体系。

案例1：把一根绳子对折3次，相当于把这根绳子平均分成了几份？

对于这道题，学生不难理解“对折1次，就相当于把这根绳子平均分成2份”，但在理解“第二次对折时，就要把前两份的每一份都平均分成2份，就相当于把这根绳子平均分成4份……”有很大的难度。如果我们让学生实际动手操作，边操作，边记录，边思考，在实践中发现它的变化规律：对折n次，就相当于把这根绳子平均分成了份。

案例2：把一块长15dm，宽8dm的长方形铁皮，从四个角分别截去一个边长是2厘米的正方形，用剩余部分焊接成一个无盖的长方体水箱，这个水箱最多能盛水多少L？

教学时，我让一班的学生画图分析，二班的同学先动手做一做，再画图分析，课后作业反应，两个班的教学效果都很好。一周后，再次做类似的练习，二班的效果明显好于一班，这是为什么呢？事实证明：二班先通过动手操作感知，再上升到理论——画图分析、独立完成，思维经过了一次跳跃，对知识的理解更加深入。

二、联系生活实际，在生活中寻找原型

在教学中一方面要尽可能让抽象的数学概念在生活中找到原型，另一方面要创造条件，促使学生能用学到的数学知识去解决一些日常生活中有关的数学现象。

案例：小明家住6楼，每层楼大约高3米，当他站在客厅里时，距地面有多少米？

学生不假思索地认为是6×3=18（米），学生忽略了小明家住6楼，实际站在客厅里距地面只有5层楼的高度，这就是一个生活常识。像这样的常识性知识还有很多，比如：爬楼梯问题，水费、电话费，出租车费，如何购物更划算等问题，都与我们的生活息息相关，解题时，应联系生活，在生活中寻找原型，理解题意。

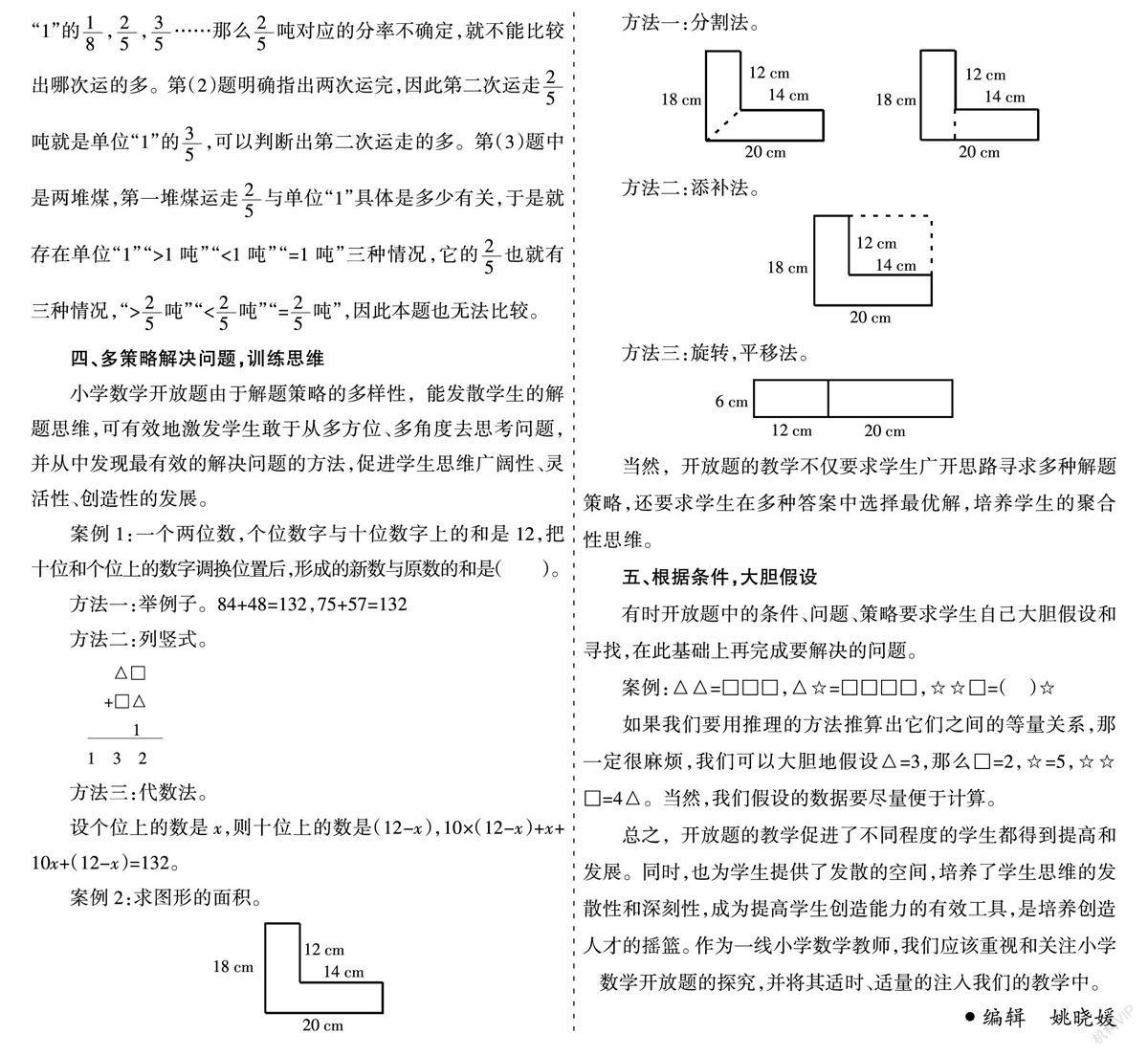
三、设计类比练习，找出异同，总结规律

学生认识水平的提高，很大部分得益于深刻的反思，于是在设计开放题时，可以通过设计形式、方法、内容等类比练习，引导学生抓联系，辨差异，巩固知识，丰富学生知识结构，深入反思，培养学生良好的学习习惯，激发学生思维的灵活性。

当然，开放题的教学不仅要求学生广开思路寻求多种解题策略，还要求学生在多种答案中选择最优解，培养学生的聚合性思维。

五、根据条件，大胆假设

有时开放题中的条件、问题、策略要求学生自己大胆假设和寻找，在此基础上再完成要解决的问题。

案例：△△=□□□，△☆=□□□□，☆☆□=（）☆