Vertex-distinguishing E-total Coloring of Complete Bipartite Graph K7,nwhen 7≤n≤95
2016-11-19CHENXIANGEN
CHEN XIANG-EN
(College of Mathematics and Statistics,Northwest Normal University,Lanzhou,730070)
Vertex-distinguishing E-total Coloring of Complete Bipartite Graph K7,nwhen 7≤n≤95
CHEN XIANG-EN
(College of Mathematics and Statistics,Northwest Normal University,Lanzhou,730070)
Let G be a simple graph.A total coloring f of G is called an E-total coloring if no two adjacent vertices of G receive the same color,and no edge of G receives the same color as one of its endpoints.For an E-total coloring f of a graph G and any vertex x of G,let C(x)denote the set of colors of vertex x and of the edges incident with x,we call C(x)the color set of x.If C(u)/=C(v)for any two different vertices u and v of V(G),then we say that f is a vertex-distinguishing E-total coloring of G or a VDET coloring of G for short.The minimum number of colors required for a VDET coloring of G is denoted by Xevt(G)and is called the VDET chromatic number of G.The VDET coloring of complete bipartite graph K7,n(7≤n≤95)is discussed in this paper and the VDET chromatic number of K7,n(7≤n≤95)has been obtained.
graph,complete bipartite graph,E-total coloring,vertex-distinguishing E-total coloring,vertex-distinguishing E-total chromatic number
2010 MR subject classification:O5C15
Document code:A
Article ID:1674-5647(2O16)O4-O359-16
1 Introduction and Notations
Graph theory is the historical foundation of the science of networks and the basis of information science.The problem in which we are interested is a particular case of the great variety of different ways of labeling a graph.
For an edge coloring(proper or not)g of G and a vertex x of G,let S(x)be the set(not multiset)of colors of the edges incident with x under g.
For a proper edge coloring,if S(u)/=S(v)for any two distinct vertices u and v,then the coloring is called a vertex-distinguishing proper edge coloring.The minimum number of colors required for a vertex-distinguishing proper edge coloring of G is denoted by X′s(G). This coloring is proposed in[1]and[2]independently.Many scholars have studied this parameter in[1]-[7].
For an edge coloring which is not necessarily proper,if S(u)/=S(v)for any two distinct vertices u and v,then the coloring is called a point distinguishing edge coloring.The minimum number of colors required for a point distinguishing edge coloring of G is denoted by X0(G).This coloring is proposed by Harary et al.[8]This parameter has been researched in many papers(see[9]-[14]).
For a total coloring(proper or not)f of G and a vertex x of G,let C(x)be the set(not multiset)of colors of vertex x and edges incident with x under f.
For a proper total coloring,if C(u)/=C(v)for any two distinct vertices u and v,then the coloring is called a vertex-distinguishing(proper)total coloring,or a VDT coloring of G for short.The minimum number of colors required for a VDT coloring of G is denoted by Xvt(G).
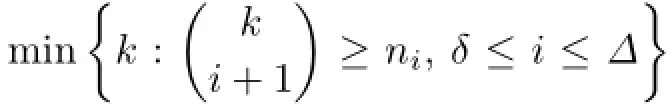
In the following we consider a kind of not necessarily proper total coloring which is vertex-distinguishing.A total coloring f of G is called an E-total coloring if no two adjacent vertices of G receive the same color,and no edge of G receives the same color as one of its endpoints.If f is an E-total coloring of graph G and for any u,v∈V(G),u/=v,we have C(u)/=C(v),then f is called a vertex-distinguishing E-total coloring,or a VDET coloring briefly.The minimum number of colors required for a VDET coloring of G is called the vertex-distinguishing E-total chromatic number of G and is denoted by Xevt(G).
The VDET colorings of complete graph,complete bipartite graph K2,n,star,wheel,fan,path and cycle were discussed by Chen et al.[18].A parameter was introduced in[18]:
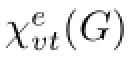
We have studied the vertex-distinguishing E-total colorings of mC3and mC4in[19]and confirmed Conjecture 1.1 for these two kinds of graphs.
In this paper,we consider the VDET coloring of complete bipartite graph K7,n(7≤n≤95)and confirm Conjecture 1.1 for K7,n(7≤n≤95).The results about the VDET coloring of complete bipartite graph K7,nwhen n≥96 are very long and published elsewhere.
For a vertex-distinguishing E-total coloring f of a graph G and an element z∈V(G)∪E(G),we use f(z)to denote the color of z under f.
Let X={u1,u2,u3,u4,u5,u6,u7},Y={v1,v2,v3,...,vn},V(K7,n)=X∪Y,E(K7,n)={uivj:1≤i≤7,1≤j≤n}.
Given a vertex-distinguishing E-total coloring f of K7,n,let
C(X)={C(u1),C(u2),...,C(u7)},C(Y)={C(v1),C(v2),...,C(vn)}.
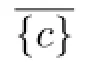
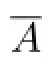
For other notations and terminologies,we may refer to[2O].
2 VDET Colorings of K7,7,K7,8
In Table 2.1,we have given a 5-VDET coloring of K7,8and we also obtain a 5-VDET coloring of K7,7if we delete the last line of Table 2.1.Note that the first line of Table 2.1 denotes the color sets of vertices from u1to u7;the second line of Table 2.1 denotes the colors of vertices from u1to u7;the third line of Table 2.1 denotes the color set of v1is{1,2,5},the color of v1is 1 and the colors of seven edges from u1v1to u7v1are 2,2,2,2,5,5,5,respectively;and so on;the ninth line of Table 2.1 denotes the color set of v7is{1,2,3,4},the color of v7is 1 and the colors of seven edges from u1v7to u7v7are 2,2,2,4,2,2,3,respectively.
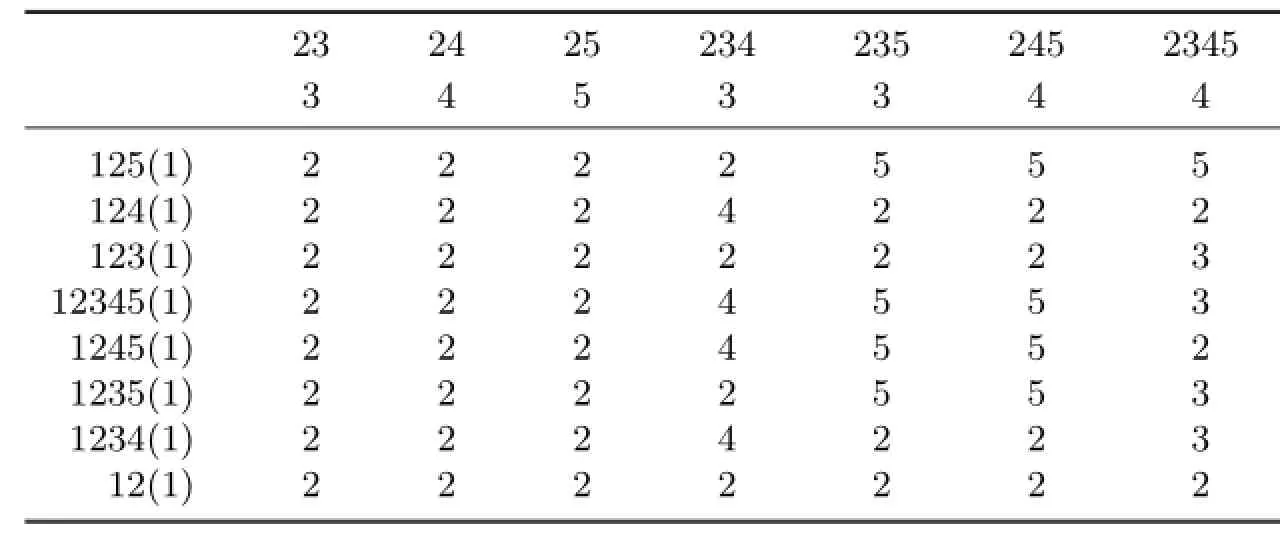
Table 2.15-VDET coloring of K7,8
Obviously,K7,7and K7,8does not have a 4-VDET coloring since each color set contains at least 2 colors under a VDET coloring of a complete bipartite graph and{1,2,3,4}has exactly 11 subsets which contain at least 2 elements.
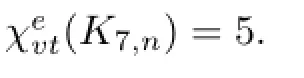
3 Several Lemmas
Lemma 3.1Let g be an l-VDET coloring of K7,n.Suppose that there are two distinct colors among g(u1),g(u2),...,g(u7),and g(ui)∈{1,2},i=1,2,...,7.If there exists a color a∈{3,4,...,l}such that{1,2,a}∈C(Y),i.e.,{1,2,a}is a color set of some vertex in Y,then{1,2}⊆C(ui),i=1,2,...,7.
Proof.Suppose that C(vjo)={1,2,a}.Then g(vjo)=a and the color of uivjois 2 if the color of uiis 1 and the color of uivjois 1 if the color of uiis 2.So{1,2}⊆C(ui),i=1,2,...,7.
Lemma 3.2Let g be an l-VDET coloring of K7,n.Suppose that there are two distinct colors among g(u1),g(u2),...,g(u7),and g(ui)∈{1,2},i=1,2,...,7.Let a1,a2,...,arbe r(≥2)distinct colors in{3,4,...,l}.If each 2-subset of{a1,a2,...,ar}is a color set of a vertex in Y,then there exist r-1 distinct colors in{a1,a2,...,ar}such that these r-1 distinct colors are contained in each set C(ui),i=1,2,...,7.
Proof.Since{a1,a2}belongs to C(Y),without loss of generality,we may assume that C(v1)={a1,a2}and g(v1)=a2.Then color a1is contained in each C(ui).
Since{a2,a3}belongs to C(Y),without loss of generality,we may assume that C(v2)={a2,a3}and g(v2)=a3.Then color a2is contained in each C(ui).
This process may proceed until that a1,a2,...,ar-2are contained in each C(ui). We consider the color set{ar-1,ar}of a vertex in Y,say C(vr-1)={ar-1,ar}and g(vr-1)=ar.Then color ar-1is contained in each C(ui).The conclusion is valid.
Lemma 3.3Let g be an l-VDET coloring of K7,n.Suppose that there are two distinct colors among g(u1),g(u2),...,g(u7),and g(ui)∈{1,2},i=1,2,...,7.Let a1,a2,...,arbe r distinct colors in{3,4,...,l}.
(i)If{1,a1,a2},{2,a1,a2}∈C(Y),then each color set in C(X)contains a1or a2,i.e.,a1∈C(ui)or a2∈C(ui),i=1,2,...,7;
(ii)For given j∈{1,2},if every 3-subset of{j,a1,a2,...,ar}which contains color j belongs to C(Y),then there exist r-1 distinct colors in{a1,a2,...,ar}such that these r-1 distinct colors are contained in each set C(ui)with g(ui)=j;
(iii)If every 3-subset of{1,2,a1,a2,...,ar}which contains color 1 or 2 but not both belongs to C(Y),then each set C(ui)contains at least r-1 colors in{a1,a2,...,ar},i=1,2,...,7.
Proof.(i)is obviously right.(ii)may be proved similar to the proof of Lemma 3.2.(iii)may be derived directly from(ii).
Lemma 3.4Let g be an l-VDET coloring of K7,n.Suppose that there are three distinct colors among g(u1),g(u2),...,g(u7),and g(ui)∈{1,2,3},i=1,2,...,7.
(i)If a,b∈{1,2,3},a/=b,and there exists one color c∈{4,5,...,l}such that{a,b,c}is a color set of some vertex in Y,then the color set of vertex x in X contains both a and b once the color of x is a or b;
(ii)If there exist colors c1,c2,c3∈{4,5,...,l}such that{1,2,c1},{1,3,c2},{2,3,c3}are the color sets of vertices in Y,then{1,2,3}⊆C(ui),i=1,2,...,7.
Proof.(i)Suppose C(vjo)={a,b,c}.Then g(vjo)=c,and the color of each edge uivjois b or a.If g(ui)=a,then g(uivjo)=b;if g(ui)=b,then g(uivjo)=a.The conclusion follows.
(ii)By(i),we know that the color set of vertex x in X contains 2,3 if the color of x is 1;the color set of vertex x in X contains 1,3 if the color of x is 2;the color set of vertex x in X contains 1,2 if the color of x is 3,then(ii)follows.
Similar to Lemma 3.4,we have the following Lemma 3.5.
Lemma 3.5Let g be an l-VDET coloring of K7,n.Suppose that there are four distinct colors among g(u1),g(u2),...,g(u7),and g(ui)∈{1,2,3,4},i=1,2,...,7.
(i)If a,b∈{1,2,3,4},a/=b,and there exists one color c∈{5,6,...,l}such that{a,b,c}is a color set of some vertex in Y,then the color set of color a vertex in X contains b,and the color set of color b vertex in X contains a;
(ii)If there exist colors c1,c2,c3,c4,c5,c6∈{5,6,...,l}such that{1,2,c1},{1,3,c2},{1,4,c3},{2,3,c4},{2,4,c5},{3,4,c6}are the color sets of vertices in Y,then{1,2,3,4}⊆C(ui),i=1,2,...,7.
4 Main Results
Proof.Assume that K7,nhas a 5-VDET coloring g.There are four cases to consider.
Case 1 u1,u2,...,u7receive the same color under g.
We may suppose that g(ui)=1,i=1,2,...,7,so every C(vj)does not include color 1. Suppose
Case 2 u1,u2,...,u7receive two different colors under g.
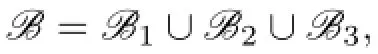

(1)Each C(ui)contains at least 3 colors.
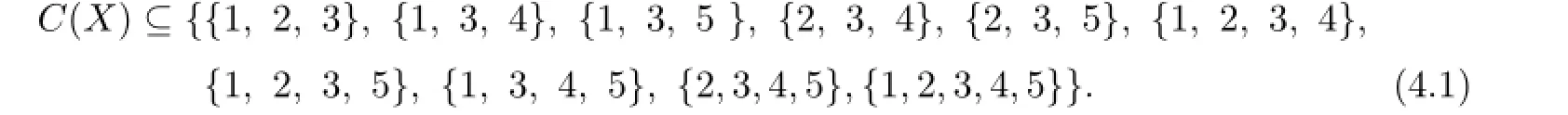
It implies that at least 5 sets among{3,5},{4,5},{1,2,4},{1,2,5},{1,4,5},{2,4,5},{3,4,5},{1,2,4,5}are the color sets of the vertices in Y.If{1,2,4}or{1,2,5}is in C(Y),then,by Lemma 1,we have{1,2}⊆C(ui),i=1,2,...,7.So
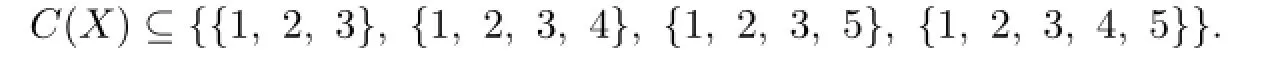
This is a contradiction.
If{4,5}is a color set of some vertex vjoand we may assume g(vjo)=5,then 4∈C(ui),i=1,2,...,7.But the right of(4.1)has 6 subsets which contain color 4,this is a contradiction.If{1,2,4},{1,2,5}and{4,5}are not in C(Y),then{3,5},{1,4,5},{2,4,5},{3,4,5},{1,2,4,5}∈C(Y).By Lemma 3.3,from{1,4,5},{2,4,5}∈C(Y),we know that each C(ui)contains 4 or 5 and{1,2,3}/∈C(X).Then{1,2,3}∈C(Y)and{1,2}⊆C(ui),i=1,2,...,7.Thus C(X)⊆{{1,2,3,4},{1,2,3,5},{1,2,3,4,5}}. This is a contradiction.
(2){1,2}is a color set of some vertex uio.
We suppose 9≤n≤11 in the following.
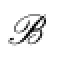
We suppose 9≤n≤13 in the following.
If{1,2,3}∈C(Y),then by Lemma 3.1 we have{1,2}⊆C(ui),i=1,2,...,7.But C(uio)={1,3}.This is a contradiction.
If{1,2,3},{3,4}and{3,5}are not in C(Y),then
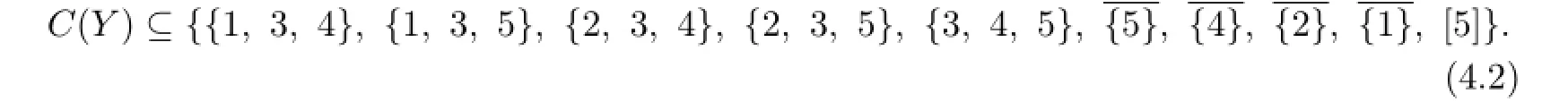
Thus 9≤n≤1O.When n=1O,(4.2)becomes an equality.From{1,3,4},{2,3,4}are in C(Y),by Lemma 3.3,we know that each C(ui)contain 3 or 4,and{1,5},{2,5},{1,2,5}are not in C(X).From{1,3,5},{2,3,5}are in C(Y)we know that each C(ui)contain 3 or 5,and{1,4},{2,4},{1,2,4}are not in C(X).Thus C(X)⊆{{1,3},{2,3},{1,2,3},{1,4,5},{2,4,5},{1,2,4,5}}.This is a contradiction. Suppose n=9 in the following.Exactly one member A in the right side of(2)is not in C(Y).
1)A/∈{{1,3,4},{1,3,5},{2,3,4},{2,3,5}}.
From{1,3,4},{1,3,5},{2,3,4},{2,3,5}∈C(Y),by Lemma 3.3,we know that each C(ui)contain 3 or 4,each C(ui)contain 3 or 5,{1,5},{2,5},{1,2,5},{1,4},{2,4},{1,2,4}are not in C(X).Thus
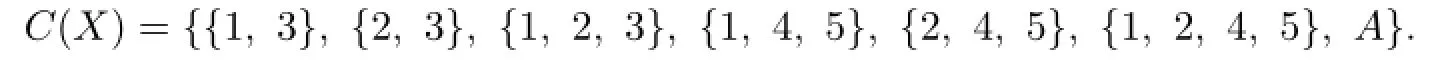
Without loss of generality,we assume C(v1)={1,3,4},C(u1)={1,3},C(u4)={1,4,5}. Then g(u1)=1=g(u4),g(u1v1)=3,g(v1)=4,g(u4v1)/=g(v1)=4.From g(u4v1)∈C(v1)={1,3,4},we know that g(u4v1)=1 or 3.This is a contradiction to g(u4)=1 or 3/∈C(u4).
2)A∈{{1,3,4},{2,3,4}}.
From{1,3,5},{2,3,5}∈C(Y),we know that each C(ui)contain 3 or 5,{1,4},{2,4},{1,2,4}are not in C(X).From{1,2,3,4}∈C(Y),we know that{1,5},{2,5}are not in C(X).Thus
C(X)⊆{{1,3},{2,3},{1,2,5},{1,2,3},{1,4,5},{2,4,5},{1,2,4,5},A}. One of{1,4,5}and{2,4,5}is the color set of a vertex in X.If C(u1)={1,4,5}and C(v1)={2,3,5},then g(u1)=1,g(u1v1)=5,g(v1)=3.It illustrates that the colors of all edges incident with v1are 2 or 5,and each C(ui)contains 2 or 5.This is a contradiction to C(uio)={1,3}.If C(u2)={2,4,5}and C(v1)={2,3,5},then g(u2)=2,g(u2v1)=5,g(v1)=3.It illustrates that the colors of all edges incident with v1are 2 or 5,and each C(ui)contains 2 or 5.This is a contradiction to C(uio)={1,3}.
3)A∈{{1,3,5},{2,3,5}}.
We have
C(X)⊆{{1,3},{2,3},{1,2,4},{1,2,3},{1,4,5},{2,4,5},{1,2,4,5},A}. One of{1,4,5}and{2,4,5}is the color set of a vertex in X.By comparing with C(v2)={2,3,4},we can know that each C(ui)contains 2 or 4.This is a contradiction to C(uio)={1,3}.
Case 3 There are exactly 3 distinct colors in g(u1),g(u2),...,g(u7).
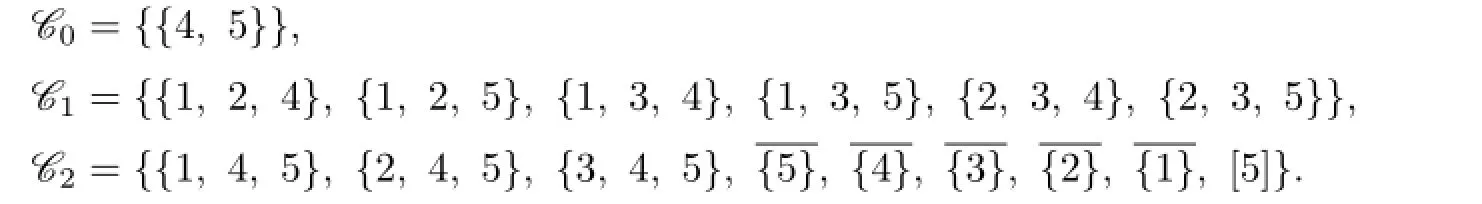
We suppose that 9≤n≤16 in the following.
Claim 1Either{1,4},{2,4},{3,4}are not in C(X),or{1,5},{2,5},{3,5}are not in C(X).
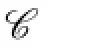
Claim 2{4,5}is not in C(Y),i.e.,{4,5}is not the color set of any vertex in Y.
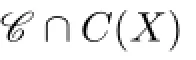
Claim 3One of the following 3 statements is valid:
(i){1,2,4},{1,2,5}/∈C(Y);
(ii){1,3,4},{1,3,5}/∈C(Y);
(iii){2,3,4},{2,3,5}/∈C(Y).
Otherwise,suppose that any one of the above 3 statements is not valid.One of{1,2,4},{1,2,5}is in C(Y),one of{1,3,4},{1,3,5}is in C(Y),one of{2,3,4},{2,3,5}is in C(Y).By Lemma 3.4,this implies that{1,2,3}⊆C(ui),i=1,2,...,7.So C(X)⊆{{1,2,3},{1,2,3,4},{1,2,3,5},[5]}.This is a contradiction.
Claim 4Suppose that{a,b,c}is a permutation of three colors 1,2 and 3.Then either{a,b,4},{a,b,5}/∈C(Y),or{a,c,4},{a,c,5}/∈C(Y).
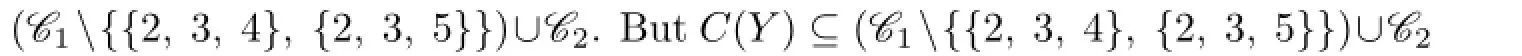
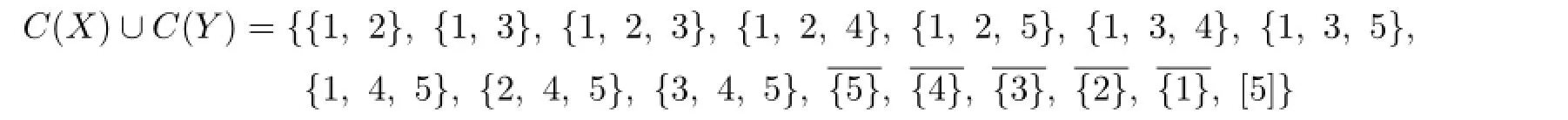
Therefore,{1,4,5},{2,4,5},{3,4,5}∈C(Y)and each C(ui)contains 4 or 5.This is a contradiction to{1,2},{1,3},{1,2,3}∈C(X).
From Claims 3 and 4,we deduce the following Claim 5.
Claim 5At least two of the following 3 statements are valid:
(i){1,2,4},{1,2,5}/∈C(Y);
(ii){1,3,4},{1,3,5}/∈C(Y);
(iii){2,3,4},{2,3,5}/∈C(Y).
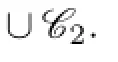
Claim 6{1,4},{2,4},{3,4},{1,5},{2,5},{3,5}/∈C(X).
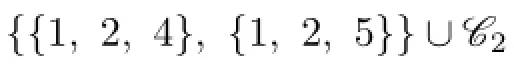
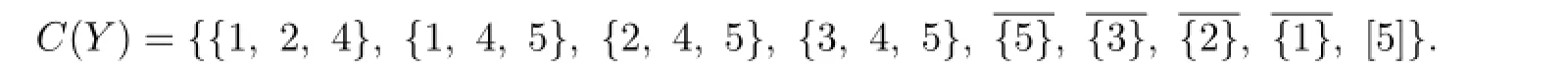
From{1,2,4}∈C(Y),we know that the color set of the color 1 or 2 vertex in X contains both 1 and 2.This is a contradiction to{1,4}∈C(X).
Claim 7At least one set among{1,4,5},{2,4,5},{3,4,5}does not belong to C(Y).
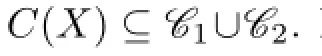
By Claim 7,we may assume that{3,4,5}/∈C(Y).Then
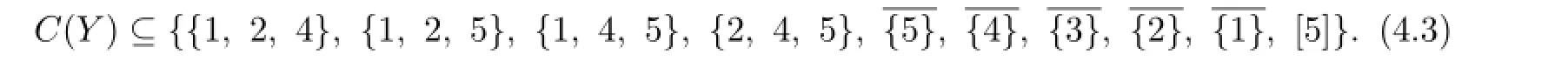
When n>1O a contradiction may appear.We suppose that n=9 or 1O in the following.
Claim 8At least one of two sets{1,4,5}and{2,4,5}is not in C(Y).
Otherwise{1,4,5},{2,4,5}∈C(Y)and the color sets of color 1 or 2 vertices in X contains 4 or 5.Since|C(Y)|=n≥9,one of two set{1,2,4},{1,2,5}belongs to C(Y),and the color set of color 1 vertex in X contains 2 and the color set of color 2 vertex in X contains 1.We may suppose g(ui)=i,i=1,2.Then
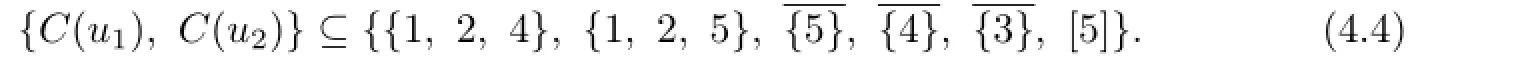
At least one set among the six subsets in the right side of(4.4),denoted by A,does not belongs to C(Y).From C(ui)/=C(vj),we know that C(u1)=A=C(u2),a contradiction.
By Claim 8,we may assume that{2,4,5}/∈C(Y).Thus n=9,and
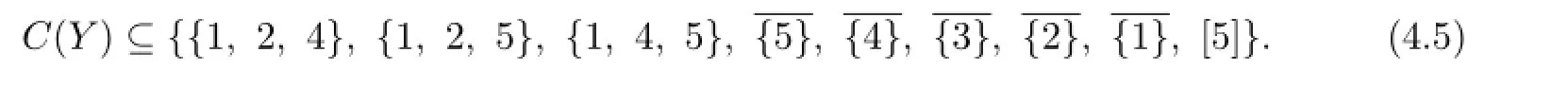
Claim 9{1,2},{1,3},{2,3}/∈C(X).
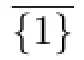
By Claim 9,we have
C(X)={{1,2,3},{1,3,4},{1,3,5},{2,3,4},{2,3,5},{2,4,5},{3,4,5}}. We may assume that C(u1)={2,4,5},C(v1)={1,2,4}.Then g(u1)=2,g(u1v1)=4 and g(v1)/∈{2,4},g(v1)=1.This is a contradiction.
Case 4 There are 4 different colors among g(u1),g(u2),...,g(u7).We may suppose that g(ui)∈{1,2,3,4},i=1,2,...,7.Then each 2-subset of{1,2,3,4,5}is not the color set of any vertex vjand each C(vj)is not{1,2,3},{1,2,4},{1,3,4},{2,3,4}or{1,2,3,4}.Let
Then We can obtain a contradiction if n≥12.So we suppose 9≤n≤11 in the following.
Claim 1Arbitrary 2-subset of{1,2,3,4}does not belongs to C(X).
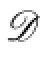
Claim 2{c,5}/∈C(X),c=1,2,3,4.
Otherwise,we may suppose that C(uio)={1,5}.Then g(uio)=1,g(uiovj)=5,and g(vj)/=5,j=1,2,...,n.But at least one of three sets{1,2,5},{1,3,5},{1,4,5}belongs to C(Y),say C(v1)={1,2,5}.Since g(uiov1)=5,g(v1)=1 or 2.This is a contradiction.
From Claims 1 and 2,we know that|C(ui)|≥3,i=1,2,...,7.Thus
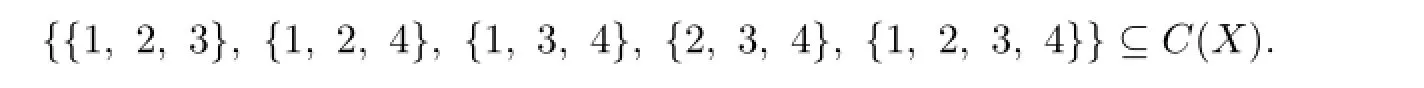
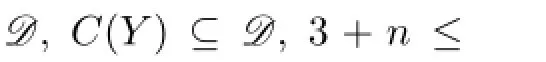
Claim 3{1,2,5},{1,3,5},{1,4,5},{2,3,5},{2,4,5},{3,4,5}/∈C(X). Otherwise,we may assume that C(u6)={1,2,5}.
When g(u6)=1,then g(u6vj)=2 or 5.But one of two sets{1,3,5},{1,4,5}belongs to C(Y),say C(v1)={1,4,5}.Then g(u6v1)=5 and g(v1)∈{1,4}.This is a contradiction.
When g(u6)=2,then g(u6vj)=1 or 5.But one of two sets{2,3,5},{2,4,5}belongs to C(Y),say C(v2)={2,4,5}.Then g(u6v2)=5 and g(v2)∈{2,4}.This is a contradiction.
From Claim 3 and Lemma 3.5,we know that{1,2,3,4}⊆C(ui),i=1,2,...,7.Then C(X)⊆{{1,2,3,4},{1,2,3,4,5}}.This is a contradiction.
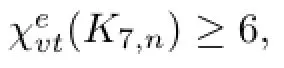
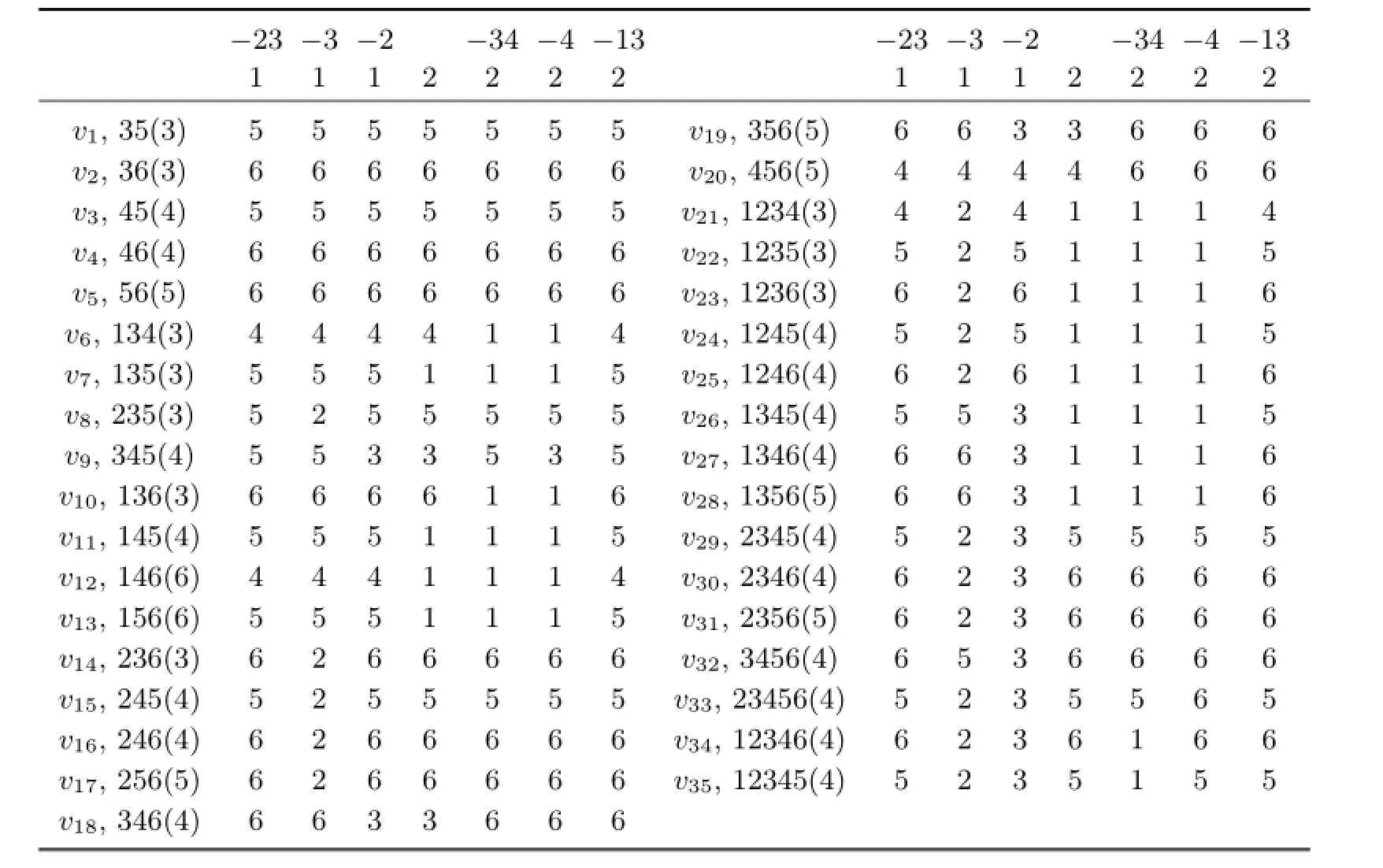
Table 4.1A 6-VDET coloring f35of K7,35
The proof of Theorem 4.1 is completed.
Proof.Assume that K7,nhas a 6-VDET coloring g.There are five cases to consider.
Case 1 u1,u2,...,u7receive the same color under g.
Case 2 u1,u2,...,u7receive two different colors under g.
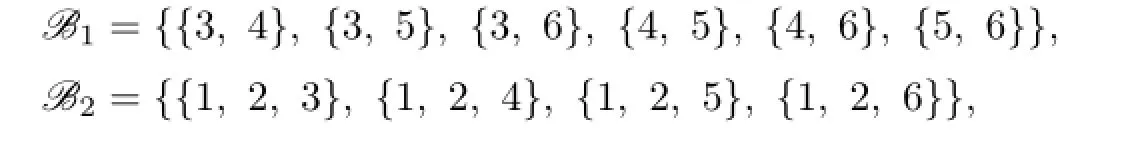
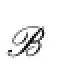
In this time,by Lemma 3.1,we have that 1,2∈C(ui),i=1,2,...,7.If C(u1)∩C(u2)∩...∩C(u7)∩{3,4,5,6}has at least two colors,say it contains 3 and 4,then C(X)⊆{{1,2,3,4},{1,2,3,4,5},{1,2,3,4,6},[6]}.This is a contradiction.If C(u1)∩C(u2)∩...∩C(u7)∩{3,4,5,6}has just one color,say 3,then{4,5},{4,6},{5,6},{5,6,7}/∈C(Y).When{1,4,5},{2,4,5}∈C(Y),by Lemma 3.3,each C(ui)contains 4 or 5,then
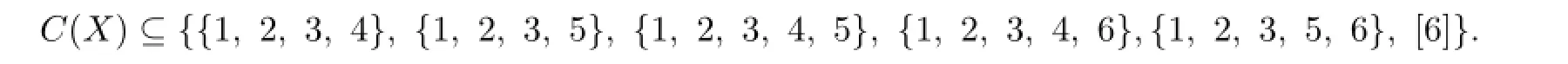
This is a contradiction.Similarly,when{1,4,6},{2,4,6}∈C(Y),or{1,5,6},{2,5,6}∈C(Y),we can obtain a contradiction.
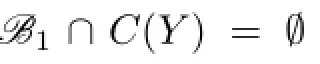
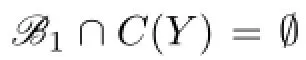
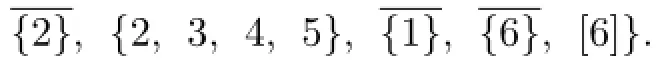
Case 3 u1,u2,u3and u4receive three different colors under g.
We may suppose that g(ui)∈{1,2,3}.Then the color set C(vj)does not include color i when|C(vj)|=2,i=1,2,3,and each C(vj)is not{1,2,3}.
Claim 1Each C(ui)contains at least three colors.
Claim 2{1,2,3}/∈C(X).
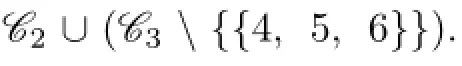
By Claim 2,we have C(X)∪C(Y)⊆C and 7+n≤44,n≤37,n=36,37.
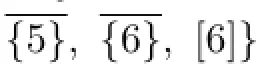
Case 4 There are 4 different colors among g(u1),g(u2),...,g(u7).
Claim 1Arbitrary 2-subset of{1,2,3,4,5,6}does not belongs to C(X).
By Claim 1,we have
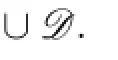
Claim 2At least one of the following 6 statements are valid:
(i){1,2,5},{1,2,6}/∈C(Y);
(ii){1,3,5},{1,3,6}/∈C(Y);
(iii){1,4,5},{1,4,6}/∈C(Y);
(iv){2,3,5},{2,3,6}/∈C(Y);
(v){2,4,5},{2,4,6}/∈C(Y);
(vi){3,4,5},{3,4,6}/∈C(Y).
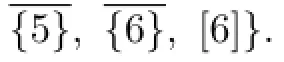
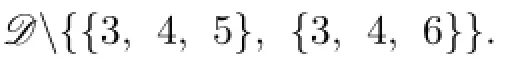
Case 5 There are 5 different colors among g(u1),g(u2),...,g(u7).
We may suppose that g(ui)∈{1,2,3,4,5},i=1,2,...,7.Let E denote the set composed by the 6-subsets of[6],5-subsets of[6]which contain 6,4-subsets of[6]which contain 6,3-subsets of[6]which contain 6.Then E contains 26 members.But C(Y)⊆D. This is a contradiction.
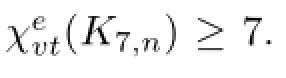
We determine f95firstly.Let the subgraph of K7,95induced by X∪{v1,v2,...,v35}be colored using the 6-VDET coloring f35given in Table 4.1.And then color other vertices and incident edges.Let v36,v37,...,v46be corresponded to{3,7},{1,4,5,6},{1,2,4,5,6},{1,3,4,5,6},{1,2,3,4,5,6},{1,2,5,6},{1,2,3,5,6},{2,4,5,6},{4,7},{5,7},{6,7}.
Let v47,v48,...,v60be corresponded to the 3-subsets of[7]which contain 7 and are not{1,2,3}.Let v61,v62,...,v80be corresponded to the 4-subsets of[7]which contain 7.Let v81,v82,...,v92be corresponded to the 5-subsets of[7]which contain 7 and are not{1,4,5,6,7},{2,4,5,6,7},{1,2,5,6,7}.Let v93,v94,v95be corresponded to the 5-subsets of[7]which contain 7 and are not{2,3,4,5,6,7},{1,2,3,4,6,7},{1,2,3,4,5,7}.
Suppose that D(vj)is the set corresponding to vertex vj(36≤j≤95).Since u5vjmay receive color 1,u2vjmay receive color 2,u6vjmay receive color 3,u3vjmay receive color 4,every edge may receive colors 5,6,7,we can assign appropriate colors in D(vj)to vjand its incident edges such that C(vj)=D(vj)and the resulting coloring is VDET coloring.For detail of this coloring we can see Table 4.2.
The restriction of 7-VDET coloring f95of K7,95on its subgraph induced by{u1,u2,...,u7,v1,v2,...,vi}is obviously a 7-VDET coloring fi,where 36≤i≤95.The proof of Theorem 4.2 is completed.
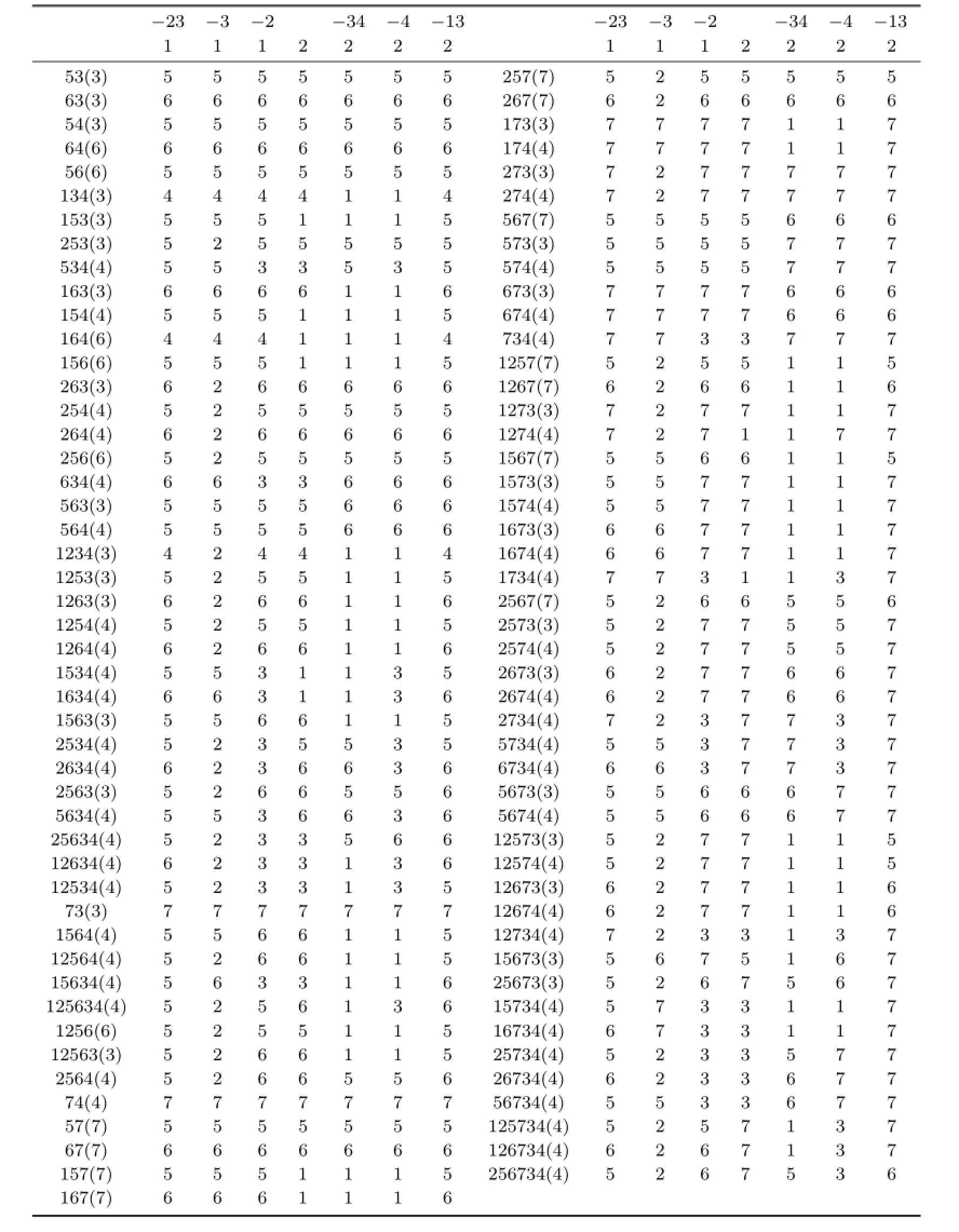
Table 4.2A 7-VDET coloring of K7,95
5 Conclusion
By simple computation,we have
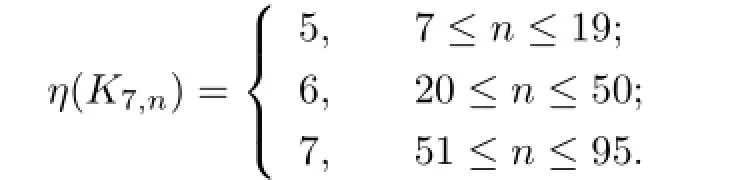
From Proposition 2.1 and Theorems 4.1 and 4.2,we know that
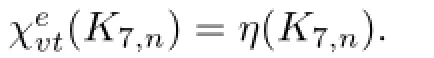
Thus Conjecture 1.1 is right for K7,n(7≤n≤95).
References
[1]ˇCern´y J,Horˇn´ak M,Sot´ak R.Observability of a graphs.Math.Slovaca,1996,46:21-31.
[2]Burris A C,Schelp R H.Vertex-distinguish proper edge-colorings.J Graph Theory,1997,26:73-82.
[3]Balister P N,Kostochka A,Li H,Schelp R H.Balanced edge colorings.J.Comb.Theory,Series B,2OO4,90:3-2O.
[4]Balister P N,Riordan O M,Schelp R H.Vertex-distinguishing edge colorings of graphs.J. Graph Theory,2OO3,42:95-1O9.
[5]Liu B,Liu G Z.Vertex-distinguishing edge colorings of graphs with degree sum conditions. Graphs Combin.,2O1O,26(6):781-791.
[6]Ruda˘sov´a J,Sot´ak R.Vertex-distinguishing proper edge colorings of some regular graphs. Discrete Math.,2OO8,308:795-8O2.
[7]Taczuk K,Wo´zniak M.A note on the vertex-distinguishing index for some cubic graphs. Opuscula Math.,2OO4,24(2):223-229.
[8]Harary F,Plantholt M.The point-distinguishing chromatic index.in:Harary F,Maybee J S. Graphs and Application.New York:Wiley Interscience,1985:147-162.
[9]Chen X E.Point-distinguishing chromatic index of the union of paths.Czechoslovak Math.J.,2O14,64(3):629-64O.
[1O]Horˇn´ak M,Sot´ak R.The fifth jump of the point-distinguishing chromatic index of Kn,n.Ars Combin.,1996,42:233-242.
[11]Horˇn´ak M,Sot´ak R.Localization jumps of the point-distinguishing chromatic index of Kn,n. Discuss.Math.Graph Theory,1997,17:243-251.
[12]Horˇn´ak M,Zagaglia Salvi N.On the point-distinguishing chromatic index of complete bipartite graphs.Ars Combin.,2OO6,80:75-85.
[13]Zagaglia Salvi N.On the point-distinguishing chromatic index of Kn,n.Ars Combin.,1988,25B:93-1O4.
[14]Zagaglia Salvi N.On the value of the point-distinguishing chromatic index of Kn,n.Ars Combin.,199O,29B:235-244.
[15]Zhang Z F,Yao B,Li J W,Liu L Z,Wang J F,Xu B G.Vertex-distinguishing total colorings of graphs.Ars Combin.,2OO8,87:33-45.
[16]Chen X E.Asymptotic behaviour of the vertex-distinguishing totsl chromatic numbers of ncubes(in Chinese).J.Northwest Norm.Univ.Nat.Sci.Ed.,2OO5,41(5):1-3.
[17]Chen X E,Gao Y P,Yao B.Relations of vertex-distinguishing total chromatic numbers between a subgraph and its supergraph.Inform.Sci.,2O14,288:246-253.
[18]Chen X E,Zu Y,Xu J,Wang Z W,Yao B.Vertex-distinguishing E-total colorings of graphs. Arab.J.Sci.Eng.,2O11,36:1485-15OO.
[19]Chen X E,Zu Y.Vertex-distinguishing E-total coloring of the graphs mC3and mC4.J.Math. Res.Exposition,2O11,31:45-58.
[2O]Bondy J A,Murty U S R.Graph Theory.London:Springer,2OO8.
1O.13447/j.1674-5647.2O16.O4.O8
date:Sept.22,2015.
The NSF(61163037)of China.
E-mail address:chenxe@nwnu.edu.cn(Chen X E).
Communicated by Du Xian-kun
杂志排行
Communications in Mathematical Research的其它文章
- On Reducibility of Beam Equation with Quasi-periodic Forcing Potential
- Fock-Sobolev Spaces and Weighted Composition Operators among Them
- A Remark on Adaptive Decomposition for Nonlinear Time-frequency Analysis
- Bayesian Estimation for the Order of INAR(q)Model
- The Twin Domination Number of Strong Product of Digraphs
- A Generalization of Gorenstein Injective and Flat Modules
