On Reducibility of Beam Equation with Quasi-periodic Forcing Potential
2016-11-19CHANGJING
CHANG JING
(1.College of Information Technology,Jilin Agricultural University,Changchun,130118)
(2.School of Mathematics,Jilin University,Changchun,130012)
On Reducibility of Beam Equation with Quasi-periodic Forcing Potential
CHANG JING1,2
(1.College of Information Technology,Jilin Agricultural University,Changchun,130118)
(2.School of Mathematics,Jilin University,Changchun,130012)
In this paper,the Dirichlet boundary value problems of the nonlinear beam equation utt+∆2u+αu+ϵϕ(t)(u+u3)=O,α>O in the dimension one is considered,where u(t,x)and ϕ(t)are analytic quasi-periodic functions in t,and ϵ is a small positive real-number parameter.It is proved that the above equation admits a small-amplitude quasi-periodic solution.The proof is based on an infinite dimensional KAM iteration procedure.
beam equation,infinite dimension,Hamiltonian system,KAM theory,reducibility
2010 MR subject classification:37K55,35B15
Document code:A
Article ID:1674-5647(2O16)O4-O289-14
1 Introduction and Main Result
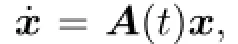
Bogolyubov[3]proved reducibility of non autonomous finite-dimensional linear systems to constant coefficient equations by KAM's method.Since then,the reducibility of finitedimensional system can be dealt by means of the KAM tools.Then,for infinite dimensional system in[4],Dinaburg and Sinai proved that the linear Schr¨odinger equation
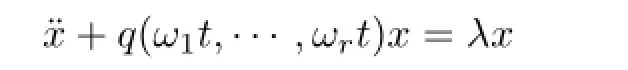
is reducible for“most”large enough λ,when ω is fixed and satisfies the Diophantine conditions
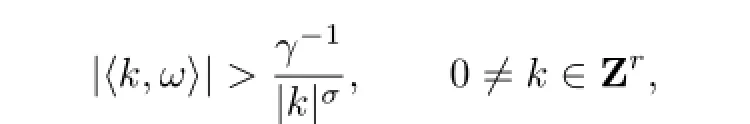
where γ>1,σ>r-1 are fixed positive constants.The latest result is in[5],Eliasson and Kuksin proved that the linear d-dimensional Schr¨odinger equation
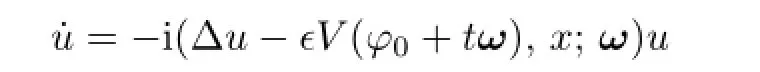
about x-periodic and t-quasi-periodic,which can be reduced to an autonomous equation for most values of the frequency vector ω by KAM theory.
In this paper,we prove that the non-autonomous nonlinear beam equation admits smallamplitude quasi-periodic solution.The important point is to reduce the beam equation to the system which can be used by KAM theory.
Consider the following nonlinear beam equation with Dirichlet boundary conditions:
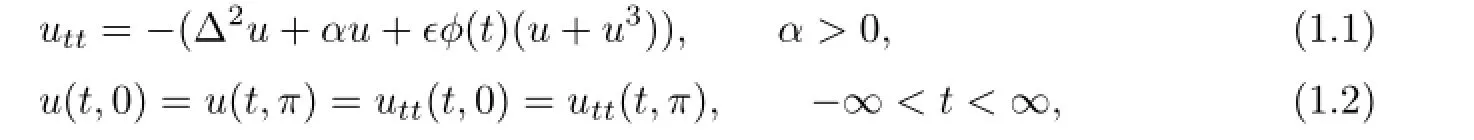
where ϵ is a small positive parameter,ϕ(t)is a real analytic quasi-periodic function in t with frequency vector ω=(ω1,ω2,...,ωd)⊂Rd.Considering the non-autonomous equation(1.1)in the complex Hilbert space ℓa,ρ,first,we choose any fixed lattice points
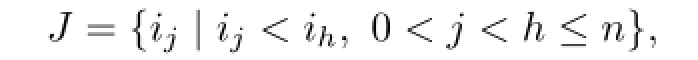
without loss of generality,we suppose J={1,2,...,n}.
Let A=-∆2+α.The eigenvalues and eigenfunctions of the operator A with Dirichlet boundary conditions are as follows
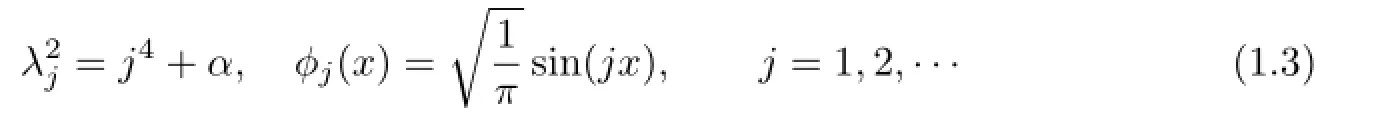
When ϵ=O in(1.1),the solution of the linear equation
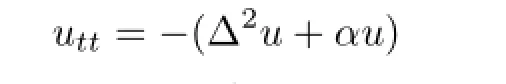
with Dirichlet boundary conditions are given by
Let us state our main result as follows.
Theorem 1.1Consider the 1D nonlinear beam equation(1.1)with Dirichlet boundary condition(1.2),where ϕ(t)is quasi-period function with t.For each index J={j1<j2<...<jn}and all α>O,there exists a Cantor set O*⊂O such that ξ∈O*.Then the boundary value problem(1.1)-(1.2)has a linearly stable quasi-period solution.
2 The Hamiltonian for 1D Beam Equations
Let v=utand A=-(∆2+α),x,t∈R.Then(1.1)can be read as
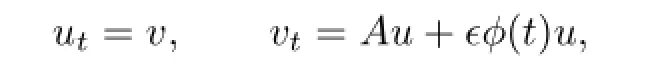
which may be viewed as the(infinite-dimensional)Hamiltonian equations
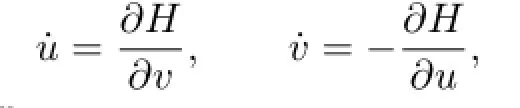
associated with the Hamiltonian
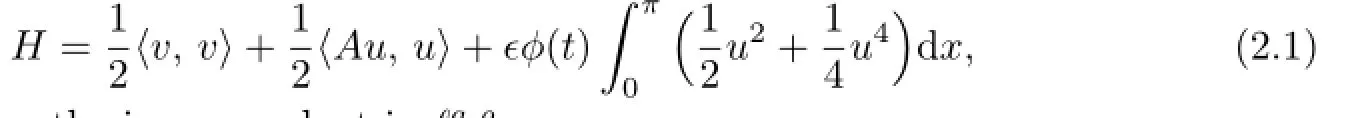
where〈.,.〉denotes the inner product in ℓa,ρ.
We introduce coordinates q=(q1,q2,...),p=(p1,p2,...)with finite norm
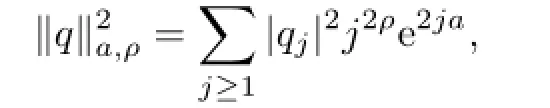
where a≥O and ρ>O,which satisfies the following relationship
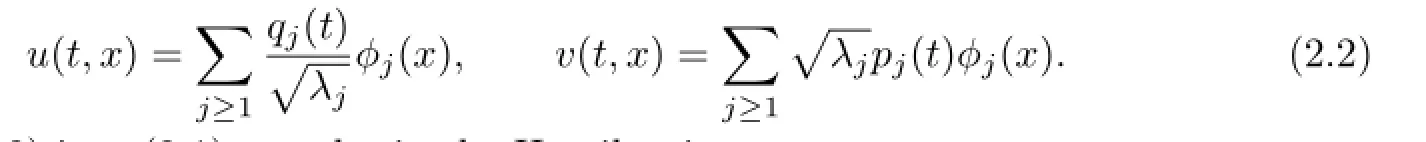
Substituting(2.2)into(2.1),we obtain the Hamiltonian
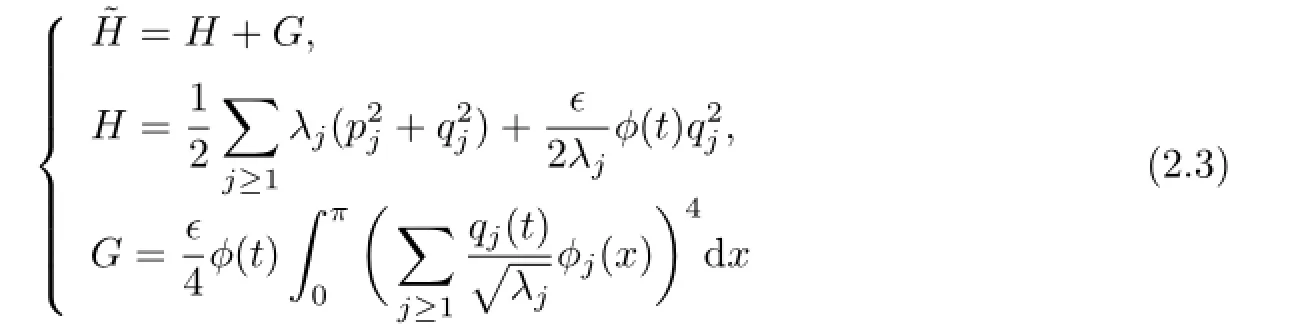
with respect to the symplectic structuredqj∧dpjon ℓa,ρ×ℓa,ρ.
Lemma 2.1Let a≥O and ρ>O,I be an interval,and I∋t-→(q(t),p(t))be a real analytic solution of(2.3).Then
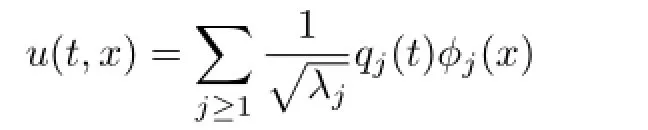
is a real analytic solution of(2.1)on I×[O,π].
Let φ(θ)=φ(θ1,...,θd)=φ(w1t,...,wdt)=ϕ(t).Then(2.2)can be changed into
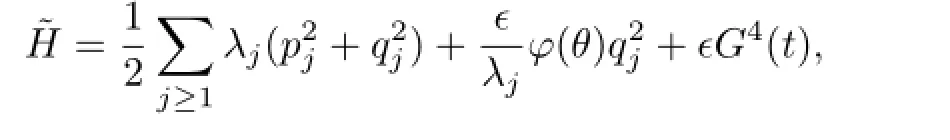
where
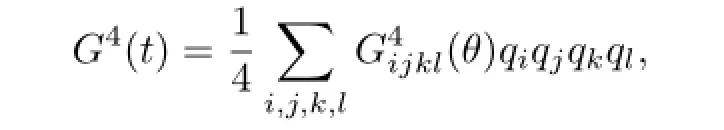
and the coefficients
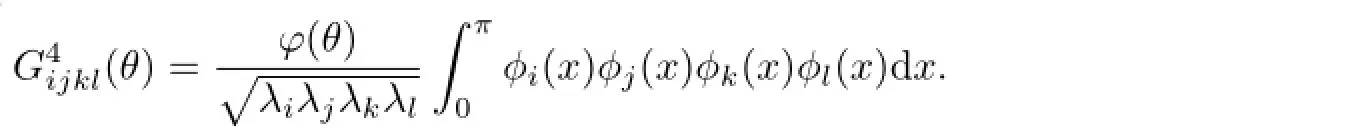
An easy computation show that Gijkl=O unless if i±j±k±l/=O.In particular,we have

Before proving Theorem 1.1,we first switch to complex variables
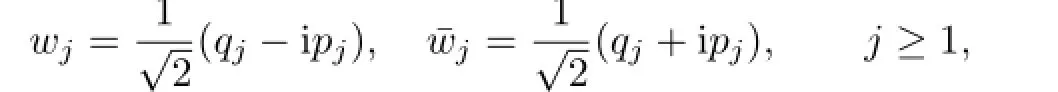
and introduce standard action-angle variables
Then we have the Hamilton system
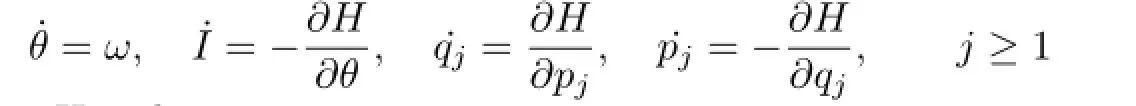
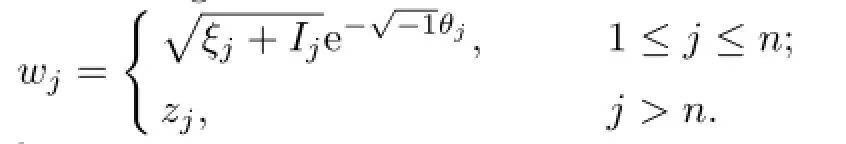
with the following Hamiltonian
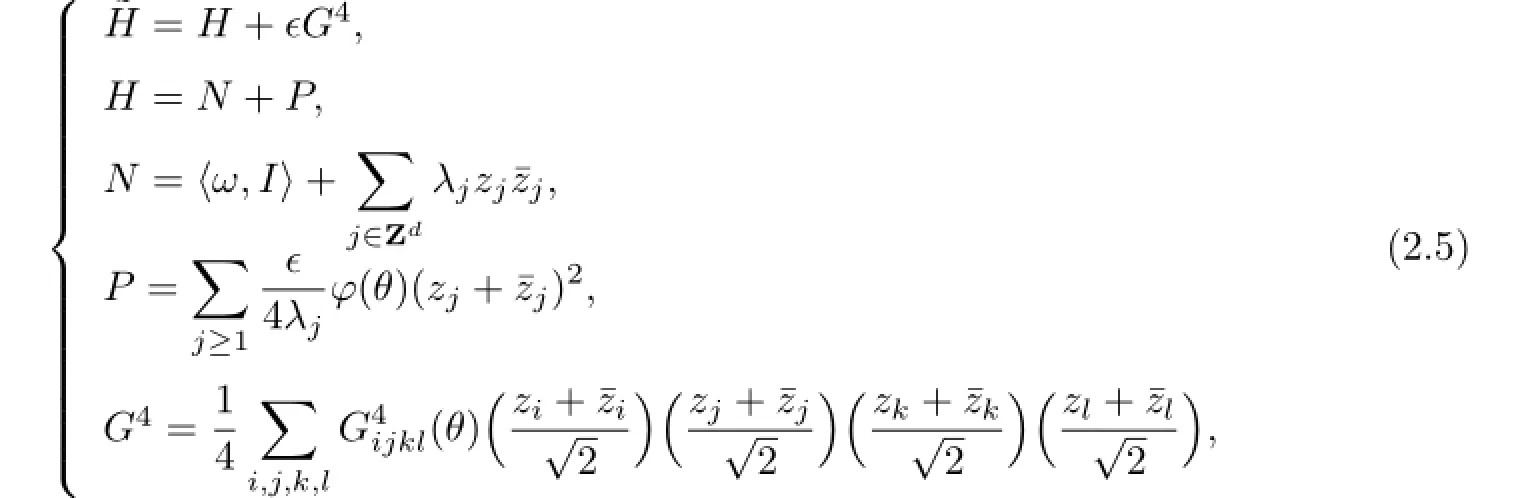
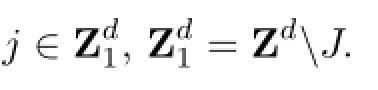
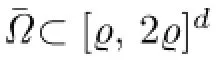
(i)There is a constant with
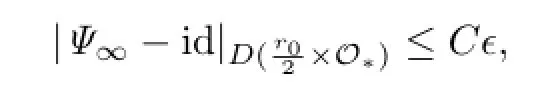
where id is identify map.
(ii)Ψ∞can transformed(2.5)into

In the following,our goal is to investigate the reducibility of Hamiltonian(2.5)by KAM iteration.
At the same time,we expand P into the Fourier-Taylor series
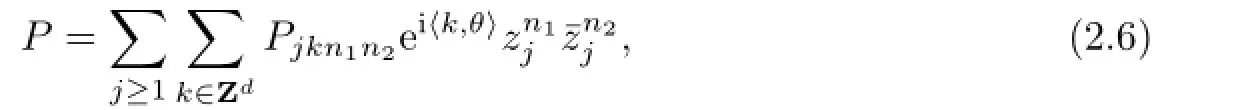
and let R be the truncation of P given by
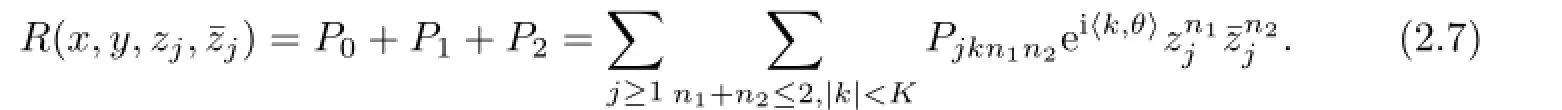
Next,we prove Theorem 3.1 by a KAM iteration,which involves an infinite sequence of change of variables.At each step of KAM iteration,we reduce angle variable θ and make the perturbation smaller than that in the previous step.In the last,we prove the convergence of the iteration and estimate the measure of the excluded set after infinite KAM step.
2.1KAM Step
First,we show detailed KAM iteration.Initially,we set the initial values ϵ=ϵ0,λj,0=λj,
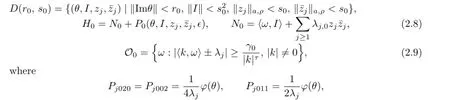
furthermore,‖XPo‖D(ro,so),Oo≤ϵ0.Suppose that after vth KAM step,we arrive at
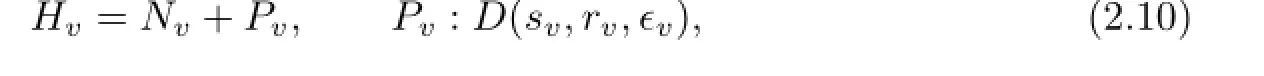
where
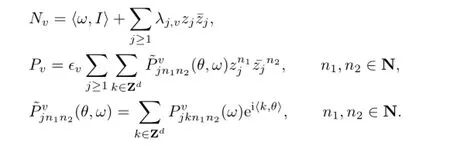
Furthermore,
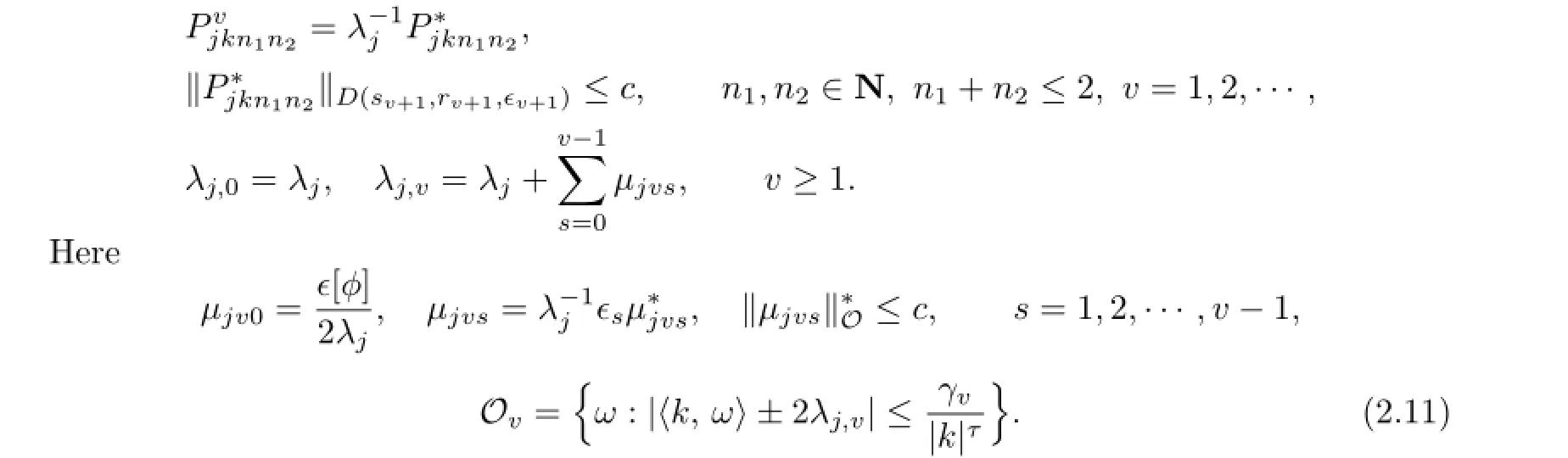
To simplify notations,the quantities without subscripts refer to quantities at the vth step,while the(v+1)th step which will be subscripted by+.We wish to find a special function F=Fv=ϵvF defined on a smaller domain D+=D(r+,s+),such that a symplectic transformation Φ+which is in smaller frequency and phase domains.Then transformation Φ+carries the above Hamiltonian into the next KAM cycle.The transformed Hamiltonian should be of a form similar to(2.1O)with a smaller perturbation term.
Then we construct a map
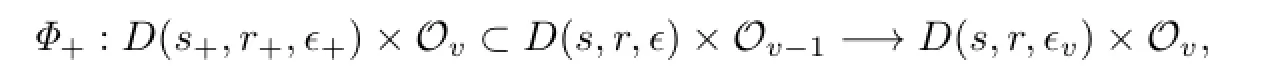
such that the vector field XH◦Φdefined on D(r+,s+,ϵ+)satisfies
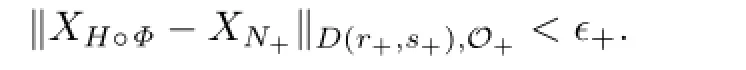
Now,we consider the Hamiltonian H=N+P defined in D(r,s)×O.And we suppose that ξ∈O satisfies the following

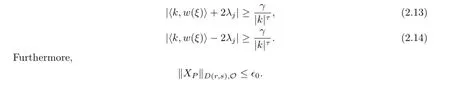
2.2The Homological Equation
Let
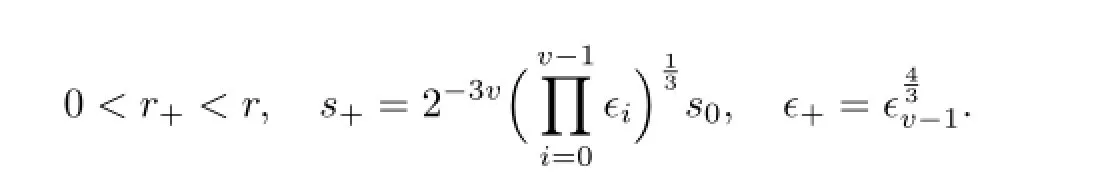

By the second order Taylor formula,we have
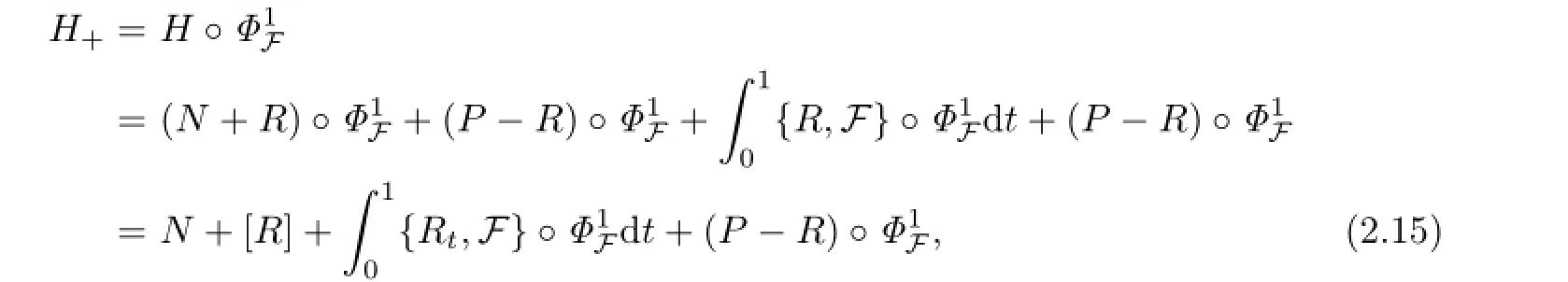
where
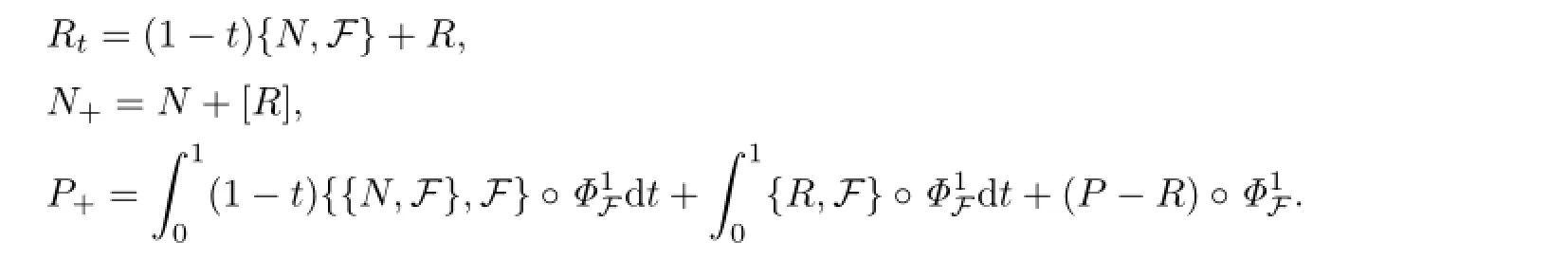
Thus
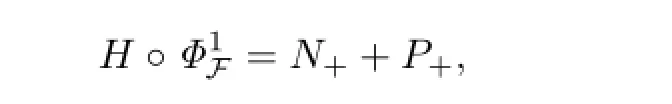
where the function F is determined by the homological equation as follows:
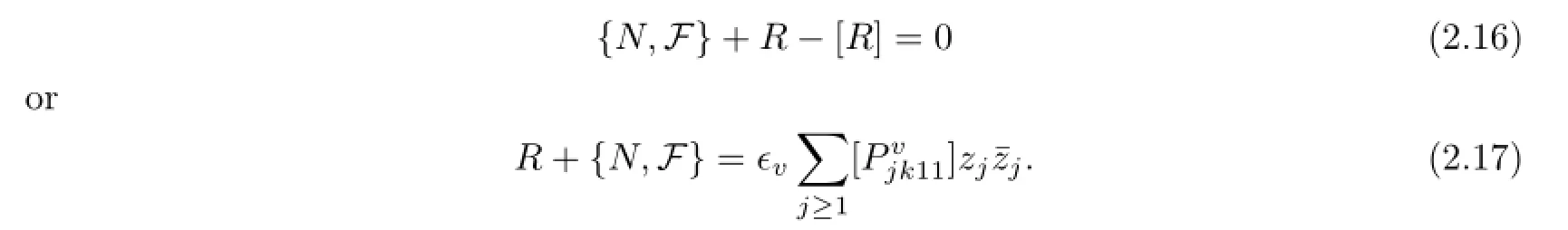
Then(2.15),(2.16)and(2.17)are equivalent to the following equations:
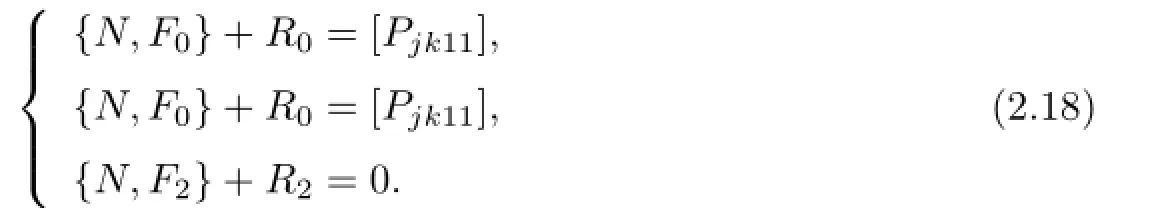
By Cauchy estimate,we have
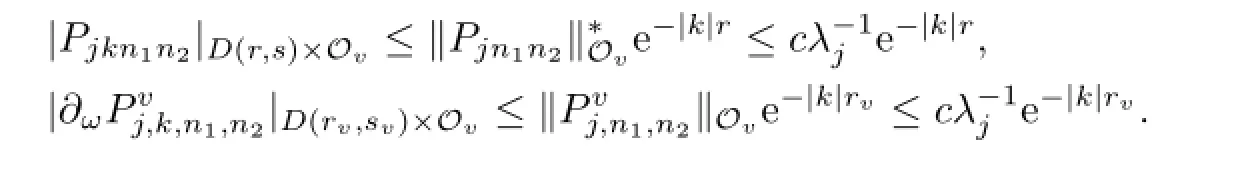
So
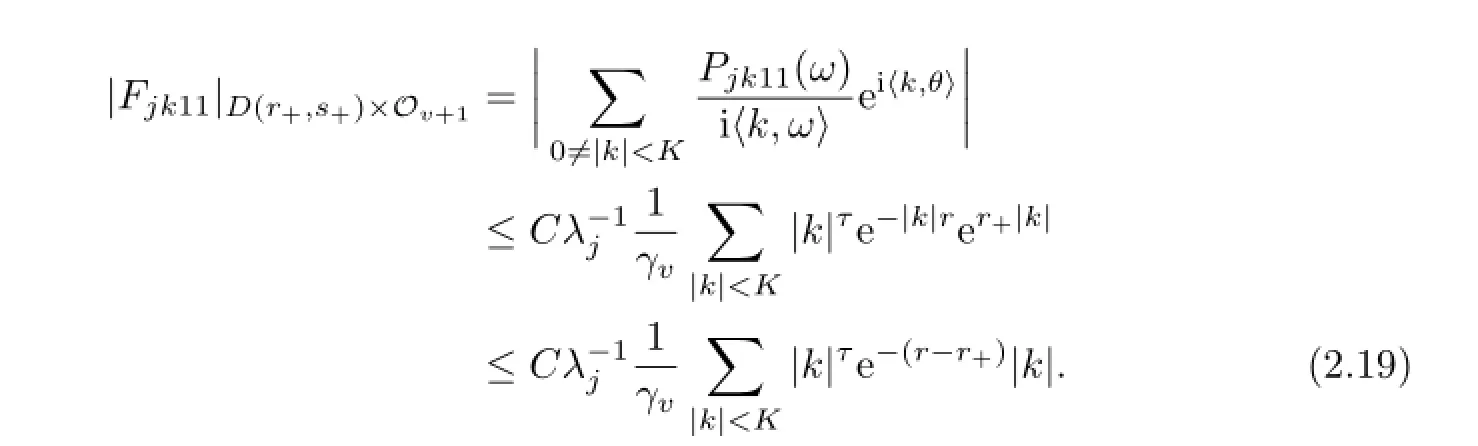
At the same idea,the following inequality can be arrived
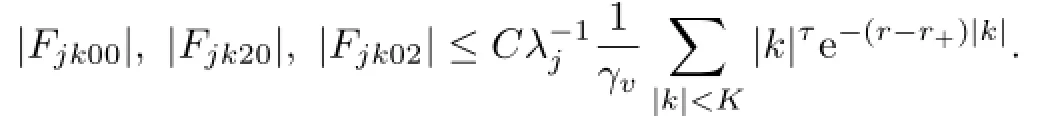
Next,we proceed to estimate XF.Similar to the above discussion,we get the following estimates:
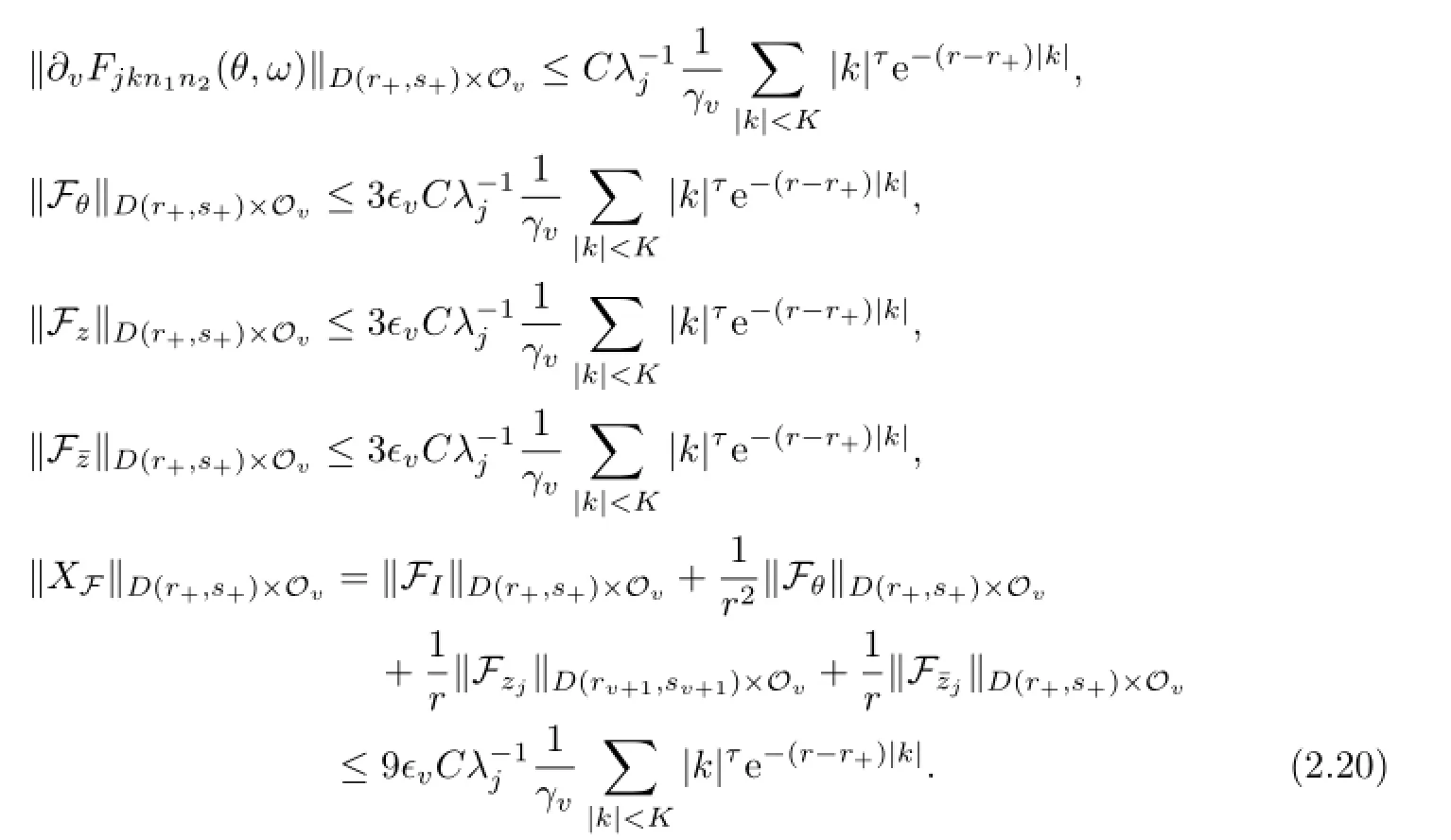
Lemma 2.2For δ>O and ν>O,the following inequality holds true:
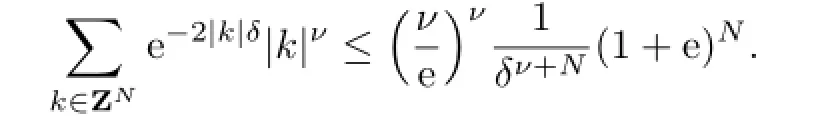
The proof can be found in[3].By Lemma 2.2 and(2.2O),we can get
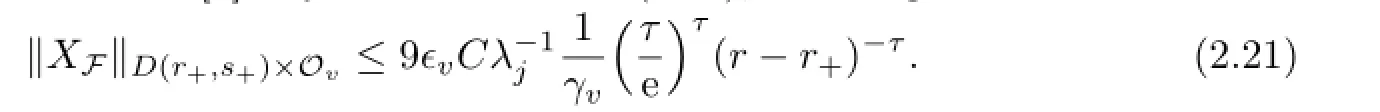
This can be shown in the following lemma.
Lemma 2.3Define
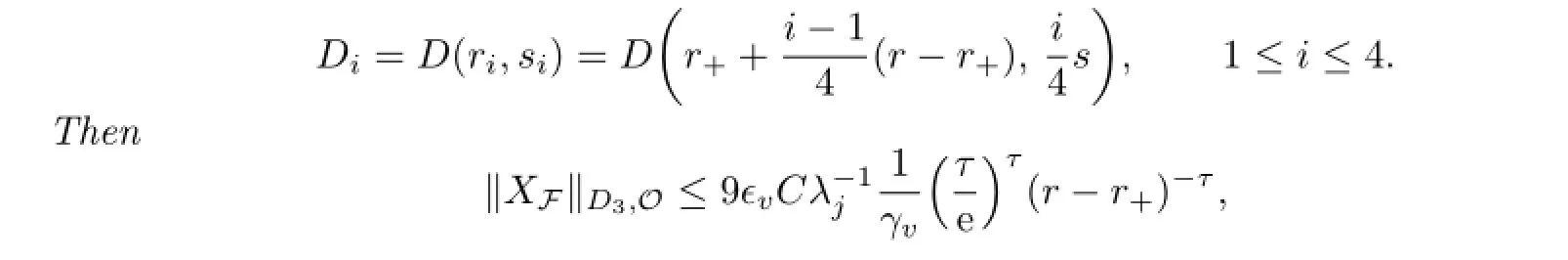
where C is a constant.
2.3Estimation for the New Perturbation
In order to the KAM step continue,we have to estimate the new perturbation term. Lemma 2.4If‖XF‖D(r,s)<ϵ′and‖XG‖D(r,s)<ϵ′′,then
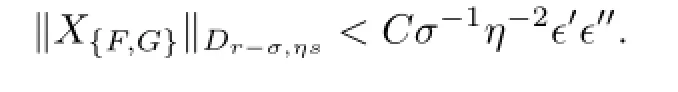
Proof.See[6].
By the paper[7],we have the following result
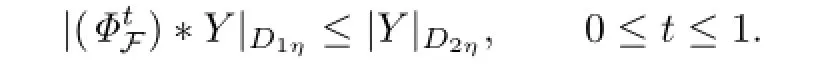
By Lemma 2.4,we get

and
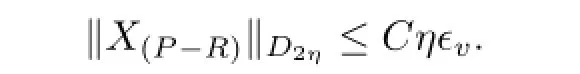
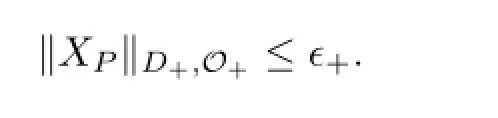
3 Iteration Lemma and Convergence
We define s,r,γ,ϵ as following sequences
We assume that ω satisfies the following relations:
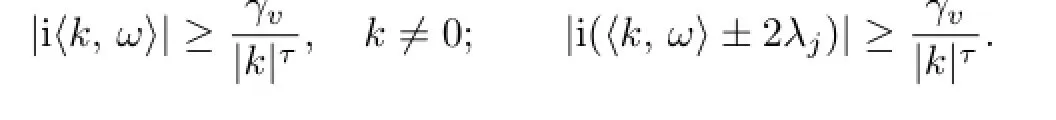
3.1Estimate on the Transformation Φ

then we have that
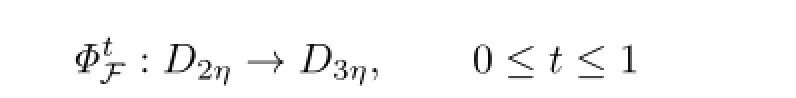
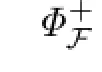
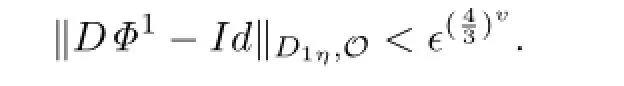
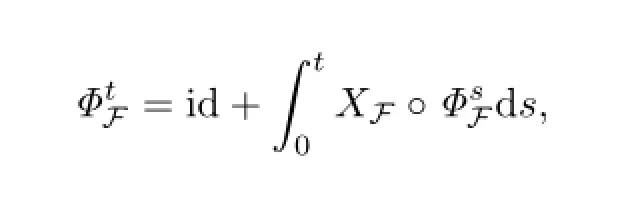
thus from(2.2O),if
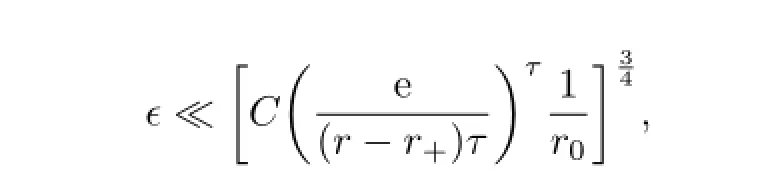
then we get
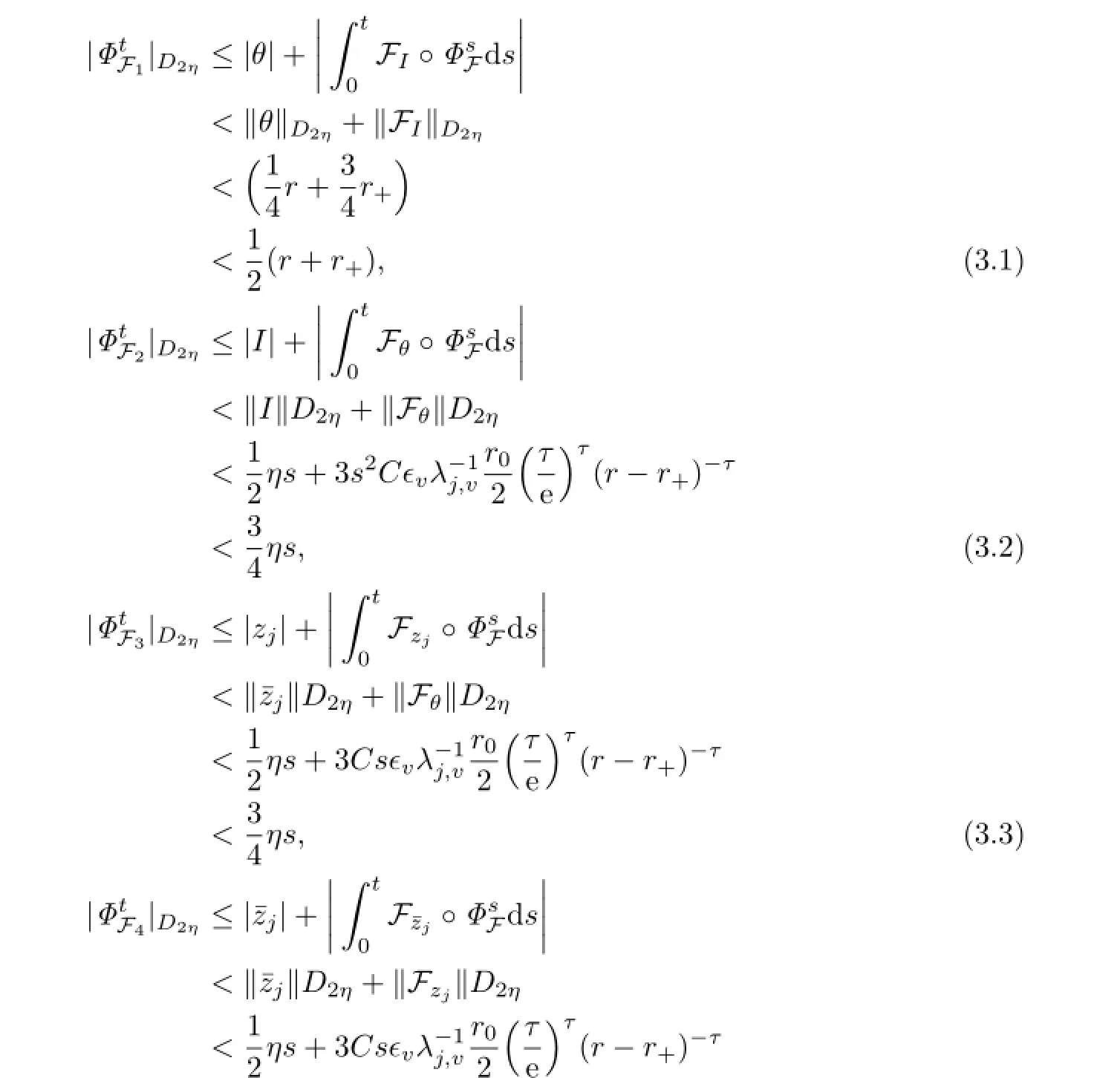
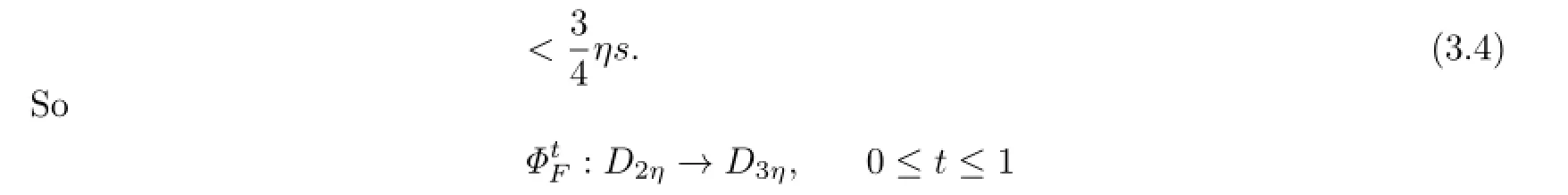
is well defined.Let
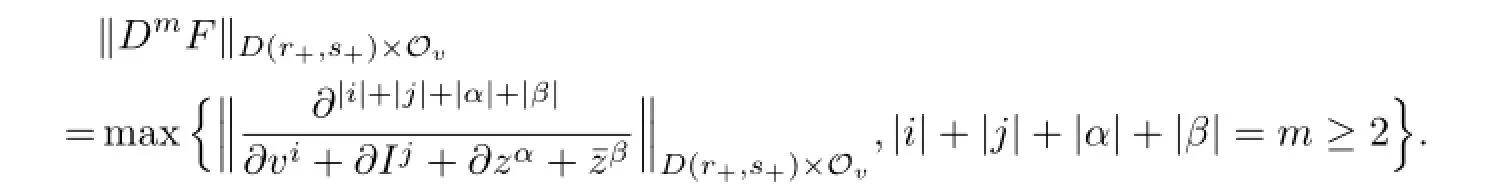
By Cauchy inequality,it follows that
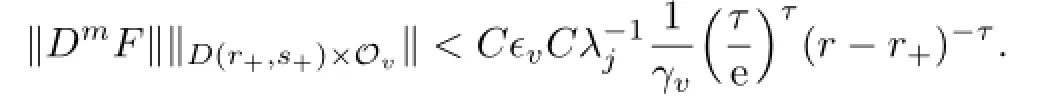

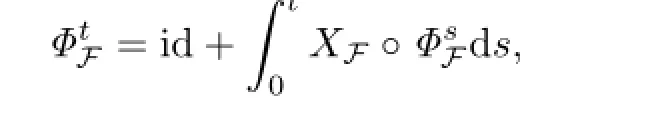
and
where
We get

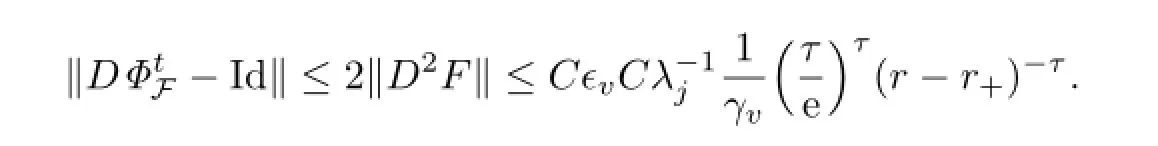
3.2Convergence
In this subsection,the iteration procedure is proved to be convergent.Let
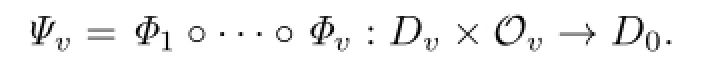
Noting that
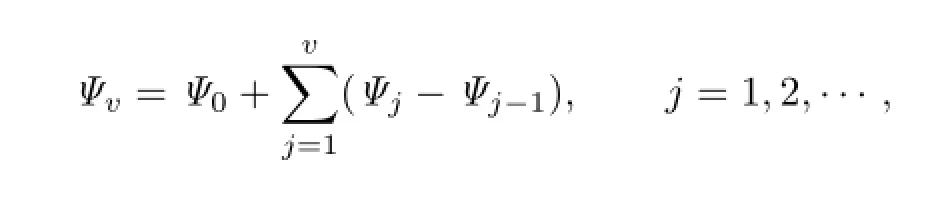
we have
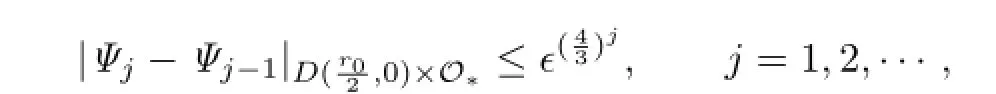
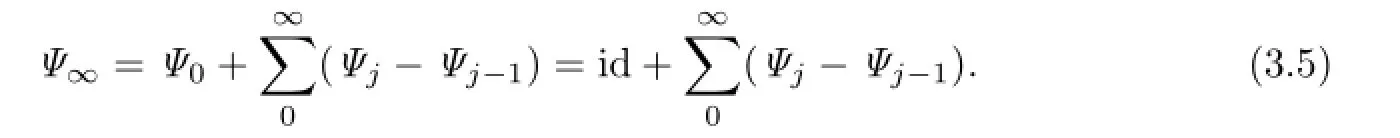


4 Measure Estimates
We throw away the following resonant set.Let
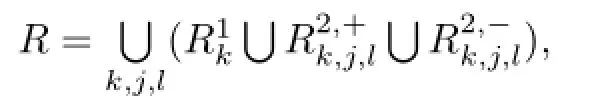
where
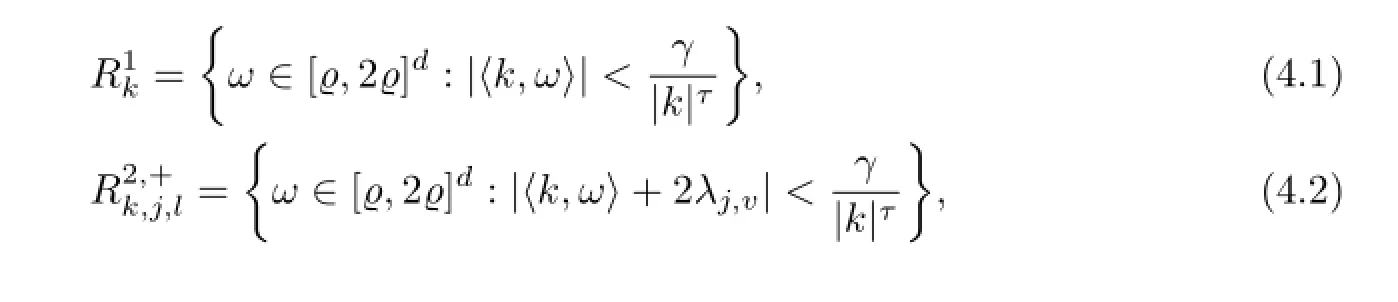
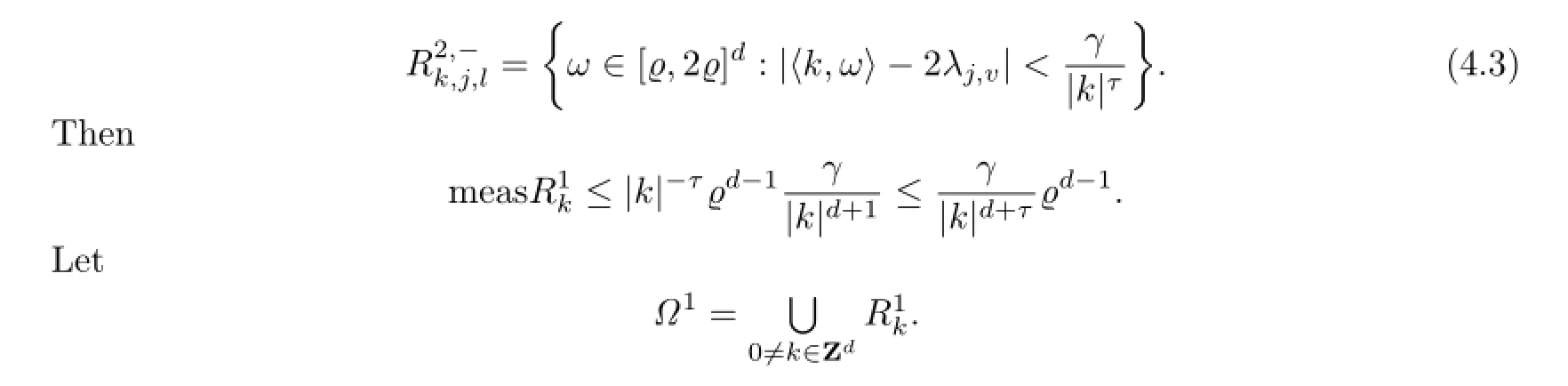
Then we can get
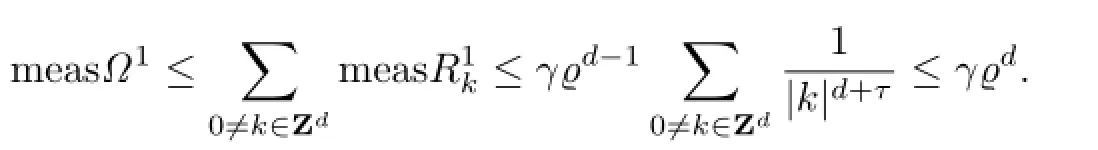
For fixed O<γ<1,we have
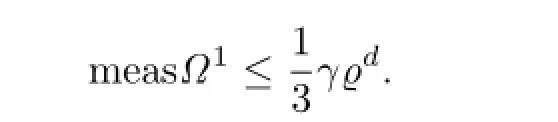
Let Ω00=[ϱ,2ϱ]Ω1.Then
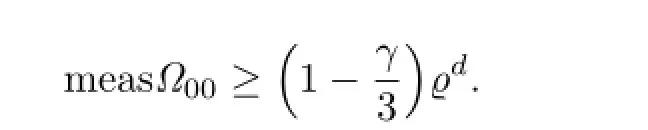
If we let
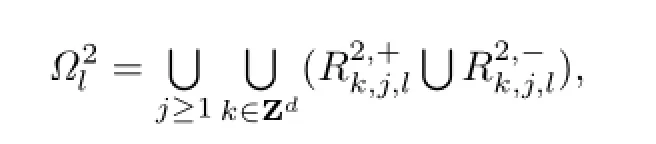
in the same idea,we have

Let
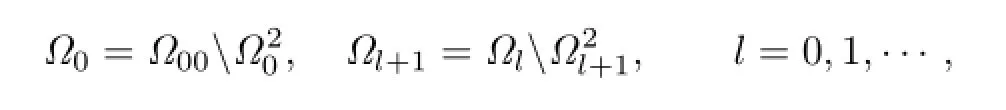
and
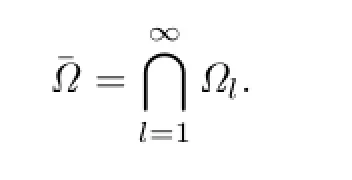
In the following,we prove the existence of quasi-period solutions by using KAM theory.

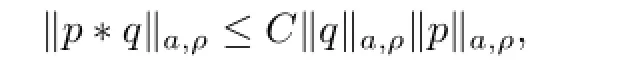
where the constant C depends only on ρ.
By using the above lemma,we can prove the following lemma.
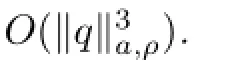
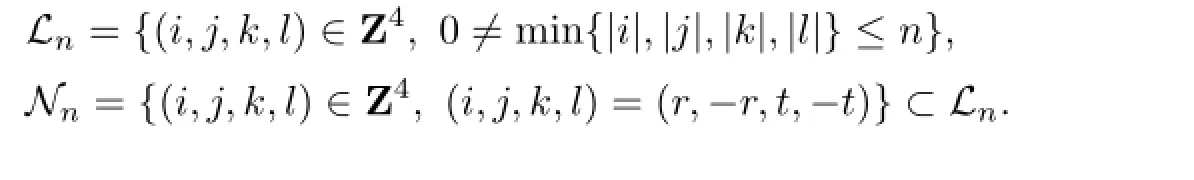

If i,j,k,l are non-zero integers such that i±j±k±l=O,but(i,j,k,l)/=(r,-r,t,-t),then for ϱ>O,O<γ<1,and parameter ω∈¯Ω,
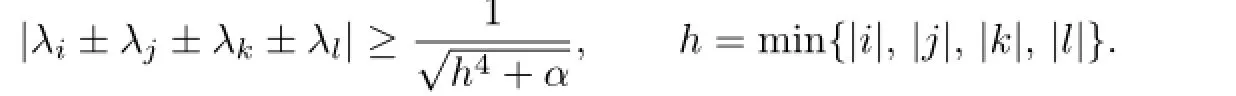
Proof.See[8].
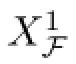
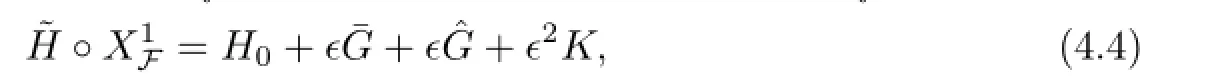
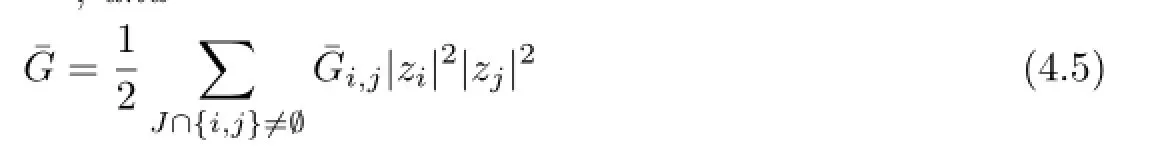
with uniquely determined coefficients
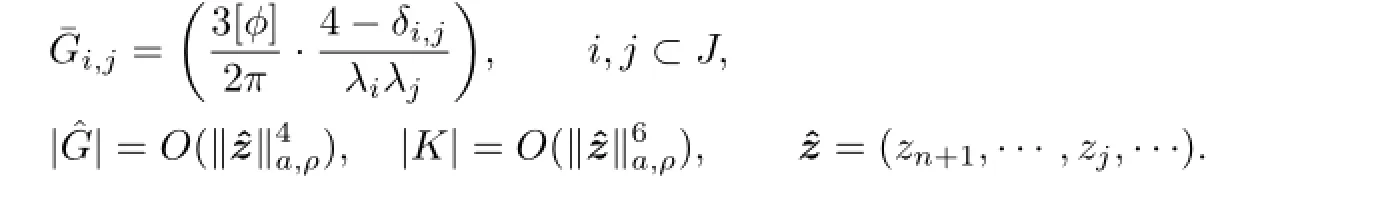

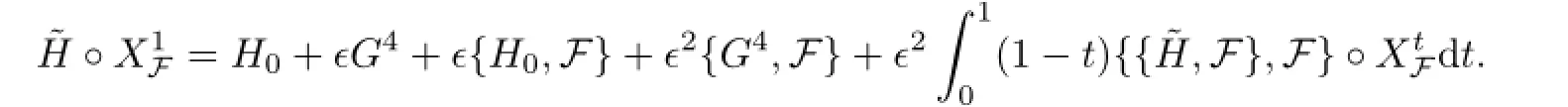
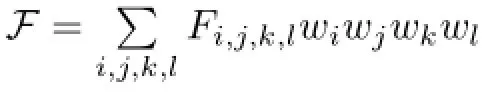
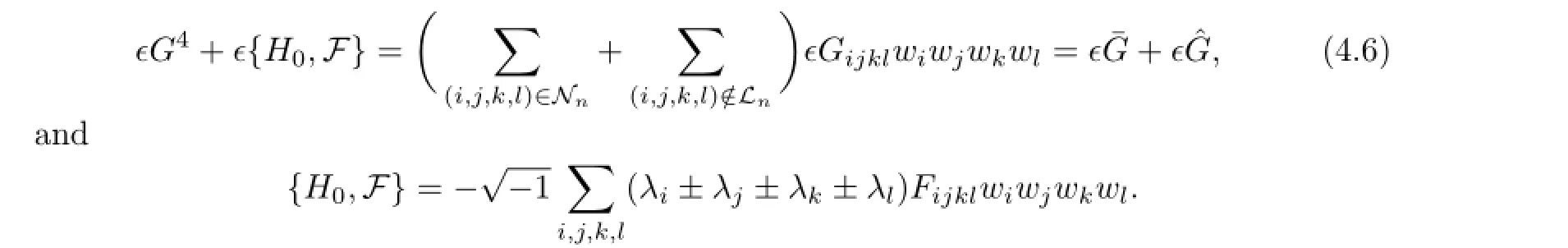
By Lemma 4.1,we have
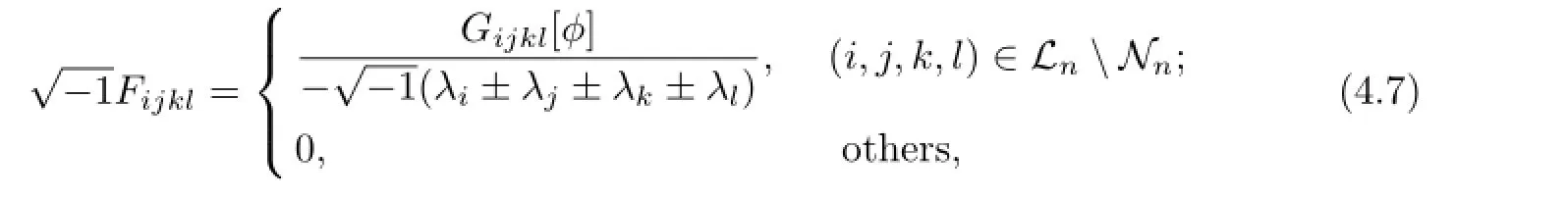
and
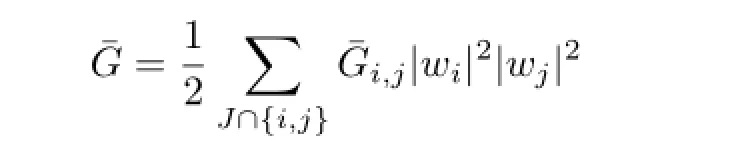
with coefficients
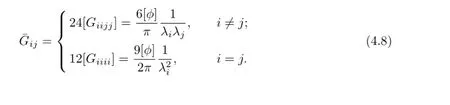
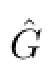
is independent of{wj}j/∈J.Hence,we have
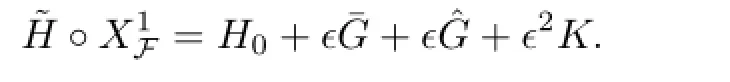
In the following,we introduce action-angle(θ,I)which satisfies
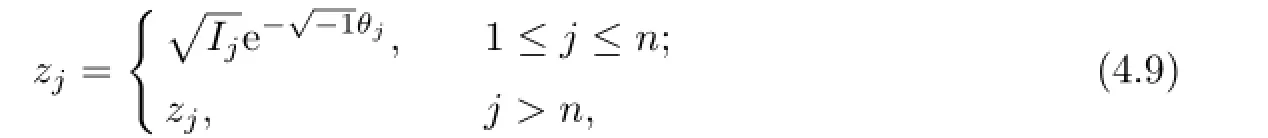
By symplectic transformation,the normal form can be transformed into
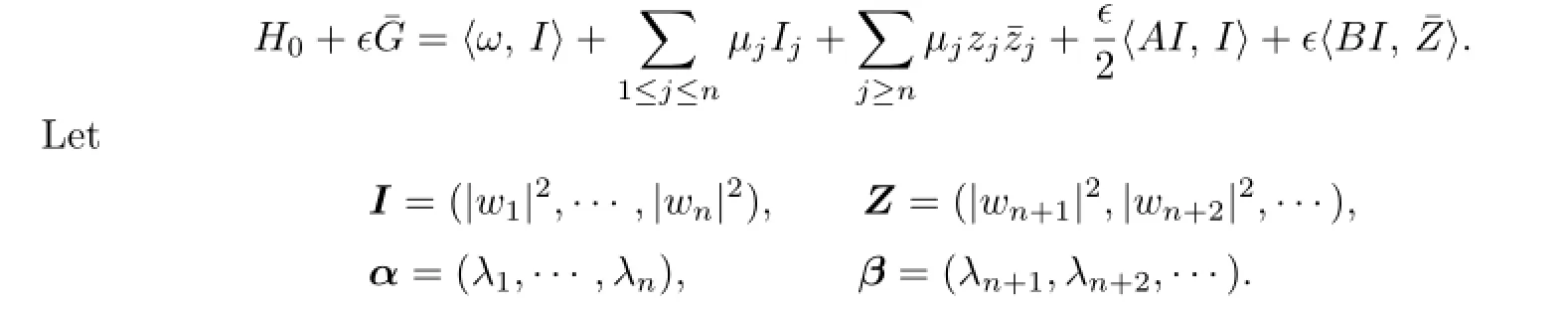
By Proposition 4.1,we obtain


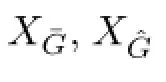
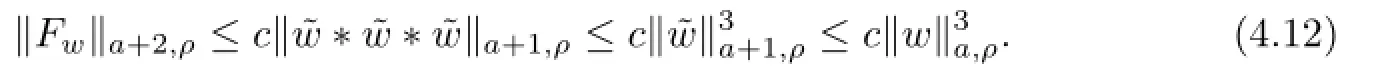
It follows from(4.12)that in a sufficiently small neighborhood of the origin in la,ρ,the time 1-map is well defined and gives rise to a real analytic,symplectic change with the estimates. Since
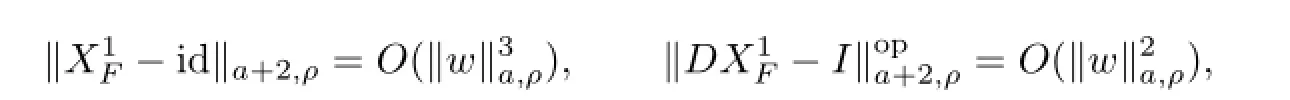
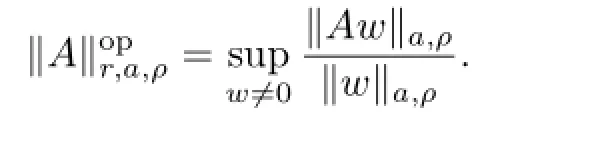
Obviously,
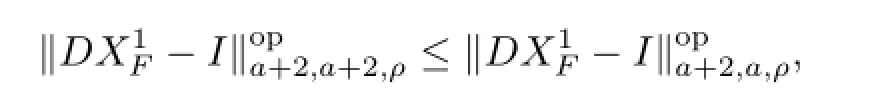
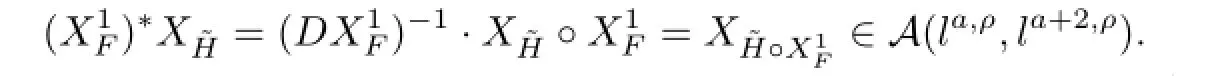
For Lie bracket,it also holds.These two facts show that XK∈A(la,ρ,la+2,ρ),the same hold for X¯G,XˆG∈A(la,ρ,la+2,ρ).
Next,in order to prove our main result,we need to the infinite dimensional KAM theorem,which was first proved by P¨oschel[7],so we should estimate three conditions.
Non-degeneracy:Since A is reversible,the map ξ-→ω(ξ)is Lipschitz between Rnand its image.Moreover,for all integer〈l,β〉/=O,1≤|l|≤2.When ξ is sufficient small enough,Bξ is sufficient small also,hence〈l,Ω(ξ)〉/=O,1≤|l|≤2.
Spectral asymptotic and the Lipschitz property:Since
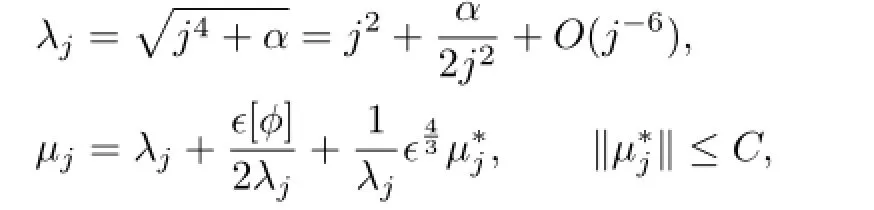

Base on[9],by using infinite dimensional KAM theorem,the Theorem 2.1 can be proved.
References
[1]Johnson R A,Sell G R.Smoothness of spectral subbundles and reducibility of quasi-periodic linear differential systems.J.Differential Equations.1981,41:262-288.
[2]Coppel W A.Pseudo-autonomous linear equation.Bull.Austral.Math.Soc.,1977,16:61-65.
[3]Bogolyubov N N,Mitropolskii J A,Samoilenko A M.Methods of Accelerated Convergence in Nonlinear Mechanics.New York:Springer,1976.
[4]Dinaburg E I,Sinai Y G.The one dimensional Schr¨odinger equation with a quasi-periodic potential.Funct.Anal.Appl.,1975,9:8-21.
[5]Eliasson H L,Kuksin S B.On reducibility of Schr¨odinger equations with quasiperiodic in time potentials.Commun.Math.Phys.,2OO9,286:125-135.
[6]Chierchia L,You J G.KAM tori for 1D nonlinear wave equation with periodic boundary conditions.Commun.Math.Phys.,2OOO,211:497-525.
[7]P¨oschel J.A KAM-theorem for some nonlinear partial differential equations.Ann.Sc.Norm. Super.Pisa CI.Sci.(5),1996,23:119-148.
[8]Geng J S,You J G.KAM tori of hamiltonian perturbations of 1D linear beam equations.J. Math.Anal.Appl.,2OO3,277:1O4-121.
[9]Li Y,Yi Y.Persistence of lower-dimensional tori of general types in Hamiltonian systens.Trans. Amer.Math.Soc.,2OO5,357:1565-16OO.
1O.13447/j.1674-5647.2O16.O4.O1
date:April 7,2010.
The Science Research Plan(Jijiaokehezi[2016]166)of Jilin Province Education Department During the 13th Five-Year Period and the Science Research Starting Foundation(2015023)of Jilin Agricultural University.
E-mail address:changjing81@126.com(Chang J).
Communicated by Li Yong
杂志排行
Communications in Mathematical Research的其它文章
- Fock-Sobolev Spaces and Weighted Composition Operators among Them
- A Remark on Adaptive Decomposition for Nonlinear Time-frequency Analysis
- Bayesian Estimation for the Order of INAR(q)Model
- The Twin Domination Number of Strong Product of Digraphs
- A Generalization of Gorenstein Injective and Flat Modules
- Two Optimal Inequalities Related to the S´andor-Yang Type Meanand One-parameter Mean
