重力异常物性正则化反演研究
2016-11-18周宇轩
周宇轩, 雷 宛
(成都理工大学 地球物理学院,成都 610059)
重力异常物性正则化反演研究
周宇轩, 雷 宛
(成都理工大学 地球物理学院,成都 610059)
经典位场物性反演是建立在数与模型之间的线性关系,利用离散正演公式将每个剖分单元相对观测点的核函数进行计算,以寻求观测数据与核函数有最好的相关性。该类方法在计算过程最大的问题就是在解巨大超定方程组时,导致求解极不稳定。在前人的研究基础上,提出一种基于先验密度模型约束正则化条件下的重力异常视密度求解方法,通过L曲线法选取最佳的参数,使求解过程中有较高的稳定性和求解精度。这里以一理论模型作为观测数据,并引入噪声作为观测误差,通过算法的对比表明,该方法有很高的计算精度和稳定性,对于需要求解大型超定矩阵的三维模型,在给定先验初始模型的条件下,该方法仍然能够取得很好的效果。
重力异常; 视密度; 正则化; 先验模型; 约束反演
0 引言
重力勘探是地球物理勘探的主要分支之一。目前国内主要通过地面测量来获取研究区各点重力场观测值,再通过必要地改正得到重力异常值[1]。重力勘探方法作为重要的勘探手段,已经广泛应用于油气勘探、金属矿勘查、地质填图及工程与环境地球物理勘探等领域。随着仪器、计算机、导航定位等技术的不断发展,重力探测技术应用已经扩展到卫星、航空、海洋等方面。相应地,针对卫星、航空、海洋重力实际资料大面积、大数据量以及快速估算解释的要求[2],三维正反演也逐渐地发展起来。
反演是重力资料定量解释中的重要环节之一[3]。与其他地球物理方法一样,重力资料解释的目的在于通过地面或航空等实测数据利用某种手段推算出地下的密度分布规律,从而达到寻找目标地质体、推断地质体埋深和地质体分布范围的目的。虽然能很容易找到满足数据拟合空间的解模型,但是由于重力场的体积效应、有限观测数据的不准确性及反演问题的欠定性等几种因素的存在,反演结果往往产生多解性,从而很难得到一个符合实际情况的解。这就需要在反演过程中添加一些约束条件及先验信息,最大限度地保证反演结果的正确性,如王薇等[4]提出的地震波形反演的稀疏约束正则化方法;舒梦埕等[5]提出储层重力密度反演后验约束正则化方法等;Tikhonov[6-7]正则化算法使反演结果更加可靠。对于反演模型可用场源目标体的形状或遍历地下半空间的物性值大小来表示,这就产生了两种完全不同的反演方法:①几何反演;②物性反演。几何反演是在地下半空间场源体给定物性参数大小的基础上,利用地面观测异常来拟合几何体(如多边形或多面体)形状大小,通过几何体的形状大小来模拟目标体的分布规律。物性反演是将观测区域地下半空间离散化成规则的网格单元,通过反演方法确定各离散单元的物性值,由物性的分布确定场源的实际分布情况。早期以形态反演为主,主要应用于沉积基底界面反演以及形态简单的场源体反演等。随着计算机计算能力地提高,物性反演后来居上且从二维发展为三维,逐渐成为国内、外重力反演的主要方向[8]。
1 密度模型正演原理
建立如图1所示的二维密度模型和观测系统,在地表(z=0)处观测和接收数据,d(i)为在地面第i个观测点所得的数据,mj为地下介质剖分后第j个 单元的密度(通常是未知的)。

图1 密度模型及观测系统示意图Fig.1 Schematic diagram of density model and observation system
根据图1的重力观测模式,d(i)与mj的定量关系如式(1)所示。
d(1)=f1,1m1+f1,2m2+f1,3m3…+f1,mmm
(1)
其中:f1,j为重力场观测网格化后物理的距离函数。
剖分矩形截面重力正演公式,如式(2)所示。
(2)
其中:dx、dy分别为地下网格的长度和宽度;xk,zk为地下观测点坐标;G表示牛顿万有引力常数。
为了与实际重力异常相结合,此处计算的是每一个场源的引力在铅垂方向上的投影,最后将它们相加。需要计算一条测线上面的重力异常值,可以用式(3)的矩阵表示。
(3)
式(3)可以化简为式(4):
F m=d
(4)
其中:F为表示表示观测点与场源的核函数;m为每个网格单元的密度值;d为测线上面的重力异常观测值。
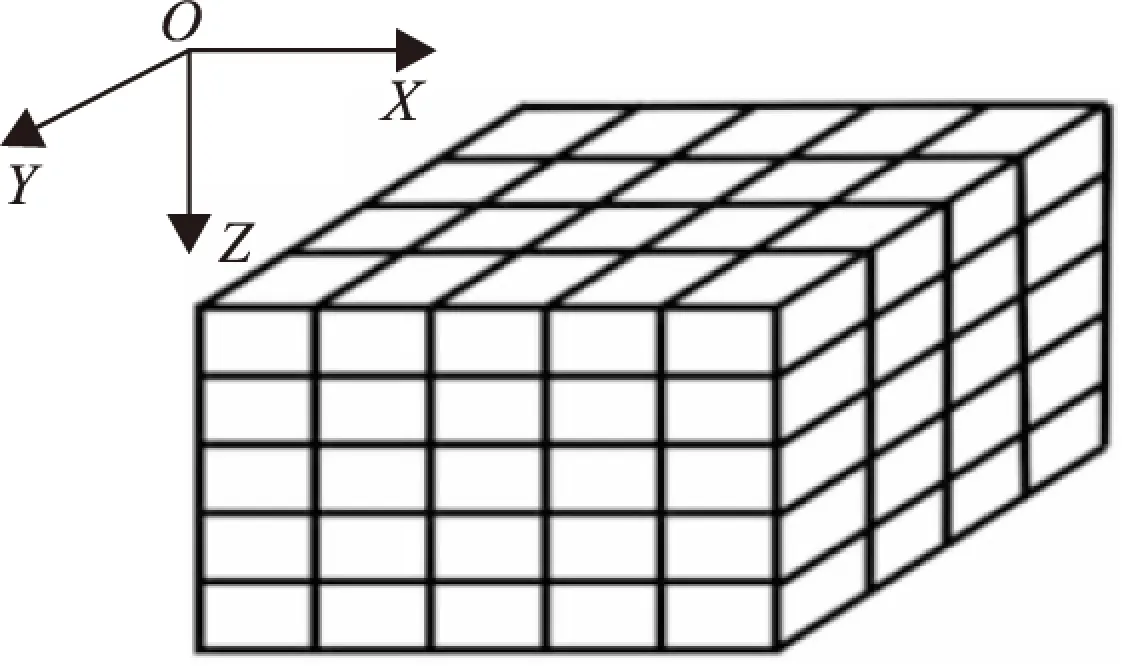
图2 三维密度模型和观测系统Fig.2 3D density model and observation system
三维模型通常将地下的地质体划分为多个立方单元体,密度模型和观测系统如图2所示。剖分立方体正演公式,如式(5)所示。
Δg= -G m|||[ξ ln(η+ρ)+
(5)
其中:η、ζ、ξ为网格单元的x、y、z坐标值;ρ为观测点到单元网格的距离,其表达式如式(6)所示。
(6)
若F等于式(7)所示的公式:
(7)
则可以将式(5)表示为:Δg=F m,为每个网格单元体的密度值。
2 正则化反演原理
在反演过程中,正演拟合参与运算的剖分单元数往往大于观测数据个数,特别是实际观测数据总是存在观测误差,导致反算F方程通常是一个超定矩阵,无法稳定线性的求出精确的解,为了使解更加稳定、准确,一般需要求解一个最小二乘意义下的近似解式(8)。
‖F m-d‖2→min
(8)
最小二乘本质是线性增量修正,由于修正量与解的收敛不确定性,导致求到的解会出现由稳定收敛到逐步发散的现象,为克服上述问题,作者运用Tikhonov正则化思想设计的正则化反演模型:

(9)
其中:α是正则化参数;m0为先验的密度模型;通过L曲线法选取最佳的α参数。
为降低反演的多解性,需要加入一个先验模型的约束。具体求解过程推导如下:
(10)
利用最小二乘原理将上诉问题转化为正则方程,得到的结果如式(11)所示。
(GTG+α2I)m=GTd+α2Im0
(GTG+α2I)(m-m0)=GT(d-Gm0)
(11)
令m*=m-m0,d*=d-Gm0,将其代入式(11)中,则可得到式(12)。
(GTG+α2I)m*=GTd*
(12)
求解上述方程,对矩阵G进行奇异值(SVD)分解:
(VSTUTUSVT+α2I)m*=VSTUTd*
(VSTSVT+α2I)m*=VSTUTd*
假设x*=VTm*,m=Vx,VVT=I
则有:
(STS+α2I)x*=STUTd*
(13)
从而可求到:
(14)
令m-m0=m*=Vx*,d=d*+Gm0,代入式(14),可以得到:
(15)
其中:S、U、V由矩阵G的SVD分解得到;Gm0、m0都是已知量,因此,作者采用L-curve曲线方法[9](图3)求解。
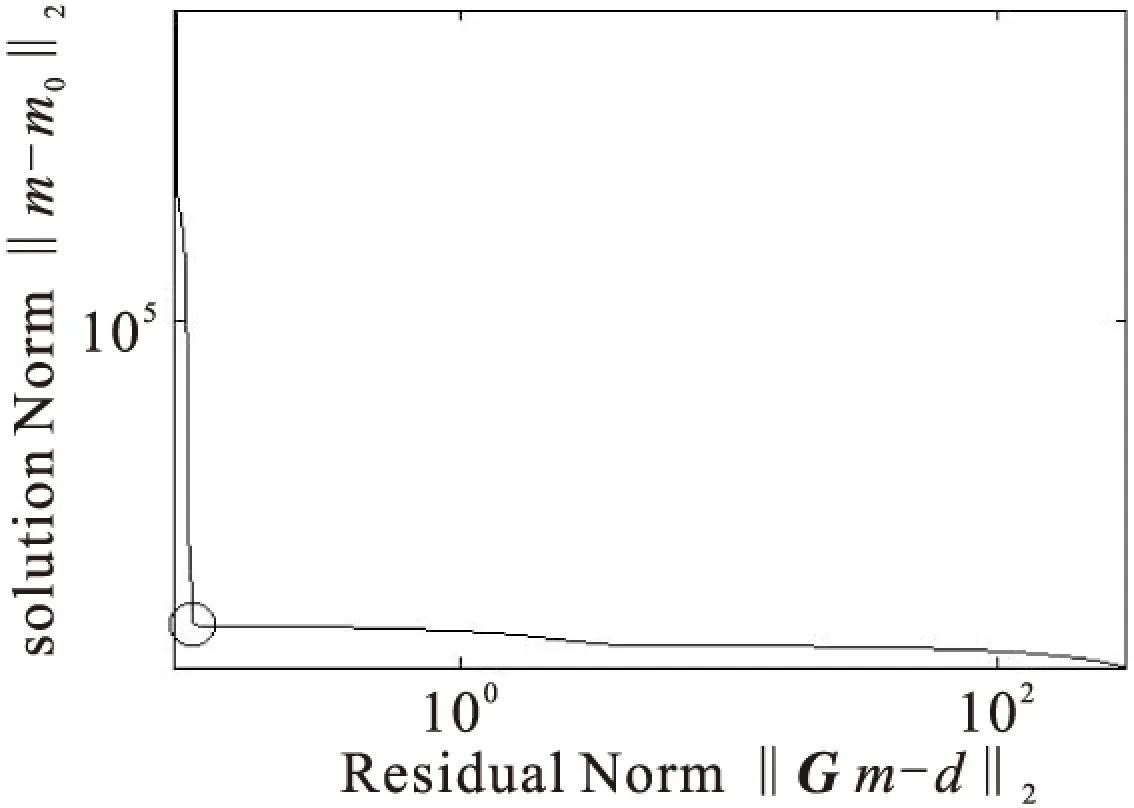
图3 L-curve曲线Fig.3 L-curve curve
正则化参数α的取值规则是从小取到大,依次用不同α算出的‖G m-d‖、‖m-m0‖取对数显示成L曲线。通过L曲线可以看出,当α很小时‖G m-d‖的值较小,而‖m-m0‖较大,这说明取较小的α时数据拟合效果较好,但反演结果与初始后验模型相比扰动较大。当α取较大时拟合误差‖G m-d‖变大,而反演结果与后验模型的距离‖m-m0‖变小。因此选择L曲线曲率最大处作为最优有α参数,这样既能平衡拟合误差,又能兼顾后验模型[10-12]。
求出α以后,代入到公式(15)中,即可求出m。
3 数值试验
设计一个二维模型(图4),其参数设置为:中间方形的密度为ρ=2 g/cm3,旁侧的密度设为 g/cm3;长宽分别为300 m、300 m,中心埋深为500 m;数据网格为10 m×20 m,测线上的数据点采样为2 000个,计算重力正演异常(图5)。
为模拟观测数据的随机观测误差,对该重力异常进行随机噪声添加(图6)。
对图6所得重力异常数据进行最小二乘优化反演,得到结果如图7所示,反演的视密度比较接近真实值2,但从视密度成像几何分布特征来看,与设计理论模型图4存在很明显的差异。在给定先验密度模型约束条件下,采用正则化方法,对含噪声重力异常数据进行反演,其视密度成像结果如图8所示。从图8中可以看出,无论密度反演值还是密度分布成像特征,均较最小二乘法有很好的改进,与设计模型(图4)有很好的对比性,表明基于正则化条件下的视密度反演算法,在噪声条件下,反演解未陷于局部收敛,其解有很高的稳定性和求解精度。
图5 正演重力异常Fig.5 Positive gravity anomaly

图6 加噪音正演重力异常Fig.6 Positive gravity anomaly with noise
将上述算法推广到三维模型,设计如图9的模型,其中模型密度为ρ=2 g/cm3,围岩密度为ρ=0.4 g/cm3;长、宽、高分别为300 m、300 m、300 m,中心埋深为500 m;数据网格为10 m×10 m×10 m,数据节点为1 000个;观测面数据采样为50×50=2 500个;其正演重力异常见图10。 设置如图11所示的先验初始模型,采用该先验模型进行正则化条件下的重力异常数据三维物性反演,得到的结果如图12所示。从图12中可以看出,反演的视密度大小及几何形状分布与图9有很高的吻合度。对比二维和三维反演的计算效率(表1)。
由表1可以看出,三维正则化物性反演虽然在迭代时间上消耗较多,但迭代次数相对二维反演较小,且能达到同等的效果。表明该方法在三维大型数据运算中仍具有很高的求解精度和稳定的求算解。

图7 最小二乘算法反演结果Fig.7 Least square algorithm inversion results

图8 加噪音正则化算法反演结果Fig.8 Inversion results with noise

图9 三维正演模型Fig.9 3D forward modeling

图10 三维正演平面图Fig.10 3D positive results plan

图11 先验初始模型Fig.11 A priori initial model

图12 反演结果Fig.12 Inversion results

网格点数迭代次数时间消耗二维反演10*20150.34三维正则化反演10*10*10100.53
4 结论
1)重力异常物性反演在解巨大超定方程组时,导致求解极不稳定,作者提出基于正则化条件下的约束反演,对于解决这类问题有很好的效果。
2)二维噪声模型和三维密度模型数值模拟结果表明,基于正则化条件下的反演算法,特别是在给定先验初始密度模型约束条件下,在求解的精度和求解的稳定性有其相对优势。
[1] GROETSCH C W. Inverse Problems[M]. Washington: The Mathematical Association of America, 1999.
[2] 陈召曦,孟小红,郭良辉.重磁数据三维物性反演方法进展[J].地球物理学进展,2012,27(12):503-511.
CHEN Z X, MENG X H, GUO L H. Review of 3D property inversion of gravity and magneticdata[J]. 2012,27(12):503-511.(In Chinese)
[3] 陈桂廷,罗强,周宇轩,等.三维位场正则化向下延拓成像技术[J].科技创新导报,2014(26):46-47.
CHEN G T, LUO Q, ZHOU Y X ,et al.Down-ward extension imaging techn ique of threedimensional potential field[J]. Scienc Science and Technology Innovation Herald,2014(26):46-47. (In Chinese)
[4] 肖庭延. 反问题的数值解法[M]. 北京:科学出版社, 2003.
XIAO T Y.Numerical solution of the inverse problem[M].Beijing:Science Press, 2003. (In Chinese)
[5] 舒梦埕,王彦飞.储层重力密度反演后验约束正则化方法[J].地球物理学,2015,58(6):2079-2086.SHU M C,WANG Y F.The posterior constrained regularization method for reservoirdensity inversion[J].ActaGeophysicaSinica,2015,58(6):2079-2086.(In Chinese)
[6] 徐新禹,李建成,王正涛,等.Tiknohov正则化方法在GOCE重力场中的模拟研究[J].测绘学报,2010,39(5):466-470.
XU X Y, LI J C, WANG Z T, et al.The simulation research on the Tikhonov regularization applied in Gravity Field[J].Acta Geodaeticaet Cartograph-icaSinica, 2010,39(5):466-470. (In Chinese)
[7] 傅初黎,洪芳,向团.不适定问题的Tikhonov正则化方法[J].计算数学,2006,28(3):237-246.
FU C L,HONG F,XIANG T.Iterated Tikhonov regularization for ill-poseproblems[J].Mathematica Numerica Sinica,2006,28(3):237-246.(In Chinese)
[8] 王邦华,王理.重磁位场的正则化向下延拓[J].物探化探计算技术,1998,20(1):30-35.
WANG B H. WANG L.A new normalized thod of down ward extrapolation for potential field[J]. Computing Techniques for Geophysical and Geochemical Exploration,1998,20(1):30-35. (In Chinese)
[9] TVEITO A, LANGTANGEN H P, NIELSEN B F,et al. Parameter estimation and Inverse problems[M].Pittsburgh:Academix Press,2013.
[10]冯宝宾. 不适定问题的正则化解算方法设计及应用[D]. 成都:成都理工大学, 2010.
FENG B B.Design and application of theregularization method for solving ill posed problems[D].Chengdu:Chengdu University of Technology,2010.(In Chinese)
[11]ARSENIN, IA. V. Solutions of ill-posed problems [M]. Washington:Winston,1977.
[12]刘银萍,王祝文,杜晓娟,等. 基于Tikhonov正则化算法的重力数据三维约束反演[J]. 地球物理学报, 2013, 56(5):1650-1659.
LIU Y P, WANG Z W, DU X J, et al. 3D constrained inversion of gravity data based on Tikhonov regularization algorithm[J].Chinese Journal Geophysics,2013,56(5):1650-1659. (In Chinese)
Study on physical properties regularization inversion of gravity anomaly
ZHOU Yu-xuan, LEI Wan
(College of Geophysics,Chengdu University of Technology,Chengdu 610059,China)
Classical potential field physical properties inversion is based on the linear relationship between the number and the model.We calculate each cross-sectional unit relative to observation point kernel function by using discrete forward formula to seek the best correlation in the observational data and the kernel function. The biggest problem of this kind of method calculation is unstable system to solving when we solve the large set of equations. On the basis of previous research,a kind of density algorithm is put forward based on the prior density model regularization constraint conditions of gravity anomaly in this study.The solution process has high stability and accuracy by using the L-curve method to select optimal parameters. In this paper,we establish a theoretical model as the observation data and introduce a noise as the observation error.Calculation results show that the method has high accuracy and stability through the comparison of different algorithms.Given a priori model of the initial conditions,the method can still achieve good results for the need for solving large over determined matrix of 3D model.
gravity anomaly; apparent density; regularization; a priori model; constrained inversion
2016-04-13 改回日期:2016-06-14
中国地质调查项目(12130113095100)
周宇轩(1992-),男,硕士,从事地球物理勘探方法研究,E-mail:zhouyuxuan@163.com。
1001-1749(2016)05-0579-05
P 631.1
A
10.3969/j.issn.1001-1749.2016.05.01
