气力提升理论模型建立及验证

胡 东, 王晓川, 唐川林, 康 勇



气力提升理论模型建立及验证

胡 东1,2, 王晓川1, 唐川林2, 康 勇1

(1. 武汉大学水射流理论与新技术湖北省重点实验室, 武汉大学动力与机械学院, 湖北武汉 430072; 2. 湖南工业大学水射流研究所, 湖南 株洲 412007)

气力提升技术已成功应用于深井取水、石油开采及危险介质输送等领域，其系统常规特性已得到较为深入的分析，然而针对于此的理论模型研究却涉猎较少。基于动量定理，并结合压强梯度损失模型建立适用于液体输送的气力提升理论模型，从而数值计算得出液体表观速度随系统结构及运行参数的变化规律，并通过对小型气力提升系统的实验结果分析验证理论模型的可靠性。结果表明，存在一最佳气体表观速度使得液体表观速度达到最高，且峰值位置随浸入深度升高向低气体表观速度偏移。液体表观速度随管径增加在跨过其临界点之后亦出现先升后降之趋势，峰值点随气体体积流量增加表现出右移特征。在临界浸入深度之上，液体表观速度随其升高而上扬，且随气体流量降低曲线凹凸程度显著增加。此外，进气口位置下移有助于气力提升性能的增强。在临界实测结果与计算值吻合度较高，为气力提升系统的设计提供了理论依据。

气力提升；动量定理；管径；浸入深度；进气口

1 前 言

气力提升装置是以压缩空气为工作介质,进行抽吸和压送液体的流体运输机械[1]。其内部不含运动部件,结构简单,已渐成为深井取水、石油提升及危险性化工液体输送有效而可靠的工具。

针对气力提升液体的研究，已进行了大量探索。这些研究主要集中在系统结构参数、运行参数的实验研究，管内流型识别以及理论模型的分析上。Kassab，Cho，Esen和Keng等[2~5]主要实验研究了气流量、浸入率、管径等基本参数影响气力提升性能的规律，提出了系统设计的经验模型，但缺乏必要的理论支持。Kumar，Hanafizadeh和Charalampos等[6~8]则是实测管内气含率及压力分布，获得了流型识别较为精确的方法，但同样未给出相应的理论模型。李霞和谢代梁等[9,10]也开展过类似研究。鉴于此，Hanafizaden和Wael等[11,12]基于分相流理论基础构建了气力提升系统理论模型，数值计算得出了含气率以及液体排量的变化规律，这对指导气力提升系统的设计不无裨益，但其模型建立及求解复杂，且受限于流型。 Mahrous[13]则基于动量定理并结合相关经验公式建立了垂直气液两相流理论模型，且将此应用于含有突扩管道的气力提升系统，取得了较佳的预测精度。但由于大量经验参数的引入，致使模型实用性受限于工况。笔者及课题组[14,15]则主要是对进气方式影响气力提升性能的机理及规律进行探讨，找出了较为合理的喷射器优化设计方案，并基于能量守恒原理获得了系统的无量纲模型。

迄今为止对于气力提升系统的模型分析多限于描述液流速度随气流速度的变化关系，而对管径、浸入深度以及进气口位置影响气力提升性能的研究涉猎极少。为寻求气力提升理论模型建立的新方法，基于动量定理，结合压强梯度损失模型建立管内混合流体的运动方程，旨在深入分析系统结构与运行参数对气力提升性能的影响机理及规律，并通过实验检验理论模型的可靠性。

2 理论建模

图1为气力提升模型，其中表示提升管轴向，为轴向压强，Pa；E和O分别指提升管底部及顶部，I为进气口。提升管内混合流体分为两段：单相水流(E至I)及气液两相混合流体(I至O)，两段分界面以进气口中心处横截面为准。

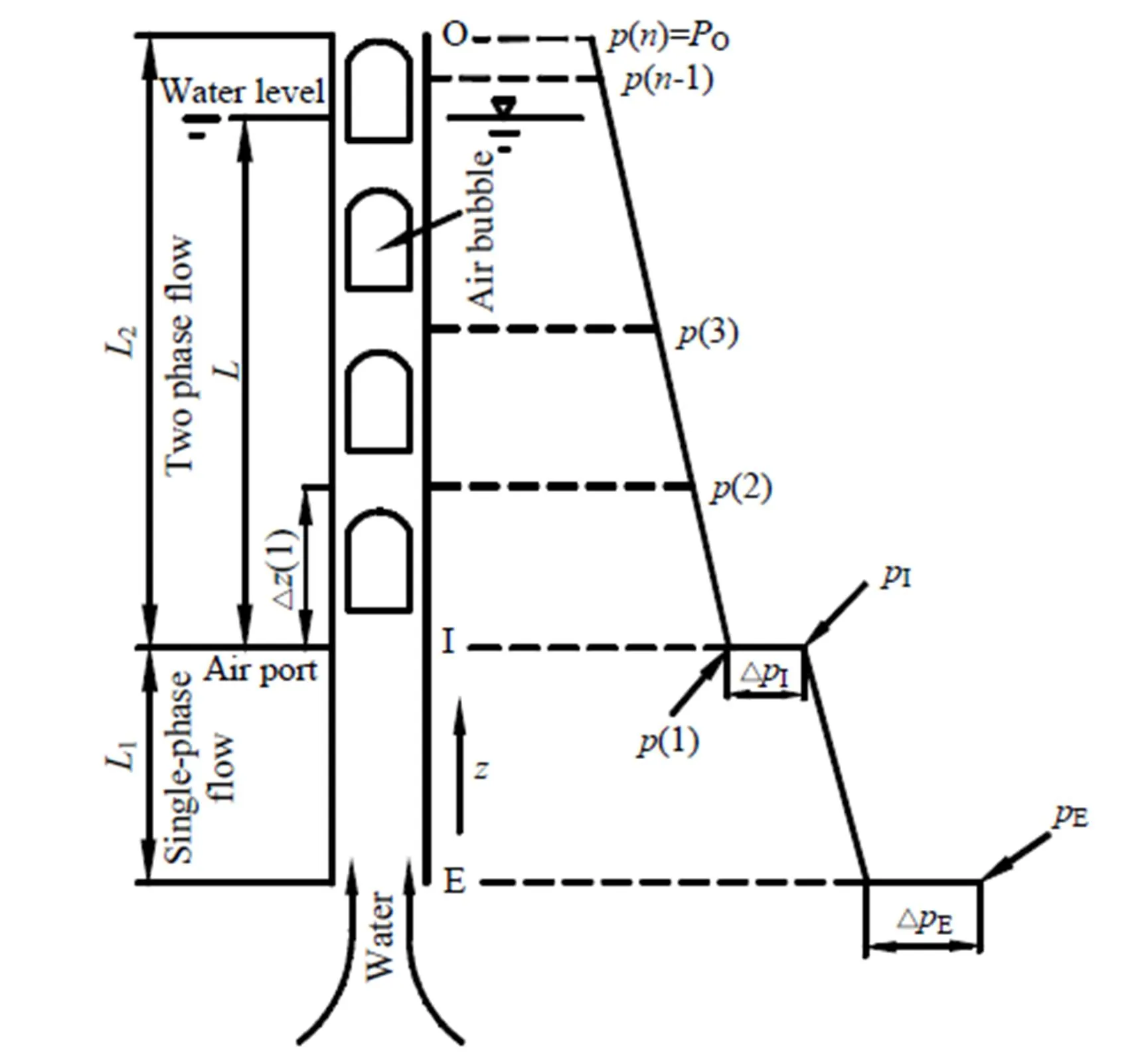
图1 气举装置模型简图及轴向压强分布图

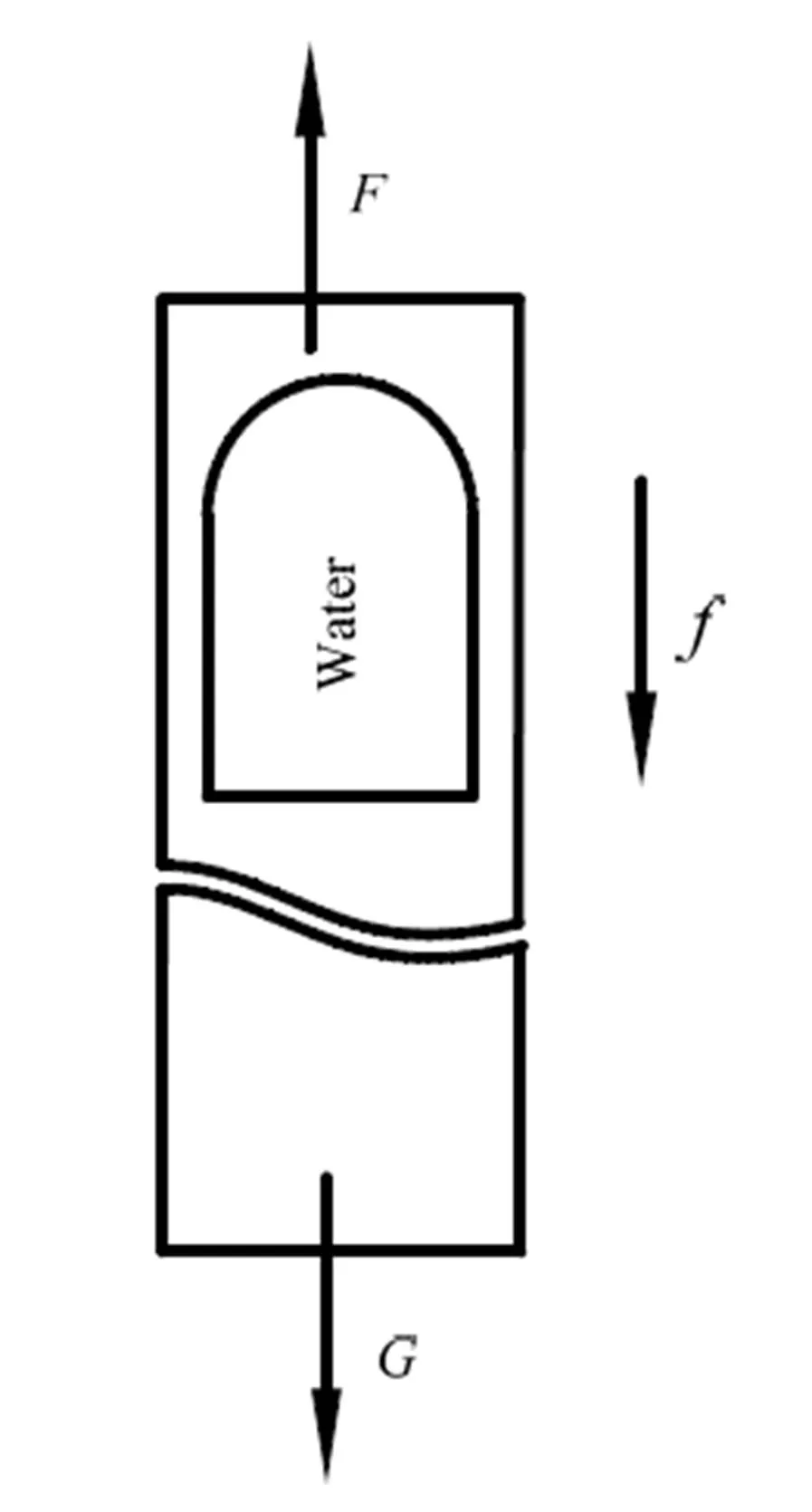
图2 控制体受力示意图

取管内混合流体E至O段为控制体，对其进行受力分析(如图2)，继而由动量定理可得：

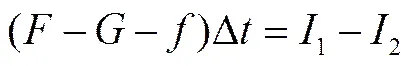
式中：为控制体底部所受水压力，N；为控制体重力，N；为管壁对控制体摩擦力，N；1，2分别为控制体流出断面和流入断面动量，kg×m×s-1；

各参量计算式如下：

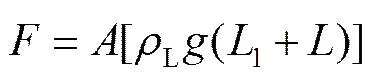
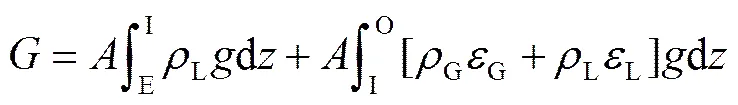
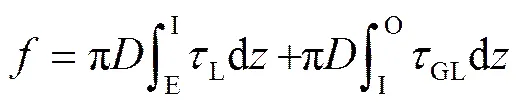
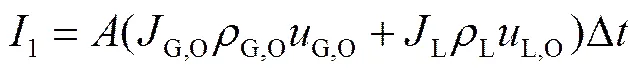
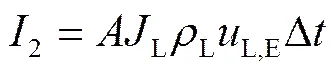
式中：下标G，L分别为气、液各相；GL指气-液两相；与分别为控制体横截面积(m2)与直径(m)；为密度，kg×m-3；为表观速度，指单位面积内流体的体积流量，m×s-1；为重力加速度，m×s-2；为速度，m×s-1；为摩擦剪切应力，Pa；为体积分数；1为提升管底部至进气口距离，m；2为进气口至提升管顶部距离，m；为进气口至水槽液面距离，m；为时间，s。

由此可得对控制体的总动量方程为

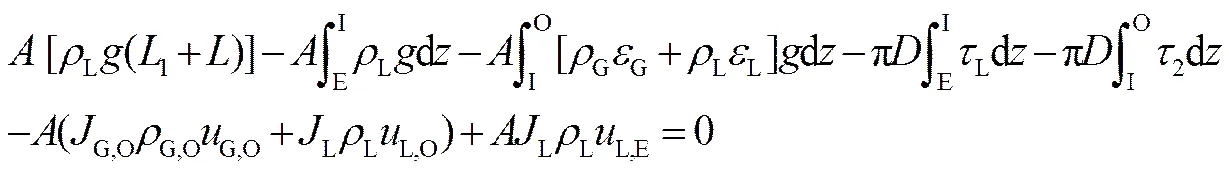
其中

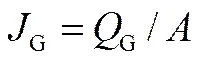
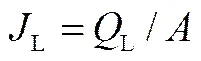
其中为体积流量，m3×s-1。

针对于气-液两相段，可以将其细分为段，再视相邻节点压强为线性变化，且各结点对应压强值分别定义为(1)，(2)，(3)，…，()，其中()=O≈0(0为标准大气压)，如图1所示。

式(2)第1项为提升管底部所受水压。第2项为单相段水流重力，其计算式如下

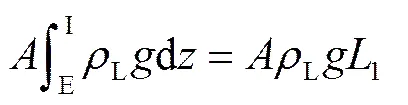
第3项表示两相段混合流体重力，视各段内流体物理性质一致，可得

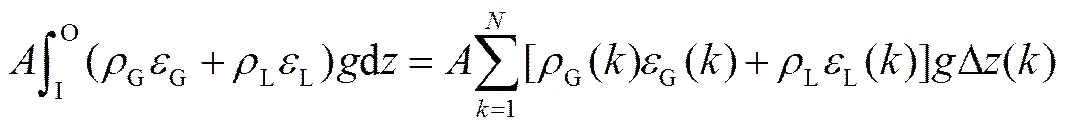
由于实验中提升管浸入段(≤1.05 m)较短，加之产生的水压远小于标准大气压，则可视管内气体在常温常压下变化。因此，在恒定进气量下可忽略管内气相密度与体积分数沿轴向的差异，则有

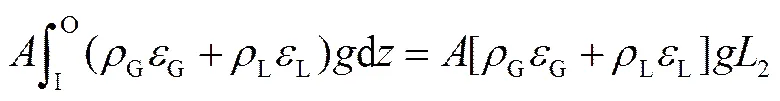
其中

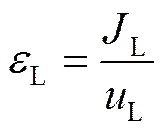
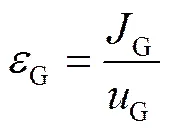
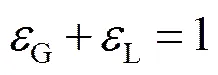
由此则式(6)则可改写为

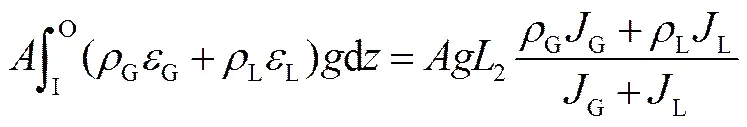
式(2)第4，5项分别为单相和两相段所受的管壁摩擦力。考虑摩擦阻力均转化为压降，则可得

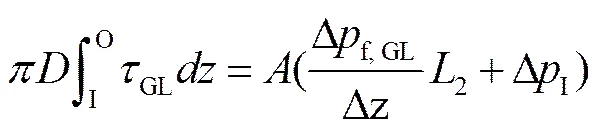
式中：Δf,L/Δ和Δf,GL/Δ分别为单相及两相段压强梯度损失，Pa×m-1；ΔE为控制体进口E处压强损失，包括沿程压强损失和局部压强损失；ΔI为进气口I处压强损失，即单相段末与两相段初始位置压强差值。

对单相段压强梯度损失Δf,L/Δ，其计算如下：

由计算L可知其处于4000~100000，则沿程阻力系数可按照布拉修斯公式计算，如下

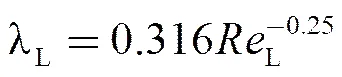
且

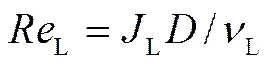
则式(14)改写为

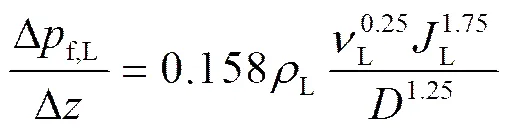
对Kassab等[16]所提出的理论模型进行修改，可计算得出气-液两相段内压强梯度损失(Δf,GL/Δ)，如下

搁浅成本：电力公司资产的市值与会计账簿上记载的资产价值(账面价值)之差。未来利润流的净值决定资产的市值。管制机构制定电价是基于资产会计账面值并保证合理利润回报，因此，在管制体制下，资产的市值应该接近于账面值。但是当电价由市场决定时，如果市场价格低于管制价格，原有资产的市值将贬值。

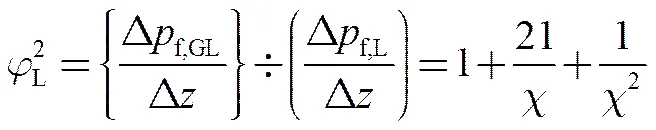
其中

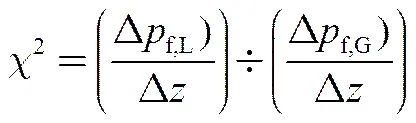
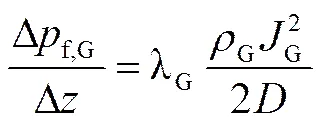
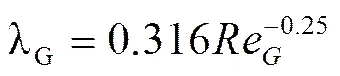
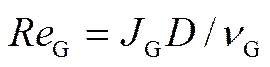
结合式(18)~(22)，最终可获得两相段压强梯度损失，如下

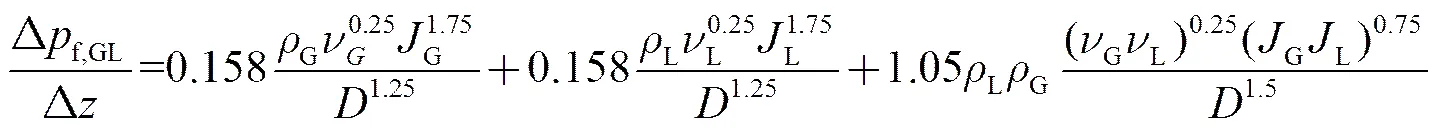
分析Liang等[17]所提出的压强损失模型，则可得式(12)与(13)中ΔE和ΔI的计算式，分别如下

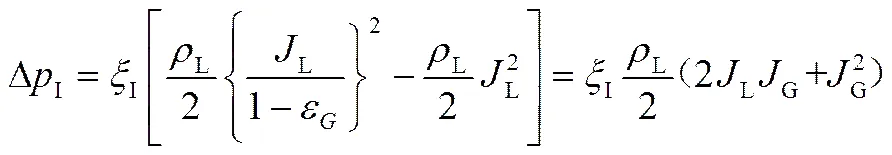
在计算式(2)第6，7项时，由于已忽略气相密度与体积分数沿轴向变化的差异，结合式(8)与(9)可得下式

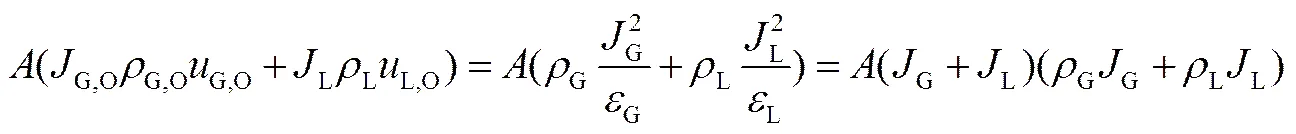
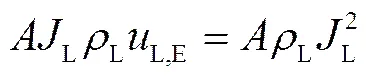
将式(3)~(26)代入式(2)，即可得气力提升系统理论模型，见下式

3 实验装置及方法

图3为气力提升性能测试装置示意图。考虑到空压机输出端气流因活塞往复运动易出现波动，在气体流量计前段设置一整流器降紊。为避免实验系统生锈，提升管与气力泵由不锈钢加工制成。空气经空压机增压后被送至气力泵与水混合，因两者密度差异而达到提升液体目的，并在进气口以下形成单相水流，而在其之上则发展成为气-液两相流。水槽液面位置由其底部阀门与进水管阀门控制。事实上，由于系统所排出的液体最终又返回至水槽，使得某工况下浸入深度()基本恒定，避免了频繁调节阀门所引发的浸入率波动问题。

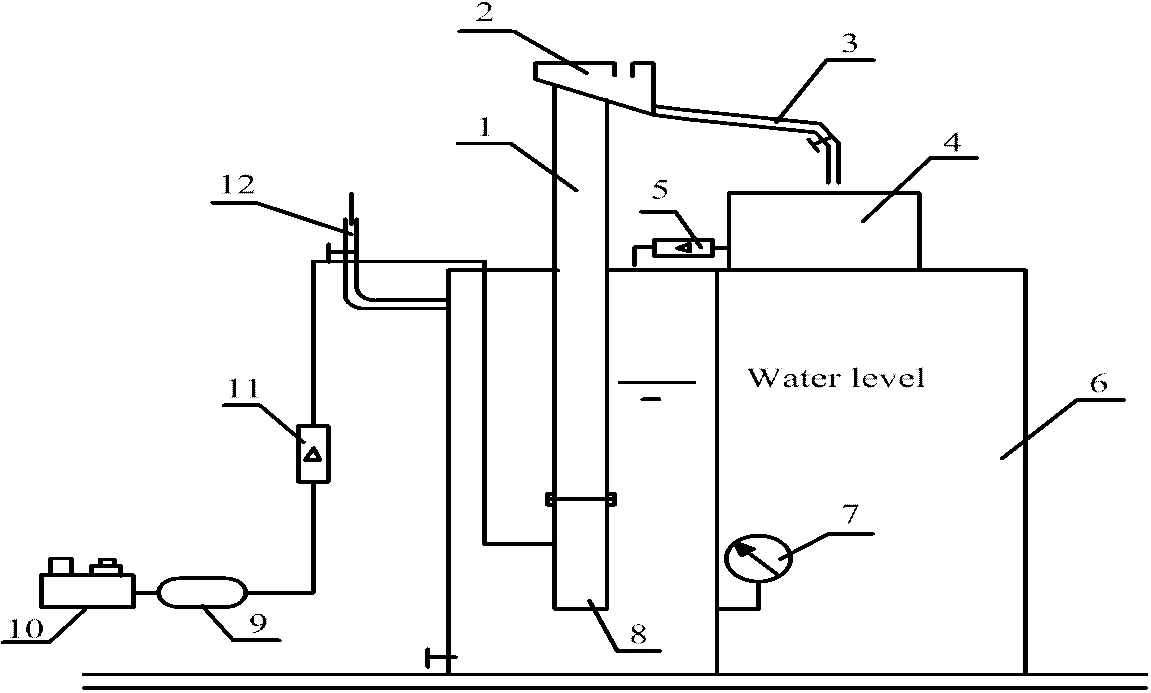
图3 实验系统示意图

1. riser 2.air separator 3.delivery pipe 4.storage water box 5.liquid flow meter 6.water reservoir 7.pressure gage 8.airlift pump 9.accumulator 10.air compressor 11.air flow meter 12.inflow pipe

为降低浸入深度因液面波动所引起的测试误差，在靠近液体流量计出口且与水槽顶部平齐处设置一与提升管内径相近的环形致密不锈钢网以减弱返回液体对槽内液体的冲击。同时，在水槽隔板上与气力泵底部同高度处安设一压力表(图3)以实现浸入深度的精确测量，其误差限制在±3%以内。另外，理论计算模型(式26)中所需参数可基于实验工况而得，如表1所示。

表1 实验系统参数

4 计算结果分析及其验证

图4为液体表观速度的计算与实测值的比较结果。从中可知，随气体表观速度增加，任一浸入深度下液体表观速度均首先快速增加，继而降至零。由此可判断气量值过低与过高均不利于气力提升。这与笔者之前对固体颗粒输送的研究结论基本一致[18]。事实上，随气量值上升，管内依次为泡状流、弹状流和环状流，且仅在弹状流条件下气力提升性能最优，由此可解释曲线存在峰值的原因。据图还可得出管内流型由泡状流迅速过渡至弹状流，而之后弹状流与团状流的转捩段则较长。这说明在实际应用中，少量的气流量即可使得气力提升性能达到最佳。

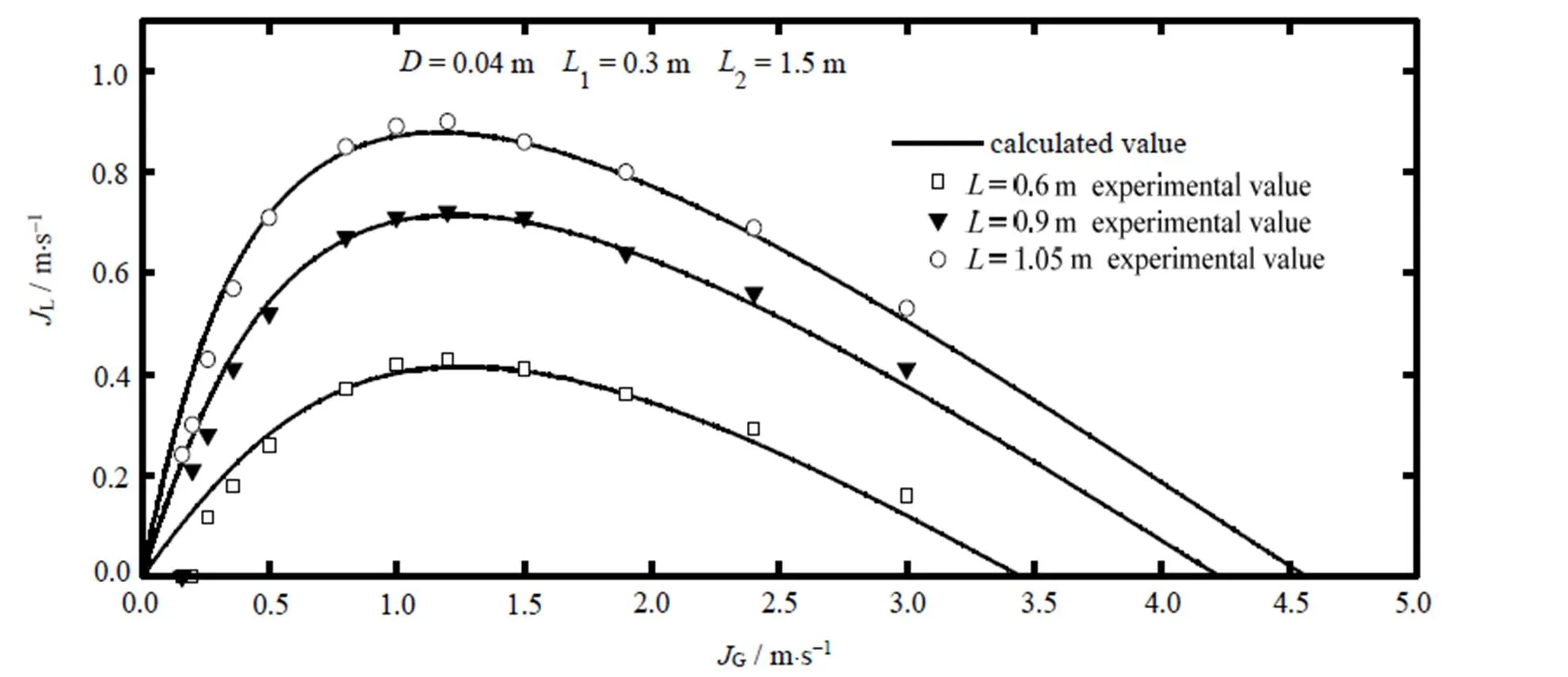
图4 液体表观速度随气体表观速度的变化关系

由图还可知，不同浸入深度下液体表观速度的峰值位置略有差异，且随浸入深度升高而向低表观气速偏移，在浸入深度分别为=0.6，0.9和1.05 m时，相应峰值则分位于G= 1.31，1.19和1.12 m×s-1。另外，极限气体表观速度(即L=0时对应的G,max)也因浸入深度增加相差较大，且依次为3.46，4.23和4.58 m×s-1。这说明浸入深度加大可拓宽有效气流范围(0~G,max)。分析其原因可能是由于浸入深度升高，管内气泡膨胀受抑，气芯范围缩小，引发环状流延迟所致。此外，比较图中计算与实测结果还发现，理论与实验值在临界气量(G,cri，实验输送水流的临界气量值)之上吻合程度较高，而之下则失效，其主要原因是在理论模型中未考虑微小气量值下气液两相滑移极大之事实。

液体表观速度随管径的计算结果如图5所示。从中可知，液体表观速度随管径加大快速增加至峰值后其下降趋势放缓，并逐渐趋于稳定。这说明气体体积流量恒定时，管径过小与过大均不利于气力输送，过小会引发管内阻力损失加剧，而过大则又会导致推动水流上升的气量不足。值得注意的是，只有当管径大于其临界值(即L=0时对应的min)气力提升才得以实现。而在临界值以内，一方面阻力损失增加，另一方面因进气口附近管道空间限制积压大量气体从而阻滞其下部流体上移，若管径太小甚至还会引发流体反向下移，在管底部外围形成上升流。实验过程中就观测到=0.004 m与G=0.0144 m3×s-1时提升管上端出现气喷而在管道外围液面形成泡流的特殊现象。由此可判断此时在气力泵底部发生了气体溢流。值得一提的是，实际工程应用时可利用该现象以有效解堵。

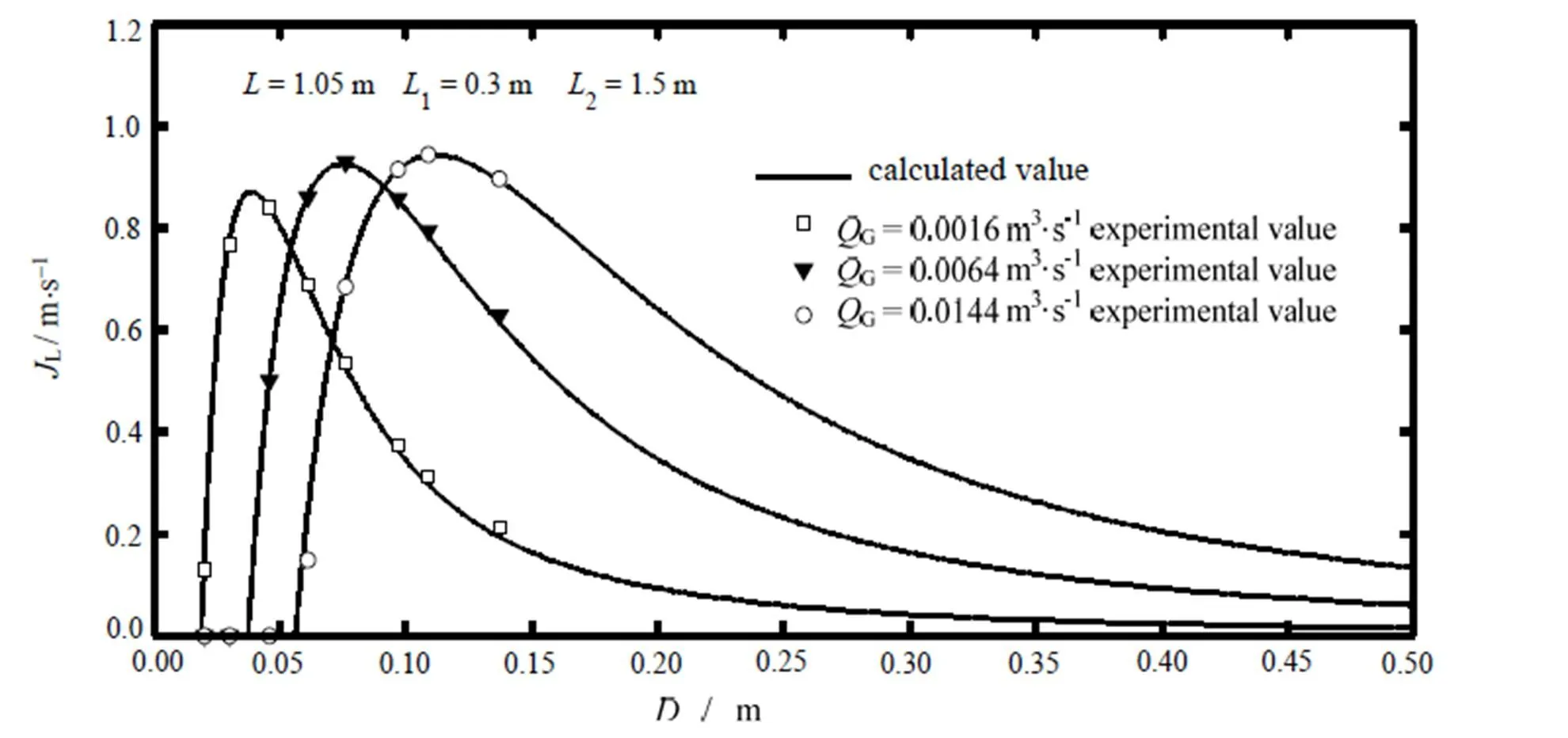
图5 液体表观速度随管径的变化关系

由图还可知，随进气口气体体积流量的增加，对应液体表观速度的峰值位置向更大管径偏移，对应G= 0.0016，0.0064和0.0144 m3×s-1，相应曲线峰值依次略有升高，其位置分别位于= 0.039，0.075和0.115 m处。由此可推，若气体体积流量升高，需增加管径以保持气力提升性能维持在最佳状态。此外，min也因G的升高而增加，液体表观速度的降幅因此则减小。据此可分析得出，小流量气体以小管径为宜，且合理管径范围较窄；而大流量气体则采用大管径为佳，且可用管径范围变宽。将计算与实测值比较可发现两者吻合程度在实测段尚佳，但在高管径下的计算值因条件限制缺乏实验佐证。

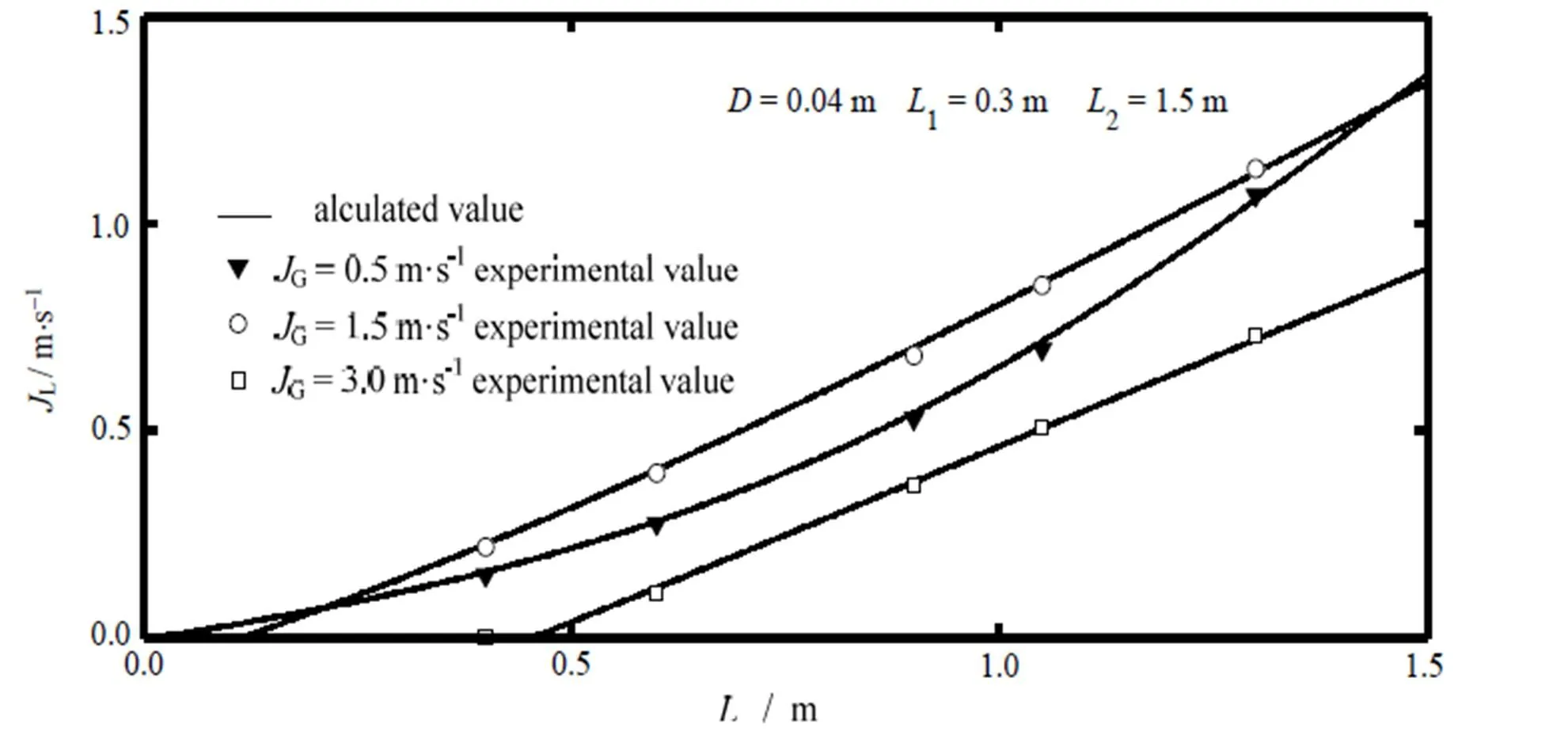
图6 液体表观速度随浸入深度的变化关系

图6反应了液体表观速度与浸入深度的变化关系。结果显示，只有当浸入深度跃过其临界值(L= 0时对应的min)后，液体表观速度才随其上扬。由此可见，对应0~min，液体因其自身重力水头(2-)过高而导致气力输送失效。据图分析可知，此时若降低气体表观流速，则min值左移，系统转而被“激活”。对应G= 0.5，1.5和3 m×s-1，min分别为0.01，0.12，0.46 m。结果说明气体表观速度越大，临界浸入深度愈高，液体"启动"则越难。据此可判断，气体进入管内与液体需经历一定管长完成混合，气量越高，所需混合段长度越长，否则易导致气体溢流，气力提升系统失效。

从图中还可知，气量值较高时(G=3 m×s-1)，液体表观速度随浸入深度变化近乎为线性升高，但随气量值降低逐渐转变为双曲线特征，且凹凸程度显著增加。可以预见，若图中G由0.5 m×s-1减小至一定值，则其曲线必与G= 3 m×s-1对应的曲线相交。结合上述分析可得，小气量虽对液体“启动”有优势，但在较高下则处于劣势，而在极高下(水槽液面与管出口端接近)却又有所反弹。

图7表示进气口位置对液体表观速度的影响规律。显然，当提升管总长及水槽液面恒定时，进气口位置上移(吸程段1增加)有碍于气力提升性能的增强。分析其原因，一方面是浸入深度降低所致，另一方面则因提升系统由扬程工作渐变为吸程运行引发阻力损失升高所引起。该结论也表明在应用气力提升系统时应以高扬程作用为宜。若继续增加1直至极限值1,max(此处L=0)，则气力提升系统失效，且气量值越小，对应1,max愈大，进气口位置变动范围也越大，但系统提升性能却未必提高。

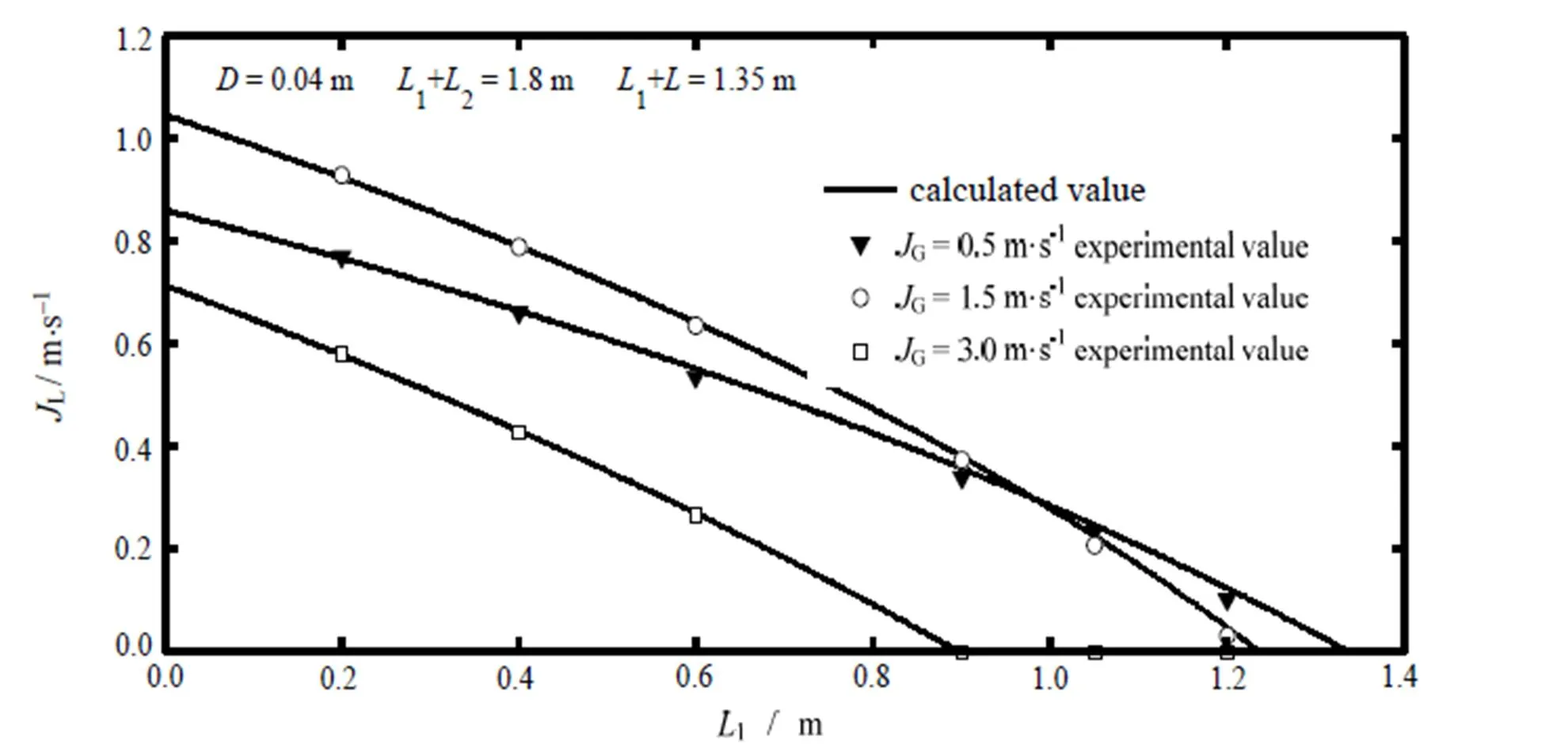
图7 液体表观速度随进气口位置的变化关系

比较不同气量值下曲线特征还可知，当吸程段1=0，三种工况中对应G=1.5 m×s-1时其液体表观速度最高，G= 3 m×s-1最低，由此可判断此处(1=0)应存在一最佳气量值使得气力提升性能最佳。而当进气口接近水槽液面位置时，应采用小气量输送以增强气-液间传质效果，并避免出现气体因混合段较短而直接排送至液面外的情况。此外，实测值与计算结果在吸程段较低时吻合度较高，但随此增加略有分离，这应是由气体溢流逐渐加大所致。

5 结 论

(1) 基于动量定理并结合压强梯度损失方程导出了低浸入率下适合于气-液输送的气力提升系统理论模型，并对其有效性进行了佐证，实测值与计算结果吻合较好。

(2) 存在一最佳气体表观速度使得液体表观速度达到最大值，且液体表观流速的峰值位置随浸入深度升高而左移。另外，极限气体表观速度也因浸入深度增加而升高。

(3) 当管径位于其临界值之下，气力提升系统失效，而之上则存在一最佳管径。液体表观速度峰值位置随气体体积流量增加而右移，临界管径也因其升高而增加。

(4) 只有当浸入深度跃过其临界值后，液体表观速度才随其上扬，且其临界值随气体表观速度减小而左移，相应曲线凹凸程度也显著增加。在浸入深度极低与极高时，应以小气量工作为宜。

(5) 进气口位置下移有助于气力提升性能的增强。当进气口接近水槽液面时，应以小气量为佳。

参考文献：

[1] Hanafizadeh P, Ghanbarzadeh S, Saidi M H. Visual technique for detection of gas-liquid two-phase flow regime in the airlift pump [J]. Journal of Petroleum Science and Engineering. 2011, 75(3): 327-335.

[2] Kassab S Z, Kandil H A, Warda H A,. Experimental and analytical investigations of airlift pumps operating in three-phase flow [J]. Chemical Engineering Journal, 2007, 131(1): 273-281.

[3] Cho N C, Hwang I J, Moon L C,. An experimental study on the airlift pump with air jet nozzle and booster pump [J]. Journal of Environmental Sciences Supplement, 2009, 21(1): S19 -S23.

[4] Esen I I. Experimental investigation of a rectangular airlift pump [J]. Advances in Civil Engineering, 2010, 11(1): 1-5.

[5] Keng W C, Malcolm M. Analysis and modelling of water based bubble pump at atmospheric pressure [J]. International Journal of Refrigeration, 2013, 36(5): 1521 -1528.

[6] Kumar E A, Kumar K R V, Ramayya A V. Augmentation of airlift pump performance with tapered upriser pipe-an experimental study[J]. Journal of the Institution of Engineers, 2003, 84 (3): 114-119.

[7] Hanafizadeh P, Saidi M H, Karimi A,. Effect of bubble size and angle of tapering upriser pipe on the performance of airlift pumps [J]. Particulate Science and Technology, 2010,28(4): 332-347.

[8] Charalampos T, Eeftherios G. Two-phase flow pattern transitions of short airlift pumps [J]. Journal of Hydraulic Research, 2010, 48(5):680-685.

[9] LI Xia (李霞), JI Hai-feng (冀海峰), WANG Bao-liang (王保良),. A novel method for oil-water two-phase plow measurement (油水两相流参数测量新方法研究) [J]. Journal of Chemical Engineering of Chinese Universities (高校化学工程学报), 2012, 26(5): 755-762.

[10] XIE Dai-liang(谢代梁), ZHU Yue(朱跃), XU Zhi-peng (徐志鹏),. Gas-liquid two-phase flow measurement using differential pressure signals from a dual-cone flowmeter (基于双锥流量计差压信号的气液两相流参数测量) [J]. Journal of Chemical Engineering of Chinese Universities (高校化学工程学报), 2015, 29(1): 84-89.

[11] Hanafizadeh P, Karimi A, Saidi M H. Effect of step geometry on the performance of the airlift pump [J]. International Journal of Fluid Mechanics Research, 2011, 38(5): 387-408.

[12] Wael H A, Hassan M B. Dual-injection airlift pumps: an enhanced performance [J]. Particulate Science and Technology, 2012, 30(6): 497-516.

[13] Mahrous A F. Airlift pump with a gradually enlarged segment in the riser tube [J]. Journal of Fluids Engineering, 2013, 135(3): 1-4.

[14] Hu D, Tang C L, Cai S P,. The effect of air injection method on the airlift pump performance [J]. Journal of Fluids Engineering, 2012, 134(11): 1-7.

[15] Tang C L, Hu D, Zhang F H. Effect of air injector on the airlift performance in air-water-solid three-phase flow [J]. Journal of Energy Engineering, 2014, 140(1): 1-8.

[16] Kassab S Z, Kandil H A, Warda H A. Air-lift pumps characteristics under two-phase flow conditions [J]. International Journal of Heat and Fluid Flow, 2009, 30(1): 88-98.

[17] Liang N K, Peng H K. A study of air-lift artificial upwelling[J]. Ocean Engineering, 2005, 32(5):731-745.

[18] HU Dong(胡东), TANG Chuan-lin(唐川林), ZHANG Feng-hua(张凤华),. Theoretical model and experimental research of airlift device in borehole hydraulic jet mining(钻孔水力开采用气力提升装置模型的建立及实验研究)[J]. Journal of China Coal Society(煤炭学报), 2012, 37 (3):522-527.

Modeling and Validation of an Airlift Lifting System

HU Dong1,2, WANG Xiao-chuan1, TANG Chuan-lin2, KANG Yong1

(1. Key Laboratory of Hubei Province for Water Jet Theory & New Technology, SchoolofPowerandMechanicalEngineering,Wuhan University, Wuhan 430072China;2. Modern Jetting Department, Hunan University of Technology, Zhuzhou 412007, China)

Airlift technology has been widely applied in areas of deeper water intaking, petroleum drilling and dangerous medium conveying. Conventional characterization has been deeply investigated, but studies on theoretical models are insufficient. A frictional pressure drop model together with a numerical model of airlift based on momentum theorem were combined to study water conveying to optimize geometrical and operational parameters of the airlift system. Furthermore, a small airlift system was set up for the verification of the theoretical model. The calculated results indicate that water superficial velocity increases with the volumetric flux of the injected air to a maximum value and then slightly decreases. The maximum value moves left with the increase of submerged length. The relation between water superficial velocity and pipe diameter also shows a similar trend when the pipe diameter exceeds a critical limit, and the maximum value moves right with the increase of air flow rate. The water superficial velocity increases with submerged length when the length exceeds a critical value, at which the curvature increases with the increase of air flow rate. In addition, the airlift performance can be enhanced by moving the air inlet downwards. The experimental results show good agreement with the proposed model, which provides theoretical support for developing airlift systems.

airlift; momentum theorem; pipe diameter; submerged length; air inlet

1003-9015(2016)05-1074-08

http://www.cnki.net/kcms/detail/33.1141.TQ.20160920.1621.002.html

TP69

A

10.3969/j.issn.1003-9015.2016.00.031

2015-04-24；

2015-08-04。网络出版时间：2016-09-20 16:21:48

国家自然科学基金项目(51374101)；国家重点基础研究发展计划(2014CB239203)；国家自然科学基金项目(51474158)。

胡东(1980-)，男，湖南溰县人，湖南工业大学讲师，博士。通讯联系人：王晓川，E-mail：hudong@126.com