岩石蠕变应变率与孔隙率相关性规律探析

◎ 袁靖周 广州航标处

岩石蠕变应变率与孔隙率相关性规律探析

◎ 袁靖周 广州航标处

通过分析岩石破坏过程中孔隙率变化规律，将其与蠕变过程中应变率变化规律联系起来，根据线性相关的假设导出了蠕变变形与孔隙率的关系式。本文基于孔隙率变化而建立的三阶段蠕变方程，为岩石蠕变模型研究提供了一个新的思路和方向。

岩石 孔隙率 蠕变 应变率

众所周知，岩石流变是岩石的一个重要力学特性，在岩石工程领域具有重要的理论和实际意义。但至今岩石的流变理论尚不成熟，许多问题亟待解决。从现有的岩石流变研究成果来看，大致可以分为以下几类：一是经验模型。根据岩石蠕变试验结果，由数理统计科学的回归拟合方法建立经验方程。经验公式的特点是简单实用，对特定的岩石而言，可以很好的吻合试验结果，但是这些公式是对具体的岩石试验得出的，因此对于其他类型岩石较难适用；二是元件模型。基本原理是按照岩石的弹性，塑性，粘性性质设定一些基本元件，然后根据具体的岩石性质将其组合成能反映各类岩石流变属性的本构模型。传统的粘弹性或粘塑性模型把时效变形完全归结为粘性效应，只对蠕变形态给予数学上的描述，并没有考虑岩石介质内在的物理力学性质，对导致流变破坏的损伤演化过程和细观力学机制缺乏认识。随着断裂力学，损伤力学的发展和完善，这些理论在岩石蠕变方面也取得了较多研究成果，如谢和平用损伤力学的方法建立了岩石的蠕变裂纹扩展模型。

本文另辟蹊径，从分析岩石破坏过程中孔隙率等基本物理性质变化入手，分析了孔隙率的变化规律。其次，根据岩石蠕变破坏过程中应变率变化特点与孔隙率之间的联系，根据假设建立了一种新的蠕变模型，旨为岩石蠕变研究提供一种新的思路。

1.岩石孔隙率变化规律分析

取岩石微元各边长度为 d x , d y , d z，其受载后各边长度为：

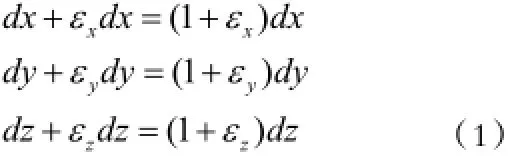
假定岩石中岩石材料在受载前后体积不可压缩，有：

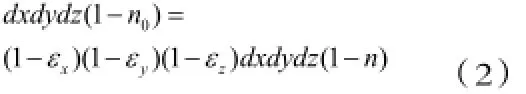
整理上式得：

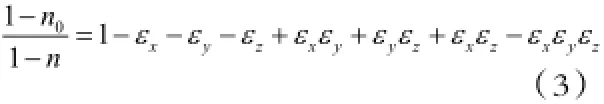
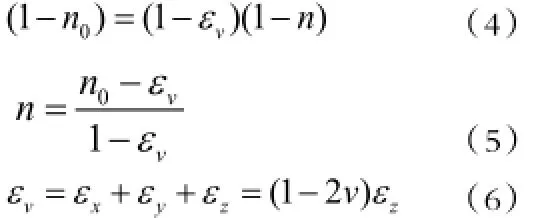
由于体积应变 εv< < 1，故（5）式又可改写为：

试验表明：对于弹性模量和泊松比为常数的岩石，其体积应变曲线可以分为三个阶段：（1）体积减小阶段此阶段内轴向应变为侧向应变，随着轴向应变的增加不断增加，体积逐渐减小。（2）体积不变阶段此阶段内在此阶段为0。（3）扩容阶段此时体积不断增加，侧向膨胀之和大于轴向应变，即开始出现负值。

于是，由（4）式可知，孔隙率在岩石破坏的过程中经过三个阶段的变化：先变小，然后保持不变，最后变大。孔隙率的变化是岩石的内在物理性质的变化，岩石蠕变破坏必然伴随着孔隙率的变化。

2.岩石蠕变破坏分析

典型的岩石蠕变破坏曲线包括三个阶段：稳态蠕变，等速蠕变，加速蠕变。对于稳态蠕变，其蠕变应变值随着时间有所增加，但蠕变的应变率是逐渐减小；当发展到等速蠕变时，其蠕变应变率保持不变；当蠕变进入加速蠕变时，蠕变应变率开始逐渐增大，直到破坏。

在岩石蠕变破坏过程中，首先岩石的蠕变应变率是逐渐减小，而岩石在蠕变过程中首先必定是岩石中的张开性结构面或微裂隙逐渐闭合，以致岩石的孔隙率减小，岩石被压密硬化，以致蠕变应变率随着孔隙率的减小而逐渐减小；当岩石被压密后，岩石便开始发生微破裂的稳定发展，由（4）式可知，此时孔隙率基本保持不变，相应于蠕变变化特点，即开始进入等速蠕变阶段，蠕变应变率为定值；随着岩石的轴向应变越来越大，岩石物理性质开始劣化，岩石体积开始扩容膨胀，亦由（4）式知，孔隙率开始增大，蠕变应变应变率开始增加，直到破坏。

由此可见，在岩石蠕变破坏过程中，孔隙率的变化与蠕变应变率变化存在紧密联系，孔隙率可以反映出应变率的变化特点。于是本文试图用孔隙率的变化来表征蠕变应变率的变化，假设蠕变应变率是孔隙率的函数，即：

将 f ( n ) 写成幂级数的形式，得：

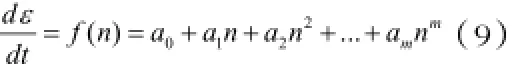
由以上分析可知，当岩石被压密，孔隙率趋近于0，蠕变应变率也趋近于0，故由（9）式有a0= 0 ，同时略去二阶以上的项，得：

3.蠕变模型的建立

3.1稳态蠕变

当蠕变应力较小时，一般只存在稳态蠕变；将（6）式，（7）式代入（10）式可得轴向应变蠕变方程为：

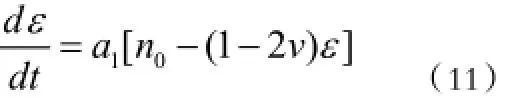
将（11）式积分，并联立边界条件t=0,ε=0，得蠕变方程：

式中：a1, n0, v , ε 分别为常数，初始孔隙率，泊松比，稳态蠕变应变。

由此可见，（12）式与元件模型的稳态蠕变方程类似，符合稳态蠕变曲线的特点。

3.2等速蠕变

当蠕变应力较大时，由前面分析可知，岩石孔隙被逐渐压密后，岩石中的裂隙发生稳定发展，孔隙率维持在一定的值不变，蠕变应变率亦为定值，发生等速蠕变。此时等速蠕变方程为：

将其积分，联立边界条件：

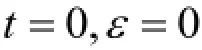
得等速蠕变应变量为：

式中：n1为岩石裂隙稳定发展时的孔隙率值，a1意义与前面相同。3.3加速蠕变

当蠕变应力超过岩石的长期强度时，岩石经过微裂隙的稳定发展后，便开始发生劣化，体积发生膨胀，孔隙率不断增加，蠕变应变率亦逐渐增大，此时加速蠕变方程为：

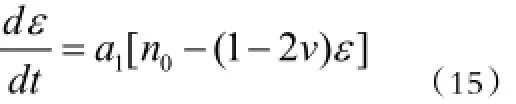
式中：为加速蠕变轴向应变量，侧向应变量；意义与前面相同。但由于该阶段有扩容现象的发生，泊松比不再是常数。

由前面分析可知，当扩容现象发生后，体积膨胀，泊松比随着应变的增大而逐渐增大，假定泊松比服从幂级数规律，即：

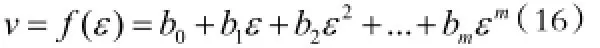
略去二阶以上的项得：

式中：b0, b1, . .. bm为常数。

假设岩石的初始泊松比可取：

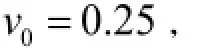
于是从（17）式可知，b0= 0 . 2 5 。

联立（7）式，（17）式，并可知加速蠕变初始孔隙率，n0= n1得：

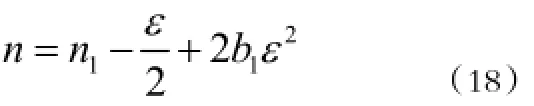
将（18）式代入（15）式，联立边界条件积分可求得加速蠕变方程为：

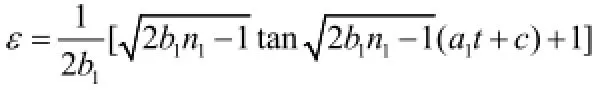
（19）式中：

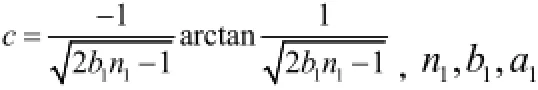
意义同前。

从（19）式可以看出，加速蠕变量是时间的正切函数，符合加速蠕变曲线的特点。

由上面分析可知，对于各种不同的蠕变类型，可以从上述三种蠕变方程中选择合适的方程或其组合来描述岩石的蠕变。

4.结论

（1）岩石在其破坏的过程中，孔隙经历三阶段变化，即孔隙率先变小，孔隙闭合；孔隙率恒定，体积应变保持不变；孔隙率加速增大，发生扩容现象直至岩石破坏。

（2）在岩石蠕变破坏过程中，蠕变应变率的变化表现为先减小、再保持恒定、最后加速增大，对应于蠕变曲线的衰减蠕变、等速蠕变及加速蠕变。

（3）孔隙率变化三阶段对应着蠕变率变化三阶段，两者变化情况存在相似性。基于两者服从线性相关的假设，得出了衰减蠕变、等速蠕变及加速蠕变与孔隙率的关系式，符合岩石蠕变三阶段的变化特征。

[1]周维垣.高等岩石力学[M].北京：水利电力出版社，1990.

[2]蔡美峰.岩石力学与工程[M].北京：科学出版社，2006.

[3]谢和平.岩石混凝土损伤力学[M].徐州：中国矿业大学出版社1990.

[4]徐卫亚，杨圣奇，褚卫江.岩石非线性粘弹塑性流变模型[J].岩石力学与工程学报，2006,25（3）：433-447.