自然数的几何解析
2016-11-17贵州省凯里市第一中等职业学校吴志海
贵州省凯里市第一中等职业学校 吴志海
自然数的几何解析
贵州省凯里市第一中等职业学校吴志海
在数论中,研究素数的分布规律及检验方法依然是热点问题,许多数学工作者曾试图通过不同方式或用各种方法建立起素数模型或鉴别方程,但建模大多采用归纳法,而且是不完全归纳法,以至于对素数模型的普适性检验难于建立模型。由于素数分布不具有统计规律,所以用统计方法研究素数分布函数或素数模型已行不通。因此,从正整数全局出发研究素数或奇素数,抑或全部正整数深层本质的其他表现形式,或许能从普遍规律中发现更普遍的规律。
研究表明,家喻户晓的素数难题哥德巴赫猜想不纯粹是关于素数的问题,而是全部正整数之间相互关系的问题。基于这个认识,本文则从正整数的全局出发,对正整数进行几何化处理,以几何原理来反映正整数的性质,并通过平面坐标来研究正整数中各类数之间的关系。同时基于正整数的几何特征,根据分形几何原理把哥德巴赫猜想“1+1”的问题转换成“2-1”的问题,从而对哥德巴赫猜想的原题进行证明(即证明猜想的正确性,哥德巴赫猜想的方程化方法证明有赖于建立普适的奇素数模型)。
一、正整数分类
目前许多数论文献都把正整数分为奇数与偶数和素数与合数。经分析,正整数中1和2具有其特殊性:1是奇数但不是素数,2既是偶数又是素数。把1和2除外,其他数则可以分为三类:奇素数、偶合数和奇合数。由于1和2有其特殊性和双重性,而其他三类数却具有单一普遍性性质,故在研究素数时,1和2干扰了对素数与偶数之间关系的研究。况且,哥德巴赫猜想也就是关于奇素数与偶合数之间的关系的问题。所以,应该把正整数分为1、2、奇素数、奇合数和偶合数[1]。
二、正整数的几何形及坐标表示
上文已对正整数进行了分类,正整数的分类及其鉴别是基于它们的运算关系。实际上,数的概念源于有形物体的抽象。再回归到自然数的本质,从数与形的相互联系出发,结合平面坐标与图形面积的关系,赋予正整数以几何形的表现形式,这样就可以通过正整数的几何特征形象地反映正整数的性质。
根据正整数单位为1的特点,那么,所有正整数的几何形则由各边长为1、面积为1的立方形堆积而成[2],如图1所示。

图1
一定数量的方格子在平面上的堆积就形成具有某一形状的几何形方格子阵,即正整数的几何化。由于方格子的堆积的面积与数的量具有对应关系,故可以用坐标来表示正整数。由于偶合数可以表示为2MN,奇合数可以表示为(2n+1)(2m+1),其中M,N,m,n为任意正整数,所以,偶合数的坐标则表示为(2M,N)或者(M,2N),奇合数的坐标表示为(2m+1,2n+1),如图2所示。由于方格子在二维方向上无论怎样堆积,奇素数不可能排列成矩形状,故奇素数没有坐标表示。

图2
三、正整数的几何特征
方格子堆积时,方格子阵表现出其独特的几何特征。由正整数的几何形及坐标表示可知,偶合数和奇合数的几何化形状具有矩形的特征,并且偶合数的几何形还具有对称性,如图2所示。因奇素数不能用坐标表示,其几何形则具有非矩形的特征。除1和2的几何形以外,其他正整数的几何形对应的几何特征如下:(1)对称矩形——偶合数;(2)非对称矩形——奇合数;(3)非矩形——奇素数。所以,可以把偶数的几何形称为对称矩形,奇合数的几何形称为非对称矩形,奇素数的几何形则称为非矩形。
四、正整数的加减运算几何描述
基于正整数的几何特征,对某一图形进行拆分和组合,就是正整数加减运算关系的几何化描述,即正整数之间的运算关系与格子图形的拆分、组合相对应,如图3所示。下面就来讨论上文所定义的对称矩形、非对称矩形和非矩形之间的关系。

图3
从分形理论可知[3],如果从某一对称矩形中分解出一个非矩形,余下的部分可能是非矩形,或者是非对称矩形。那么,可以得到这样的推论:对称矩形是可以分解出多个不同的非矩形或非对称矩形。
五、奇合数与奇素数之间的关系
由上述可知,对称矩形可以分解为不同的非对称矩形或非矩形。那对称矩形能分解出几种不同的非对称矩形或非矩形呢?即对于任一偶合数,其所包含的奇素数个数或奇合数个数有多少。下面就来讨论偶合数中奇合数与奇素数的关系:
当偶合数2MN≥6时,由坐标表示可知,有N≥3,M≥1或者M≥3,N≥1。对于偶合数2MN,其包含大于1的奇数个数为:j=MN-1[4]。在不考虑奇合数有重复的情况下【根据坐标的对应关系,奇合数可表示为(2m+1,2n+1)或者(2n+1,2m+1),虽然坐标表示不同,但却是相同的奇合数,所以就有重复的可能】,偶合数(2M,N)所包含的奇合数个数为:
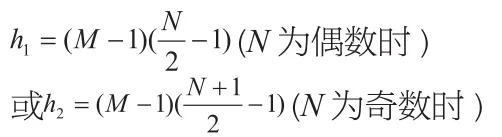
其中h1、h2的表达式是包含重复的奇合数,在不考虑奇合数重复时,则偶合数(2M,N)包含素数的个数为:

分别比较s1与h1,s2与h2。假设:N为偶数时,s1>h1;N为奇数时,s1>h1,即

式(1)等价于:MN+2M+N>MN-2M-N+6……(3)
式(2)等价于:MN+M+N>MN-M-N+4………(4)
在2MN≥6的条件下,不等式(3)(4)成立,故假设成立,即s1>h1,s1>h1。

综合以上证明,可得出这样的结论:任一大于等于6的偶数包含的奇素数大于奇合数,即s>h。如果在考虑奇合数的重复的情况下,假设重复数为H,那么偶合数所包含的奇合数的个数为:=h-H,偶合数所包含奇素数的个数则为:。由于s>h,所以。这也就证明了任意大于等于6的偶合数所包含的奇素数多于奇合数。
由前文可知,从一个对称矩形里分解出一个非矩形后,余下部分有可能是非矩形或者是非对称矩形。由于已证,并在2MN≥6的条件下,-1>同样成立,所以,对于方格子数大于等于6的对称矩形任意分解出一个非矩形后,余下部分必有非矩形,即对称矩形必能分解出两个非矩形。反之,对称矩形必能由两个非矩形组合而成。
因此,本文的“2-1”的分形原理间接地证明了哥德巴赫猜想“1+1”的原命题。
[1]宋树魁,宋昊.破解素数奥秘:哥德巴赫猜想原题的证明[M].西安:西北工业大学出版社,2008.
[2]Pappas,T.李中译.数学还是这么有趣[M].北京:电子工业出版社,2008.
[3]沙震,阮火军.分形与拟合[M].杭州:浙江大学出版社,2005(3).
[4]G.H.Hardy,E.M.Wright.张明尧,张凡 译.数论导引[M]..北京:人民邮电出版社,2008.
