数学思想——数学解题的灵魂——例说数学思想在数列解题中的运用

江苏省徐州市铜山区大许中学　刘　影

数学思想——数学解题的灵魂——例说数学思想在数列解题中的运用

江苏省徐州市铜山区大许中学刘影

数列是中学数学的重要组成部分，数列中的相当一大部分问题都可以体现数学的重要思想方法去处理。比如，数列中的基本量的确定可以依赖方程，把数列看成特殊的函数，可以借助于函数的思想方法研究，探究性的问题可借助于特殊化和赋值的方法。因此，以重要的思想方法来指导数列解题显得尤为重要，本文就数学思想方法在数列中的应用，举例说明。

数列；数学思想

一、方程的思想

例1公差不为零的等差数列｛an｝的前n项和为Sn。若a4是a3与a7的等比中项，S8=32，则S10=________。

解析：由a4=a3a7得

（a1+3d）2=（a1+2d）（a1+6d）得

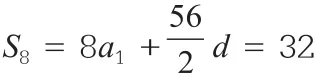
2a1+7d=8，则d=2，a1=-3，

答案：60。

【评注：函数、方程、不等式是一个整体，知道其中任何一个，都可以往其他两个转化，数列中的方程思想主要是是利用数列中的基本量来确定数列，进而可以明确数列的通项和前n项和的表达式来处理问题。】

二、特殊化思想

例2等差数列｛an｝中，公差d＞0，前n项和为Sn，a2·a3=45，a1+a5=18。

（1）求数列｛an｝的通项公式；

因为bn+1-bn=2（n+1）-2n=2（n∈N＊），

所以数列｛bn｝是公差为2的等差数列。

【评注：存在型探索性问题，是指判断在某些确定条件下的某一数学对象（数值、图形、函数等）不确定的问题。这类问题常常出现在“是否存在”“是否有”等形式的疑问句中，以示结论有待于确定。解答此类问题的思路是：通常假设题中的数学对象存在（或结论成立）进行特殊化，然后在这个前提下进行逻辑推理，找到命题成立的必要条件，进而进行充分性的论证。】

三、局部与整体思想

例3设数列｛an｝是由正数组成的等比数列，Sn是其前n项和，

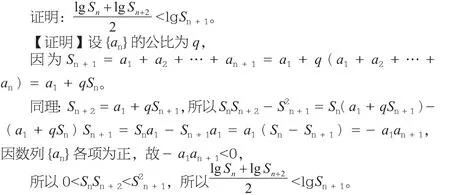
【评注：有些问题如果不从问题结构特点加以认真分析、揣摩，而直接从常规方法入手，往往会走入解题的泥潭，既费时又费力，而如果从整体思维切入，可取得意想不到的效果。若对Sn，Sn+1，Sn+2做整体变换，则可省去分类讨论及复杂计算，轻松获证。结构的巧妙转变，新颖别致，取得了意想不到的效果，给解题带来了新意，也成为解题新的思维亮点。】

四、转化与划归思想

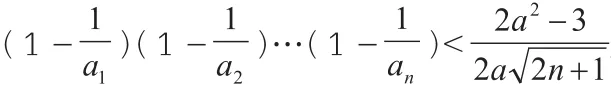
【评注：所谓转化思想，就是在研究和解决有关数学问题时，采用某种手段将问题通过变换使之转化，进而达到解决的一种方法。一般总是将复杂的问题通过变换转化为简单的问题，将难解的问题通过变换转化为容易变换的问题，将未解决的问题变换转化为已解决的问题。在处理多元的数学问题时，我们可以选取其中的常量（或参数），将其看作“主元”，而把其他的变元看作常量，从而达到减少变元简化运算的策略。】

数学思想方法与数学知识一样，是人类在长期研究数学的过程中总结出的宝贵经验和智慧结晶，是数学知识所不能替代的。只有知识与思想方法并重，知识与思想方法互相促进，才能更深刻地理解数学，从整体上认识数学，灵活地运用数学以至创造数学。恰当地运用这些思想方法，可以起到事半功倍的效果。