一种滤除电力线噪声的数字滤波器的设计

张秀芳，徐东明

(西安邮电大学 通信与信息工程学院，西安 710061)



一种滤除电力线噪声的数字滤波器的设计

张秀芳，徐东明

(西安邮电大学 通信与信息工程学院，西安 710061)

数字滤波是信号处理中滤除噪声干扰的常用方法之一;针对信号通过电力线信道传输后出现严重失真这一问题，基于MATLAB平台的工具箱函数，采用窗函数法(选用哈明窗)设计出一个50阶的数字FIR带通滤波器，借助MATLAB仿真对滤波前后的波形作对比和频谱分析，并通过硬件实现电路测试，结果表明所设计的FIR带通滤波器能够有效地滤除带外信号以及电力线噪声，还原出[0.16,0.24]频带内的有用信号，保证了电力线载波通信的可靠进行。

数字滤波；噪声；MATLAB；窗函数法；数字FIR带通滤波器

0 引言

随着数字信息时代的来临，数字信号处理技术已经被普遍地应用到了很多领域，其中应用广泛且较为基础的就是数字滤波器，它的核心任务为从混杂噪声干扰的信号中提取有用信息，同时抑制其它信号和干扰[1]。电力线载波通信技术近些年才出现，但因为它具有巨大的市场潜力和广阔的发展前景，所以一经出现即被企业和科研机构争相采用。然而，电力线作为通信传输介质来讲，有噪声污染大、信号衰减强、电路负载多等诸多有碍信息传输的特性[2]，这增加了数字滤波器的设计难度。

按照传统步骤设计数字滤波器时，往往要先进行复杂的公式计算才能求得滤波器系数，修改参数变量后又需再次计算，这样不仅求解过程繁琐，计算量加大，而且不能随时调整滤波特性，极大地影响了它的应用，而利用MATLAB能够快捷可靠的完成常用数字滤波器的设计和研究。本文借助窗函数法设计数字滤波器的例子，充分证实了MATLAB平台设计FIR带通滤波器的优越性。

1 FIR滤波器的原理

数字滤波器按其单位冲击响应函数的时域特性分为：无限冲击响应(Infinite Impulse Response，IIR)滤波器和有限冲击响应(finite lmpulse response，FIR)滤波器。和IIR滤波器相比，FIR采用非递归结构，能够在有限精度运算范围内确保良好的稳定性；更重要的是，FIR滤波器不仅能够符合幅频响应要求，还能保证严格的线性相位。故而，FIR滤波器在诸如音频、图像、数据传输等对保真度要求较高的信号处理中备受推崇[3]。

1.1 FIR滤波器的基本理论

有限冲击响应滤波器单位冲击响应记作h(n)(0≤n≤M-1)，经过Z变换得其系统函数[4]为：

(1)

分析H(z)展开式及其零极点分布情况可得：H(z)是稳定的，又是非递归系统，没有反馈回路。相应的时域关系表达式为：

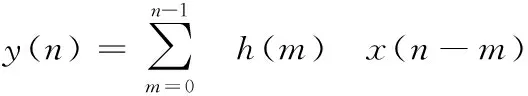
(2)

FIR滤波器基本结构：

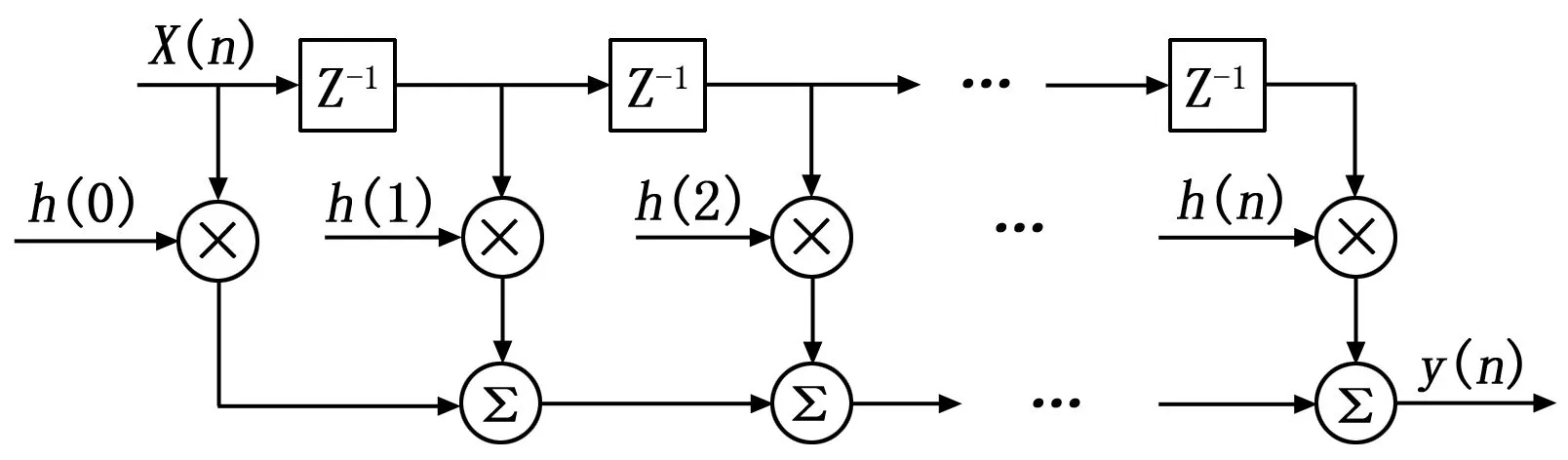
图1 FIR滤波器基本结构

一个完整的滤波器设计过程包括：确定指标、模型逼近、仿真分析。目前，设计FIR滤波器的常见方法有窗函数设计法、频率采样法和切比雪夫最佳逼近法(又称等纹波和最小平方法)，它们都是在理想滤波器频率特性的基础上做某种近似[5]。其中，窗函数法计算简单、物理意义清晰，设计思路比较完善、成熟，因而获得了更多的关注和运用。

1.2 窗函数设计法

窗函数法其主要思想是先选取某一合适的理想频率特性选择滤波器，然后拿一定宽度的窗函数去截断无限长的脉冲响应以获取一个具有线性相位和因果特性的FIR滤波器[6]。因此，选择合适的窗函数和理想滤波器对整个过程至关重要。

窗函数法设计过程[7-8]：

1)根据滤波指标确定窗函数类型，并估算窗口长度M。

2)构建想要逼近的频率响应函数Hd(ejw)。

3)计算hd(n)。上面已给出Hd(ejw)，用傅里叶反变换公式求出hd(n)，hd(n)是无限长非因果序列：

(3)

4)加窗得到结果：h(n)=hd(n)w(n)。采用有限长窗函数w(n)去截取无限冲击响应hd(n)的一段记作h(n)，用来近似表示hd(n)，这样就使原系统变为物理可实现系统。

1.3 窗函数的选择

工程中常用的6种典型窗分别是：矩形窗(Rectangle)、三角窗(Bartlett)、汉宁窗(Hanning)、哈明窗(Hamming)、布莱克曼窗(Blackman)和凯塞窗(Kaiser)。基本参数归纳如表1所示。

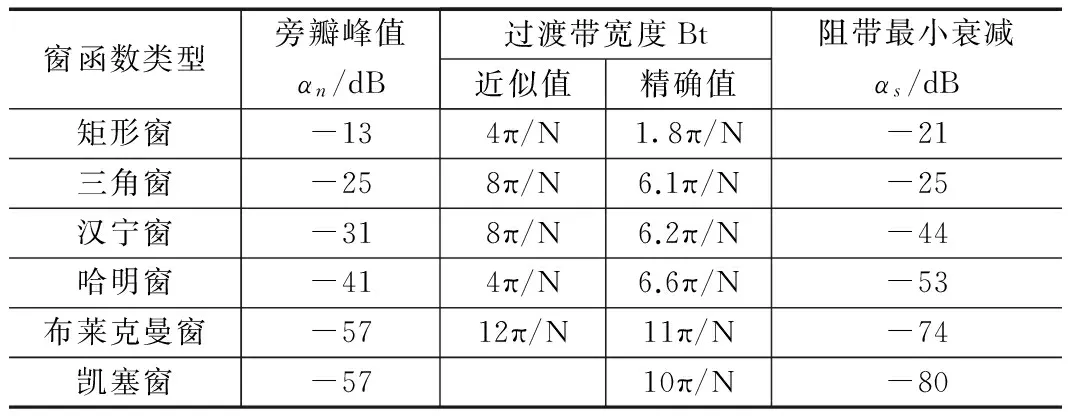
表1 6种典型窗函数的具体参数指标

实际应用中常通过变换窗函数的类型来达到改善滤波器特性的目地。窗函数的选择原则是[9]：1)主瓣宽度要尽量取窄些，以得到较陡的过渡带；2)相对于主瓣幅度，旁瓣要尽可能取小，这样才能使绝大部分能量聚集于主瓣内，以便于降低波动的幅度和次数，增加通带平稳性和阻带衰减，如此，主瓣也不可以取太窄。通常，窗函数的性能指标不可能同时满足上述的两个条件，所以实际应用中要折中取优：在保证主瓣宽度满足基本需求的同时，放宽对主瓣宽度的要求来尽量减少旁瓣波动。

2 FIR滤波器的MATLAB设计

利用MATLAB能够快捷可靠地完成常规数字滤波器的设计，且其丰富的资源为建立仿真模型、监控仿真过程、分析仿真结果提供了便利，可更进一步地对比实际需求和滤波性能，更改参数，完成对滤波器的优化[10-11]。

2.1 MATLAB设计FIR滤波器的流程

通常借助MATLAB工具箱函数来完成FIR数字滤波器的窗函数法设计，具体流程如图2所示。

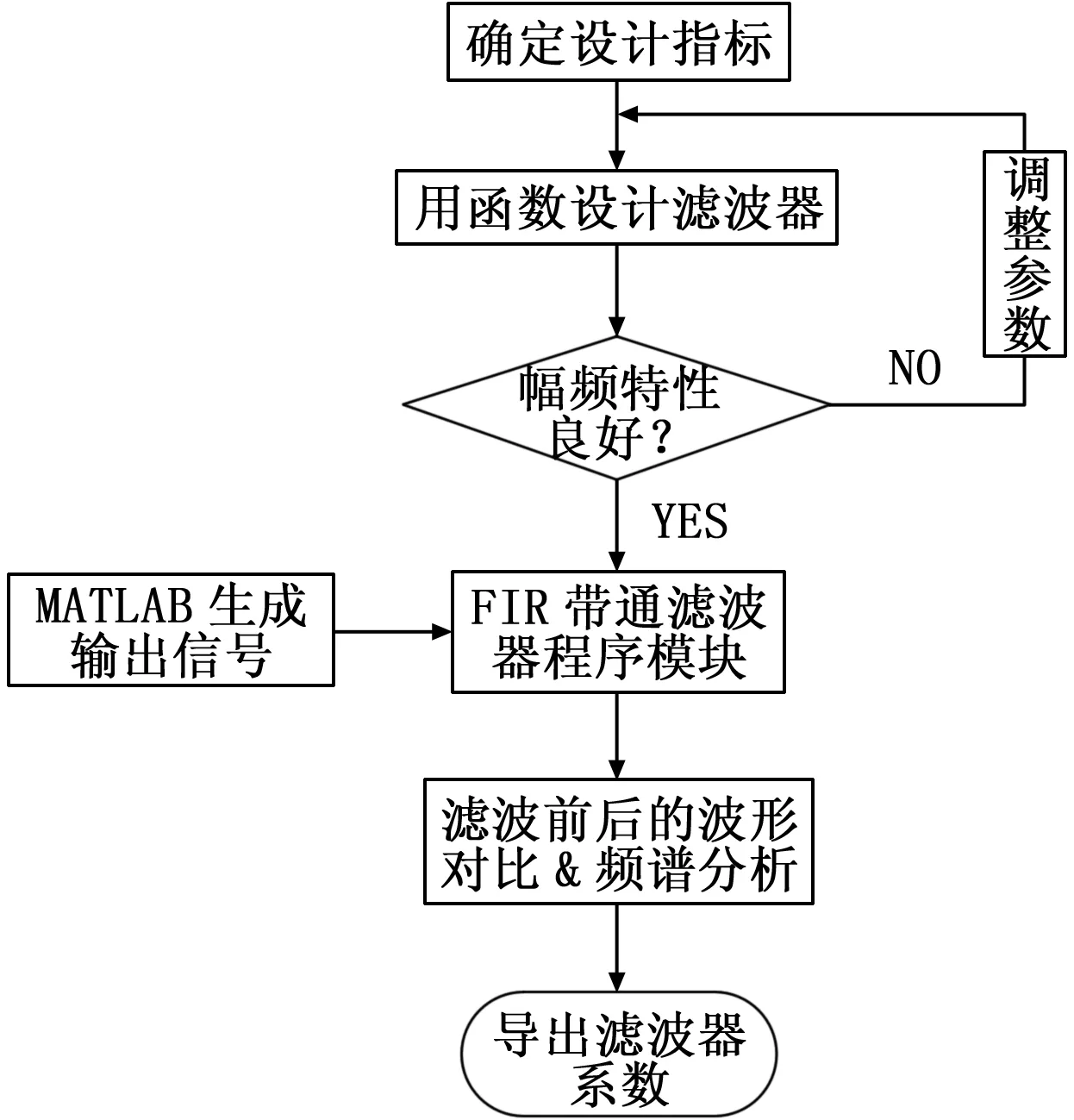
图2 MATLAB设计FIR滤波器的流程图

2.2 FIR带通滤波器的设计

现有一个混合了f1=50 Hz、f2=115 Hz和f3=180 Hz共3种不同频率成分的原信号y0要通过低压电力线信道传输，而且这3种成分的采样频率均取值500 Hz。要求设计一种50阶FIR带通滤波器，能够保留f1=50 Hz这个分量，幅度失真小于1 dB；滤除另外两个分量，衰减不小于45 dB。

首先根据设计要求，确定指标。要求保留f1=50 Hz这个频率成分，所以通带中心频率为f0=50 Hz，按照归一化公式w=2f/Fs，计算出归一化频率w0=0.2；通带边界归一化频率可取0.16和0.24。

确定窗函数类型。根据带通滤波器的指标要求，衰减不小于45 dB，参照表1能够看出，哈明窗、布莱克曼窗和凯塞窗都可提供大于45 dB的最小阻带衰减，而哈明窗的旁瓣峰值比其余两个都小，因此优先选取哈明窗。另外，该信号在电力线信道中传输，所以滤波器除了要滤除另外两个频率成分的信号之外，还要滤除电力线信道自身产生的噪声，最大程度地还原出f1分量。

编程时调用MATLAB里的工具箱函数fir1进行线性相位数字滤波器的标准窗函数法设计和仿真。调用语句“b=fir1(M,Wn,'ftype',window)”可以得到截止频率为Wn的M阶FIR数字滤波器的系数向量b，b可用数学式子表示为：B(z)=b(1)+b(2)z-1+…+b(n+1)z-n。 0≤Wn≤1，Wn=1对应于采样频率的二分之一。

主要指标参数如下：

w1=0.16;

w2=0.24;

Wn=[w1,w2];

N=50; %M=50的带通滤波器

b=fir1(N,Wn); %默认使用Hamming窗

fvtool(b,1); %可视化工具

其中，fvtool是可视化数字滤波器工具，可以看到滤波器的各种特性曲线，y1是包含了电力线信道噪声的信号。图3给出了所设计的50阶FIR带通滤波器的幅频特性和相频特性曲线。分析(a)、(b)曲线可知，带通滤波器在要求的频带范围[0.16,0.24]内，不仅满足幅频响应特性的要求，而且有严格的线性相位特性，整体上满足指标要求。

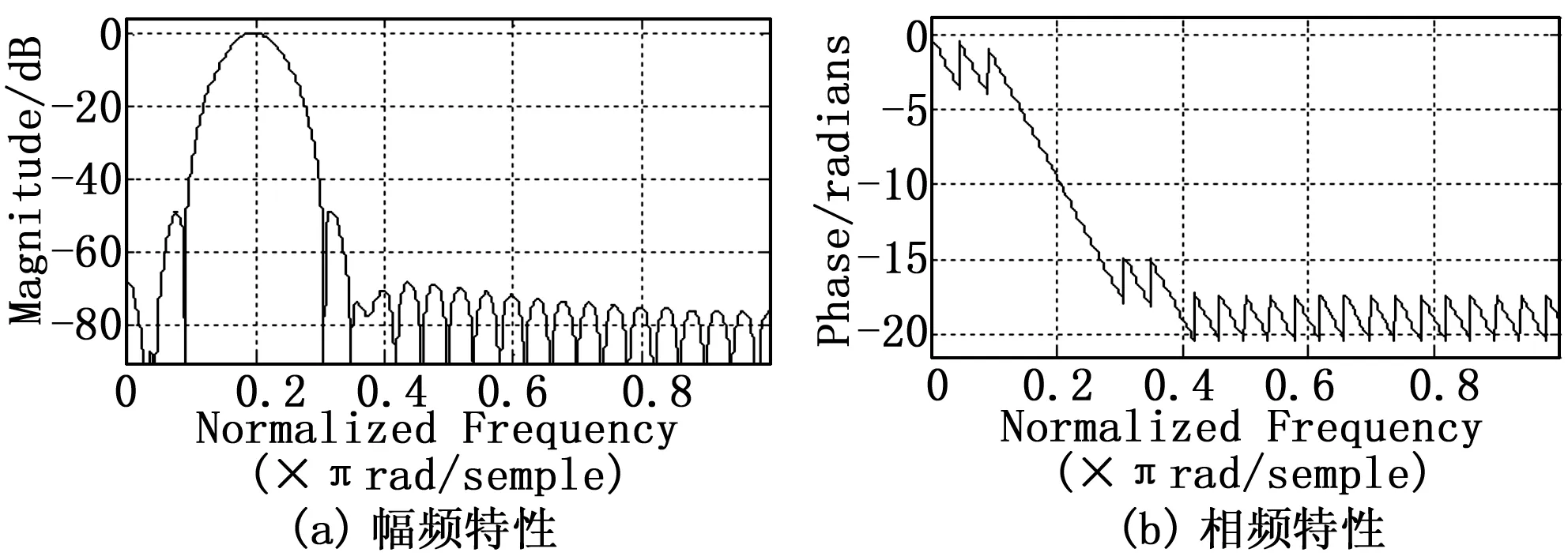
图3 带通滤波器的特性曲线

导出50阶FIR带通滤波器系数(M阶有M+1个系数)，见表2。

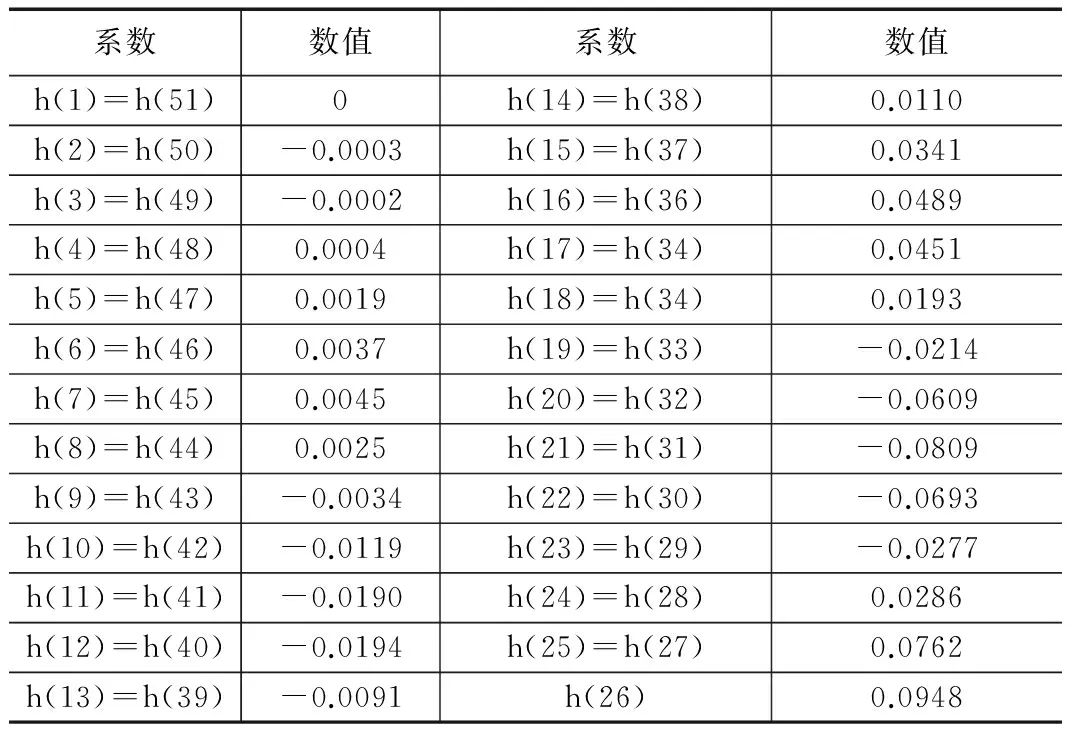
表2 50阶带通滤波器系数表

3 FIR滤波器的MATLAB仿真

3.1 滤波前后的波形比较

y0信号在低压电力线传输过程中受到噪声影响变成y1信号，到达接收端时要先经过滤波处理才能进行其他操作，这里用y2= fftfilt(b,y1)来完成滤波。

图4给出了y1信号以及y1经过带通滤波器滤波后的波形对比图。图(a)是包含了电力线信道噪声的原信号y1，其波形有一定的扭曲和变形，已经无法分辨出有用信号与无用信号；图(a)的y1通过滤波器之后得到图(b)中的y2，与y1曲线相比，滤波后得到的y2波形清晰，信号单一稳定。

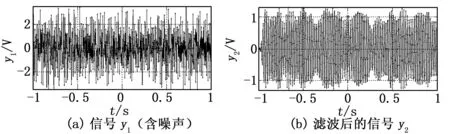
图4 滤波前后的信号对比

y2是用fftfilt函数滤波得到的波形，从(b)图可以看出，在y2的[-1,-0.95]区间，波形出现了严重失真，这是因为fftfilt算法是通过如下差分方程“y(n)=b(1)*x(n)+ b(2)*x(n-1) + ... +b(nb+1)*x(n-nb)”进行滤波处理的。这一段失真是一个瞬态过程，因为输入信号突然从无到有，这是一个突变，滤波器使用递推算法将这个突变从瞬态的变化逐步转到稳态，表现在波形上就是区间[-1,-0.95]的过渡稳定期。

综上所述，设计的FIR带通滤波器有效地滤除了其余频率成分的信号和电力线信道的噪声，还原出50 Hz频率成分的信号，达到了滤波器设计的预期目标。

3.2 频谱分析

为了更直观地对滤波前后的信号进行对比，用FFT(快速傅里叶变换)算法对信号进行谱分析，得到信号的频谱如图5所示。

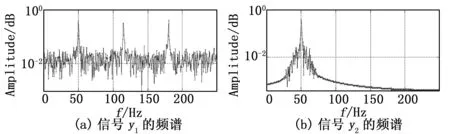
图5 滤波前后信号的频谱

图5(a)是包含电力线噪声的原信号y1的频谱，它的有用信号和干扰信号互不重叠，可以清楚分辨出3个不同的频率成分；(b)是滤波之后的信号y2的频谱，从本图可以更清楚地看到混合信号中的115 Hz与180 Hz频率成分基本被有效滤除，而50 Hz频率成分被完整保留的这一结果。

4 结论

本文针对电力线通信过程中信号衰减强、噪声大的缺陷[12]，借助MATLAB工具，利用窗函数法设计出了一种能有效滤除电力线噪声的FIR带通滤波器，并通过仿真分析滤波前后信号的波形和频谱变化，结果表明，该带通滤波器能有效滤除带外信号和电力线信道中的噪声，完全满足实际需求。另外，由于MATLAB具备强大的接口功能，前端设计工作完成后，可以快捷有效地将仿真结果移植到DSP、CPLD或FPGA等器件中，为下一步的开发工作做准备。

[1] 王赟松. FIR数字滤波器设计[D]. 西安: 西安电子科技大学, 2012.

[2] 杨 晔. 一种适应中国电网的通信电路[J]. 电子元器件应用, 2002(11): 13-16.

[3] 竺小松, 张 颂. 数字FIR滤波器的设计与实现[J]. 世界电子元器件, 2007(10): 89-91.

[4] 潘 登. 基于DSP的数据采集及处理系统设计与实现[D]. 西安: 西安电子科技大学, 2013.

[5] 梁 辰. 基于MATLAB的FIR数字滤波器的设计[J]. 机械设计与制造, 2010, 12: 87-89.

[6] 飞思科技产品研发中心. MATLAB7辅助信号处理技术与应用[M]. 北京: 电子工业出版社, 2005.

[7] 杨大柱. MATLAB环境下FIR滤波器的设计与仿真[J]. 电子技术应用. 2006, (9): 101-103.

[8] 高西全, 丁玉美. 数字信号处理(第三版)[M]. 西安: 西安电子科技大学出版社, 2008.

[9] 张德丰. 详解MATLAB数字信号处理(MATLAB仿真与应用系列)[M]. 北京: 电子工业出版社, 2010.

[10] 刘 波. MATLAB信号处理(MATLAB使用指南系列)[M]. 北京: 电子工业出版社, 2006.

[11] 张绍宸, 常宇辉, 白凤山. 基于FDATool的数字滤波器设计与分析[J]. 农机使用与维修, 2013, 07: 98-99.

[12] 李 伟, 江 楠. OFDM技术在电力线通信中的应用[J]. 电子测试, 2013, 09: 10-11.

Design of Digital Filter for Filtering out Power Line Noise

Zhang Xiufang，Xu Dongming

(School of Communication and Information Engineering, Xi′an University of Posts and Telecommunications, Xi′an 701061, China)

Digital filter technique is one of the methods that commonly used to filter out noise in the signal processing. The signal often appears serious distortion issue after power line channel transmission. For this problem, based on MATLAB toolbox functions, window function method (Hamming window) is adopted to design a 50-order FIR band-pass filter, and compare the waveform before and after filtering, and spectrum analysis. Through the hardware realizating circuit testing, the results illustrate that the designed FIR band-pass filter can effectively filter out out-of-band signals and power line noise, restoring the useful signal, which provides a strong guarantee for reliable power line carrier communication .

digital filtering; noise; MATLAB; window function; digital FIR band-pass filter

2015-12-16；

2016-01-15。

陕西省重大科技创新项目(2015ZKC01-02)。

张秀芳(1989-)，女，河南济源人，硕士研究生，主要从事电子与通信工程方向的研究。

徐东明(1963-)，男，湖北武汉人，教授，硕士研究生导师，主要从事专用集成电路设计方向的研究。

1671-4598(2016)06-0199-03

10.16526/j.cnki.11-4762/tp.2016.06.055

TN713

A