冲击噪声下基于相关熵的二维ESPRIT算法
2016-11-17赵季红李雷雷王伟华马兆恬
赵季红,李雷雷,曲 桦,王伟华,马兆恬
(1.西安邮电大学 通信与信息工程学院,西安 710061;2.西安交通大学 电子信息学院,西安 710049)
冲击噪声下基于相关熵的二维ESPRIT算法
赵季红1,2,李雷雷1,曲 桦2,王伟华2,马兆恬1
(1.西安邮电大学 通信与信息工程学院,西安 710061;2.西安交通大学 电子信息学院,西安 710049)
针对基于相关函数的波达方向(direction of arrival, DOA)估计方法在冲击噪声环境下性能下降明显甚至失效的问题,提出基于相关熵 (Correntropy)的二维ESPRIT算法;该方法利用相关熵在冲击噪声环境下具有鲁棒性的优点,将受干扰信号的自相关函数替换为相关熵函数,并结合二维ESPRIT算法实现在冲击噪声环境下进行二维DOA估计;仿真表明,与基于分数低阶统计(Fractional Lower Order Statistics, FLOS)算法相比,该算法呈现明显优势,特别在高的冲击噪声条件下(1<α<1.5)能对信源方向进行更加有效的估计,且均方误差值仍保持很低。
相关熵;波达方向估计;冲击噪声;分数低阶统计;二维ESPRIT算法
0 引言
传统波达方向估计方法[1-2]大多针对高斯白噪声背景提出,而实际中,由于山脉、森林和海浪等影响,信号呈现突然的破裂或峰值,使得实际噪声环境具有很强冲击性。此时传统基于高斯噪声背景的算法性能大幅下降甚至失效[3-4],因此针对冲击噪声背景下的DOA估计是DOA估计中的重要研究方向。
基于相关函数的波达方向估计在传统方法中已经得到了广泛的应用,但其只反映了信号间的二阶矩统计特性,在冲击噪声背景下,其处理能力会显著下降。为了抑制冲击信号,部分基于分数低阶统计的方法[5-8]被应用于DOA估计。基于分数低阶矩 (FLOM) 的算法[6]放宽了信号和噪声中α-stable的约束条件。文献[7]分析并给出了FLOM-MUSIC和FLOM-ESPRIT算法的仿真。但以上几种算法仅对两个变量中的一个起到抑制冲击值的作用。为克服该缺点文献[8]提出了基于子空间算法的相位分数低阶矩(PFLOM)。
尽管上述基于分数低阶统计量的算法都具有鲁棒性,但这些方法大多只考虑了弱冲击噪声情况,故在低信噪比情况下,性能大幅下降。为了能够更精细地划分空间并且提高低信噪比情况下的系统性能,本文中将基于相关熵的相关性度量准则[9]与二维ESPRIT算法[10-12]相结合,提出了基于相关熵的二维ESPRIT算法。
1 阵列结构和信号模型
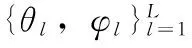
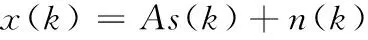
(1)
其中:A为信号导引矢量,向量s(k)=(s1(k),s2(k),…,sL(k))T为期望信号,n(k)=(n1(k),n2(k),…,nM(k))为加性噪声,第l个信号导引矢量为:
其中:λ为信号波长,τml为第l个信号到达第m个阵元时相较参考点的时延:τml=xmcosφlsinθl+ymsinφlsinθl+zmcosθl。
冲击噪声环境使用对称的α-stable分布[13](SαS)建模,其特征函数定义如下:
(2)
其中:η(-∞<η<∞)为位置参数,相当于高斯分布的均值,γ(γ>0)为分散系数,对应高斯分布的方差,α(0<α≤2)为特征指数,表示α-stable分布的拖尾特征,当α=2时为高斯分布。因为SαS分布噪声的方差并不存在,所以本文使用信号平均功率和噪声分散系数γ的比值代替传统的信噪比定义,即广义信噪比(GSNR, Generalized Signal-to-Noise Ratio)来代替一般的信噪比,其表达式为:
(3)
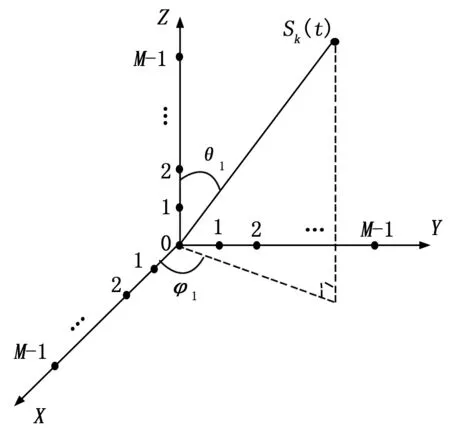
图1 二维到达角的空间关系图
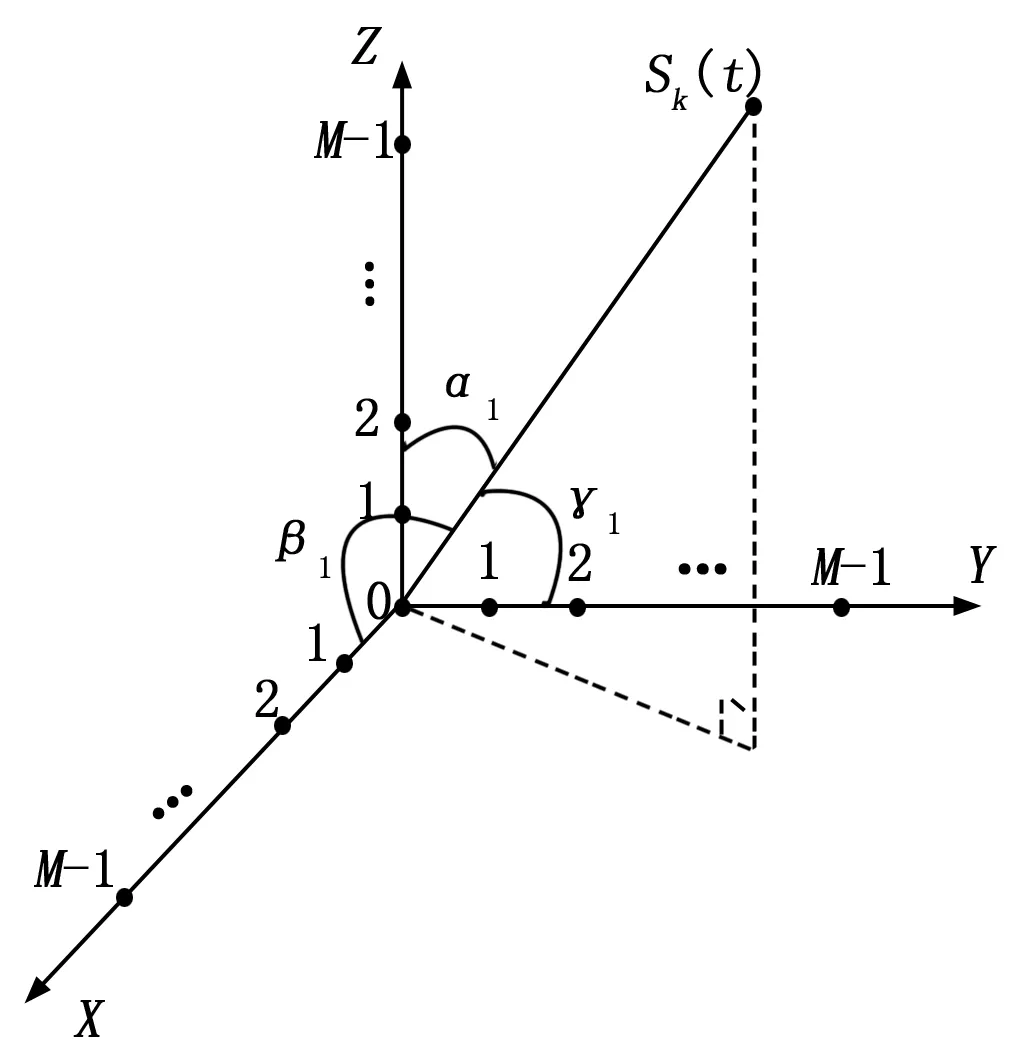

图2 接收信号到达参考点时与各坐标轴的夹角
(4)
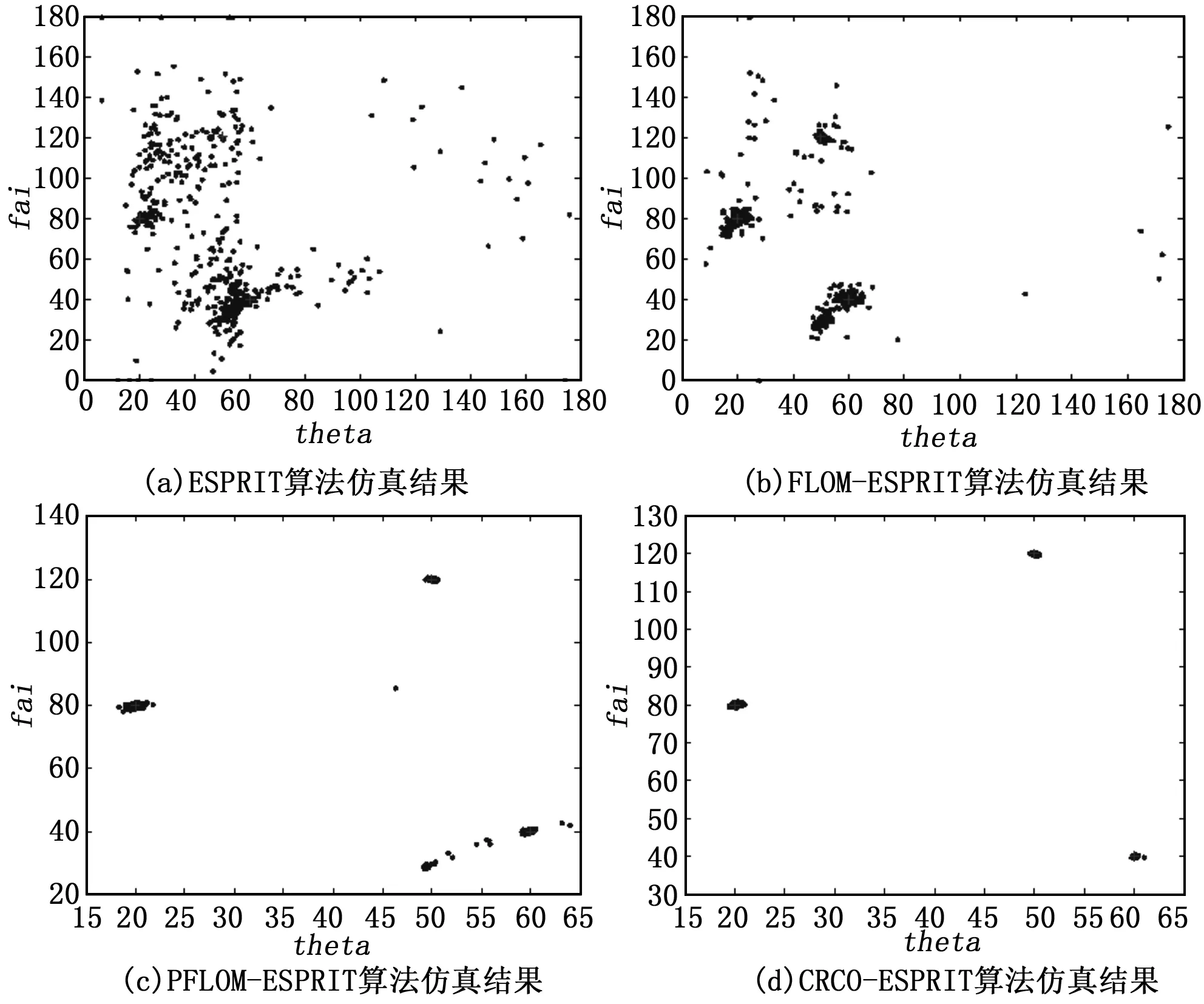
由图1可知,3个与一维阵列相同的均匀线阵分别分布在3个坐标轴上构成了二维方向估计的天线阵列。本文对3个坐标轴进行拆分,将每个坐标轴作为一组线阵,每个线阵配置M个阵元。L(L (5) 其中:s(t)为期望信号向量,n(t)为信号在传输过程中的加性噪声,Ax(α)、Ay(β)、Az(γ)分别为3个坐标轴上线性阵列的阵列矢量: (6) 其中: (7) 本文采用了基于相关熵的相关性 (CRCO, Correntropy based Correlation) 度量准则,并将其与二维ESPRIT算法相结合,提出了基于相关熵的二维ESPRIT算法 (CRCO-ESPRIT),该方法在高冲击噪声环境下较FLOS-ESPRIT和PFLOS-ESPRIT有明显的性能提升。 2.1 相关熵函数 若随机变量X和Y为服从独立同分布的对称的α-stable分布,则基于相关熵的两个随机变量X和Y的相关性定义为: (8) 式中,σ为核宽度,阵列输出协方差矩阵对应传统ESPRIT算法的自相关函数。在确定出合适的核宽度后,当接收数据中出现较大的冲击噪声时,指数项变小,使得计算结果中该处协方差元素的整体值减小,降低了冲击噪声对于计算结果的影响。然而,公式 (8) 仅定义了基于相关熵的互相关,当X=Y时,基于相关熵的自相关函数不存在,取而代之的仍是传统的自相关函数。为了解决这个问题,可以将公式 (8) 推广为: (9) 式中,μ为正常数且μ≠1,1<α≤2,E[·]表示数学期望。 相关熵可以在样本空间诱导一个新的度量标准CIM (Correntropy Induced Metric),表示为: (10) 2.2 算法介绍 本文假设系统中各期望信号之间不相关;信号与噪声、噪声与噪声之间均相互独立且信号数不大于阵列天线数。基于以上系统假设,依据二维ESPRIT算法的阵列模型,将z轴上M个阵元天线分为两组,每组个数为m,则对于每组阵元,L个接收信号分别为: (11) (12) 依据公式(9)计算z轴接收数据的相关熵,其矩阵形式为: (13) (14) 其中:μ为正常数且μ≠1,1<α≤2,zi(t)和zj(t)是z轴上接收到的信号向量z(t)的第i个和第j个元素。 (15) 其中,Range{ ·} 表示矩阵中的向量张成的空间。因此,一定存在一个满秩矩阵Tz,使得: (16) (17) 必然惟一存在一个秩为L的矩阵Fz∈C2L×L满足: (18) (19) 2.3 角度匹配 (20) 在实际应用中,由于接收信号中必然存在噪声,因此在角度估计的过程中会存在一定的误差,使得估计的结果并不严格满足上式的关系,而是出现一定的偏差,此时不能再继续使用上式来对角度进行配对,需要对上式进行改进,通过求解公式(21)来进行角度的配对: (21) 其中:min{·}表示求取最小值操作。在对3L个角度值进行配对组合之后,得到L组来波信号与3个坐标轴的夹角,继而使用公式(4)对角度进行转换,得到来波信号三维角度的真正估计值,即方位角和俯仰角。 在仿真中,假定3个相互独立的16进制正交振幅调制信号(16-QAM),接收到的用户信号三维角度中,方位角φl为[80° 120° 40°],俯仰角θl为[20° 50° 60°],天线阵列为如图1所示的双L型阵列,每个坐标轴上由8个天线阵子组成的间距为半波长的等间距线性阵列,其中原点处阵元为3个坐标轴共用。快拍数N为600,每个仿真实验均进行100次独立的蒙特卡罗试验。仿真实验所用到的信号和噪声分别为远场窄带信号源和SαS分布的噪声,算法的性能由方向估计的正确率以及均方误差来评估。与之作对比的有传统的二维ESPRIT算法[11]、FLOM-ESPRIT算法[7]以及PFLOM-ESPRIT算法[8]。 图3 DOA估计仿真结果图 首先,图3(a)到图3(d)在冲击噪声特征指数α的取值均为1.1情况下比较了4种二维DOA估计算法。由图中可以看出,基于相关熵的DOA估计算法性能明显优于其它3种算法,在较高的冲击噪声下,传统ESPRIT与FLOM-ESPRIT算法已经无法正确判断出信号源的方向。由图3(d)中可以看出,在10 dB的信噪比条件下,方位角和俯仰角的测向精度均保持在3°以内。故可以得出结论:相比基于FLOS的算法,基于相关熵的二维ESPRIT算法估计的正确率更高,抑制冲击噪声的效果更为明显。 其次,图4、图5分别对不同GSNR值条件下4种算法的正确率及均方误差进行了比较。令GSNR的值从2 dB变化到10 dB,两图中冲击噪声特征指数α的取值均为1.6。可以看出,在较低的广义信噪比条件下,传统二维ESPRIT与FLOM-ESPRIT算法已经无法正确判断出信号源的方向,即使与基于PFLOM的ESPRIT算法相比,基于相关熵的二维ESPRIT算法仍具有较强的优势,估计出的信号方向正确率更高,均方误差更小。 图4 不同GSNR条件下4种算法正确率对比图 图5 不同GSNR条件下4种算法MSE对比图 最后,如图6、图7所示,分别对比了在不同的α值条件下4种算法的性能。比较了不同特征指数(即α值)对于各算法性能的影响。在该仿真中测试了α值从1~1.5变化过程中4种算法的正确率及均方误差,两图中广义信噪比GSNR的取值均为6。由两图可以看出,在较高的冲击噪声环境中,相比基于FLOS的算法,基于相关熵的二维ESPRIT算法估计出的信号方向中正确率始终接近于1,误差始终接近于0,仿真效果较好。 图6 不同α值条件下4种算法正确率对比图 图7 不同α值条件下4种算法MSE对比图 本文提出了一种基于相关熵的二维ESPRIT算法,给出了基于相关熵的协方差矩阵公式,并将其与二维ESPRIT算法相结合来获得二维DOA估计值。该算法利用相关熵中协方差函数的内在鲁棒性,将基于传统协方差的二维ESPRIT扩展为基于相关熵的二维ESPRIT算法。仿真结果显示,提出的算法比基于FLOS的二维ESPRIT算法性能更好,尤其在高的冲击噪声或低的广义信噪比环境中。 [1]He J, Swamy M N S, Ahmad M O. Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources [J]. IEEE Transactions on Signal Processing, 2012, 60(4) : 2066-2070. [2]Choi Y H. ESPRIT-based coherent source localization with forward and backward vectors [J]. IEEE Transactions on Signal Processing, 2010, 58 (12) : 6416-6420. [3]Fernandez M, Landa I, Arrinda A, et al. Measurements of Impulsive Noise From Specific Sources in Medium Wave Band[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13:1263-1266. [4]Zhao D Y, Gao H Y, Diao M, et al. Direction finding of maximum likelihood algorithm using artificial bee colony in the impulsive noise [A]. IEEE Conference on Artificial Intelligence and Computational Intelligence[C]. Sanya: [s. n.], 2010: 102-105. [5]Zhao X H, Premkumar A B, Madhukumar A S. Direction of arrival tracking in impulsive noise using particle filtering with fractional lower order moment likelihood [A]. IEEE Conference on Information, Communication and Signal Processing[C]. Singapore: [s. n.], 2011 : 1-5. [6]Akhtar M T. Fractional lower order moment (FLOM)-based adaptive algorithm with data-reusing for Active noise control of impulsive sources[A]. 2013 International Conference on Signal-Image Technology & Internet-Based Systems (SITIS)[C]. IEEE, 2013:31 - 37. [7]韩晓东. 冲击噪声背景下的测向算法研究[D]. 哈尔滨:哈尔滨工程大学, 2012. [8]Hongjun S, Shang X Q, Zheng J B. 2-D Direction of arrival estimation algorithm in impulsive noise[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(6):844-848.[9]Liu W F, Pokharel P P, Principe J C. Correntropy : properties and applications in non-gaussian signal processing [J]. Signal Processing, IEEE Transactions on. 2007, 55(11): 5286-5298. [10]Chen F J, Kwong S, Kok C W. ESPRIT-Like two-dimensional DoA estimation for coherent signals [J]. Aerospace and Electronic Systems, IEEE Transactions on. 2010, 46(3): 1477-1484. [11]杨荣山, 张 宁, 张 玉. 基于L型阵的ESPRIT算法在DoA估计中的应用[J]. 无线电通信技术. 2013, 39(4): 85-88. [12]Xu X, Ye Z. Two-dimensional direction of arrival estimation by exploiting the symmetric configuration of uniform rectangular array [J]. Radar, Sonar and Navigation, IET,2012, 6(5): 307-313. [13]Song A M, Qiu T S. The Equivalency of minimum error entropy criterion and minimum dispersion criterion for symmetric stable signal processing [J]. Signal Processing Letters, 2010, 17(1):32-35. [14]Chen Badong, Principe J C. Maximum correntropy estimation is a smoothed MAP estimation [J]. Signal Processing Letters, IEEE, 2012, 19(8):491 - 494. Correntropy-Based Two-Dimensional ESPRIT Algorithm under Impulsive Noise Zhao Jihong1,2, Li Leilei1, Qu Hua2, Wang Weihua2, Ma Zhaotian1 (1. School of Telecommunication and Information Engineering , Xi′an University of Posts & Telecommunications, Xi′an 710061, China; 2. School of Electronic and Information Engineering, Xi′an Jiaotong University, Xi′an 710049,China) In order to solve the problem that the correlation function-based DOA (Direction of Arrival, DOA)estimation method has an obvious performance degradation or even a total efficiency loss in the impulsive noise environment, a new two-dimensional ESPRIT algorithm based on correntropy was proposed. It takes advantage of correntropy’s robustness in the impulsive noise environment, replaces the signal's autocorrelation function with the correntropy function and combines with two-dimensional ESPRIT algorithm to estimate two-dimensional DOA in the impulsive noise environment. Simulation results show that CRCO-ESPRIT outperforms the existing FLOS algorithm and especially can estimate DOA efficiently in high impulsive noise environments(1<α<1.5), and the mean square error still remain at a low level. correntropy; DOA; impulsive noise;fractional lower order statistics; two-dimensional ESPRIT 2015-12-02; 2015-12-29。 国家自然科学基金项目(61371087);新一代宽带无线移动通信国家重大专项项目(2013ZX0302010-003);国家高技术研究发展计划(“863”计划”);(2014AA01A706)。 赵季红(1963-),女,陕西西安人,博士,教授,主要从事宽带通信网、新一代网络的管理与控制方向的研究。 曲 桦(1961-),男,汉,陕西西安人,博士,教授,主要从事新一代无线宽带无线通信技术方向的研究。 1671-4598(2016)06-0170-04 10.16526/j.cnki.11-4762/tp.2016.06.047 TN911 A2 基于相关熵的二维ESPRIT算法
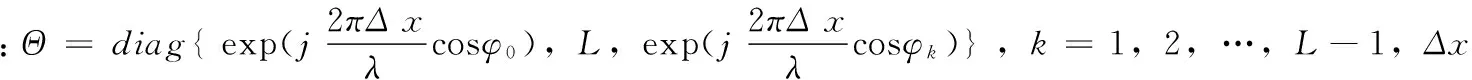
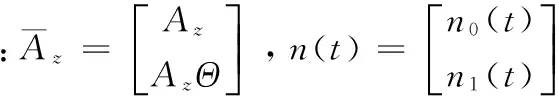
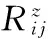
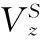
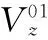
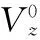
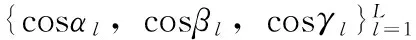
3 仿真实验与分析
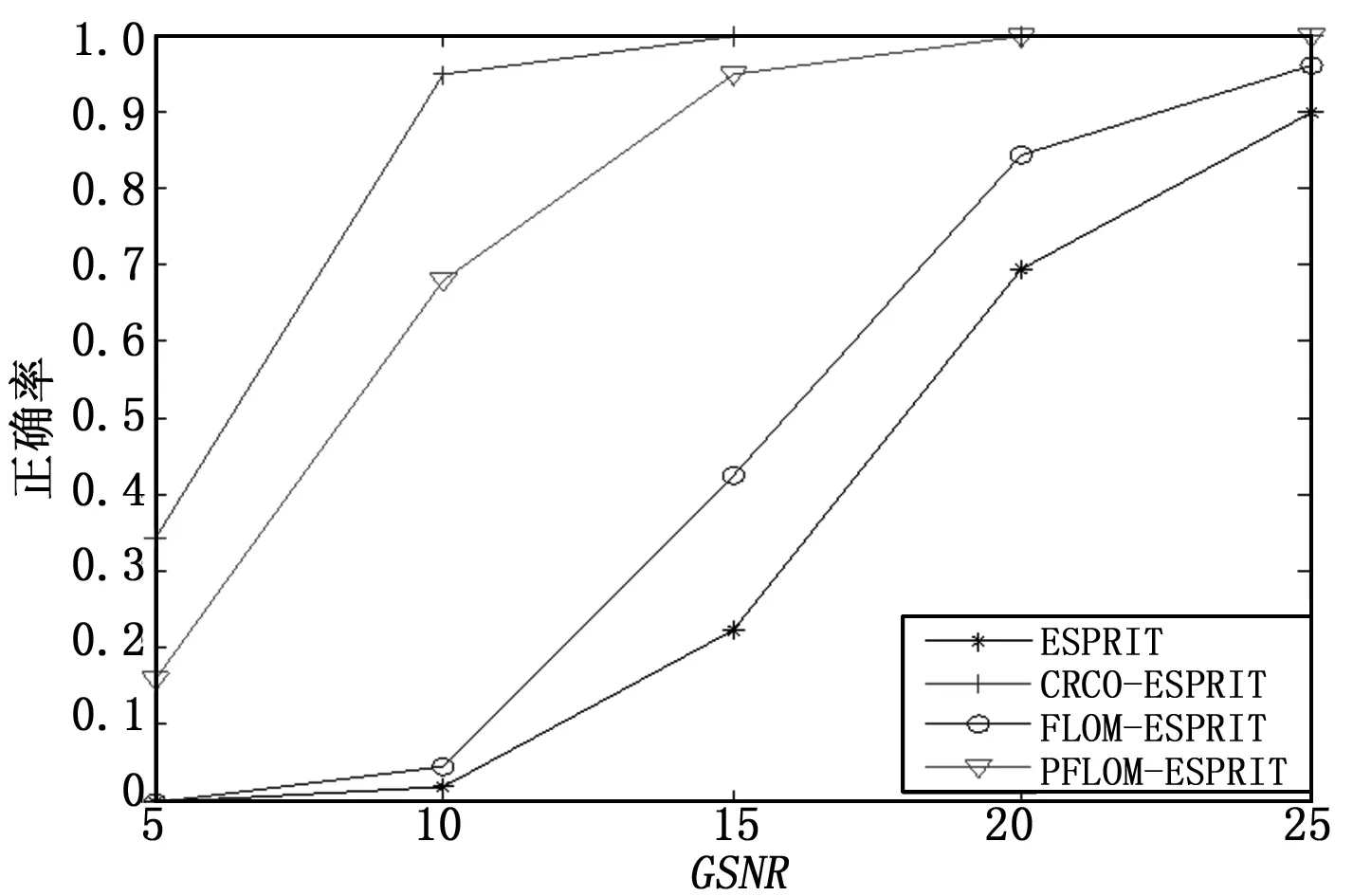
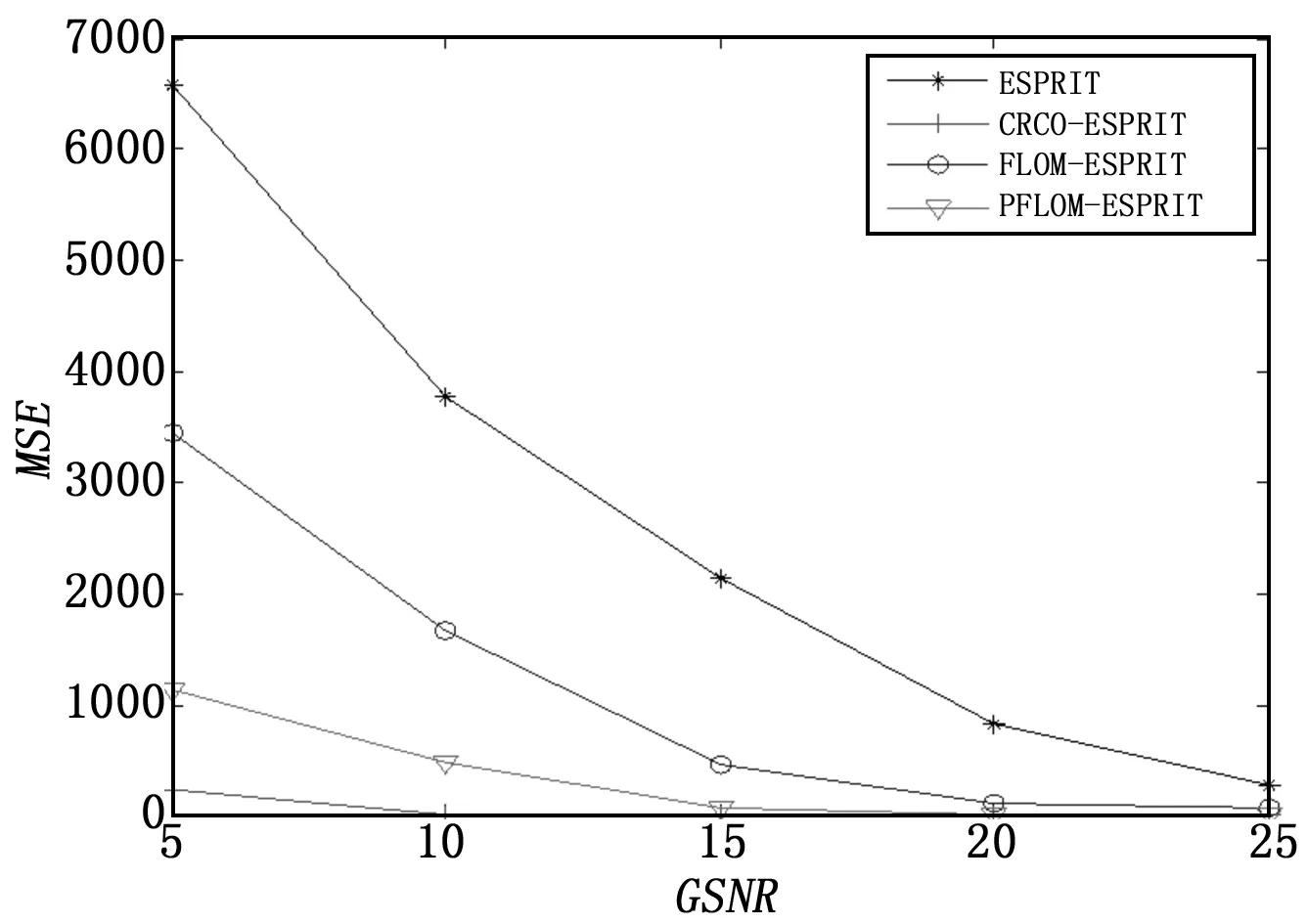
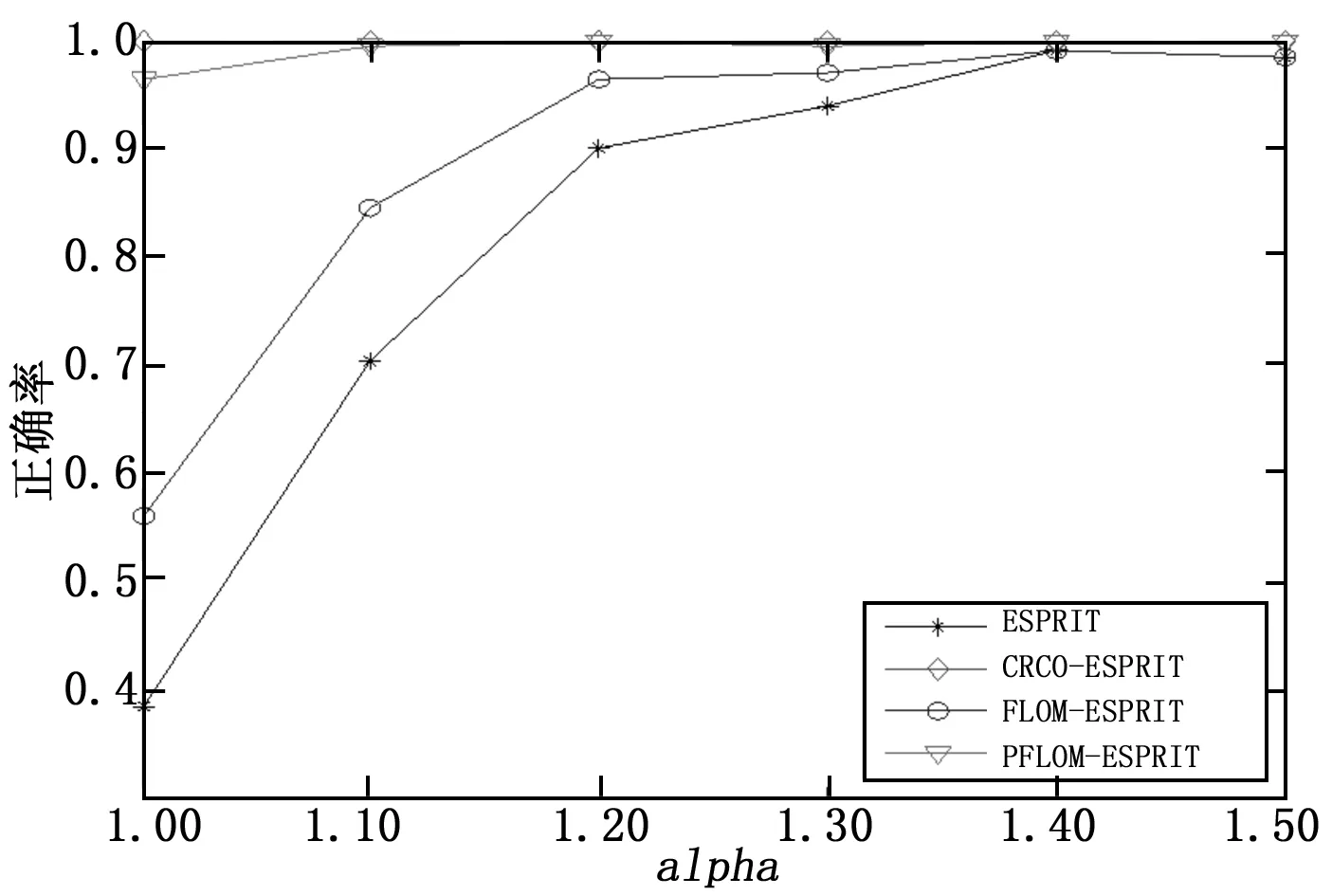
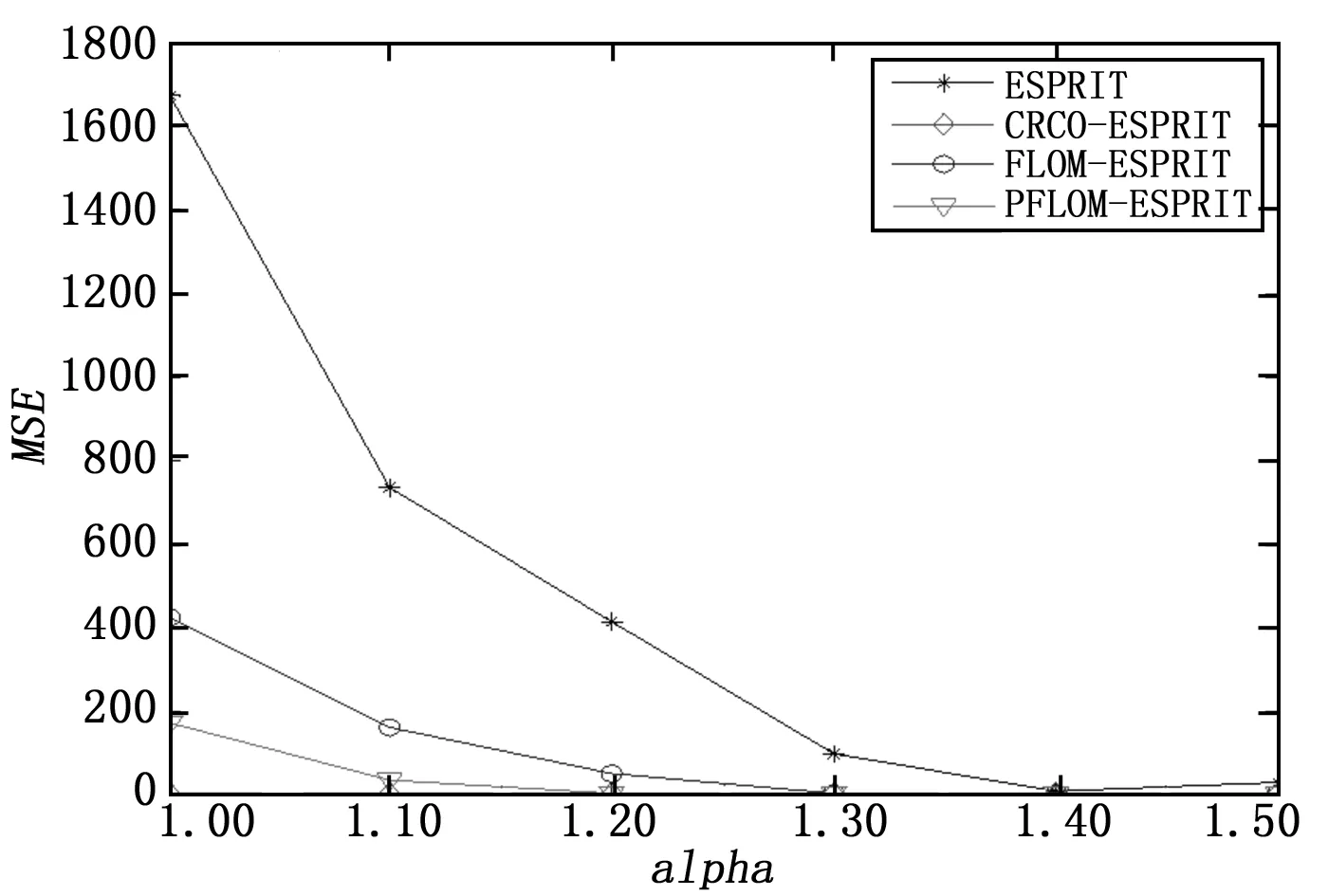
4 结束语
