基于连接矩阵的潜在通路定性分析方法
2016-11-17张庆振
黄 聪,梅 洪,张庆振,程 林
(1.北京航空航天大学 自动化科学与电气工程学院,北京 100191; 2.北京航天自动控制研究所,北京 100854)
基于连接矩阵的潜在通路定性分析方法
黄 聪1,梅 洪2,张庆振1,程 林1
(1.北京航空航天大学 自动化科学与电气工程学院,北京 100191; 2.北京航天自动控制研究所,北京 100854)
对电路图中的电气元件进行定性建模,根据建立的元件模型,按照电流方向将电路图转化为有向图的形式,进而构造出图的连接矩阵,利用其代数余子式计算有向图中从电源正端到地端的所有通路路径,并与该电路图设计的功能支路进行对比确定电路是否存在潜在通路;相比于传统潜在通路分析的邻接矩阵法,该方法不仅能判别电路中是否存在潜在通路,而且能确定潜在通路的所有导通路径信息;在此基础上,提出了改进原始电路图以达到消除潜在通路影响的方法,文中采用某汽车点火电路为例,利用CapitalHarnessSystem(CHS)软件仿真分析,验证该方法的正确性与可行性。
连接矩阵;开关函数;潜在通路分析;CHS
0 引言
潜在通路问题是与元器件失效无关、在特定条件下会导致系统期望功能被非预期地抑制或非期望功能被非预期地激发的这一类问题[1]。潜在通路问题的研究是从上世纪60年代美国红石火箭发射失败时开始,原因是点火后产生意外通路导致发动机关机[1-2]。在航空航天测试中,由于电路系统过于庞大,电气元件种类繁多,在不同时序的开关组合下,可能造成某些功能元件被意外激发,对整个电路系统的安全造成潜在隐患,因此开展电路的潜在通路研究时很有必要的。
传统潜通路分析是通过构建电路有向图,利用邻接矩阵求取电路通路数目,当时序变化导致开关组合发生变化时,邻接矩阵亦随之变化,计算潜在通路过程复杂且只能得出支路数目,无法得出潜在通路回路的具体路径[3]。本文中提出一种基于电路有向图的连接矩阵方法,通过对电器元件定性建模,通过计算连接矩阵代数余子式能直观反映出电路图中所有开关组合下的路径通路[4-6],并与设计的功能支路数进行对比,从而确定是否存在潜在通路并详细指出潜在通路的路径信息[3]。
1 基于图论的电路有向图
对电气元件进行定性建模,把电路图中建模后的功能元件定性转化为图论中的边,按照流过功能元件的电流方向定义边的方向,那么每个功能元件对应的边是有向边,由有向边和顶点集合所构成的图即是有向图。
1.1 电气元件定性建模
电气元件是指能在电路中实现某一特定功能的部件,在实际电路系统为了简化分析过程,先对简单电气元件如电阻、灯、开关等进行定性建模。
图1左边的简单电气元件中,它们都是由端点和所在通路组成,为了简化模型,不论元件是否处于工作状态或者开关是否处于导通状态,我们将除了电源以外的元件都等效成图1右边的模型,其中Ai代表端点,ei代表等效支路[7]。
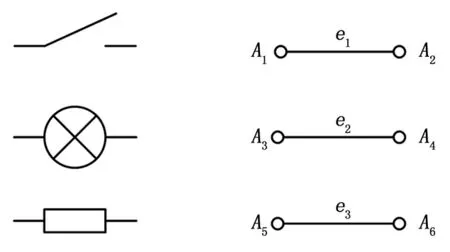
图1 电气元件模型
充分考虑电气元件处于工作或者非工作状态,对应的支路ei取值为0或1。当ei=0时,表示开关打开或者功能元件处于不使能状态,当ei=1时,表示开关关闭或者功能元件处于使能状态。
1.2 电路有向图
按照电源正端到地端的顺序,对每个电气元件的端点进行编号,分别记作A1,A2…AN,从电源正端A1为起始点,选择一个与A1相邻且未被访问的节点Am,再从Am出发选择一个与Am相邻且未被访问的节点An,一直到访问到地端节点,依次循环。根据电流的流向关系,将每条功能元件的边转化为有向边,分别记作e1,e2…en。在图2[1]所示的某汽车点火电路图,将电源正端编号为A1,闪光器1端、2端分别编号为A2、A3,地端编号为A4,停车灯与停车开关相交节点编号为A5,打火开关、刹车开关与收音机相交节点编号为A6,并将危险开关S1、闪光器、刹车灯、停车灯、停车开关、刹车开关、打火开关与收音机分别编号为有向边e1,e2,e3,e4,e5,e6,e7,e8,转化为有向图如图3所示。

图2 某汽车点火电路
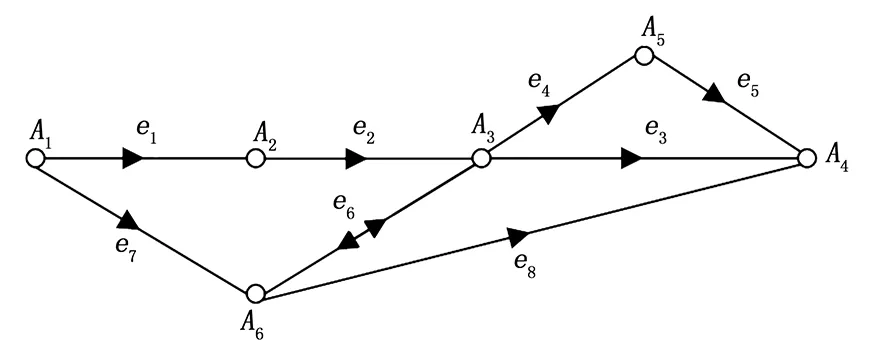
图3 电路有向图
2 电源正端到地端通路计算
2.1 连接矩阵

按照连接矩阵的定义,图2电路的连接矩阵表示为:
(1)
2.2 开关函数
定理1:电路有向图端点Ai和Aj的开关函数Fij等于真值Per Xij(i≠j),其中,Xij表示连接矩阵X除第i行与第j列的子矩阵,Per Xij表示对矩阵Xij取行列式并将所有子项的符号位取绝对值,开关函数是指在开关电路中两个端点之间所有路径的乘积和[8-9]。
证明:在原图G中增加一条边e0,规定该边从Ai出发,指向Aj,得到新图G0。
显然,图G0从Ai到Aj的全部有向路径可以按照是否含有单通边e0分为两大类,一类有向路径中不含单通边e0,记为Dk,另一类有向路径中含有e0,记为e0Pk,可得:
(2)
去掉边e0后G与G0完全相同,因此有:
(3)
由于e0定义为从Ai到Aj的单通边,Pk可以看作由Aj到Ai有向边的积,∑Pk为Aj到Ai的全部有向路径,因此有:
(4)
证毕:

在图2电路中,电源正端对应图3有向图中节点A1,地端对应图3有向图中节点A4,除掉第4行第1列的子矩阵行列式表示为:
e1e2e3-e7e8-e1e2e4e5-e1e2e6e8+e3e6e7-e4e5e6e7
(5)
将|X14|中每条通路前的系数求取绝对值并去掉开关函数中的平方项,得到从电源正端到地端的开关函数为:
F41=e1e2e3+e1ee4e5+e1e2e6e8+e3e6e7+e7e8+e4e5e6e7
(6)
3 潜在通路判定
根据潜在通路的定义,在电路分析中,只需要关注关键元件,分析从电源正端到地端节点的开关函数中含有该元件有向边的实际功能支路数,将此数目与电路设计中该元件正常工作的路径数相比较,即可获取电路中是否存在潜在通路[3]。
3.1 连接矩阵
潜在通路的判定算法具体步骤如下:
1)找出需要分析是否存在潜在通路的功能元件以及其转化为有向图中的有向边ei;
2)在一定的开关组合下,使该功能元件使能的路径数目p;
3)按照定理1中的准则求取开关函数Fij;
4)将开关函数Fij中不包含ei的子项去掉,多项式中剩余子项的个数记为q;
5)比较p与q的大小;
若p>q,则存在设计的功能支路被抑制,若p 图2中的某汽车点火电路是存在潜在通路的典型例子,在该电路中,要求在打火开关断开时,收音机不能被触发开启,危险开关和闪光器为旁通设计,刹车开关与刹车灯、停车灯与停车开关构成相应功能支路。 3.2 潜在通路的开关组合 将处理后的开关函数与设计功能数对比,找出开关函数中功能元件被非期望激发的所有子项,将每个子项中的所有开关元件对应的有向边ei设定为闭合状态,电路中的其他所有开关元件都设定为打开状态,这些开关元件所组成的集合即为对应潜在路径下的开关组合。 分析图2中的电路可知,其存在潜在路径ΔF′=e1e2e6e8,该多项式中含有开关元件e1与e6,不含开关e5与e7,因此对应的开关组合为[e1,e5,e6,e7]=[1,0,1,0],其中1代表开关闭合,0代表开关断开。 3.3 潜在通路的改进 在开关电路中,当功能元件被非期望激发时,通过开关函数的子项找出所有潜在路径,在每条导通路径中,从该功能元件开始,沿着电流的反方向找到与该功能元件最近的电气元件,在两个元件之间添加二极管[13],按照二极管正向导通反向截止的电气特性,添加二极管元件后的电路能够抑制该潜在通路并且不会对电路的其他功能造成影响。 利用该方法,对图2中的电路进行改进,得到改进后的电路如图4所示。 图4 改进后的汽车点火电路 规定图4中二极管的功能边为e9,左端点为节点G,则改进后的电路连接矩阵为: (7) 将除去第4行第1列的子矩阵取行列式并将平方项省略,得到改进后电路的开关函数为: F41=e1e2e3+e1e2e4e5+e3e6e7e9+e4e5e6e7e9+e7e8 (8) 关于e8的导通路径函数为ΔF=e7e8,满足p=q=1,因此改进后的电路不存在潜在通路。 利用MentorGraphics公司设计研制的电气线束设计软件CapitalHarnessSystem对图2中的点火电路进行潜在通路分析验证,转化成的电路图如图5所示。 图5 基于CHS的某汽车点火电路图 利用CHS中CapitalSimProve功能模块对图5中的电路图进行定性仿真,电路中存在的潜在通路函数以及对应的开关状态如图6所示,可以看出该电路存在一条潜在通路。 图6 某汽车点火电路潜在通路CHS仿真结果 图7表示用CHS画出的改进后汽车点火电路图,在刹车开关与收音机之间增加一个反向二极管,利用CapitalSimProve进行仿真,仿真结果显示改进后的电路不存在潜在通路,验证了潜在通路改进方法的正确性。 图7 改进后某汽车点火电路图 本文针对传统潜在通路分析的邻接矩阵法不能准确得到潜在通路的具体路径的缺点,提出基于有向图的连接矩阵方法对电路进行潜在通路分析,定性求解出功能元件所有潜在通路的路径信息,在此基础上对潜在路径进行抑制与消除,能从根源上避免潜在路径的形成,在实际工程应用中具有很大的实用价值。 [1] 胡昌华, 陈斌文, 刘丙杰. 复杂系统潜在问题分析理论与应用[M]. 北京:科学出版社, 2008. [2] 卢佩英, 沈士团, 孙宝江. 潜在通路分析在自动测试系统中的应用研究[J]. 计算机测量与控制, 2006,14(7): 847-866. [3] 徐 萍, 马齐爽, 邹 涛. 开关电路潜通路分析的一种方法[J]. 北京航空航天大学学报, 2011, 37(3): 360-363. [4] 黎剑源, 丘东元, 张 波. n阶谐振开关电容变换器潜电路图论分析法[J]. 中国电机工程学报, 2008, 28(3): 53-59. [5] 郑 丹. 流体网络中单向回路问题的研究[D]. 阜新:辽宁工程技术大学, 2004. [6] 刘 剑, 贾进章, 于 斌. 通风网络含有单向回路时的通路算法[J]. 辽宁大学工程技术大学学报, 2003, 22(6): 721-724. [7] 刘丙杰, 刘勇志, 卫 翔. 图论与定性仿真相结合的潜在通路分析[J]. 四川兵工学报, 2009, 30(7): 17-19. [8] 兰家隆, 刘 军. 应用图论及算法[M]. 成都:电子科技大学出版社, 1995. [9] 王桂平, 王 衍, 任嘉辰. 图论算法理论、实现及应用[M]. 北京:北京大学出版社, 2011. [10] 梅 义, 丘东元, 张 波. 基于深度优先搜索的潜在电路计算机辅助分析法[J]. 中国电机工程学报, 2008, 28(24): 75-80. [11] 丘东元, 张 波. 谐振开关电容变换器中潜电路现象的研究[J]. 中国电机工程学报, 2005, 25(21): 34-40. [12] 刘丙杰, 贾兴亮, 赵永刚. 潜在通路存在的判定方法研究[J]. 航天控制, 2009, 27(2): 88-90. [13] 邹 涛, 马齐爽. 基于网络流仿真的潜通路分析方法[J]. 北京航空航天大学学报, 2012, 38(4): 546-550. Sneak Circuit Qualitative Analysis Method Based on Connection Matrix Huang Cong1,Mei Hong2,Zhang Qingzhen1,Cheng Lin1 (1.School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China;2.Beijing Aerospace Automatic Control Institute, Beijing 100854, China) The electrical components were qualitative modeled in the circuit diagram. To get the connection matrix of the circuit diagram, it’s necessary to transform the circuit diagram to directed graph by the current direction on the basis of the modeled components. All the paths in the directed graph from the battery positive terminal to ground could be calculated by using its algebraic cofactor, and compared the paths with the function branches that were designed for the circuit graph. Compared to the adjacency matrix method used in traditional sneak circuit analysis, this method could not only judge whether there were sneak circuits in the circuit graph, but got all the conduction paths information of the sneak circuits. On this basis, the method that was designed for wiping the effects of the sneak circuits was proposed to improve the original circuit graph. The validity and feasibility of the method has been confirmed experimentally in the car ignition circuit by using Capital Harness System(CHS). connection matrix; switch function; sneak circuit analysis; CHS 2016-01-15; 2016-05-24。 黄 聪(1992-),男,湖北黄冈人,硕士研究生,主要从事制导与控制,电气仿真方向的研究。 1671-4598(2016)09-0240-04DOI:10.16526/j.cnki.11-4762/tp TM A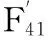


4 CHS仿真验证



5 结论
