双足机器人下楼梯动作的设计与生成

张 勤,邱俊佳,范吉斌

(华南理工大学 机械与汽车工程学院，广州 510641)



双足机器人下楼梯动作的设计与生成

张 勤,邱俊佳,范吉斌

(华南理工大学 机械与汽车工程学院，广州 510641)

上下楼梯是人们典型，常见的动作，研究其动作生成算法是实现稳定步态的重要保证；以双足机器人为研究对象，以下楼梯动作为例，基于重复变换的上体重心移动法提出双足机器人下楼梯动作的设计方法；通过仿真生成了3种典型模式的下楼梯动作过程，评价了下楼梯过程中各关节的角度变化，力矩变化和稳定性，讨论了楼梯参数变化对机器人各关节负担的影响；仿真结果表明，通过改变下楼梯的方式，可以减轻下楼梯对腿部损伤关节的负担，提高安全性，实现稳定的下楼梯动作；为福祉，康复医疗教育提供依据。

双足机器人；下楼梯动作；重复变换法；重心移动

0 引言

随着人们生活水平的提高，人的寿命得到了很大延长。我国和世界上许多国家一样，正在步入老龄化社会。老龄化进程的加速，使康复医疗设施、教育的重要性越来越引起社会的关注。对老年人日常生活动作的运动分析正在成为康复医疗教育、研究、临床等融合学科中不可或缺的重要组成部分。

随着年龄的增长，老年人身体的协调性，柔韧性减弱，关节活动幅度减小，平衡能力下降，导致其站立或行走时会出现晃动不稳的现象，容易发生跌倒事故[1]。特别是下楼梯时的意外摔倒，将会对老年人造成更大的伤害风险。如何减少下楼梯摔倒事故，保证老年人日常生活的安全，具有重要的研究意义。

双足机器人与人体相似，具有相同的运动方式和多自由度的特点，通过对双足机器人下楼梯动作的解析，研究老年人下楼梯动作的安全性，可以为康复医疗教育提供理论依据。

双足机器人具有冗余度，通过其各关节姿势的巧妙组合能够完成各种动作[2]。下楼梯时，机器人左右脚交替支撑，重心位置动态变化，保证双足机器人稳定而不翻倒，动作的生成方法是关键。

关于机器人下楼梯的步态生成方面的研究不多，但也取得了一定的成果。Kim Eun-Su等人以机器人的七连杆模型为对象，通过混合的低阶多项式拟合关节运动的轨迹，提出单变量动态编码算法，实现了机器人上下楼梯的步态规划[3]。陈启军等人建立5质点4杆的被动双足行走模型，通过调整膝关节的弯曲时间设计了模型的屈膝行为，并通过仿真分析了楼梯高度对下楼梯动作稳定性的影响，完成了一定台阶高度下稳定的下楼梯动作[4]。付根平等人基于ZMP误差校正，提出了仿人机器人步行控制方法，保证机器人在外力扰动等环境中的步行稳定性[5]。张奇志等人提出一种足部增加舵机驱动提供冲击力矩的半被动双足机器人控制系统方案[6]。文献[7-9]通过穿戴式传感器获取的人体运动数据，确定上下楼梯时的人体姿态位置与关节轨迹，再通过优化算法进行运动控制，也取得了较好的控制效果，但这种方法对传感器提出了很高的要求。此外还有一些国内外学者对双足机器人上下楼梯动作进行了相关的研究[10-12]。

从以上的分析可以看出，现有的研究一般是以特定的机器人为研究对象，在建模上很少考虑人体模型的重量分配和老年人步态的特点；在算法上主要是关注机器人腿部关节的运动，在预先设定关节轨迹的基础上，通过算法优化，实现步态的规划。在现有研究基础上，本文以老年人下楼梯动作为背景，考虑人体模型特点和重量分配，建立双足机器人的仿真模型，解析下楼梯的动作过程。通过机器人上体的移动调整其重心位置，基于重复变换法对重心的位置逐次评价，逐步更新，满足下楼梯过程中对机器人重心的变化要求。在此基础上考察了典型的下楼梯动作的稳定性和安全性。

1 仿真模型的建立

1.1 双足机器人的建模

考虑人体运动的特点，参照人体模板[13]，建立仿真模型如图1所示。该模型具有8个自由度。每条腿具有3个自由度，腰关节J为球关节，具有2个自由度。左右两腿的关节角度分别表示为θLi和θRi，其中i=(1，2，3)，分别代表踝、膝、髋关节。分别以机器人初始位置时腰关节J和两脚之间的位置O为原点建立参考坐标系∑J，∑O。设各关节转动角度顺时针为正，逆时针为负。

图1 机器人的仿真模型

考虑人体的躯干部分重量占人体总重量的70%以上[14]，为了简化模型，可以忽略下半身的质量，将机器人重心简化在上体的C处。机器人的结构参数设定如表1所示。

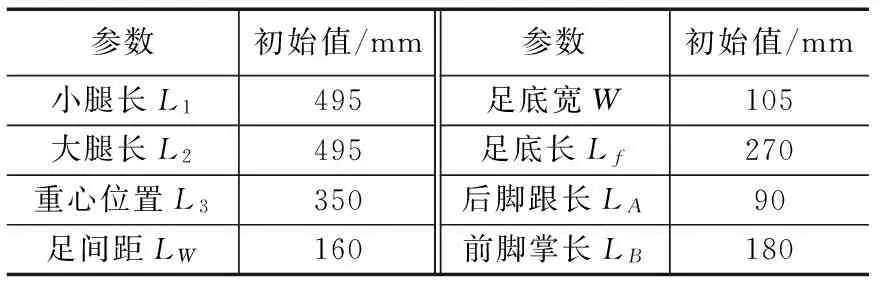
表1 机器人结构参数

考虑老年人缓慢的下楼梯动作，忽略动力学的影响，只考虑静步行。假设腰关节绕xJ轴的转动为φ，绕yJ轴转动为ψ，则重心位置C(x,y,z)在∑J中表示为：

(1)

通过改变腰关节转角(φ,ψ)，可以调节机器人重心C的位置。

考虑人体各关节的结构，损伤等情况不同，各个关节所能承受的力矩和转动角度范围都是有限的，超出关节的承受能力，容易诱发摔倒事件发生。动作生成过程中，关节转动角度越小，所受的力矩负担越小，就越能轻松地完成下楼梯动作。

1.2 稳定性评价及其数学描述

机器人下楼梯过程中，单脚支撑，双脚支撑交替进行，支撑面和重心位置动态变化，要保证稳定的下楼梯动作而不摔倒，必须保证机器人的重心CoG(Center of Gravity)在地面上的投影点CoP(Center of Projection)始终在支撑面内。由支撑脚围成的支撑面区域称之为稳定区域。使用CoP点到稳定区域边界的最小距离，也就是稳定裕度Dt来评价下楼梯动作的稳定性，Dt越大，则表示阻止机器人翻倒的力矩越大，抗干扰能力越强，步态的稳定性越好。稳定区域一般为多边形，下楼梯时如果使用辅助支撑，比如手杖等，则稳定区域将扩大，稳定性增强。

图2表示各种步态下的稳定裕度。假设dx，dy，dj分别为t时刻对应支撑多边形各边法线方向的稳定裕度，则该时刻机器人支撑面上各个方向的稳定裕度的集合表示为{dx,dy,dj, …}，机器人的稳定裕度为：

(2)

其中：

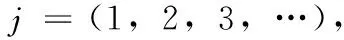
下楼梯过程中，支撑多边形动态变化，稳定裕度集合中元素个数和大小也变化，Dt也随之改变。假设机器人的重心在其支撑面上投影点CoP坐标为(xi，yi)，目标重心点的坐标为(xm，ym)，则两点之间的距离为：

(3)

用式(3)描述每个时刻CoP位置与重心目标点的趋近程度。单脚支撑时，目标重心点在支撑脚的中心，双脚支撑时，目标重心点在两支撑脚中心连线上沿机器人移动方向动态变化。使用辅助支撑时，考虑辅助程度设定目标点位置。

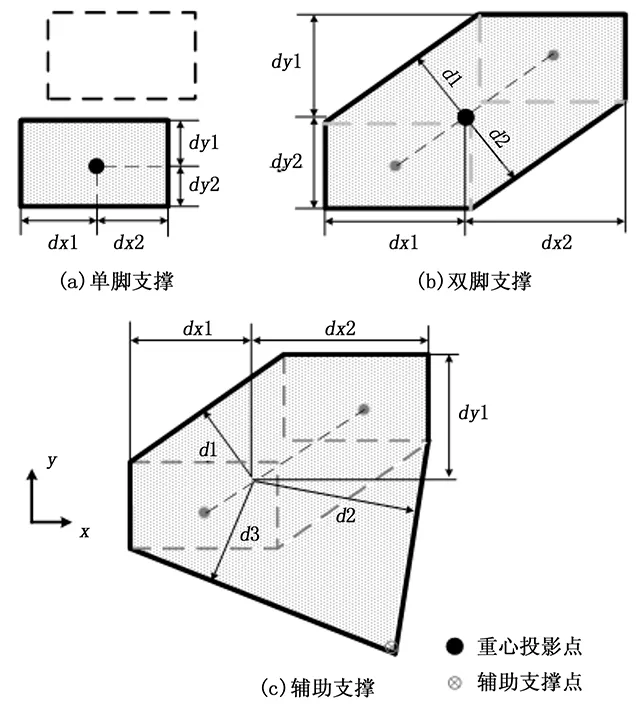
图2 稳定裕度的描述

2 下楼梯动作轨迹生成算法

一步一台阶的下楼梯方式是最常见的下楼梯方法，其动作可以分解为以下几个阶段，如图3所示。

①机器人的重心CoP从初始状态的两脚中间向支撑脚移动(右脚)；

②重心CoP完全移到右脚后，左脚抬起；

③保持重心CoP不变的前提下，支撑腿(右腿)弯曲，使左脚踏到下一台阶上；

④重心CoP从右脚逐渐向左脚移动；

⑤重心CoP完全移动左脚后，左腿和腰伸直，右脚向下一个台阶迈出。

重复上述步骤，左右两脚交替支撑完成下楼梯动作。

上述过程中，机器人重心的移动是关键。通过机器人上体的移动调整其重心位置，满足机器人下楼梯时重心CoG的变化要求。上体重心的移动，基于重复变换法实现。

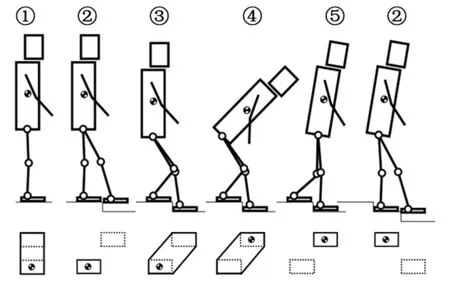
序号①～⑤表示下楼梯动作分解的各个阶段
图3 重心投影和姿态变化示意图

2.1 基于重复变换的上体重心移动算法

机器人下楼梯过程中上体重心的移动，通过腰关节的两个自由度(φ，ψ)来实现。给出腰关节可能的微小转动量，根据式(1)计算出与各关节微小转动相对应的机器人9种姿势，从中优化出满足稳定性要求，符合作业目标的姿态。详细算法叙述如下：

1)设定腰关节的转动范围[φmin，φmax]和[ψmin，ψmax]，机器人的初始姿势和各阶段目标重心点的位置(xm，ym)。

2) 给出腰2个转动关节(φ，ψ)所对应的微小转动(-Δφ，0，Δφ)和(-Δψ，0，Δψ)，将微小转角带入方程(1)，计算与其对应的32种机器人重心C的位置和姿态。

3) 从求得的32种姿态中，选出重心的CoP在稳定区域内，也就是满足机器人不翻倒条件的解，如果满足上述条件的解不存在，则说明目标作业无法实现。

4) 在步骤3)选出的姿势中，根据式(3)求出每种姿势中CoP点位置到目标支撑点(xm，ym)的距离l，选择距离l为最小的机器人姿势，作为当前姿势，返回2)。

上述过程不断循环重复，对重心的位置逐次评价，逐步更新腰关节姿势，满足下楼梯过程中，重心的动态变化要求，生成使机器人既不翻倒，又能满足下楼梯要求的CoP点移动轨迹。

2.2 下楼梯动作的生成算法

假设机器人初期位置的重心在两脚中间，根据3.1的算法将机器人的整体重心移到支撑脚(右脚)中心，另一只脚(左脚)抬起。在机器人的重心位置投影不变(右脚下)的前提下，根据台阶参数(台阶高度和宽度)确定左脚能够跨到下一级台阶时，支撑腿(右腿)各关节的转角θR1，θR2和θR3。通过右腿关节的弯曲，使腰关节的位置下降，保证左脚踏到下一级台阶上。再根据上体重心移动算法，调节腰关节(φ，ψ)，将CoP位置逐渐移动到左脚。然后腰和支撑腿(左脚)逐渐恢复伸直，完成支撑脚的交替。在恢复动作过程中，应尽量保持CoP位置不变(在左脚下)，具体方法是给出左腿关节θLi所对应的微小增量+ΔθLi，(i=1，2，3)，通过支撑腿(左腿)的顺运动学求得重心C的位置，然后基于重复变换法优化出整体重心投影位置CoP基本不变的腰关节的角度，重复上述过程，直到腰部和支撑腿都恢复伸直，完成下台阶动作。下楼梯过程的算法框图如图4所示。

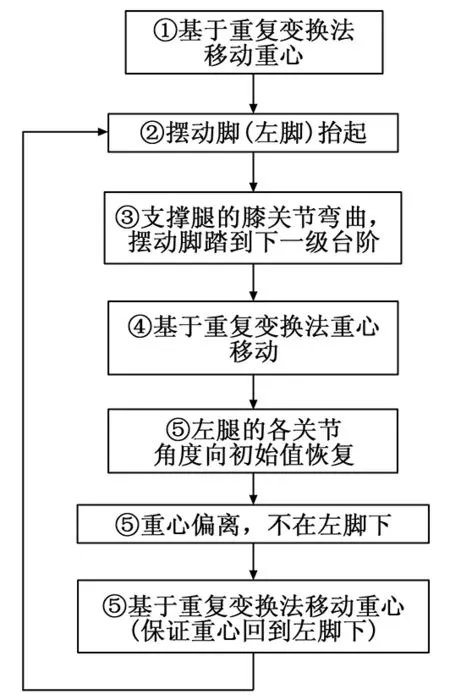
图4 下楼梯动作过程框图

3 仿真事例与稳定性分析

根据上述仿真模型和算法，对机器人下楼梯动作的生成进行仿真。以初始位置的两脚踝之间坐标系∑O为参考坐标系，描述重心在支撑面上的投影。考虑老年人的身体特点，设定ψ的初始值为7.4°，踝关节角度初始值为90°，其他关节角度初始值为0，以腰关节坐标系∑J为参考，描述下楼梯过程中机器人重心C的变化。设定支撑脚的中心位置为重心投影点的目标位置，各关节的微小角度变化为0.2°。通过仿真，分析下楼梯动作过程，考察其动作的稳定性。

3.1 下楼梯动作仿真

考虑标准的楼梯尺寸，设定楼梯的高度Sh=150 mm，楼梯的宽度Sw=280 mm。机器人的质量m=60 kg，其它参数参照表1，考察各种模式的下楼梯动作。一步一个台阶是通常的下楼梯模式：左右两脚交替支撑，完成下台阶动作。完成动作各阶段示意图和支撑面积的变化如图5所示，图中的序号①～⑤对应下楼梯动作分解的各个阶段。其中②③⑤阶段为单腿支撑，①④均为双腿支撑阶段。左右两脚交替支撑，实现机器人的移动，完成下楼梯动作。

图5 一步一台阶下楼梯动作示意图

图6为一步一台阶模式下，机器人腰关节角度，重心位置，腿关节转动角度，转矩等参数随时间的变化。其中图6(a)为腰关节随时间的变化情况，在左右两脚重心移动阶段④，和上体恢复阶段⑤，通过腰关节的运动，调整上体重心位置，满足左右腿交替支撑过程中重心变化的要求，保证了机器人下楼梯动作稳定而不摔倒。图6(b)表示伴随机器人上体移动的其重心位置(x,y,z)的变化。左右腿各关节角度变化如图6(c)所示，其所受力矩如图6(d)所示，可以看出，左右两腿交替支撑，身体向前移动过程中，腿部的髋关节和膝关节承受的力矩较大，且在单脚支撑时，图6(d)中的A，B两点受到力矩最大。重心在支撑面内的投影变化如图6(e)所示，其中灰色部分表示支撑脚围成的区域。从图可以看出，一步一台阶模式下，左右腿交替支撑，负担相同，适用于两腿健康的人群。如果其中一条腿的关节有损伤，可以采用模式2，也就是两步一台阶的下楼梯方式。

图6 模式1各阶段运动参数的变化

假设左腿较弱，在下台阶时，可以总是以右腿支撑，抬动左腿，模式2动作示意如图7所示。对比模式1，①～④阶段相同，主要区别在于阶段⑤。两步一个台阶方式时，重心完全移动到左脚后，右脚移动到左脚旁，与此同时腰关节与左腿的各关节角度向初始值恢复，基于重复变换法使机器人的重心重新恢复到两脚之间。各运动参数如图8所示。由图8可见，下楼梯过程中，左右两腿关节角度变化，受到的力矩并不相同。与模式1相比，下楼梯过程中腰关节，右腿关节的转动角度基本相同，但左腿各关节的转动角度范围变小，膝关节受到的扭矩降低，减轻了左腿的负担，且一个动作周期内双脚支撑的时间相对增加，减少了腿部疲劳。图8(e)为机器人重心在支撑面上投影的轨迹。

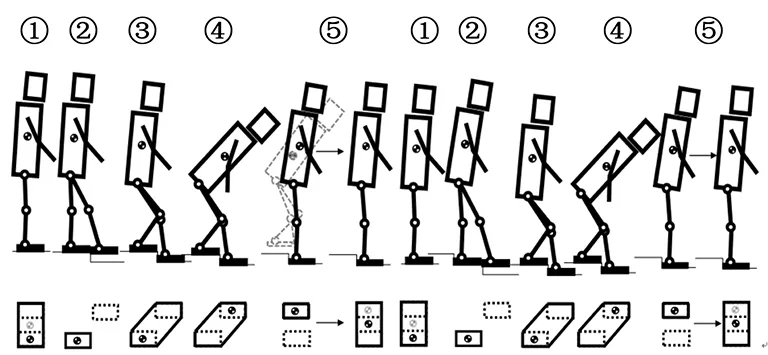
图7 两步一台阶下楼梯动作示意图

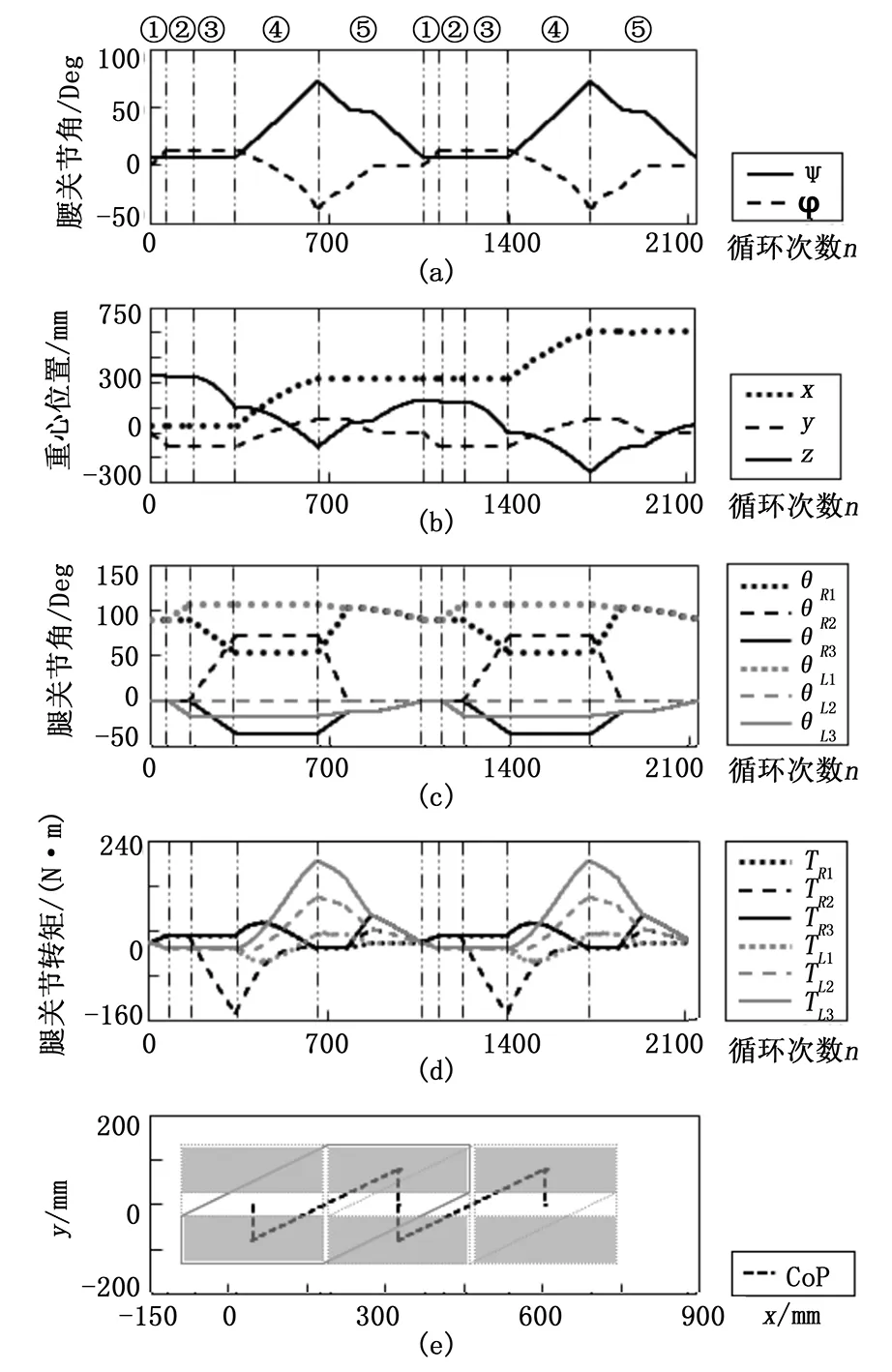
图8 模式2各阶段运动参数的变化

如果左腿损伤严重，下楼梯动作超出其承受能力，可以借助辅助支撑完成下楼梯动作。手杖可将无力或疼痛下肢的重量重新分布，通过增加支撑面面积改善稳定性[15]。一般手杖要置于健足同侧，辅助支撑采用两点步态方法[16]，也就是手杖与患足同时伸出并支撑体重，再迈健足。使用辅助支撑的下楼梯动作(模式3)示意如图9所示。从图9可以看出，下楼梯各阶段支撑多边形动态变化。与模式1和模式2相比，支撑面积明显增大。根据手杖的使用方法[15,17]，假设辅助支撑点距离健足前边缘(足尖)后80 mm，侧边缘100 mm，辅助支撑手杖承受身体重量的10%，按照这个比例设定目标重心位置。仿真结果如图10所示。与模式2相比，腰关节，腿关节转动角度的变化基本相同，由于手杖对左腿的辅助支撑，左腿承受的转矩降低，支撑面积增加，稳定性增强，减轻了患足的负担。图10(e)表示动作过程中，支撑区域的变化。

图9 辅助支撑下楼梯动作示意图

图10 模式3各阶段运动参数的变化

3.2 台阶参数对动作的影响

图11和图12分别表示台阶宽度Sw和高度Sh变化时，一步一台阶下楼梯过程中，腰关节(φ，ψ)，支撑腿膝关节转动角度最大值θR2max，支撑腿各关节力矩最大值TR1max、TR2max和TR3max的变化情况。由图11(a)可见，随着台阶宽度的增加，完成稳定的下楼梯动作，机器人腰关节，腿关节转角范围均增加，承受的力矩也增大。随着台阶高度的增加，图11(b)，对腿部的膝关节的负担加大。因此应尽量避免跨越高度，宽度较大的台阶，以减轻腰关节，腿关节的负担。

图11 台阶宽度Sw变化的影响

图12 台阶高度Sh变化的影响

3.3 结果分析与稳定性评价

根据4.1节的仿真结果可知，无论哪种下楼梯模式，提出的算法均能生成稳定的下楼梯动作。3种下楼梯模式各阶段的稳定裕度如图13所示，由图可见，每种模式中，双脚支撑阶段的稳定裕度明显高于单脚支撑阶段。两步一台阶模式与一步一台阶的下楼梯方式相比，双腿支撑时间长，稳定裕度高；增加辅助支撑后的稳定裕度最高，也就是说，使用辅助支撑后稳定性最好。考虑老年人的身体条件，选取合适的下楼梯方式，可以提高下楼梯动作的安全性。

图13 3种下楼梯模式的稳定裕度

4 结论

本文建立了双足机器人模型，基于重复变换的重心移动法提出了双足机器人下楼梯动作的生成方法。通过机器人上体的移动调整其重心位置，基于重复变换法对重心的位置逐次评价，逐步更新，满足下楼梯过程中机器人重心的变化要求，生成了机器人不翻倒，稳定的下楼梯动作。

考虑老年人肌肉退化，关节僵硬，可动范围变小，平衡能力减弱的特点，对3种模式的下楼梯动作进行了考察。通过仿真详细分析了下楼梯动作过程，评价了下楼梯过程中各关节的角度变化，力矩变化和稳定性，讨论了楼梯参数变化对机器人各关节的影响。仿真结果表明，通过改变下楼梯的方式，可以减轻下楼梯对损伤关节的负担，提高安全性，实现稳定的下楼梯动作。

本研究提出的算法，同样也适用于机器人的各种步态的生成。为福祉，康复医疗教育提供理论依据。

[1] 侯 曼, 侯 佳, 王汉玉. 对60～89岁老年人下肢柔韧性的测试研究[J]. 北京体育大学学报, 2010, 27(1): 57-59.

[2] 张 勤, 吴志斌, 神谷好承. 基于重复变换法的多关节站立型机器人搬运动作仿真[J]. 机器人, 2011, 33(3): 340-346.

[3] Kim E S, Kim J H, Kim J W. Generation of optimal trajectories for ascending and descending a stair of a humanoid based on uDEAS[A].IEEE International Conference on Fuzz Systems[C]. Jeju Island, Korea: IEEE, 2009: 660-665.

[4] An K, Chen Q J. Passive dynamic model for walking down stairs[A].25th Control and Decision Conference(CCDC)[C]. Guiyang, GuiZhou, China: IEEE, 2013: 3166-3172.

[5] 付根平, 杨宜民, 陈建平, 等. 基于ZMP误差校正的仿人机器人步行控制[J]. 机器人, 2013, 35(1): 39-44.

[6] 李 诚, 张奇志, 周亚丽. 半被动双足机器人控制系统设计[J]. 计算及测量与控制, 2015, 23(11): 3651-3653.

[7] Lim I S, Kwon O, Park J H. Gait optimization of biped robots based on human motion analysis[J]. Robotics and Autonomous Systems, 2014, 62: 229-240.

[8] Paola C F, Ruben A, Salim G, et al. Gait event detection during stair walking using a rate gyroscope[J]. Sensor, 2014, 14: 5470-5485.

[9] Yuan Q L, Chen I M, Lee S P. SLAC: 3D localization of human based on kinetic human movement capture[A].IEEE International Conference on Robotics and Automation[C]. Shanghai, China: IEEE, 2011: 848-853.

[10] Matthew J P, Zhao H H, Aaron D A. Motion primitives for human-inspired bipedal robotic locomotion: walking and stair climbing[A].IEEE International Conference on Robotics and Automation[C]. Saint Paul, Minnesota, USA: IEEE, 2012: 543-549.

[11] Park C S, Ha T S, Kim J H, et al. Trajectory generation and control for a biped robot walking upstairs[J]. International Journal of Control, Automation and Systems, 2010, 8(2): 339-351.

[12] 柯显信, 龚振邦, 吴家麒．双足机器人上楼梯步态规划的复现性要求[J]. 应用科学学报, 2003, 21(1): 63-67.

[13] GB/T 15759-1995, 人体模板设计和使用要求[S]. 北京: 中国标准出版社, 1996.

[14] GB/T 17245-2004, 成年人人体惯性参数[S]. 北京: 中国标准出版社, 2004.

[15] Bradley S M, Hernandez C R. Geriatric assistive devices[J]. American Family Physician, 2011, 84(4): 405-411.

[16] 邱启祥, 王小敏, 刘 浩. 助行设备在美国老年人群中防跌倒作用的现状分析[J]. 中国康复理论与实践, 2014, 20(1): 85-87.

[17] 朱卫娟, 王 彤．不同步行辅助器对健康人负重影响的分析[J]. 中国伤残医学, 2010, 18(5): 109-111.

Action Design and Generation of a Biped Robot Descending Stairs

Zhang Qin, Qiu Junjia, Fan Jibin

(School of Mechanical& Automotive Engineering, South China Univ. of Tech., Guangzhou 510640, China)

As ascending and descending stairs are typical and common actions of human, it is essential to study the algorithm of action generation of walking stairs so that steady gait can be solidly performed. Taking biped robot as research object, and descending stairs motion as example, an action generation approach based on upper body gravity move method under the principle of repeatedly direct kinematics(RDK), is proposed. Through simulating three typical modes of descending stairs, variations of angle and torques at each joint and the stability of this approach are evaluated. Also the impact of stair parameters on load of robot’s joints is discussed. The simulation shows that changing the modes of descending stairs can reduce load on injured leg joints, improve safety, and achieve stable action of descending stairs. The result provides a basis for health care and medical education.

biped robot; descending stairs action; repeatedly direct kinematics(RDK); gravity move

2016-03-26；

2016-04-18。

广东省部产学研项目(2012B091100145)；广东省科技计划项目(2014A020208018)。

张 勤(1964-)，女，辽宁锦州人，博士，教授，主要从事机器人及其应用系统研究。

1671-4598(2016)09-0218-06

10.16526/j.cnki.11-4762/tp.2016.09.061

TP242

A