主成分分析与遗传神经网络在制冷系统故障诊断中的应用

张 琪，吴亚锋，徐 建

(1.中国华阴兵器试验中心 环境模拟室，陕西 华阴 714200；2.西北工业大学 动力与能源学院，西安 710072)



主成分分析与遗传神经网络在制冷系统故障诊断中的应用

张 琪1，吴亚锋2，徐 建1

(1.中国华阴兵器试验中心 环境模拟室，陕西 华阴 714200；2.西北工业大学 动力与能源学院，西安 710072)

针对低温试验系统制冷设备测点多、数据间存在强相关性等特点，将主成分分析法和遗传神经网络智能识别方法进行组合，引入制冷系统的故障诊断中;结合专家经验和主成分分析客观地对多传感器信息进行了科学合理的故障特征优选，从而确定了神经网络的输入空间;为了克服神经网络易陷入局部最小的缺陷，利用遗传算法的全局搜索能力，对神经网络的初始权值和阈值进行了优化;运用该方法对制冷系统各故障状态进行识别，结果表明，简洁有效的网络结构不仅缩短了训练时间，而且提高了网络的稳定性和分类精度，为监测系统提供了一种有效的故障诊断方法。

故障诊断；主成分分析法；遗传神经网络；MATLAB

0 引言

由于低温模拟试验系统设备组成复杂,任务负荷大,温控要求高,其设备安全可靠的运行至关重要。制冷设备一旦出现故障，将造成巨大的经济损失和社会影响。因此需要对系统设备实时开展故障诊断，及时监测设备的运行状况，识别故障早期征兆，对故障部位、故障程度和发展趋势做出准确判断， 以实现设备的预知性维修，即由计划维修向状态检修过渡，提高机组的可靠性和可利用率。

故障诊断的本质是对工况状态模式的识别过程。神经网络作为模式分类器应用非常普遍，其强大的自学习机制能够实现输入和输出之间的非线性映射。误差反向传播的前馈型网络(BP)是神经网络中最精华的部分，应用于实例的神经网络约80%～90%都采用了BP网络或它的变形。由于神经网络具有自身容易陷入局部最小的缺陷，有必要利用遗传算法的全局搜索能力对网络的连接权值与阈值进行优化，改善网络识别的稳定性和精度。针对实际状态、特征信息种类多，强关联的特点，应用主成分分析法(PCA)提取出可反映样本绝大部分信息的少数相互独立的综合变量。本文结合PCA和GABP网络的优点，将控制系统测量信息作为输入，9个典型故障类型作为输出，仿真结果表明，该组合算法结构简洁，识别速度快，分类精度较高。

1 主成分分析法

1.1 主成分分析法的基本思想

由于模式识别方法的日益成熟，识别精确的关键很大程度上取决于从原始数据中提取的特征变量。为了降低计算的复杂性，避免海量数据引起的效率低下、高维特性导致的维数灾难问题和非线性特性带来的线性模型失效问题等，对原始数据进行降维是很有必要的。主成分分析正是利用降维的思想，研究原始变量相关矩阵的内部结构，找出几个综合指标，综合指标是原来变量的线性组合。在故障诊断中，不同故障表现出的部分征兆可能是相同的，多种征兆的强相关性使得诊断结果准确性不能得到保证。通过对输入故障征兆的降维，去除冗余信息，降低数据间的相关性，使得不同类特征的类间距离最大，同类特征的类内距离最小，对这一特征更敏感。其优点在于实现了可观的数据压缩，降低了对通信带宽和数字信号处理器的要求，有利于实时处理。

1.2 主成分分析法的代数和几何意义

主成分分析是一种多元统计分析方法。通过把高维信息投影到低维子空间，并保留其主要过程信息。具体方法是借助一个正交变换T，将其分量相关的原随机向量x=(x1,x2,…,xp)T,转化成其分向量不相关的新随机向量u=(u1,u2,…,up)T,这在代数上表现为将x的协方差阵变换成对角形阵，在几何上变现为将远坐标系变换成新的正交坐标系，使之指向样本点散步最开的p个正交方向，以一个较高的精度转换成低维度变量系统。根据数据变化的方差大小来确定变化方向的主次位置，按主次顺序得到各个彼此独立主成分。为了便于理解，在二维空间中进行说明。

假设有n个样本，每个样本包含2个观测量x1和x2，在x1、x2所确定的二维平面中，n个样本点的散步情况如图1所示。

图1 x1和x2坐标系下样本点的分布

从图1可知，这n个样本点在坐标轴的任意方向上都具有很大的离散性，如果仅考虑x1和x2中的一个，则会损失很多原始数据的信息。通过同时把x1和x2轴逆时针旋转θ角度，从而得到坐标轴y1和y2,如图2所示。旋转的主要目的是令n个样本点在y1轴方向最大程度的离散，此时，y1的方差达到最大，新变量包含了原始数据的绝大部分信息(譬如方差贡献率85%以上)，在研究问题时可以不考虑y2，两个变量缩减成一个，降维简化了问题。

图2 y1和y2坐标系下样本点的分布

根据旋转公式:

y1=x1cosθ+x2sinθ

y2=-x1sinθ+x2cosθ

我们看到新变量y1和y2是原变量x1和x2的线性组合，它的矩阵表示形式为:

其中:U′为旋转变换矩阵，是正交矩阵，即有U′=U-1，U′U=I。

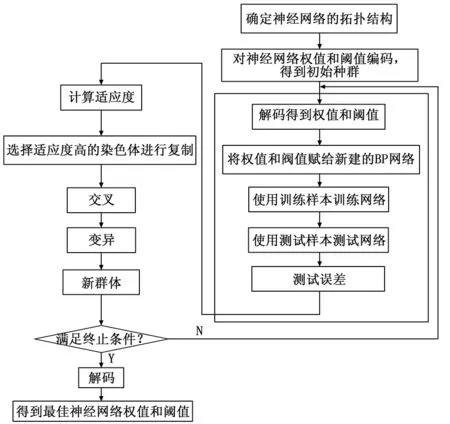
主成分分析法在实际问题的应用中，设某个控制过程有p个变量，如果系统状态可以由指标中的k个主分量(k

1.3 主成分分析的数学模型

在实际问题中，常见的情况如n个样品p个变量x1,x2,…,xp,原始数据矩阵为：

(1)

为了使采集到的不同量纲的多源数据它们具有可比性，先对原始数据进行标准化处理，使得每个变量均值为0，方差为1。常用的标准化方法是z-score标准化:

(2)

协方差CX为:

(3)

计算CX的特征值λ1, λ2,…,λp和对应的归一化特征向量U1, U2,…Up:

(4)

式中，Uj=[u1j, u2j,…, unj]T。设特征值λ1≥λ2≥…≥λp，则yj=UjTX(j=1,2,…,p)即为输入矩阵在特征向量下的投影，就是X的j个主分量。这样就将x=(x1,x2,…,xp)’的p个变量转换成p个新的综合变量了，新变量yj可有原变量x1,x2,…,xp线性表示，即：

(5)

系数uij的确定原则为：

(1)yj与yij(i≠j;i,j=1,2,…,p)相互无关；

(2)y1为x1, x2,…xp一切线性组合中方差最大者；y2为与y1不相关的x1, x2,…xp的所有线性组合中方差最大者；yp为y1,y2,…, yp-1都不相关的x1, x2,…xp所有线性组合中方差最大者。

按以上方法确定的综合变量y1,y2,…yp分别称为原变量的第1, 第 2,…,第p个主成分。并且y1在总方差中所占比例是最大的，其余y2,y3,…yp的方差在总方差中所占比例依次递减。主成分的个数选取由主成分的累积方差贡献率决定，累计贡献率越大，说明保留原始的数据信息越多，通常累积方差贡献率大于80%以上即可。

累积贡献率定义为：

(6)

当累积贡献率大于85%时，将前L个特征向量u1, u2,…, uL构成的低维空间作为投影空间，将原始变量投影得到新的综合变量，至此完成原数据降维处理。这种选择几个方差最大的成分，以达到简化结构，抓住问题实质的目的。

2 遗传神经网络

2.1 BP神经网络与遗传算法结合的动因

人工神经网络是数据驱动的故障诊断中普遍和灵活的机器学习工具，是现代数据分析中的热点，可以处理“黑箱”这类非线性辨识问题。神经元的广泛互联与并行工作使整个网络呈现出高度的非线性特点。网络可以高度自适应地学习和记忆各输入量和输出量之间的关系，学习对象是网络输入层的大量样本，通过对各层的神经元进行训练，在以网络输出均方误差最小的训练目标下，连接权重和阈值不断被调整到最佳值，最终将知识以权值和阈值的形式储存于网络中，以此进行新样本的状态识别。前馈型网络(BP)利用误差的反向传播逐步调整到网络的最佳状态。

遗传算法(GA)在工程问题中，染色体对应的是数据或数组，通常是由一维的串结构数据来表示，串上各个位置对应基因的取值。基因组成的串就是染色体，或者称为基因型个体。一定数量的个体组成了群体。群体中个体的数目称为群体大小，也称为群体规模。而各个个体对环境(评价准则，如最小均方误差)的适应程度叫做适应度。神经网络和遗传算法这两种智能算法都是模拟生物结构去表达输入输出之间隐性关系的。虽然神经网络具有结构简单，可调整参数多，训练算法多，可操作性好的特点，但其自身也存在缺陷，由于搜索求解算法是沿梯度下降的，导致网络存在收敛速度慢的缺点，难以保证复杂网络的全局优化而易导致陷入局部极小值，加之无法准确获得网络结构、初始连接权值和阈值，而它们却是影响网络训练效果的主要因素。因此，有必要采用遗传算法对神经网络进行优化。

2.2 遗传算法与神经网络的结合过程

遗传算法优化BP神经网络是为了得到最佳的网络连接权值和阈值，其原理是把网络的初始权值和阈值作为染色体，建立种群，利用生物遗传特性(复制、交叉、变异)逐代进行选择，高收敛精度与速度保证了搜索到全局范围内的最优解。这个最优解就是最佳的网络结构，比用经验和试验判断更能使网络参数合理化，它的交叉因子和变异因子在网络陷入局部极值时能很好地跳出来，从而克服网络陷入局部最小的缺点，提高网络的学习精度。遗传BP神经网络(以下简称GABP)算法的流程如图3所示。

图3 遗传算法优化神经网络算法流程

该组合算法由三部分组成：BP神经网络结构确定、权值与阈值的遗传优化、网络训练及仿真。根据样本的输入和输出参数的个数来确定BP神经网络拓扑结构，进而得出遗传算法待优化参数的数目，也就能计算出种群中个体的编码长度，染色体长度s=R×s1+s1×s2+s1+s2(R,s1,s2分别为输入层，中间隐含层和输出层的神经元个数)，并编码成二进制形式。交叉概率和变异概率这两个关键的遗传参数是根据适应度的大小进行选择的。训练网络的第一步需要初始化参数，获取一组随机数，这个参数是影响网络训练的重要因素，但是随机的通常不准确，为了得到最佳的权值和阈值，运用遗传算法对训练过程进行优化。遗传算法按照其染色体的复制、交叉、变异原则调整网络的连接权值和阈值，计算出BP网络输出与测试目标的均方误差E：

(7)

(Ok,Tk分别为输出层输出和目标值)，进而得到遗传进化的适应度，向着适应度增大(即网络输出误差最小)的方向在进化代中搜寻最优的个体，即使网络的均方误差最小的权值和阈值。将全部样本按步骤让网络学习一遍后，训练结束的条件是全部样本的输出误差均小于设定的误差精度，如果未达到，网络将继续学习,以相同的条件判定是否结束，最终得到最优的权值与阈值输入网络进行识别。

3 主成分分析法与遗传神经网络结合在制冷系统故障诊断中的应用

3.1 故障样本的获取

低温制冷系统大多故障过程属于缓变故障，温度、压力、流量、转速等多种信号具有变化缓慢、频率较低、波形没有剧烈起伏的特点，设备从正常运行到故障征兆出现再到故障灾害发生是一个较慢的过程，这个故障征兆累计过程中大多数状态量是连续变化的。

核心设备涡轮出现故障将是系统故障的顶事件，很多原因能够引起顶事件的发生，即制冷系统制冷量不足或不能制冷，而且几种征兆往往同时出现，目前常用且成熟的诊断方法是基于各种故障所对应的征兆。进行诊断时，按照由专家经验和系统机理制定的数据统计处理规则，将从设备运行中采集到的各种信号提取特征信息，从而获得故障的相关征兆，利用此征兆进行诊断是否故障和哪类故障。

3.2 主成分分析法的制冷系统故障特征提取

依据制冷系统典型故障域特征向量，利用SPSS数据分析软件进行主成分特征提取。具体分析结果如下。

1)提取特征值及主成分个数：

如表1所示，λ1=13.792，λ2=11.302，λ3=8.164，λ4=5.955，λ5=5.197，λ6=2.516，λ7=1.950，λ8=1.125，λ9=λ10=，…，=λ50=0，可以看出，前8个因子特征值大于1，且它们的累积方差贡献率几乎达到了100%，符合了达到85%以上的提取要求，可以认为这8个因子包含了大部分的信息。这与主成分碎石图的分析结果相吻合。

表1 各成分特征值、方差贡献率及累计方差贡献率

2) 生成新变量：

上述确定了前8个特征值作为制冷系统故障体系的主要因素，而相应的主成分成份矩阵即表达了新的影响因子Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8与原始变量之间的关系，即新的故障模式样本表2所示。

图4 主成分分析碎石图

根据该矩阵写出新变量表达式：

Y1=0.389X1-0.450X2-0.450X3+0.389X4+0.389X5+0.389X6+0.853X7+0.943X8+0.376X9+0.376X10+…-0.443X49-0.450X50

Y2=-0.065X1+0.747X2+0.747X3-0.065X4-0.065X5-0.065X6-0.008X7+0.062X8+0.517X9+0.517X10-0.705…-0.705X49+0.747X50

表2 提取成分荷载矩阵成份矩阵a

.

.

.

Y8=-0.750X34+0.750X35

3.3 基于GABP神经网络的状态故障诊断网络建模

网络输入是被测对象的故障征兆特征值，输出是该状态对应的故障模式。下面对制冷系统分别用BP网络和PCA-GABP网络建模进行故障识别。前者根据制冷系统典型故障论域特征向量选取50个征兆参数A={A1,A2,…,A50}作为BP网络的输入，以9类故障Ci(i=1,2,…,9)作为输出，经验证，这里取隐含层节点数为17，BP网络结构50×17×9。PCA-GABP网络的结构与GABP网络仅区别于输入层节点数不同。由3.2节可知，表征低温系统状态的征兆参数有8个，即网络输入节点数目为8，PCA-GABP网络结构为8×13×9。遗传算子染色体长度分别为1029和243，种群大小和遗传代数分别设定为50和100。输出变量是故障模式代号，用布尔值串表示。如第3种故障C3就是T=[001000000]。隐含层和输出层神经元传递函数均采用S型函数，分别为S型正切函数tansig和S型对数函数logsig；网络训练函数取trainlm，并调用遗传算法工具箱优化初始值对网络进行训练，可提高网络的稳定性和训练速度。训练目标0.01，自学习率0.08，训练次数5 000次。

待检状态样本1：低温试验系统在降温过程中,测控系统测得的制冷系统运行状态为:1号涡轮转速超高、2号涡轮转速超高1号涡轮膨胀机出口温度降低、2号涡轮膨胀机出口温度降低、回冷器冷侧进口温度升高、低温室室内压差为0、低温室回气阀位增至全开等。其故障论域的特征向量可表示为：test1=[00000000001100001111001100111001000000000000000010]。

待检状态样本2：低温试验系统在保温过程运行中发现如下症状：水冷器进出水温差小、水冷器出口气体温度高、空冷器热侧出口气体温度高、涡轮膨胀机进口温度高、1号涡轮压气机出口温度高、2号涡轮压气机出口温度高、回冷器冷侧进口温度升高。其故障论域的特征向量可表示为：test2=[00000000000000000000001110000000000000001001001010]。

由上述主成分分析法进行特征优选，得到降维约简后的特征向量：P_test1=[-4.9752 -4.6545 5.6303 3.1172 1.2140 1.6260 0.0000 0.0000];P_test2=[-2.5208 2.7679 0.4479 1.1261 -1.8676 2.9149 0.0000 0.0000]。

3.4 网络训练与测试

PCA-GABP网络的训练：按照上面设计的网络参数进行训练，训练过程如图5所示。

图5 PCA-GABP网络训练过程

由图5可以看出：PCA-GABP网络达到了较高的网络性能要求，但在训练过程中发现，PCA-GABP网络的稳定性明显高于BP网络，且缩短了训练时间。

网络测试：训练好网络后，分别将P_test1和P_test2作为测试输入向量，对网络进行仿真测试，识别结果如表3所示。

表是实例1和实例2经过两种网络测试结果。实例1中两种网络的识别结果均显示是第9种故障，即试验室密封不严密，这与实际情况相一致。实例2中均显示是第6种故障，即水冷器冷水侧壁面结垢严重换热效率低，也是正确的。通过比较可以得出，这两种网络均能够识别出故障，但PCA-GABP网络的输出隶属度稍高，提高了网络的识别精度。

4 结论

本文提出的主成分分析法与GABP神经网络组合的诊断方法，在保证网络的识别精度不变的前提下，能够消除变量间的冗余信息，简化GABP网络结构，缩减网络训练时间，是实时在线监测的有效方法。利用这一网络可以在很短的时间内诊断出故障，以便于操作人员及时做出应对处理。

表3 PCA-GABP和BP网络对实例1与实例2的测试结果

[1]AbhijitSPandya,RobertBMacy. 神经网络模式识别及其实现[M].徐 勇，荆 涛,等译. 北京：电子工业出版社，1999.

[2] 陈建宏，刘 浪，周智勇，等. 基于主成分分析与神经网络的采矿方法优选[J]. 中南大学学报，2010,41(5):1967-1972.

[3] 周开利，康耀红. 神经网络模型及其MATLAB仿真程序设计[M]. 北京：清华大学出版社，2005.

[4] 陈 明.MATLAB神经网络原理与实例精解[M]. 北京：清华大学出版社，2013.

[5] 徐 磊. 基于遗传算法的多目标优化问题的研究与应用[D]. 长沙：中南大学，2007.

[6] 史 峰，王 辉，等. 智能算法30个案例分析[M]. 北京：北京航空航天大学出版社，2011.

[7] 韩晓娟. 多源信息融合技术在火电厂热力系统故障诊断中的应用研究[D]. 北京: 华北电力大学，2008.

[8] 蒋一然. 基于遗传神经网络的柴油机故障诊断技术研究[D]. 大连：大连海事大学，2009.

[9] 李向前. 复杂装备故障预测与健康管理关键技术研究[D]. 北京：北京理工大学，2014.

Application of Principal Component Analysis and Genetic Neural Network in Fault Diagnosis of Refrigeration System

Zhang Qi1，Wu Yafeng2，Xu Jian1

(1. Department of Environment simulation, Huayin Ordinance Test Centre, Huayin 714200, China 2. School of Power and Energy, Northwestern Polytechnical University , Xi’an 710072, China)

According to the characteristics of data measured from refrigeration equipment in low temperature test system, such as a huge number of points, a strong correlation between the data, genetic neural network combined with principal component analysis (PCA) is introduced into fault diagnosis in the refrigeration system. With the knowledge of expert experience and PCA, the fault feature is extracted from multi sensor information in a scientific and reasonable way, so the input space of the neural network is fixed. The defects of neural network is easy to fall into the minimum in local space, but genetic algorithm(GA) has global search ability, aim at eliminating the defects, GA is used to optimize the initial weights and thresholds of neural network. Using the method into the fault state identification of the refrigeration system, it showed that the simple and effective network structure not only shorten the training time, but also improve the network stability and classification accuracy, so it provides an effective method of fault diagnosis for the monitoring system.

fault diagnosis; principal component analysis; genetic neural network; MATLAB

2016-02-27；

2016-04-18。

张 琪(1984-)，女，陕西咸阳人，硕士研究生，工程师，主要从事故障诊断与预测方向的研究。

吴亚锋(1966-)，男，陕西渭南人，博士研究生导师，主要从事信号与信息处理方向的研究。

1671-4598(2016)09-0023-05

10.16526/j.cnki.11-4762/tp.2016.09.007

TP391.5

A