一种有效的分段光滑信号逼近方法

陈 伟

(江南大学数字媒体学院,江苏无锡 214122)



一种有效的分段光滑信号逼近方法

陈 伟

(江南大学数字媒体学院,江苏无锡 214122)

传统的Fourier变换, 连续小波变换等方法在逼近具有分段光滑特性的非连续信号时, 因Gibbs现象的干扰会产生比较大的误差. 本文提出了一种有效的分段光滑信号逼近方法. 首先根据给定信号的分段点位置, 构造一组标准正交分段多项式系, 该函数系具有正交性, 收敛性及再生性. 然后将信号在该函数系下进行正交分解及重构, 即可得到该信号的最佳平方逼近结果. 数值实验表明, 本文方法比传统的正交基具有更好的逼近结果.

分段光滑信号；逼近；Gibbs现象；正交表达

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.033

1 引言

正交变换在信号的逼近, 压缩, 特征提取等领域具有广泛的应用, 它的数学基础便是正交函数系. 常见的正交函数系, 如Fourier变换中的三角基, 多项式空间中的Legendre基, Chebyshev基以及多种小波函数等, 它们都是连续的甚至光滑的. 然而, 这些正交基并不适合表达分段光滑信号(即非连续信号), Gibbs现象(Gibbs现象：用有限项Fourier级数表达间断信号时, 在间断点处会出现波动, 并且这种波动不能因求和的项数增大而彻底消失).便是其障碍之一. 事实上, 只要是连续的正函数系, 其有限个基函数的线性组合不可能表达间断函数. 实际应用中, 不可能采用无限计算. 那么, 如果要表达间断信息, 只有采用非连续的函数才有可能. 因此, 为了将正交变换理论引入非连续信号处理中, 正交分段多项式函数系(orthogonal piecewise polynomial system, OPPS)便是一种有效的方法.

OPPS的研究可以追溯到Haar函数[1]和Walsh函数[2], 它们都是零次多项式. 上世纪八十年代初, 齐东旭与冯玉瑜建立了L2[0,1]上的一类完备OPPS[3], 命名为U-系统. 作为Walsh函数向高次推广的结果, U-系统是一类真正意义上的OPPS, 也是一类预小波(prewavelet)[4]. 此后, 文献[5,6]分别构造了与U-系统几乎等价的OPPS. 2007年, 在U-系统的基础上, 文献[7]提出了另一类OPPS, 称之为V-系统, 它是一类有限区间上的多小波[8]. U-系统与V-系统在复杂几何信号处理中得到广泛的应用[9～13].

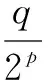
在本文中, 我们提出了一种新的OPPS的构造方法. 根据给定的区间[0,1]上的非均匀层次嵌套剖分, 首先定义一组线性无关函数组, 该函数组中的基为截断单项式. 我们证明了, 当对这组截断单项式进行Gram-Schmidt正交化后, 结果即为对应非均匀节点下的OPPS, 它具有正交性, 再生性及收敛性等性质.

2 非均匀层次嵌套剖分

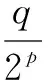
(1)Jn=2n.

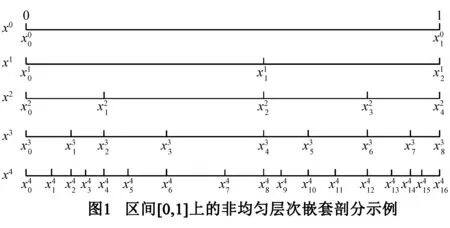
图1显示了当n=1,2,3,4时的某一组非均匀层次嵌套剖分.

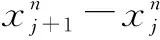
3 非均匀OPPS

3.1 截断单项式及其性质

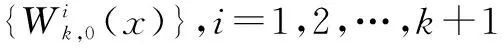
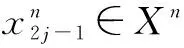
那么,

称为Xn上的截断单项式函数系.

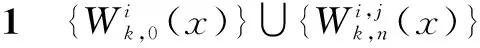
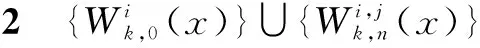
证明 由引理1及Vn的定义即得证.

3.2 非均匀正交分段多项式系的构造

证明 将线性无关函数中的函数按序排列并记为W1,W2,…,Wj,…,相应的正交化结果记为G1,G2,…,Gj,…,而非均匀OPPS的基函数为V1,V2,…,Vj,….

当j=1时,可具体验证G1=W1=V1.

当j=2时,可具体验证G2=W2=V2.

假定G1=V1,对j=1,2,…,m-1(m≥4)成立,根据Gram-Schmidt正交化手续,

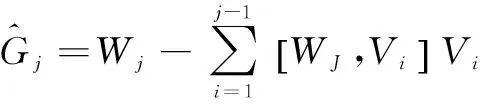
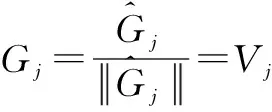
我们将证明上述事实对j=m时也成立.

因此,

而由于

因此

于是

从而

3.3 非均匀OPPS的性质

本文提出的非均匀OPSS具有若干良好的性质，限于篇幅，这里不加证明地列出它的性质,这些性质是对信号进行有效逼近的保障.

(a)标准正交性：k次非均匀OPPS是L2[0,1]上的标准正交函数系,即

(b)平方收敛性：若f(x)∈L2[0,1],则

(c)一致收敛性：若f(x)∈C[0,1]，则

(d)再生性：设f(x)是区间[0,1]上的分段k次多项式函数,且分段点位于Xn{0,1},则f(x)可以用Xn上的k次非均匀OPPS的有限项基函数线性组合表示,即

Λ为有限的指标集.

3.4 分段光滑信号的非均匀OPPS逼近算法

设f(x)的数学表达式如下:

那么,f(x)的非均匀OPPS逼近过程如下:

Step 1 根据定义1及定理1,构造Xn上的k(k≥1)次OPPS.k的取值可由f(x)的复杂程度与逼近精度决定,k的取值越大,逼近精度越高,一般情况下k取3或4已足够.此时OPPS共有2n(k+1)个基函数,记为V0(x),V1(x),…,V2n(k+1)-1(x).

那么,g(x)即为分段光滑信号f(x)的非均匀OPPS逼近结果.当f(x)为Xn上的分段k次多项式函数,此时g(x)实现了对f(x)的精确逼近,即误差为零.

4 数值实验

4.1 分段光滑信号逼近

例1 设f1(x)为定义在[0,1]区间上的一个非均匀分段3次多项式函数,表达式如下:

f1(x)=

第三步,得到逼近结果:

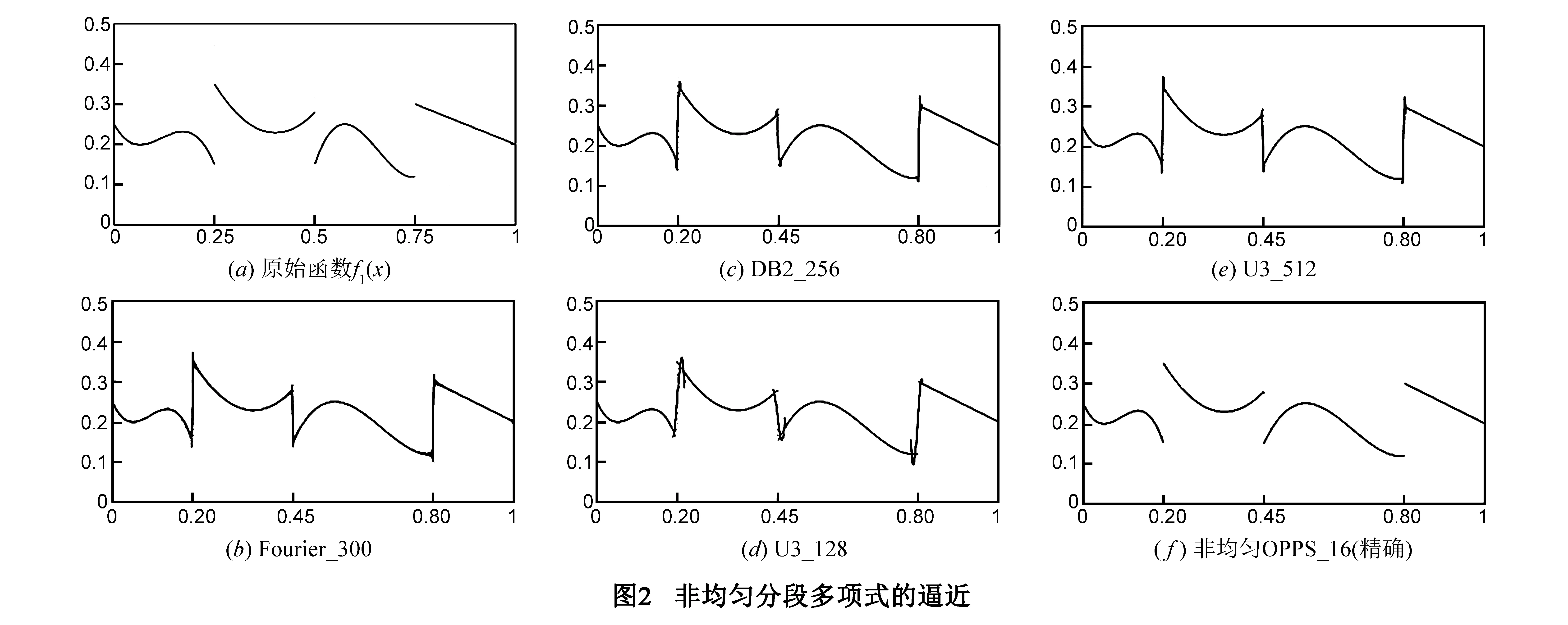
可以看出,g1(x)是对f1(x)的精确重构,如图2(f)所示,该结果也验证了再生性.

例2 设f2(x)为定义在区间[0,1]上的一个非均匀分段光滑函数,表达式如下:

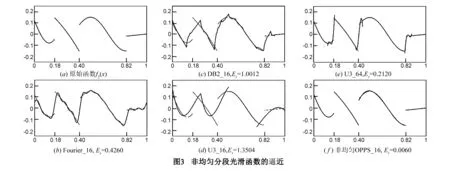
f2(x)的图像见图3(a).为了定量计算逼近误差,用1024个采样点统计近似误差,即

其中,Sn(f2)表示前n项逼近的结果.使用Fourier，DB2小波与3次U-系统进行逼近的结果及误差见图3(b)～(e).最后,我们用3次非均匀OPPS逼近f2(x).计算过程与例1一样,此不累述.这里只列出逼近系数αi,i=0,1,…,15及逼近结果g2(x)的数学表达式.图3(f)显示了逼近结果图像及误差.可以看出,利用本文提出的非均匀OPPS逼近算法,逼近效果有了较大的提高.

5 结论

现有的正交分段多项式函数系(OPPS)定义在有限区间上的均匀剖分节点上,这种固定的内在结构决定了它们在表达非均匀分段信号时的结果是不理想的.本文提出了一种非均匀OPPS的构造方法,它能根据给定的非均匀层次嵌套剖分,自动高效地得到相应的非均匀OPPS.该函数系具有正交性,完备性,再生性及收敛性.数值实验表明,本文方法比传统正交函数系在分段光滑信号逼近中具有更好的结果.

[1]Harr A.Zur theorei der orthogonalen funkionen systeme[J].Mathematische Annalen,1910,69(3):331-371.

[2]Walsh J L.A closed of normal orthogonal functions[J].American Journal of Mathematics,1923,45(1):5-24.

[3]Feng Y Y,Qi D X.A sequence of piecewise orthogonal polynomials[J].SIAM Journal on Mathematical Analysis,1984,15(4):834-844.

[4]Micchelli C,Xu Y S.Using the matrix refinement equation for the construction of wavelets on invariant sets[J].Applied and Computational Harmonic Analysis,1994,1(4):191-401.

[5]Alpert B K.A class of bases in L2for the spares representation of integral operators[J].SIMA Journal on Mathematical Analysis,1993,24(1):246-262.

[6]Beam R M,Warming R F.Multiresolution analysis and supercompact multiwavelets[J].SIMA Journal on Scientific Computing,2002,22(4):1238-1268.

[7]Song R X,Ma H,Wang T J,et al.Complete orthogonal V-system and its applications[J].Communications on Pure and Applied Analysis,2007,6(3):853-971.

[8]Huang C,Yang L H,Qi D X.A new class of multi-wavelet bases:V-system[J].Acta Mathematica Sinica,2012,28(1):105-120.

[9]齐东旭,陶尘钧,宋瑞霞，等.基于正交完备U-系统的参数曲线图组表达[J].计算机学报,2006,29(5):778-785.

Qi D X,Tao C J,Song R X,et al.Representation for a group of parametric curves based on the orthogonal complete U-System[J].Chinese Journal of Computers,2006,29(5):778-485.(in Chinese)

[10]蔡占川,孙伟,齐东旭.基于正交完备U-系统的图形分类与识别方法[J].软件学报,2006,17(Supplement)：21-27.

Cai Z C,Sun W,Qi D X.A Classification and recognition method for planar figures based on complete orthogonal U-System[J].Journal of Software,2006,17(Supplement):21-27. (in Chinese)

[11]熊刚强,齐东旭,郭芬红.一类完备的正交分段多项式函数系及其应用[J].中国科学:信息科学,2012,42(1):70-82.

Xiong G Q,Qi D X,Guo F H.A class of orthonormal complete piecewise polynomial systems and applications thereof[J].Scientia Sinica Informationis,2012,42(1):70-82.(in Chinese)

[12]Song R X,Zhao Z X,Wang X C.An application of the V-system to the clustering of cherno faces[J].Computers and Graphics,2010,34(5):529-536.

[13]Song R X,Yao D X,Wang X C,et al.Retrieval method for 3D object group based on V-system[J].Journal of Advanced Mechanical Design,System and Manufacturing,2012,6(3):340-353.

陈 伟 男，1986年1月出生于江苏省宝应县.2013年获得澳门科技大学理学博士学位，现为江南大学数字媒体学院讲师，主要研究兴趣为小波分析和计算机图形学.

E-mail:wchen-jdsm@163.com

An Efficient Approximation Method for Piecewise Smooth Signal

CHEN Wei

(SchoolofDigitalMedia,JiangnanUniversity,Wuxi，Jiangsu214122,China)

The truncating Fourier and continue wavelet representation of a discontinuous piecewise smooth signal will introduce an unneglectable error which was named as the Gibbs phenomenon. In this paper, we proposed an effective piecewise smooth signal approximation method. Firstly, a set of normal orthogonal piecewise polynomials was constructed according to the given positions of breaking points, and it has the properties of orthogonality, convergence and reproduction. Then the signal was orthogonal decomposed under this basis and the best square approximation result could be obtained using reconstruction. The numerical experiments show that our method have the higher accuracy approximation results than the other basis.

piecewise smooth signal; approximation; Gibbs phenomenon; orthogonal representation

2015-06-15,

2015-12-28；责任编辑：马兰英

国家自然科学基金(No.61170320, No.61272026)；浙江大学CAD&CG国家重点实验室开放课题(No.A1513，No.A1609)；中央高校基本科研业务费(No.JUSRP11416)

TP302.4

A

0372-2112 (2016)08-2004-05