一种可证安全的紧致无证书聚合签名方案

许 艳,黄刘生,田苗苗,仲 红,崔 杰

(1.中国科学技术大学计算机科学与技术学院,安徽合肥,230026;2.安徽大学计算机科学与技术学院,安徽合肥,230601;3.中国科学技术大学苏州研究院,江苏苏州,215123)



一种可证安全的紧致无证书聚合签名方案

许 艳1,2,黄刘生1,3,田苗苗1,3,仲 红2,崔 杰2

(1.中国科学技术大学计算机科学与技术学院,安徽合肥,230026;2.安徽大学计算机科学与技术学院,安徽合肥,230601;3.中国科学技术大学苏州研究院,江苏苏州,215123)

聚合签名能够实现批验证,特别适用于资源受限的无线网络中批量身份认证.无证书密码体制能够解决聚合签名的证书管理或私钥托管问题.本文首先对一个无证书聚合签名方案进行分析,随后提出更加安全高效的无证书聚合签名方案,方案验证时需要更少的双线性对操作.最后在随机预言模型下证明方案具有不可伪造性,其安全性等价于求解CDH(Computation Diffie-Hellman)困难问题.

无证书密码学;聚合签名;随机预言模型

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.011

1 引言

聚合签名是n个签名者分别对n个不同的消息进行签名,这n个签名可以被聚合成一个签名,验证者只需验证聚合后的签名便可以确认这些消息是否来自对应的签名者.聚合签名能够实现批验证,可用于解决资源受限的无线网络中批量身份认证问题[1,2].2003年,Boneh等[3]第一次提出聚合签名的概念,文献[4]基于陷门置换假设提出一个有序聚合签名方案,文献[5]提出基于身份的聚合签名方案.然而基于传统公钥密码体制或基于身份密码体制的聚合签名方案存在着证书管理问题或私钥托管问题.

Al-Riyami等[6]在2003年首次提出无证书公钥密码学的概念,能够解决传统公钥密码体制的证书管理问题和基于身份密码体制的私钥托管问题.在无证书密码体制中,用户私钥包括用户随机选择的秘密值和密钥生成中心(KGC)产生的部分私钥,用户公钥由秘密值生成.近年来已有不少学者对无证书签名进行研究,具有各种属性的无证书签名[7,8]相继被提出.

Gong等[9]将聚合签名与无证书密码体制相结合,首次提出无证书聚合签名方案,但是没有给出方案的安全性证明.Zhang等[10]提出一个在随机预言模型下可证安全的无证书聚合签名方案,但是聚合签名的长度随着签名人数的增加而增加.文献[11,12]中,聚合签名的长度固定,但要求每个签名者维护一个共同的状态信息.为解决上述不足,一些学者提出利用双线性对构造的无证书聚合签名方案[13～15],这些方案签名长度固定且验证高效.然而Xiong等[13]提出的无证书聚合签名方案,被He等[16]和Cheng等[17]分别指出难以抵抗恶意KGC的伪造攻击.杜红珍等[14]在随机预言模型下证明其无证书聚合签名方案的安全性可归约为CDH困难问题,然而本文研究发现杜红珍等人提出的方案(Du-Huang方案[14])难以抵抗伪造攻击,本文将对Du-Huang方案的安全性进行详细分析.随后提出一个更加安全高效的无证书聚合签名方案,方案验证时只需要使用较少的双线对操作且在随机预言模型下具有不可伪造性.此外,由于方案最终生成的聚合签名长度与聚合者的个数无关,因此是紧致的聚合签名方案.最后,与文献[14,15]提出的无证书聚合签名方案进行效率对比,我们的方案更加高效.

2 预备知识

2.1 数学困难问题

2.2 无证书聚合签名方案

定义2 无证书聚合签名方案主要参与者有KGC,签名者Pi(i=1,2,…,n),聚合者和验证者.方案由系统参数生成算法,部分私钥提取算法,用户密钥生成算法,签名算法,聚合算法,验证算法等6个多项式时间算法构成,算法具体描述请参考文献[14].

2.3 无证书聚合签名方案安全模型

无证书聚合签名方案存在两种类型的攻击者:(1)攻击者A1:不知道系统主密钥,但可以替换任意签名者的公钥；(2)攻击者A2:知道系统主密钥,但不能替换签名者的公钥.

无证书聚合签名方案安全模型可以通过挑战者C和攻击者A1,A2之间的攻击游戏来定义:

Game 1

(1)系统参数设置 挑战者C运行系统参数生成算法,得到系统参数Params和系统主密钥s.C将Params发送给攻击者A1.

(2)询问:

(a)Hash询问A1可以访问方案中所有的Hash预言机.

(b)部分私钥提取询问A1询问用户Pi的部分私钥,C运行部分私钥提取算法生成部分私钥dIDi返回给A1.

(c)秘密值询问A1询问用户Pi的秘密值,C运行用户密钥生成算法生成秘密值xi返回给A1,如果Pi的公钥已被执行过公钥替换算法,则输出⊥.

(d)公钥询问A1询问用户Pi的公钥,C运行用户密钥生成算法生成公钥pkIDi返回给A1.

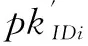
(f)无证书签名询问A1询问Pi对消息mi的签名,C输入Pi的身份IDi,公钥pkIDi生成签名σi返回给A1.

(a)至少一个Pi的身份IDi没有同时提交给公钥替换询问和部分私钥提取询问.

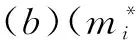
Game 2

(1)系统参数设置 与Game1类似,不同的是C将系统参数Params和系统主密钥s都发送给攻击者A2.

(2)询问 Hash询问,秘密值询问,公钥询问,无证书签名询问与Game1中对应的询问相同.

(a)至少一个Pi的身份IDi没有经过秘密值询问.

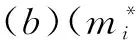
定义3 如果攻击者A1,A2在游戏Game1,Game2中获胜的概率可以忽略,那么无证书聚合签名方案在随机预言模型下,对适应性选择消息攻击是不可伪造的.

3 Du-Huang无证书聚合签名方案及安全性分析

3.1 Du-Huang无证书聚合签名方案[14]

签名者Pi(i=1,2,…,n)的身份信息为IDi,对n个消息mi进行聚合签名,方案构造如下:

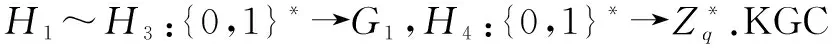
(2)部分私钥提取算法 输入Pi(i=1,2,…,n)的身份IDi,KGC验证IDi后,计算dIDi=sQi,其中Qi=H1(IDi).

(4)签名算法 输入参数params,Pi(i=1,2,…,n)的身份IDi,私钥dIDi,xi,公钥pkIDi和消息mi,不失一般性假设Pi对消息mi进行如下签名:

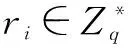
(b)计算Vi=riT+hi(dIDi+xiW),则σi=(Ui,Vi)是Pi对不同消息mi的签名.

(5)聚合 聚合人对Pi(i=1,…,n)发来的签名(mi,σi=(Ui,Vi))进行验证然后聚合.

(a)验证 计算T=H2(Ppub),W=H3(P,Ppub),hi=H4(mi,IDi,pkIDi),验证等式e(P,Vi)=e(Ui,T)e(Ppub,hiQi)e(hipkIDi,W)是否成立,若成立则接受σi否则终止算法.

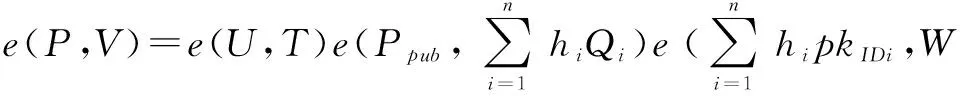
3.2 安全性分析

(1)系统参数设置 挑战算法C运行系统参数生成算法,得到系统参数params={G1,G2,e,q,P,Ppub,H1,H2,H3,H4}和系统主密钥s.将params发送给攻击者A.

(2)询问 攻击者进行签名询问,得到Pk对消息mk的聚合签名σk=(Uk,Vk).

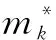
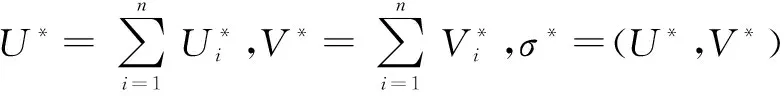
等式成立.在攻击过程中,A既没收到系统主密钥也没有执行替换公钥询问,故方案对任何类型的攻击者A1或A2都不具有不可伪造性.

此外需要注意的是,本节对Du-Huang方案[14]的攻击方法不适用于Zhou-Zhang方案[15].Du-Huang方案将明文消息映射到有限域,而Zhou-Zhang在构造签名时,将明文消息映射到加法群,而加法群中不一定存在乘法逆元,因此无法使用本节所述的攻击方法去伪造Zhou-Zhang的无证书聚合签名.

4 一个高效的无证书聚合签名方案

4.1 具体方案

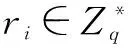
(4)签名算法 输入参数params,Pi(i=1,2,…,n)的身份IDi,私钥(di,xi)和公钥(pki,Ri),消息mi,不失一般性假设Pi对消息mi进行如下签名:

(a)计算Ti=H2(mi‖IDi‖pki‖Ri‖Ppub),Q=H3(Ppub).

(b)选择随机数wi,计算Wi=wiP.

(c)计算σi=(Tixi+di+wi)Q,将(σi,Wi)作为Pi对消息mi的签名.

(5)聚合 聚合人对Pi(i=1,…,n)发来的签名(mi,σi)进行验证然后聚合.

(a)验证 计算Ti=H2(m‖IDi‖pki‖Ri‖Ppub),Q=H3(Ppub),验证等式e(P,σi)=e(Q,Tipki+Ri+hiPpub+Wi)是否成立,若成立则接受(σi,Wi)否则终止算法.

4.2 方案分析

(1)正确性

方案的正确性证明如下.

证明 假设由签名方案得到聚合签名(σ,V),则

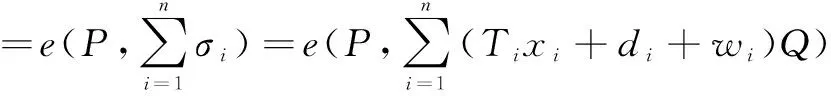
(2)抗伪造性

下面证明在随机预言模型下,本方案对攻击者A1,A2都是不可伪造的.

定理1 在随机预言模型下,如果第一类攻击者A1能够以不可忽略的概率伪造出聚合签名,则C能以不可忽略的概率解决CDH问题.

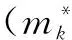
初始化C按照4.1节选择系统参数params={G1,G2,e,q,P,Ppub,H1,H2,H3},其中Ppub=P1.C将params发送给攻击者A1.A1执行如下询问,为模拟询问C维护表L1,L2,L3分别对应对H1,H2,H3的询问,表Lk1,Lk2分别对应部分私钥和秘密值的询问:

散列询问:

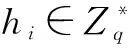
H3询问A1输入Ppub,如果L3包含(Ppub,Q)则C返回Q给A1.否则,C令Q=P2并发送给A1,同时将(Ppub,Q)写入L3.

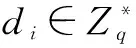
签名询问A1询问(mi,IDi)的签名.C在列表Lk1,Lk2查找IDi的部分私钥(IDi,di,Ri)和秘密值(IDi,pki,xi).随后C查找L1,L2,L3,如果①ci=1,C报错并停止执行,否则②ci=0,C返回签名σi=(Tixi+di+wi)Q.

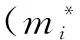
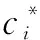
定理2 在随机预言模型下,如果第二类攻击者A2能够以不可忽略的概率伪造出聚合签名,则C能以不可忽略的概率解决CDH问题.

证明 假设存在攻击者A2满足2.3节Game2中的条件,如果A2能以不可忽略的概率ε攻破我们的方案,则挑战者C能利用A2解决CDH问题.即C已知P1=aP,P2=bP,最终能输出abP.

初始化C按照4.1节选择系统参数params={G1,G2,e,q,P,Ppub,H1,H2,H3},其中Ppub=sP.C将params和系统主密钥s发送给攻击者A2.A2执行如下询问,为模拟询问C维护表L1,L2,L3分别对应对H1,H2,H3的询问,表Lk1,Lk2分别对应部分私钥和秘密值的询问:

散列询问:

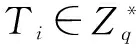
H3询问,部分私钥询问,秘密值询问,签名询问 与定理1中挑战应答相同.

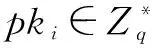
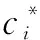
(3)效率分析

将一次双线性运算记为BP,群G1的乘法运算记为M,G1中元素的长度记为L.假设方案中有n个签名者.可以看出本文方案最终的聚合签名为σ,方案在验证时需要2次双线性运算和2n+1次加法运算,相比双线性运算和乘法运算,加法运算的时间较小可忽略不计,因此我们可将方案的验证代价记为2BP.从表1可以看出本文方案的效率要高于已有方案[14,15].同时聚合签名的长度不随签名人数的变化而变化.

表1 效率比较

5 结束语

聚合签名能够减少验证者的工作量,在资源受限的无线网络中有着重要应用.杜红珍等利用双线性对提出一个高效的无证书聚合签名方案(Du-Huang方案),并在随机预言模型下证明方案的安全性可归约CDH问题.然而本文研究发现该方案难以抵抗伪造攻击,并具体指出其安全性证明存在的不足.随后提出一个新的无证书聚合签名方案,相比Du-Huang方案,我们的方案计算量更小.最后在随机预言模型下证明了方案的安全性.

[1]Zhu H,Lin X,Lu R,et al.AEMA:An aggregated emergency message authentication scheme for enhancing the security of vehicular ad hoc networks[A].Proceedings of the 8th International Conference on Communications[C].IEEE,2008.1436-1440.

[2]Zhang C,Lu R,Lin X,et al.An efficient identity-based batch verification scheme for vehicular sensor networks[A].Proceedings of INFOCOM 2008[C].IEEE,2008.816-824.

[3]Boneh D,Gentry C,Lynn B,et al.Aggregate and verifiably encrypted signatures from bilinear maps[A].Proceedings of EUROCRYPT 2003[C].Berlin.Springer,2003.416-432.

[4]Lysyanskaya A,Micali S,Reyzin L,et al.Sequential aggregate signatures from trapdoor permutations[A].Proceedings of EUROCRYPT 2004[C].Berlin:Springer,2004.74-90.

[5]Gentry C,Ramzan Z.Identity-based aggregate signatures[A].Proceedings of Public Key Cryptography-PKC 2006[C].Berlin:Springer,2006.257-273.

[6]Al-Riyami S S,Paterson K G.Certificateless public key cryptography[A].Proceedings of ASIACRYPT 2003[C].Berlin:Springer,2003.452-473.

[7]Tian M M,Yang W,Huang L S.Cryptanalysis and improvement of a certificateless multi-proxy signature scheme[J].Fundamenta Informaticae,2014,129(4):365-375.

[8]Tian M M,Huang L S,Yang W.Practical certificateless short signature scheme[J].International Journal of Electronic Security and Digital Forensics,2014,6(3):204-218.

[9]Gong Z,Long Y,Hong X,et al.Two certificateless aggregate signatures from bilinear maps[A].Proceedings of the IEEE SNPD 2007[C].IEEE,2007.188-193.

[10]Zhang L,Zhang F T.A new certificateless aggregate signature scheme[J].Computer Communications,2009,32(6):1079-1085.

[11]Zhang L,Qin B,Wu Q,et al.Novel efficient certificateless aggregate signatures[A].Proceedings of AAECC 2009[C].Berlin:Springer,2009.235-238.

[12]Zhang L,Qin B,Wu Q,et al.Efficient many-to-one authentication with certificateless aggregate signatures[J].Computer Networks,2010,54(14):2482-2491.

[13]Xiong H,Guan Z,Chen Z,et al.An efficient certificateless aggregate signature with constant pairing computations[J].Information Sciences,2013,219:225-235.

[14]杜红珍,黄梅娟,温巧燕.高效的可证明安全的无证书聚合签名方案[J].电子学报,2013,41(1):72-76.

DU Hong-zhen,HUANG Mei-juan,WEN Qiao-yan.Efficient and Provably-secure certificateless aggregate signature scheme[J].Acta Electronica Sinica,2013,41(1):72-76.(in Chinese)

[15]Zhou M,Zhang M,Wang C,et al.CCLAS:A practical and compact certificateless aggregate signature with share extraction[J].International Journal of Network Security,2014,16(2):157-164.

[16]He D B,Tian M M,Chen J H.Insecurity of an efficient certificateless aggregate signature with constant pairing computations[J].Information Sciences,2014,268:458-462.

[17]Cheng L,Wen Q Y,Jin Z,et al.Cryptanalysis and improvement of a certificateless aggregate signature scheme[J].Information Sciences,2015,295:337-346.

许 艳 女，1982年生，现为中国科学技术大学计算机科学与技术学院博士生，研究方向为信息安全和密码学.

E-mail:xuyan@ahu.edu.cn

黄刘生 男，1957年生，现为中国科学技术大学计算机科学与技术学院教授，博士生导师，主要研究方向为无线传感网络、信息安全和分布式计算.

A Provably Secure and Compact Certificateless Aggregate Signature Scheme

XU Yan1,2,HUANG Liu-sheng1,3,TIAN Miao-miao1,3,ZHONG Hong2,CUI Jie2

(1.SchoolofComputerScienceandTechnology,UniversityofScienceandTechnologyofChina,Hefei,Anhui230026,China;2.SchoolofComputerScienceandTechnology,AnhuiUniversity,Hefei,Anhui230601,China;3.SuzhouInstituteforAdvancedStudy,UniversityofScienceandTechnologyofChina,Suzhou,Jiangsu215123,China)

Aggregate signature schemes are particularly useful for authentication in resource-constrained wireless networks for realizing batch verification.Certificateless cryptosystems can resolve the certificate management problem or key escrow problem in aggregate signature schemes.This paper firstly analyzed a certificatelss aggregate signature(CLAS) scheme.Then,a more efficient CLAS scheme that requires less bilinear paring operations was provided.The security analysis showed that this scheme can resist the forgery attack under the random oracle model,the security was equal to resolve CDH problem.

certificateless cryptography;aggregate signature;random oracle model

2015-01-15;

2015-09-14；责任编辑：马兰英

国家电网基础前瞻性项目(No.XXN51201304253);国家自然科学基金(No.61572001，No.61502443);中国博士后科学基金(No.2015M570545);安徽省自然科学基金(No.201508085QF132)；安徽大学信息保障技术协同创新中心开放课题(No.ADXXBZ2014-9)

TP309

A

0372-2112 (2016)08-1845-06