基于方向性遗传-粒子群混合算法的有源配电网无功优化

王树洪 邵振国

（福州大学电气工程与自动化学院，福州 350116）

基于方向性遗传-粒子群混合算法的有源配电网无功优化

王树洪 邵振国

（福州大学电气工程与自动化学院，福州 350116）

以网损和越限电压之和最小为目标，改进电压越限罚系数，建立了有源配网无功优化的数学模型，提出了一种方向性遗传—粒子群混合算法。在优化过程中交替进行遗传和粒子群进化，用转置雅可比矩阵法求解配电网中无功调节点的网损微增率，指导GA变异，加强搜索方向；用记忆算子使GA的选择算子不破坏PSO的记忆功能，并在每代的记忆操作后更新个体速度以保证算法的收敛速度。仿真结果表明，该方法降低了GA搜索的随机性，并弥补了PSO容易陷入局部最优的不足。

有源配电网；无功优化；网损微增率；遗传算法；粒子群算法；方向性

无功优化借助调节发电机机端电压、有载调压变压器变比或改变无功补偿装置出力等措施来调整无功潮流，在一定的约束条件下优化系统性能指标。将分布式发电（Distributed Generation，DG）与传统无功电压调整装置相配合，使配电网运行得更加经济、可靠是当前的研究热点。经典无功优化应用线性规划、二次规划、非线性规划、内点法等，要求目标函数和约束条件可导，容易陷入局部最优。人工智能类算法包括模拟退火法［1］、禁忌搜索法［2］、蚁群算法［3］、粒子群算法［4］、遗传算法［5-6］等，不需要目标空间的导数信息，对函数性态的依赖性较小。其中遗传算法和粒子群算法在解决多变量、非线性、不连续、多约束问题时显示出良好的性能，在无功优化中得到较多运用。

每一种优化算法都有各自的优点和不足，单单一种算法有时达不到理想的效果。文献［7］以交直流系统为优化对象，在进化中采用自适应概率选择遗传算法或粒子群算法进行优化。文献［8］在不考虑离散约束的情况下先用内点法得到初始解，再将无功优化问题分解为离散优化和连续优化两个子问题，采用遗传算法和内点法交替求解。

启发式的随机搜索通过随机地遍顾全局来避免陷入局部最优，但也存在耗时长、局部搜索能力不强等问题。因而需要采取措施压缩人工智能算法的搜索空间，增强搜索的方向性。文献［9］利用两个个体的差矢量确定变异方向，强化算法的搜索方向，提出了基于进化方向的定向变异遗传算法。文献［10］在粒子群算法中采用外推技巧引导粒子位置的更新。文献［11］采用Alopex方法获取搜索方向，降低搜索的随机性。

本文提出一种方向性遗传-粒子群混合无功优化算法。在优化过程中交替进行GA和PSO，用转置雅可比矩阵法计算调节点有功网损对注入无功的网损微增率，指导变异操作。采用记忆算子确保GA的选择算子不破坏PSO的记忆功能，并在每代的记忆操作之后更新个体的速度以保证算法的收敛速度。该方法降低了GA搜索的随机性，并弥补了PSO容易陷入局部最优的不足。通过IEEE 33节点配电网算例仿真，验证了该方法的优异性。

1 有源配电网无功优化数学模型

1.1 等式约束

电网等式约束如式（1）所示。Pi、Qi为节点 i的注入有功、无功；Ui、Uj为节点i、j的电压幅值；Gij、Bij分别是节点导纳矩阵元素的实部和虚部，θij为节点i、j之间的电压相角差。

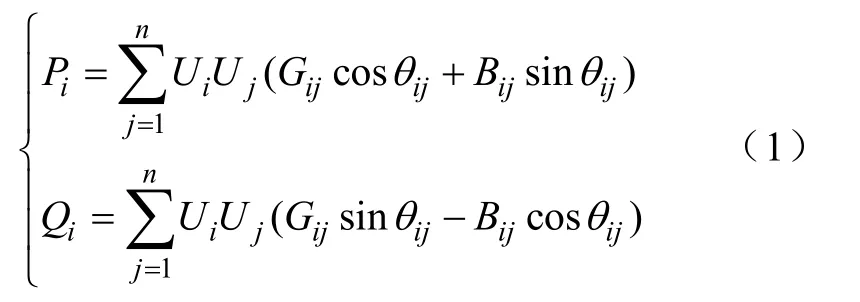
1.2 不等式约束

本文无功优化的控制变量为可调变压器分接头档位T、电容器组投切组数C、DG无功出力QDG、SVC的无功出力QSVC。状态变量为节点电压U。

控制变量的不等式约束如式（2）所示。

状态变量的不等式约束如式（3）所示。

式中，Ti为第 i个可调变压器的档位，Timin、Timax为对应档位的最小值和最大值；Ci是第 i个可投切电容器组的投切组数，Cimax为最大投切组数；QiDG为第i个可参与调节的DG无功出力，QiDGmin、QiDGmax为无功出力下限值和上限值；QiSVC为第i个SVC的无功出力，QiSVCmin、QiSVCmax分别为其下限和上限。Ul、Uu分别是节点电压下限和上限。

1.3 目标函数

以配电网的总有功网损最小为目标，并把状态变量越界量乘以一个罚系数加到目标函数中以体现状态变量的约束，如式（4）所示。其中，PL为配电网的总有功网损，λ 为越限电压罚系数，n为网络节点数。

2 网损微增率的计算和特殊节点的处理

2.1 网损微增率的计算

网损微增率是总网损对节点注入有功功率或无功功率的偏微分值，代表着节点功率变化对网损的影响程度。根据网损微增率选择控制量及大小方向，可以使系统网损更快地往小的方向变化。

在网损微增率的计算方法中，B系数法［12］、阻抗矩阵法［13］、导纳矩阵法［14］有不同程度的简化和近似，本文选用转置雅可比矩阵法，计算公式如式（5）所示［15］。

2.2 潮流计算中特殊节点的处理

有源配电网中由于分布式电源的接入而产生了一些新的比较特殊的节点，如P-I节点［16］和P-Q（V）节点［17-18］，这在潮流计算中需要特殊处理。设在系统节点j和节点i分别接入P-I节点和P-Q（V）节点。本文在牛顿-拉夫逊法的基础上进行处理。

1）P-I节点:光伏发电系统通过电流控制逆变器接入电网时，将被处理为有功输出P和注入电网电流I恒定的P-I节点。

首先，初始化节点电压和节点注入无功功率

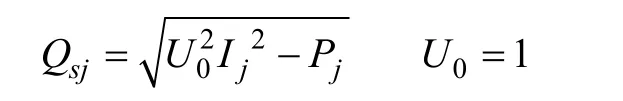
求出新的电压之后，根据电压更新节点注入无功

然后再根据注入无功求出新的节点电压，根据电压更新节点注入无功。以此类推，一次次迭代，便可得到符合条件的解。

2）P-Q（V）节点:异步风力发电机处理为P-Q（V）节点，有功出力知道，无功出力和电压关系知道。

根据异步风力发电机特性，其出力和节点电压有如下关系，其中X为节点电压相角和幅值组成的向量，xδ为风机定子漏抗和转子漏抗之和，xm为风机的激磁电抗

联合潮流方程和风电出力特性有

则将原来潮流方程中Qsi=C（X）替换为0=C（X）－f（X），这样雅可比矩阵相应元素由 U（∂C（X）/∂X）变为U（∂C（X）/∂X－∂f（X）/∂X），最终结果是雅可比矩阵

中L的第i行，第i列元素加上

3 方向性遗传-粒子群交替优化

本文的遗传算法和粒子群算法共用编码方式，编码为浮点数和整数混合编码，个体X有6个控制变量，分别为有载调压变压器档位T1、电容器组投切组数C1和C2、双馈式风力发电机DFWP无功出力QDFWP、静态无功补偿器SVC的无功出力QSVC1和QSVC2。即X=［T1，C1，C2，QDFWP，QSVC1，QSVC2］。其中T1、C1、C2为离散变量，采用整数编码；QDFWP、QSVC1、QSVC2为连续变量，采用浮点数编码。

在每一代的进化中，先后采用遗传算法和粒子群算法更新群体。粒子群算法记忆优化过程中的个体速度和个体极值，以供后续的更新过程使用。在遗传算法中，加入记忆算子来确保粒子群算法的记忆功能不被破坏，并加入个体速度更新操作以加快算法收敛。

在以下操作中，r、r1、r2表示0到1之间的随机数；R（）是四舍五入取整函数；t为当前进化代数，T为最大进化代数。在论述到个体变量 X、速度变量V及适应度f时，用下标i表示变量属于个体i，用下标j表示个体的第j维变量，下标pbest表示变量的个体极值，下标gbest表示变量的全局极值，上标′表示更新后的变量。

在遗传操作和粒子群操作的个体速度更新中，限制-Vjmax≤Vij≤Vjmax，其中Vjmax为预先设定的个体第j维的最大飞行速度，取为个体第j维控制变量搜索范围的30%。一旦Vij越限则取为限值-Vjmax或Vjmax。

3.1 适应度函数

适应度函数为目标函数的倒数，如式（6）所示，其中改进的电压越限罚系数λ 如式（7）计算。

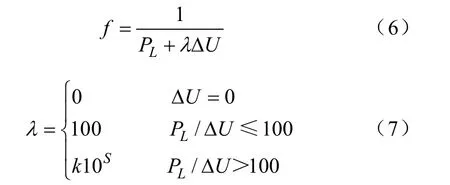
式中，S=［log10（PL/ΔU）］，k=1/3，［X］表示取小于等于X的最大整数。

3.2 遗传算法操作

本文遗传算子的执行顺序依次为选择、记忆操作、速度更新、变异、交叉。

1）选择

采用锦标赛选择策略，从种群中随机抽取5个个体，选择其中适应度最好的个体作为子代。每次抽取后放回个体，重复抽取直至达到所需种群规模为止。

2）记忆操作

采用记忆算子使得每个被选择的个体都继承自己的个体极值和速度。如式（8）和图1所示。

式中，s（i）为选择操作之后的个体i在选择操作之前的序号。

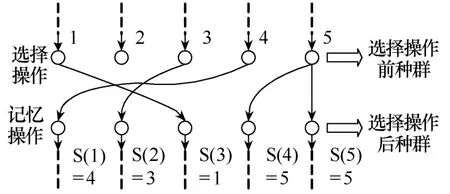
图1 选择和记忆过程

3）速度更新

为了加快收敛速度，在遗传操作部分加入如式（9）所示的个体速度更新操作。

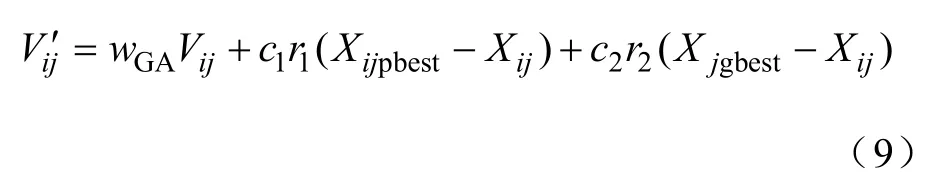
式中，加速因子c1=c2=2，惯性因子取wGA=0.3。

4）变异

对于个体i的各维变量，按变异概率进行变异，并采用网损微增率指导变异过程。

若Xij为变压器分接头档位变量，则按式（10）进行完全的随机变异。

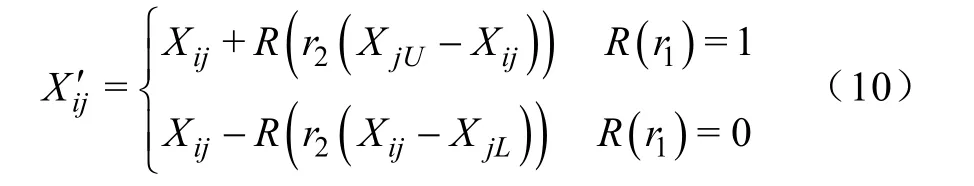
若Xij是无功补偿离散变量，则按式（11）进行方向性变异。若 Xij是无功补偿连续变量，则按式（12）进行方向性变异。

式中，N（j）为第 j个控制变量对应的配电网节点序号，QN（j）为该节点注入的无功功率，∂PL/∂QN（j）为对应的有功网损对注入无功的网损微增率。自适应步长s=smax-（smax-smin）t/T，smax=1，smin=0.2。XjU表示第j个控制变量的上限，XjL表示第j个控制变量的下限。

5）交叉

将种群中相邻的个体配对，在满足交叉概率时对每对个体中的各维控制变量进行均匀交叉操作。其中连续变量按式（13）操作，离散变量按式（14）操作。

3.3 粒子群算法操作

按式（15）更新速度，按式（16）更新连续变量的位置，按式（17）更新离散变量的位置。

式中，采用自适应下降的惯性权重wPSO，计算式为wPSO=wmax-（wmax-wmin）t/T，wmax=0.9，wmin=0.1。

3.4 精英保留策略

如果进化后的全局极值更优，则保留新的全局极值及其对应的适应度、潮流参数和速度。同时在粒子群操作过后、下一代遗传选择操作之前，用全局极值及其对应的适应度、潮流参数和速度替换种群中最差的个体对应量。

3.5 算法流程

方向性遗传-粒子群混合算法的具体流程如下。

1）输入网络参数和算法参数，随机生成初始群体和初始速度，计算适应度和潮流参数。

2）以每个个体本身为个体极值，以最优个体为全局极值，保存全局极值及其对应的适应度、潮流参数和速度，设置t=1。

3）用锦标赛策略选择较优个体组成新的种群；根据式（8）进行记忆操作。

4）根据式（9）更新个体速度。

5）由式（5）和潮流参数计算网损微增率，并根据式（10）—式（12）用网损微增率指导变异操作。

6）根据式（13）、式（14）进行均匀交叉操作。

7）计算适应度和潮流，更新个体极值和全局极值，保存全局极值及其对应的适应度、潮流和速度。

8）根据式（15）—式（17）更新个体速度和位置。

9）再次计算适应度和潮流，更新个体极值和全局极值，保存全局极值及其对应的适应度、潮流和速度，用全局极值及其对应的适应度、潮流和速度替换群体中最差个体的相应量。

10）如果t＜T，t=t+1，返回上述步骤3）；否则输出当前最优解，算法结束。

4 算例分析

4.1 仿真条件

用IEEE 33节点系统验证所提算法的可行性，接线图如图 2所示，参数见文献［16］和附录。系统节点电压标幺值上下限分别为1.04和0.96。节点21接入光伏系统，看作P-I节点；节点32通过变压器T2（分接头不可调）接入异步风力发电机，看作P-Q（V）节点。算法种群size=30，最大进化代数T=40，交叉概率Pc=0.6，变异概率Pm=0.2。

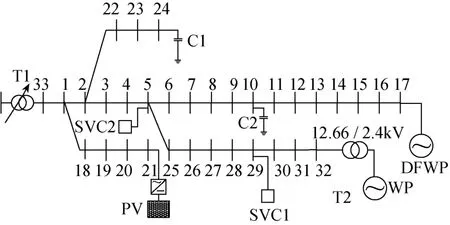
图2 IEEE 33节点系统

4.2 仿真结果

优化前后设备的动作情况见表1。其中加“*”的为不参与无功调节的非控制变量。

表1 优化前后设备的动作情况

由表1可以看出，双馈风机DFWP优化后的无功补偿量很小，节点 17的电压不超过上限；节点29的静止无功补偿器 SVC1优化后用最大容量进行补偿，使节点27—32的电压不低于下限。

优化前后配电网的节点电压如图3所示。从图3可以看出，优化前有一部分节点电压越限，经过本文方法优化之后，配电网没有出现电压越限。

图3 优化前后配电网节点电压

将本文方法的优化结果和未优化结果、常规改进遗传算法的优化结果和标准粒子群算法的优化结果进行比较。常规改进遗传算法的编码方式、种群规模、交叉概率、变异概率、选择算子、交叉算子、适应度函数都和本文算法一致，也采用精英保留策略，不同的只是不采用网损微增率指导变异操作。标准粒子群算法惯性因子采用自适应下降惯性权重，种群规模、适应度函数和本文方法一样。将本文算法、常规改进遗传算法和标准粒子群算法分别进行20次的优化计算，各次优化的结果如图4、图5所示。并分别取这三种算法20次优化的网损、计算时间的平均值，列于表2之中。这里需要说明的是，本文方法是一种混合算法，一代进化中包含遗传操作和粒子群操作，所以一代进化相当于于常规算法的两代进化，所以混合算法的40代和常规算法的80代是等价的。

图4 常规改进遗传算法和本文方法各次化结果

图5 标准粒子群算法和本文方法优化结果

从图4可以看出，常规改进遗传算法的网损值除了有几次和本文方法接近，大部分都比本文方法得到的网损值大；而且用常规改进遗传算法局部搜索效果差，容易陷入局部最优。

从图5可以看出，标准粒子群算法局部搜索效果比常规改进遗传算法好，但也会陷入局部最优值。从图 4、图 5可以看出本文方法降低了遗传算法的搜索随机性，并弥补了粒子群算法容易陷入局部最优的不足，有很好的全局和局部搜索能力。

由表2可以看出，优化前的网损为196.34kW，常规改进遗传算法、标准粒子群算法和本文方法都能够降低网损。常规改进遗传算法得到的平均网损为 126.85kW，标准粒子群算法得到的平均网损为126.92kW，本文方法得到的平均网损为126.46kW，证明了本文方法能够搜索到更优的结果。从计算时间上看，本文方法的平均时间比常规改进遗传算法的平均时间多 1.3s，比标准粒子群算法多 0.1s，耗时只是略微增加，计算效率基本得到保持。总的来说，本文方法在基本保持计算效率的基础上，使得网损得到明显的降低，说明方法是可行的。

表2 网损优化结果

5 结论

本文提出了一种基于方向性遗传-粒子群混合的无功优化算法。用转置雅可比矩阵法计算调节点的有功网损对注入无功的网损微增率，指导变异操作；在优化过程中交替进行GA和PSO，采用记忆算子确保GA的选择算子不破坏PSO的记忆功能，并在每代的记忆操作之后更新粒子的速度以保证算法的收敛速度。该方法降低了GA搜索的随机性，并弥补了PSO容易陷入局部最优的不足，寻优过程更有方向性。通过在IEEE 33节点系统进行仿真验算，和常规改进的遗传算法、标准粒子群算法进行比较，验证了本文方法的有效性。

将两种甚至多种启发式的随机算法有机结合，扬长避短，可以使算法发挥出更好的性能。利用优化过程中的网络潮流信息指导启发式的随机算法，可以增强其无功优化搜索的方向性和目的性，降低其搜索的随机性和盲目性。但如何根据算法的特点选择适合结合的算法，如何设计算法结合的方式；利用哪些网络潮流信息，如何充分地利用所选取的网络潮流信息——这些都是有待进一步研究的问题和方向。

［1］贾德香，唐国庆，韩净.基于改进模拟退火算法的电网无功优化［J］.继电器，2004，32（4）：32-35.

［2］杨银国，张伏生，贺春光，等.配电网无功电压优化控制求解的一种新方法［J］.电力系统自动化，2005，29（9）：45-49.

［3］周鑫，诸弘安，马爱军.基于多种群蚁群算法的多目标动态无功优化［J］.电网技术，2012，36（7）：231-236.

［4］赵晶晶，符杨，李东东.考虑双馈电机风电场无功调节能力的配电网无功优化［J］.电力系统自动化，2011，35（11）：33-38.

［5］NIKNAM T，RANJBAR A M，SHIRANI A R.Impact of distributed generation on volt/Var control in distribution networks［C］.2003.

［6］赵昆，耿光飞.基于改进遗传算法的配电网无功优化［J］.电力系统保护与控制，2011，39（5）：57-62，68.

［7］彭磊，张建平，吴耀武，等.基于 GA、PSO结合算法的交直流系统无功优化［J］.高电压技术，2006，32（4）：78-81.

［8］刘方，颜伟，David CY.基于遗传算法和内点法的无功优化混合策略［J］.中国电机工程学报，2005，25（15）：67-72.

［9］耿光飞，杨仁刚.基于定向变异遗传算法的地区电网无功功率优化［J］.电网技术，2004，28（10）：42-44，54.

［10］刘丽军，蔡金锭.基于自适应强引导粒子群算法的电力系统无功优化［J］.电工电能新技术，2012，31（4）：24-28，38.

［11］黄志刚，李林川，杨理，等.电力市场环境下的无功优化模型及其求解方法［J］.中国电机工程学报，2003，23（12）：79-83.

［12］ERWIN S R，FALLON S A，GIBSON C A.On-line calculation of incremental transmission losses in an electric power system［C］.Knoxville，TN：1988.

［13］王主丁，邢颢华，冯祈善，等.网损微增率计算方法的研究——阻抗矩阵法网损微增率计算公式的再认识［J］.电力系统及其自动化学报，1994，6（4）：13-22.

［14］陈恳，李小锐，徐敏.网损微增率新解法与转置雅可比矩阵法用于有功优化计算的比较［J］.中国电机工程学报，2000，20（7）：35-37，40.

［15］陈珩.电力系统稳态分析［M］.北京：水利电力出版社，1985.

［16］王守相，黄丽娟，王成山，等.分布式发电系统的不平衡三相潮流计算［J］.电力自动化设备，2007，27（8）：11-15.

［17］陈海焱，陈金富，段献忠.含分布式电源的配电网潮流计算［J］.电力系统自动化，2006，30（1）：35-40.［18］王守相，江兴月，王成山.含风力发电机组的配电网潮流计算［J］.电网技术，2006，30（21）：42-45，61.

［19］Baran M E，Wu F F.Network reconfiguration in distribution systems for loss reduction and load balancing［J］.Power Engineering Review，IEEE，1989，9（4）：101-102.

附 录

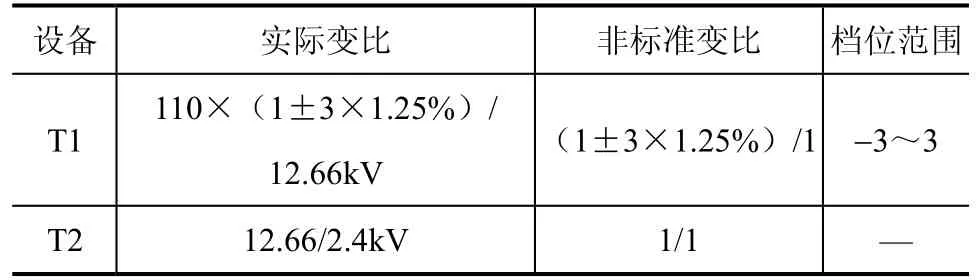
表1 变压器参数

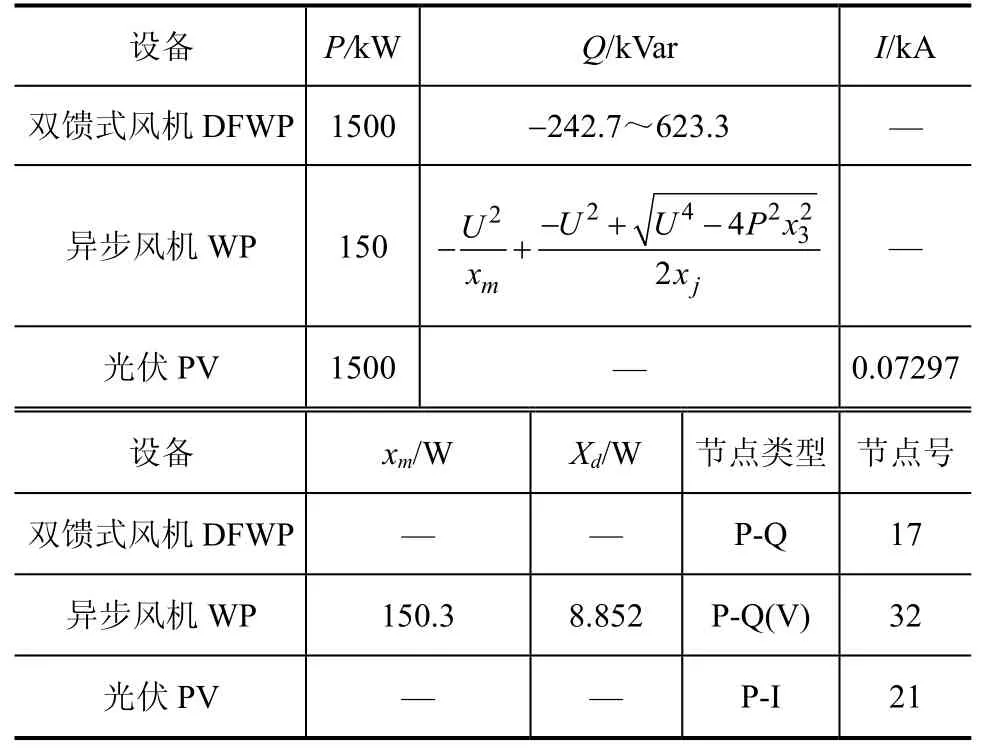
表2 分布式电源参数

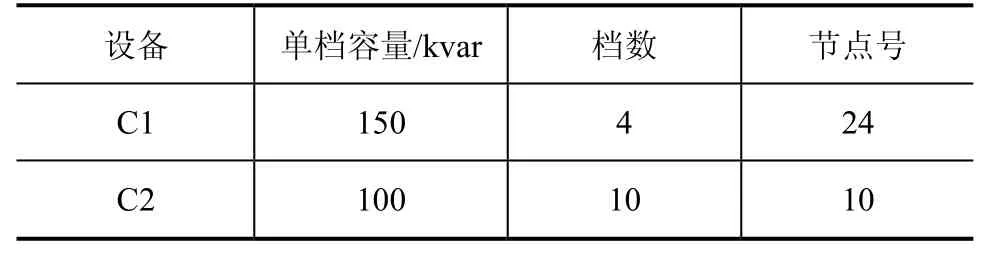
表3 电容器组参数

表4 静态无功补偿器参数

备注:上表中，xm、xδ为异步风力发电机内部阻抗参数，U为异步风力发电机节点电压幅值。

Reactive Power Optimization of Distribution Networks with DG based on a Directional GA-PSO Hybrid Algorithm

Wang Shuhong Shao Zhenguo
（College of Electrical Engineering and Automation，Fuzhou University，Fuzhou 350116）

A directional reactive power optimization method for distribution networks with distributed generation that combine genetic algorithm（GA）and particle swarm optimization（PSO）is proposed in this paper.It first builds the mathematical model aiming to the minimum sum of active power loss with the over-limit voltage，besides，improves the penalty coefficient of the over-limit voltage.Secondly it runs GA and PSO alternately.In the process，the mutation operation is guided by the incremental transmission losses of control variable computed by transposed Jacobian matrix method.In addition，memory operator and speed update operator are added to GA to protect the memory function of PSO and enhance convergence speed respectively.The simulation result shows that the method could reduce the randomicity of GA and reduce the possibility of trap in local optimum in PSO.

active distribution networks；reactive power optimization；incremental transmission losses； genetic algorithm； particle swarm optimization； directional

王树洪（1989-），男，福州大学在读硕士研究生，主要研究方向为电力系统无功优化。