基于变参MQ拟插值格式求解Burgers方程
2016-11-17李焱淼王园园张继红王瑞林
李焱淼,王园园,张继红,王瑞林
(大连交通大学 理学院,辽宁 大连 116028)*
基于变参MQ拟插值格式求解Burgers方程
李焱淼,王园园,张继红,王瑞林
(大连交通大学 理学院,辽宁 大连 116028)*
提出了一种单变量变参数的MQ拟插值算法,并用它来求解Burgers方程.在拟插值过程中,采用可变参数替换原有的常参数,避免了常参数选取困难这一问题,并通过数值算例验证了方法的有效性.通过与原有方法的对比,提出的新方法精度要更高一些,且参数的选取要容易一些.
MQ拟插值;Burgers方程;变参数;径向基函数
0 引言
Multiquadrics(MQ)是由R.L.Hardy[1]于1968年提出来的一种径向基函数,Franke在其文献[2]中指出:就精度,稳定性,有效性,内存需要和易于实现这些方面而言,MQ在所有的29类散乱数据插值格式中是首屈一指的.1994年,Wu和Schaback[3]构造了基于MQ径向基函数的拟插值格式LD,该方法操作简单,不需要解任何线性方程组,避免了节点较多时,插值方法易产生病态的问题,随后LD被应用到各个领域.但是由于该格式存在一个自由参数,它的选取直接影响计算精度,所以有关参数的研究,得到了广泛的关注.
本文首先介绍了MQ拟插值格式LD,然后给出变参MQ拟插值格式,并将其应用于Burgers方程.通过将常参数改为变参数,避开了常参数的最优选取问题.数值实验验证了这种方法的有效性.
1 MQ拟插值
Wu和Schaback[3]在Beatson和Powell[4]的基础上,提出了有限区间[x0,xN]上函数f(x)的单变量MQ拟插值逼近格式LD.
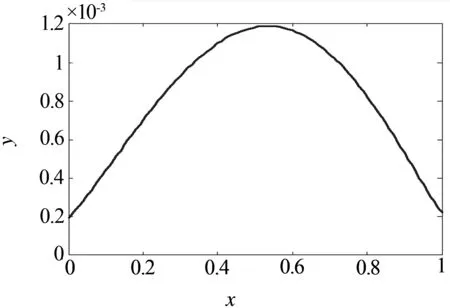
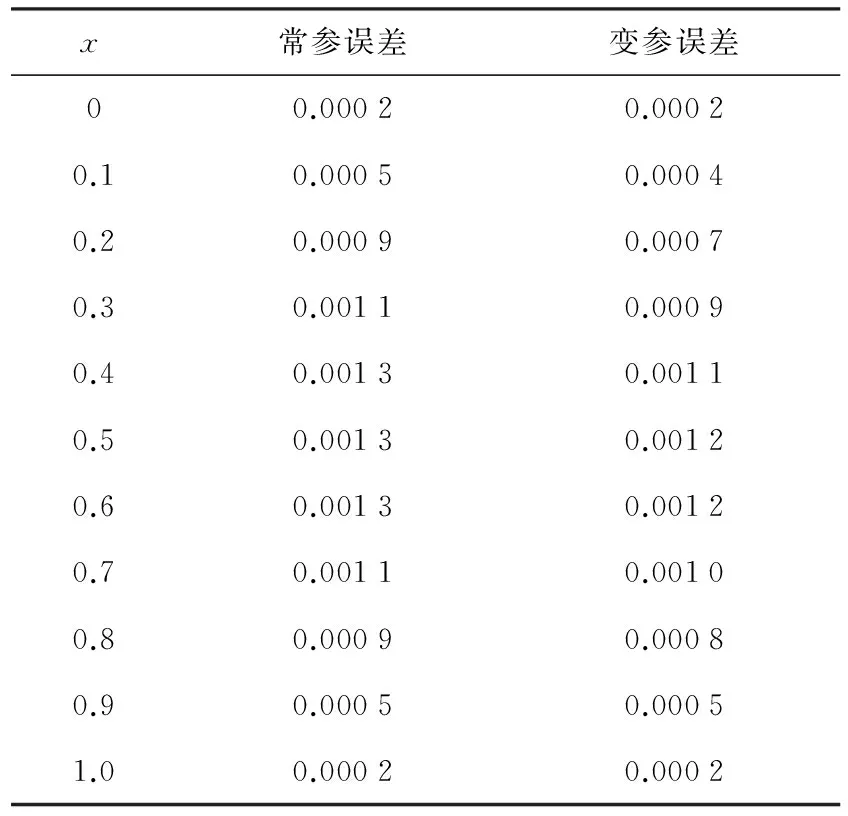
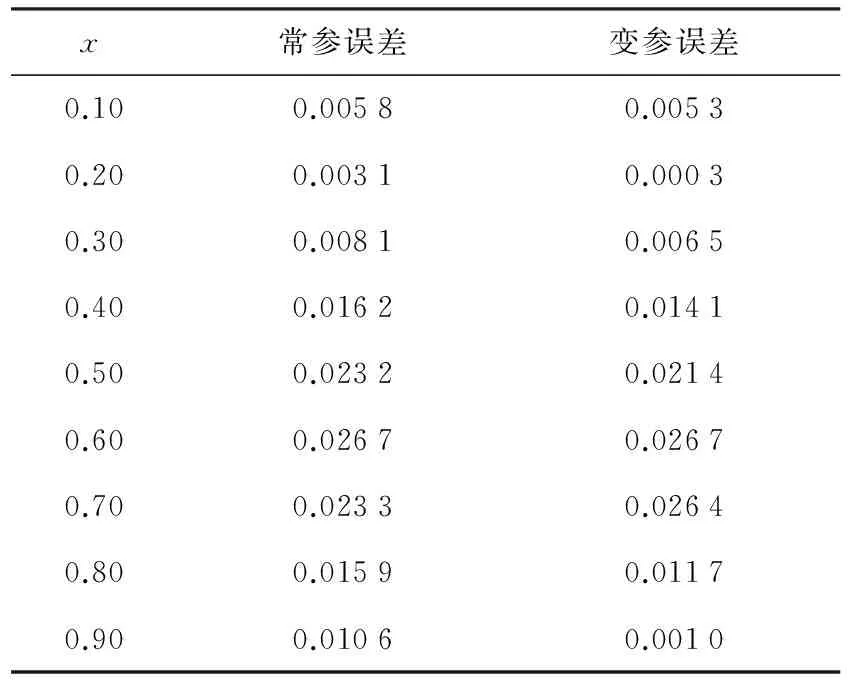
对给定数据{xj,fj},fj=f(xj), j=0,1,…,n,x0 其中, 其中,c为常数,称为形状参数. 定理1[5-6]拟插值格式LDf具有保线性、保单调性且可以改写成如下形式: 此外,在[x0,xN]上,LDf的一阶导数和二阶导数如下: 常参MQ拟插值算法中参数c的选取非常关键,c选取的好,那么结果就非常好,如果C选取的不好,那么拟插值的结果误差就很大.为了避开常参数选取的困难,本文提出了变参MQ拟插值这种算法.也就是说,本文不再使用常参数,而是采用可变的形状参数,就是在每一步的计算中参数的值是不同的. 本文采用文献[7-8]中给出的可变形状参数: 下面考虑函数逼近情况,分别用常参及变参MQ拟插值格式近似函数u(x)=sinπx,0≤x≤1,当取常参数c=0.0072,N=100时其计算结果误差如图1所示. 图1 常参MQ算法近似函数绝对误差 当N=100,cmin=0.006,cmax=0.008时,采用变参拟插值格式结果见图2. 图2 变参MQ算法求得的函数的结果 本文比较两种计算方法的计算结果与真实值的误差见表1. 表1 两种方法绝对误差比较 x常参误差变参误差00.00020.00020.10.00050.00040.20.00090.00070.30.00110.00090.40.00130.00110.50.00130.00120.60.00130.00120.70.00110.00100.80.00090.00080.90.00050.00051.00.00020.0002 由此本文可以看出这个方法是可行的,参数的选取相对要简单,变参只需要给出一个参数范围,而不会像常参数,要给出一个常数,这个最优常数是很难选取的.同时,可以看出变参的计算效果还要更好一些. 将变参MQ拟插值格式应用到Burgers方程的求解中. 考虑初边值问题: 初始条件u(x,0)=g(x),边界条件u(x0,t)=a(t),u(xN,t)=b(t),雷诺数R=10. 本文用向前差分格式将时间进行离散化: 然后用变参MQ拟插值格式来逼近函数及其导数. 其中 当τ=0.001,h=0.01时,分别用常参和变参MQ拟插值格式求解Burgers方程,其计算结果分别如图3,图4所示,其中常参数c=0.007 2,变参数cmin=0.006,cmax=0.008. 图3 常参MQ算法求解Burgers方程结果 图4 变参MQ算法求解Burgers方程结果 本文比较两种算法在时间t=1时与真实值的计算误差,其结果见表2. 表2 在t=1的绝对误差比较 由此,本文可以看出变参MQ拟插值格式求解Burgers方程是可行的,并且它的精确度比常参数MQ算法还要高,便于实现,且避开了最优常参数选取的问题. 本文通过采用可变形状参数,给出了变参MQ拟插值算法,并且将它应用到了Burgers方程的数值求解中.数值算例验证了本文所提算法的有效性,算法简单,易于实现,且避开了插值问题可能出现的病态现象以及最优常参数很难选取的问题.将参数选取问题由点转换为一个区间范围的问题.但事实上,变参数的选取仍然还有进一步研究的空间,这也是本文未来的研究方向. [1]HARDY R L. Theory and applications of the multiquadric biharmonic method, 20 years of discovery 1968-1988[J]. Computers and Mathematics with Applications,1990, 19(8/9):163-208. [2]FRANKE R. Scattered data interpolation:test of some methods[J].Math. Comput, 1982,38:181-200. [3]WU Z M, SCHABACK R. Shape preserving properties and convergence of univariate multiquadric quasi-interpolation[J]. ACTA Math. Appl Sinica, 1994,10(4): 441-446. [4]BEATSON R K, POWELL M JD. Univariate multiquadric approximation to scattered data[J]. Constr.Approx,1992,8:275-288. [5]陈荣华,吴宗敏,韩旭里. 一种新的Multiquadric拟插值[J]. 工程图学学报,2010(3):117-121. [6]CHEN RONG HUA,WU ZONG MIN.Applying multiquadric quasi-interpolation to solve Burgers′equation[J]. Applied Mathematics and Computation, 2006,172: 472-484. [7]KANSA E J, CARLSON R. Improved accuracy of multiquadric interpolation using variable shape parameters[J]. Computers and Mathematics with Applications, 1992,24: 99-120. [8]SCOTT A. SARRA, DEREK STURGILL.A random variable shape parameter strategy for radial basis function approximation methods[J]. Engineering Analysis with Boundary Elements, 2009,33: 1239-1245. An MQ Quasi-Interpolation Method with a Variable Shape Parameter for Solving Burgers Equation LI Yanmiao ,WANG Yuanyuan,ZHANG Jihong,WANG Ruilin (School of Mathematics and Physis, Dalian Jiaotong University, Dalian 116028, China) An MQ quasi-interpolation algorithm with a variable shape parameter is proposed, and it is used to solve the Burgers equation. To avoid the selection of the optimal parameter, the variable parameter is used to replace the original one. Numerical examples verify that the proposed method is more accurate and easier. MQ quasi-interpolation; Burgers equation; variable parameter; radial basis function 1673-9590(2016)04-0114-04 2015-12-10 辽宁省教育厅科学研究计划资助项目(L2012167) 李焱淼(1978-),女,副教授,硕士,主要从事数值代数方面的研究E-mail:lilaclym@sina.com. A2 变参MQ拟插值格式

3 变参MQ拟插值求解Burgers方程
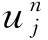
4 数值算例
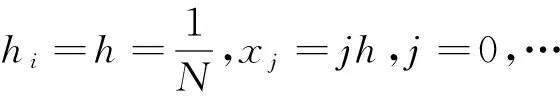


5 结论
