基于Rough Sets理论的保障房项目后评价指标体系优化

王 波

基于Rough Sets理论的保障房项目后评价指标体系优化

王 波

（重庆第二师范学院 旅游与服务管理系，重庆 400040）

保障性住房项目是社会保障体系的重要组成部分，关乎民生与社会和谐。首先对保障房项目后评价的主要内容和特点进行分析，采用改进型德尔菲法与HHM法，从项目目标、执行过程、项目影响、项目效益、项目可持续性等五个维度对保障房项目的后评价指标进行识别与筛选。而后通过基于知识粒度与属性重要度的Rough Sets（粗糙集）理论对所有指标的重要度、指标权重、偏离程度进行计算，剔除与约简了偏离程度较大的冗余指标，建立起了更加科学合理的符合保障房项目固有特点的后评价指标体系，以期为以后的保障房项目后评价管理以及全寿命周期管理提供研究基础。

保障房项目； 后评价； 指标体系优化； 知识粒度； Rough Sets理论

持续改善城市低收入群体的居住条件，是重要的社会民生问题。持续推进和优化保障性安居项目建设，对改善民生、促进社会和谐与稳定具有重要意义。随着社会经济高速发展和城市低收入群体生活需求的不断提高，在能满足基本居住条件的基础上，低收入群体对保障性住房的功能、质量、配套设施、交通方便性、物业综合服务等方面也有了越来越高的要求［1］，这使得政府对保障房项目决策水平与开发商项目建设管理水平提出了新的挑战。

建立和逐步完善保障房项目后评价指标体系一直是保障房项目相关领域研究的重点［2，3］。目前关于保障房项目后评价指标体系的研究，从国家到省、市政府层面还未设立相关的保障房项目后评价标准与强制性规定［4］。相关后评价指标体系理论从90年代中后期开始逐步发展，Retzlai、Rebecca等认为构建一套完整合理的保障房项目后评价指标体系有助于检验保障项目的发展是否符合可持续发展的目标；国内学者在总结美国LEED评价体系与日本GB Tool等后评价指标体系之后，对保障房项目后评价中的社会评价进行了进一步研究，增加了社会评价与人文评价的指标内容，为实际工作提供指导；李玲以保障性住房的质量水平为切入点，从组织架构、管理方法、运作阶段和项目成果四个维度来评价建成后保障性住房的质量体系；王立里、蒋泽熙等人从利益相关方的角度出发提出保障房项目后评价指标应包含财务、项目建设过程、管理效率、内部协调管理、居住需求、国民经济、投资需求、社会影响效益、环境影响效益、周边居民影响等后评价指标。虽然目前我国对住宅地与商业地产领域的后评价体系研究取得了一定进展，但国内对保障房项目这一具有社会特殊性质的建设项目涉及到的研究基础与后评价系统甚少，还未对保障房项目的后评价指标体系进行过系统研究。因此，建立一套比较合理、精简、科学的保障房项目后评价指标体系，对总结决策阶段和建设阶段的经验与教训，为后期保障项目群决策管理与全寿命周期管理提供理论基础支撑，对规范保障房项目建设管理体制具有重要的实践意义。

1 保障房项目后评价相关概念与特点分析

保障房项目后评价是保障房项目建设管理的重要组成部分，主要指在保障房项目建设完成并已运行一段时间后，对保障房项目规划和建设的目的、建设过程、经济效益作用、环境影响以及社会影响进行全面客观分析与总结的一种技术经济评价活动［5，6］。将后评价过程中得到的反馈信息，作为未来社会保障项目决策的依据，为提高投资决策和建设管理水平提供参考，从而达到提高项目投资效益与社会效益的目的。保障性住房供应体系分析如图1所示。

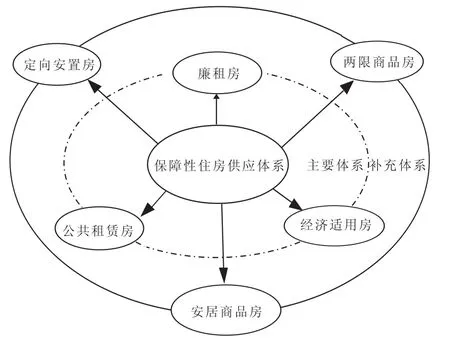
图1 保障房项目供应体系

从目前来看，在保障房项目全寿命周期过程中，同一类问题在不同项目或同一项目不同阶段反复出现，在增加决策和建设成本的同时，对政府公信力和开发商形象以及项目抗风险能力带来一些不利影响［7］。保障房项目后评价指标体系研究无论是投资额还是社会意义上，对我国民生项目市场影响深远。结合保障房项目的概念及特点，保障房项目后评价机构可以通过对保障房项目的经济效益、宜居性、社会效益和管理过程等进行全面的调查研究，在后评价基础上，找出偏差产生的原因并总结过程中的经验教训，通过有效的、系统的信息反馈机制，制订改进措施，并为今后类似的保障项目建设管理提供借鉴［8，10］。具体的保障房项目后评价体系反馈管理流程如图2所示。

图2 保障房项目后评价反馈管理流程

2 保障房项目后评价主要内容及初步指标体系构建

2.1 保障房项目后评价指标初选方法及专家选择

2.1.1 保障房项目后评价指标初步筛选方法

后评价指标中，一级、二级指标包含的内容相对比较宽泛，德尔菲法是最常用的方法［11］，但其存在主观随意性较大和对相关专家水平要求较高的缺点，保障房项目后评价又具有涉及专业领域广泛的特点，使得选取能够对后评价指标进行客观评判的保障房项目相关领域的专家非常困难，因此采用改进型的德尔菲法对一级、二级指标进行筛选。优点在于进行后评价指标重要程度评判时，不要求每个打分专家对所有指标进行评判，专家可依据其专业背景及擅长领域对其能够给出客观结果的后评价指标进行评判，从而提高了指标评判结果的准确性与合理性［12］。具体可将指标重要性划分为三级量表（表1）。

表1 指标重要性分级及分值

2.1.2 一级、二级指标评判专家的选取

后评价专家选取的数量、专业水平以及覆盖面直接影响指标体系的合理性、简约性与科学性，本文研究选取相关专家的标准是：

（1）保障房项目后评价涉及三个主要利益相关方，分别是政府、开发商和业主，因此选取的专家要能覆盖这三个方面的人员，数量要相对较多，分配要相对均衡；

（2）一级、二级指标筛选采用改进型德尔菲法时选取的专家应对保障项目建设管理及政府相关政策较为熟悉，且具备保障项目规划及项目管理知识背景，在相关领域工作10年以上且经验丰富。

本文严格按照上述两条标准选取相关专家16人，其中6人为重庆市建委及住保办相关专家、7人为从事过保障房项目建设的房地产开发企业管理人员、3人为具有保障项目投资及管理经验的业主。三级指标采用Rough Sets（粗糙集）理论计算指标偏离程度时，因对专家数量要求较高，在下文中会详细描述专家分布状态以及相关数量。

2.2 保障房项目后评价指标体系构建步骤

保障房项目后评价指标体系的构建过程是一个从具体到抽象再到具体的辩证逻辑思维过程，可分为以下三个环节：理论准备环节、指标体系初选环节、指标体系的优化环节。这样才能建立一套科学合理的后评价指标体系［13］。本文拟采用的具体过程如图3所示。

图3 后评价指标体系构建过程

2.3 保障房项目后评价指标筛选

二级指标体系对于所有保障房项目后评价来说基本都会涉及到，但由于不同的保障房项目客观条件存在一定差异，导致后评价三级评价指标侧重点也有所不同［14］。因此，在对保障房项目进行后评价的时候，必须针对不同项目的特点，由项目后评价的专家根据项目的实际情况进行指标体系调整。等级全息建模（HHM）的基本思想是：根据系统工程的基本原理，构建大规模的复杂系统，基于多个不同评价体系下包含多个层次的后评价指标等级全息模型。从不同的视角出发去识别保障房项目的后评价主要因素。需要首先把风险从一个整体划分为若干子系统，这种划分子系统的不同视角叫做识别维度，每个维度都代表了后评价系统的某个侧面，同时基于不同维度的子系统又包含了若干评价内容。基于HHM法可对三级后评价指标进行筛选分析，如图4所示。

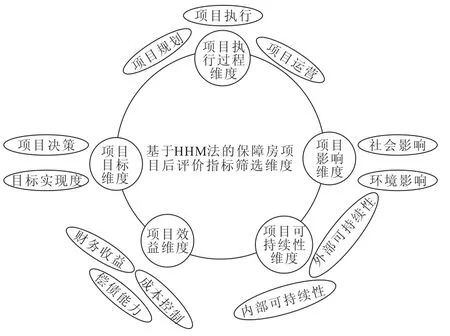
图4 基于HHM法的保障房项目后评价指标识别维度

2.4 保障房项目后评价指标体系初步构建

基于HHM法，可从项目目标、执行过程、项目影响、项目效益、项目可持续性五个维度对保障房项目的后评价指标进行识别与筛选［15］，结合2.1节中采用改进型的德尔菲法可得出保障房项目后评价指标，在此基础上可构建初步的保障房项目后评价指标体系（表2）。

表2 保障房项目后评价初步评价指标体系

3 基于Rough Sets理论的保障房项目后评级指标体系优化

3.1 指标体系优化方法选取

在构建保障房项目后评价指标体系时，需要遵循独立性、全面性、协调性与可行性的原则。后评价指标个数较多，则各个指标之间包含的信息可能发生重叠，影响指标的独立性；反之后评价指标越少，则其独立性会更好，但会影响其全面性［16］。因此，需要在指标体系的全面性与独立性之间进行优化，以寻求平衡。后评价指标在有统计数据（如财务数据、投资收益率）时，则数据条件方差极小法、广义不相关法等方法应用较多；对既包含定性指标又包含定量指标的后评价指标体系时，则定量指标可依据统计数据，而没有统计数据的定性指标则需要有一定的专业知识积累的相关专家来根据从业经验主观评判指标的重要度。

在进行保障房项目后评价指标体系的约简时，运用Rough Sets理论方法则可兼顾定量指标的客观性和定性指标的主观性，Rough Sets理论相比其他方法具有较好的鲁棒性与知识数据挖掘功能，能精确地处理部分需要专家主观判断的问题；其次，Rough Sets理论可以从小样本数据中计算出指标相互之间的依赖关系，且具备发掘冗余指标，构建最精简指标集合的特点。因此本文在构建保障房项目后评价指标体系时，将结合Rough Sets理论对指标体系进行优化。根据Rough Sets理论的应用原理，其首先需要对前期收集到的基础打分数据进行离散化处理并形成决策表，然后将离散化处理后的相关数据运用Excel数据表的格式导入Rosetta计算软件，然后利用遗传算法对保障房项目后评价指标进行归类与约简，计算各后评价指标的偏离程度，对偏离程度大于90%的指标进行约简与删除处理，从而得到优化之后的指标。

3.2 Rough Sets理论假设与范围界定

Rough Sets理论进行后评价指标体系中各指标偏离程度的计算时，常用的方法如图5所示：

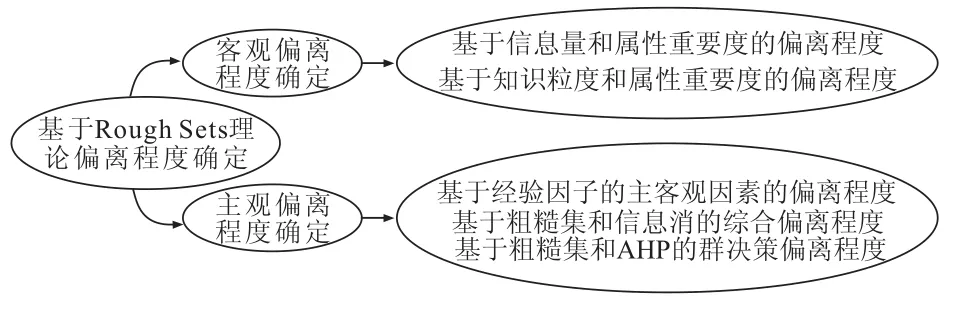
图5 基于Rough Sets理论的指标偏离程度确定

本文中后评价指标体系优化采用基于知识粒度与属性重要度的Rough Sets理论计算方法，具体Rough Sets计算理论定义如下所示：

定义1 设P和Q是U上的等价关系族，R∈P。决策表中等价类关系集合表示为Ind（P），POSInd（P）表示子系统P根据族元素相似关系得出的每种分类结果。若：系统子集满足 POSInd（P）（Ind（Q））=POSInd（F-（R））（Ind（Q）），则称族P-｛R｝为P的Q相对约简，即族P-｛R｝在族集P中Q是可省的，否则称为Q是不可省的；如果在族P中的每个关系R都是Q不可省的，则称P关于Q是独立的，否则称其是依赖的。

定义2 知识系统可以定义为一个四维集合函数S=（U，R，V，f），其中U=｛x1，x2，…，xn｝表示通过问卷调查获得的样本数据，为集合的论域，R是各个指标属性的非空有限集合，Va是属性的值域，即是U×R→V的一个信息函数，它为每个对象xi的每个属性赋予一个属性值，即a∈R，x∈U，fa（x）∈Va。

定义3 设S=（U，R，V，f），R=C∪D，C∩D =Ø，C为条件属性，D为决策属性集，记作T=（U，R，C，D）或称为C、D的决策表。

定义4 S=（U，R，V，f）是一个信息系统，P，Q⊆R，则可以定义属性r在指标体系中的重要度为：

可以定义指标属性r在指标体系中的权重为：

可以定义指标属性r在指标体系中的偏离度为：

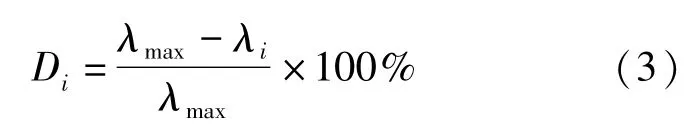
式中：U为待评价的对象集；P、Q为待评价指标体系的子集合，或者待评价对象集的等价关系族；λ为指标权重。重要度ur越大，则表示指标r对指标集的贡献越大；若重要度ur=0，表示指标r在指标集中是冗余的。通常对打分问卷进行整理，进行数据离散化预处理，计算后评价指标在指标集中的重要度、权重以及偏离度，对于偏离度Di大于90%的指标通常需作约减处理，最终可以得到优化后的保障房项目后评价指标体系。

3.3 基于Rough Sets理论的保障房项目后评价指标体系的优化计算

调查问卷主要采用Likert-Scale表的形式，1级至5级表示影响程度逐渐变大，其中1代表后评价指标对保障房项目后评价根本无影响，5代表后评价指标对保障房项目后评价影响程度特别重要［17］。针对构建的初选保障房项目后评价指标体系集，设计了“保障房项目后评价指标影响程度调查问卷”。为了确保能够反映出后评价指标与保障房项目的相关程度的真实情况，接受问卷调查的专家必须是具有丰富保障房项目从业经验以及研究经验，从而使本次调查具有很强的可靠性和代表性。具体调查对象组成如图6所示：

图6 保障房项目后评价指标体系调查对象组成

其中，政府单位、建设单位、施工单位和监理等单位的调查人数占到了本次调查人数的78%，基本能够涵盖保障房项目领域的专业人员，也使得本次调查的数据更加科学有效，最终收集到的有效问卷为57份（一共63份，其中6份为无效问卷）。下面以保障房项目社会影响后评价指标层的指标体系优化计算为例。

3.3.1 构建保障房项目后评价指标体系决策表

构建保障房项目后评价指标体系计算决策因素表：如上文定义3.2中所示，S=（U，R，V，f），其中U=｛x1，x2，x3，…，xj｝，j=1，2，3，4，5，6，7为论域；V是指标属性打分值A的集合，Va是指标属性的值域，即是U×A→V的一个信息函数，它为每个对象xi的每个属性a赋予一个属性值，即a∈A，x∈U，fa（x）∈Va。

其中，A1，A2，A3，A4，A5，A6，A7分别对应上文表2中保障房项目后评价初步指标体系中的促进社会和谐、改善就业现状、提高城市化水平、提高建筑企业知名度、抑制房价过快增长、促进经济发展、增强社会文化适应性；xj为通过回收的57份有效问卷中所统计到的对应打分信息。用Aij表示第j份问卷中Ai指标的分数，即调查的结果。整理汇总后即可得到保障房项目社会影响后评价指标集决策表，因文章篇幅有限，具体的调查问卷数据不详细列出。

3.3.2 指标体系等价类关系集及其正域的求解

对于保障房项目社会影响后评价指标层A来说，S=〈U，A〉，其中论域U=｛1，2，3，4，5，6，7｝，条件属性A= ｛A1，A2，A3，A4，A5，A6，A7｝。根据Rough Sets理论等价类集合以及正域的定义，求出条件属性A的等价类集合与集合正域，结果如下：

U/Ind（A）=｛｛1，26｝，｛2｝，｛3｝，｛4｝，｛5｝，｛6｝，｛7，27，36｝，｛8，51｝，｛9｝，｛10｝，｛11｝，｛12｝，｛13，29｝，｛14｝，｛15，54｝，｛16｝，｛17｝，｛18｝，｛19｝，｛20｝，｛21｝，｛22，46｝，｛23｝，｛24｝，｛25｝，｛28｝，｛30｝，｛31｝，｛32｝，｛33｝，｛34｝，｛35｝，｛37｝，｛38｝，｛39，44｝，｛40｝，｛41｝，｛42｝，｛43｝，｛45｝，｛47｝，｛48｝，｛49｝，｛50｝，｛52｝，｛53｝，｛55｝，｛56｝，｛57｝｝；

U/Ind（A1）=｛｛1，26｝，｛2｝，｛3｝，｛4｝，｛5｝，｛6｝，｛7，27，36，41｝，｛8，51｝，｛9，17｝，｛10｝，｛11｝，｛12｝，｛13，29｝，｛14｝，｛15，54｝，｛16｝，｛18｝，｛19｝，｛20｝，｛21，48｝，｛22，46｝，｛23｝，｛24｝，｛25｝，｛28｝，｛30｝，｛31｝，｛32｝，｛33｝，｛34｝，｛35｝，｛37｝，｛38｝，｛39，44｝，｛40｝，｛42｝，｛43｝，｛45｝，｛47｝，｛49｝，｛50｝，｛52｝，｛53｝，｛55｝，｛56｝，｛57｝｝；

U/Ind（A2）=｛｛1，26｝，｛2｝，｛3｝，｛4｝，｛5｝，｛6｝，｛7，27，36｝，｛8，51｝，｛9｝，｛10，42｝，｛11｝，｛12，34｝，｛13，29，48｝，｛14｝，｛15，54｝，｛16｝，｛17｝，｛18｝，｛19，20｝，｛21｝，｛22，46｝，｛23｝，｛24｝，｛25｝，｛28｝，｛30｝，｛31｝，｛32｝，｛33｝，｛35｝，｛37｝，｛38｝，｛39，44｝，｛40｝，｛41｝，｛43｝，｛45｝，｛47｝，｛49｝，｛50｝，｛52｝，｛53｝，｛55｝，｛56｝，｛57｝｝；

U/Ind（A3）=｛｛1，13，26，29｝，｛2｝，｛3｝，｛4｝，｛5｝，｛6｝，｛7，27，36｝，｛8，23，51｝，｛9，50｝，｛10｝，｛11｝，｛12｝，｛14｝，｛15，54｝，｛16｝，｛17｝，｛18｝，｛19｝，｛20，40｝，｛21｝，｛22，46｝，｛24｝，｛25｝，｛28｝，｛30｝，｛31｝，｛32｝，｛33｝，｛34｝，｛35｝，｛37｝，｛38｝，｛39，44｝，｛41｝，｛42｝，｛43｝，｛45｝，｛47｝，｛48｝，｛49｝，｛52｝，｛53｝，｛55｝，｛56｝，｛57｝｝；

U/Ind（A4）=｛｛1，26｝，｛2｝，｛3｝，｛4｝，｛5｝，｛6｝，｛7，27，36｝，｛8，51｝，｛9｝，｛10｝，｛11｝，｛12｝，｛13，29｝，｛14｝，｛15，54｝，｛16｝，｛17｝，｛18｝，｛19｝，｛20｝，｛21｝，｛22，46｝，｛23｝，｛24｝，｛25｝，｛28｝，｛30｝，｛31｝，｛32｝，｛33｝，｛34｝，｛35｝，｛37｝，｛38｝，｛39，44｝，｛40｝，｛41｝，｛42｝，｛43｝，｛45｝，｛47｝，｛48｝，｛49｝，｛50｝，｛52｝，｛53｝，｛55｝，｛56｝，｛57｝｝；

U/Ind（A5）=｛｛1，26｝，｛2｝，｛3｝，｛4｝，｛5｝，｛6｝，｛7，27，36｝，｛8，51｝，｛9｝，｛10｝，｛11｝，｛12｝，｛13，29｝，｛14｝，｛15，54｝，｛16｝，｛17｝，｛18｝，｛19｝，｛20｝，｛21｝，｛22，46｝，｛23｝，｛24｝，｛25｝，｛28｝，｛30｝，｛31｝，｛32｝，｛33｝，｛34｝，｛35｝，｛37｝，｛38｝，｛39，44｝，｛40｝，｛41｝，｛42｝，｛43｝，｛45｝，｛47｝，｛48｝，｛49｝，｛50｝，｛52｝，｛53｝，｛55｝，｛56｝，｛57｝｝；

U/Ind（A6）=｛｛1，26｝，｛2｝，｛3｝，｛4｝，｛5｝，｛6｝，｛7，15，27，36，54｝，｛8，51｝，｛9｝，｛10｝，｛11｝，｛12，39，44｝，｛13，29｝，｛14，21｝，｛16｝，｛17｝，｛18，31｝，｛19｝，｛20｝，｛22，46｝，｛23｝，｛24，49｝，｛25｝，｛28｝，｛30｝，｛31｝，｛32｝，｛33｝，｛34｝，｛35，56｝，｛37｝，｛38｝，｛40｝，｛41｝，｛42｝，｛43｝，｛45｝，｛47｝，｛48｝，｛50｝，｛52｝，｛53｝，｛55｝，｛57｝｝；

U/Ind（A7）=｛｛1，26｝，｛2｝，｛3，21｝，｛4｝，｛5｝，｛6｝，｛7，27，36｝，｛8，51｝，｛9｝，｛10｝，｛11｝，｛12｝，｛13，29｝，｛14｝，｛15，54｝，｛16｝，｛17｝，｛18｝，｛19｝，｛20｝，｛22，46｝，｛23｝，｛24｝，｛25｝，｛28｝，｛30｝，｛31｝，｛32，56｝，｛33｝，｛34｝，｛35｝，｛37｝，｛38｝，｛39，44｝，｛40｝，｛41｝，｛42｝，｛43｝，｛45，57｝，｛47｝，｛48｝，｛49｝，｛50｝，｛52｝，｛53｝，｛55｝｝。

由此可得：U/Ind（A）=U/Ind（A-｛A4｝=U/ Ind（A-｛A5｝）≠U/Ind（A-｛A1｝）≠U/Ind（A-｛A2｝）≠U/Ind（A-｛A3｝）≠U/Ind（A-｛A6｝）≠U/Ind（A-｛A7｝），由Rough Sets约简理论可知，提高建筑企业知名度（A4）、抑制房价过快增长（A5）是冗余因素，其他剩余指标如：促进社会和谐（A1）、改善就业现状（A2）、提高城市化水平（A3）、促进经济发展（A6）、增强社会文化适应性（A7）均不是冗余因素，不能进行约简。具体约简提高建筑企业知名度与抑制房价过快增长哪个指标以及具体的约简方式可通过下面的算例计算得到。

3.3.3 后评价指标因素依赖度的计算

根据基于知识粒度与属性重要度的Rough Sets理论计算方法，通过公式（1）以及3.3.2节中得到的等价类关系集合计算各个后评价指标的重要度为：

3.3.4 后评价指标权重的确定

根据上文公式（2）计算可得：

λA1=0.166；λA2=0.173；λA3=0.238；

λA4=λA5=0.018；λA6=0.327；λA7=0.069。

3.3.5 计算各指标的偏离程度进行指标约简

根据上文公式（3），计算指标属性A=｛A1，A2，A3，A4，A5，A6，A7｝的偏离程度，结果如下所示：100%=78.90%。

同理根据以上步骤可以求得表2中所有后评价指标的重要度、权重以及偏离程度，将计算结果汇总即可得表3。

表3 保障放项目后评价指标计算汇总

3.4 优化后的保障房项目后评价指标体系

根据基于知识粒度与属性重要度的Rough Sets理论，按照偏离度大于90%的原则进行保障房项目后评价指标的约简，有12个初步指标被约简，包括初步设计、工艺设施建设水平、资金与物质落实工作、竣工验收工作质量、提高建筑企业知名度、抑制房价过快增长、维持景观能力、流动比率、项目兼容能力、项目竞争能力、项目内部支持能力、项目与区域发展的影响，剩下的指标已相对完整地构成了保障房项目后评价指标体系，为以后的保障房项目后评价工作奠定了一定的科学理论与实践基础。优化后的保障房项目后评价指标体系如图7所示。

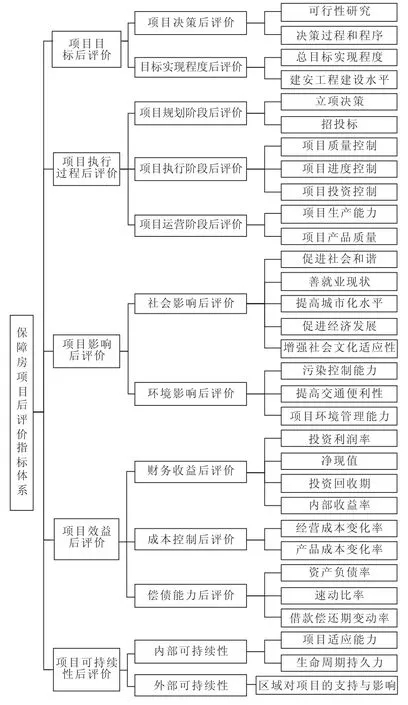
图7 优化后的保障房项目后评价指标体系

4 结 语

建立一套科学合理的保障房项目后评价指标体系以及与指标体系相适应的指标优化筛选方法一直是近些年相关领域研究的重点。本文通过HHM法并结合相关研究文献从不同维度对保障房项目后评价主要评价指标的识别与筛选，得出了初步的保障房项目后评价指标体系。在此基础上，通过改进型的德尔菲法对初步指标进行剔除。其次，通过发放问卷的形式，收集了针对初步保障房项目后评价指标体系的打分数据。然后利用基于知识粒度与属性重要度的Rough Sets理论计算方法，剔除与约简了偏离程度较大的12个冗余的初步保障房项目后评价指标，建立起了更加科学合理的符合保障房项目固有特点的后评价指标体系，以期为以后的保障房项目投资决策、建设管理、后评价管理等提供一定的理论与实践指导依据。

［1］贾乐盈.保障性住房建设项目后评价指标体系研究［J］.价格月刊，2014，（10）：87-90.

［2］胡 杰，李子侠，韩 冬，等.我国保障性住房项目后评价体系构建思路——基于过程绩效的视角［J］.中国房地产，2014，（18）：41-46

［3］晏 姿，岳静宜，郝生跃.保障性住房综合评价体系构建研究——基于核心利益相关者视角［J］.工程管理学报，2014，28（6）：129-133.

［4］邓中美.社会保障性住房制度评价指标体系研究［J］.重庆科技学院学报（社会科学版），2009，（8）：96-97.

［5］张占斌，李万峰，费友海，等.中国城镇保障性住房建设研究［M］.北京：国家行政学院出版社，2013.

［6］朱莉萍.城镇住房保障水平研究——以北京市为例［D］.上海：同济大学，2008.

［7］王 盛，旷丽军.保障房市场与商品房市场关系研究［J］.科学发展，2013，（12）：76-84.

［8］王广浩.建设项目后评价内容完善与方法研究［D］.杭州：浙江大学，2004.

［9］李志清，田金信.北京市保障性住房供给预测研究［J］.哈尔滨工业大学学报（社会科学版），2009，11（5）：89-94.

［10］林莉杉.赣州市保障性住房建设、运营和管理机制研究［J］.科技广场，2012，（8）：166-168.

［11］Dukic D，Maric T，Babic D.Analysis of Duration and Cost Estimate of Construction Projects Through Computer Simulation［C］//2007 29th International Conference on Information Technology Interfaces.Piscataway，NJ：IEEE，2007：107-112.

［12］王立里，蒋泽熙.一般住宅项目后评价指标体系研究［J］.经济论丛，2010，（5）：256.

［13］李远远.基于粗糙集的指标体系构建及综合评价方法研究［D］.武汉：武汉理工大学，2009.

［14］Kim G H，Yoon JE，An SH，et al.Neural network model incorporating a genetic algorithm in estimating construction costs［J］. Building and Environment，2004，39（11）：1333-1340.

［15］李 娟.基于政府财政能力的住房保障适度水平研究——以南京市为例［J］.中国房地产金融，2008，（1）：41-44.

［16］Chen S，Ravallion M.Hidden Impact？ex-post evaluation of an anti-poverty program［J］.Development Research Group World Bank，2003，（5）：220-233.

［17］杜俊慧.固定资产投资项目后评价方法研究——基于不确定理论的视角［M］.北京：经济管理出版社，2012.

Optim ization of Post Evaluation Index System in Affordable Housing Projects Based on Rough Sets Theory

WANG Bo
（Department of Tourism and Service Management，Chongqing University of Education，Chongqing 400040，China）

Affordable housing projects are an important part of the social security system，which affects livelihood and social harmony.Firstly，it analyzes themain contents and characteristics of the post evaluation in affordable housing projects.Then it identifies and screens the post evaluation index of affordable housing projects from objectives，implementation process，project impacts，project benefits，sustainability by usingmodified Delphimethod and HHM method.Based on the knowledge size and attributed importance of Rough Sets theory，it calculates important indicators、index weights and extent of deviation，excluding the reduction of redundancy greater degree deviation indicator，excluding the redundancy index which has greater degree of deviation.After that，a more scientific and reasonable evaluation index system is established with inherent characteristics to provide a basis for the study on post evaluation and life-cyclemanagement of future affordable housing projects.

affordable housing projects；post evaluation；optimization of index system；knowledge size；rough sets theory

F293.3；F224.7

A

2095-0985（2016）04-0068-08

2015-12-28

2016-02-24

王 波（1983-），女，四川雅安人，讲师，硕士，研究方向为保障房项目建设管理及后评价管理、房地产及物业评价管理、工程经济（Email：zjd107@aliyun.com）