K近邻算法在雷达信号识别中的应用

徐 晔，李宝双

(中国船舶重工集团公司第723研究所，扬州 225001)



K近邻算法在雷达信号识别中的应用

徐 晔，李宝双

(中国船舶重工集团公司第723研究所，扬州 225001)

介绍了机器学习算法中的K近邻算法，讨论了该算法在雷达信号识别中的应用，用python语言实现了雷达识别程序，并分析了得到的结果，阐述了对算法结果产生影响的几方面内容。

K近邻算法；python语言；雷达信号识别

0 引 言

雷达信号识别是在信号分选的基础上，根据得到的雷达射频、重频、脉宽等信息，与数据库中的已知信息进行比对，从而得到雷达的名称、平台、型号等信息的过程。雷达信号识别的结果为决策机构提供了相关敌对方雷达的工作方式、平台类型、威胁程度等信息，是指挥判断的重要依据。雷达识别的一般流程如图1所示。

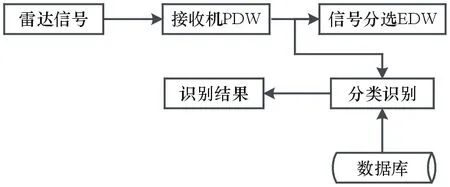
图1 雷达识别的一般流程图

雷达信号识别有多种方法，如现在使用的最大隶属度法、模板匹配法等。本文使用的K近邻算法属于机器学习算法的一种。

1 K近邻算法概述

雷达信号识别的目的就是根据特征对目标雷达进行分类，机器学习中有多种方法进行分类，其中的K近邻算法属于学习方法中的一种，因为该类算法需要明确知道目标变量的分类信息，所以被称为监督学习算法，否则被称为无监督学习算法。K近邻算法的工作原理是：存在一个样本数据集合，称之为训练样本集，样本中的每一数据都有自己的分类标志，即样本中的数据都明确地对应一个所属的分类。当新输入的数据没有明确的分类标志时，将该数据的特征与样本集中数据的特征进行比较，然后算法提取相似度最高的数个数据的分类标志，以此来确定新输入数据的类型。一般情况下取前K个最相似数据中出现次数最多的分类标志，并将其作为未知信号的分类。

K近邻算法的一般流程如下：

(1) 收集数据：可以使用多种方法收集数据。

(2) 准备数据：找到需要的特征值，将数据进行格式化。

(3) 测试算法：计算错误率。

(4) 使用算法：首先需要输入样本数据和结构化的输出结果，然后运行K临近算法判定输入数据分别属于哪个分类，最后对计算出的分类进行后续处理。

K近邻算法的优缺点及适用范围：

优点：精度较高，对异常值不敏感，无数据输入假定。

缺点：时间、空间复杂度较高。

K近邻算法可适用于数值型等类型数据。

2 在雷达识别中使用K近邻算法

2.1 参数和测量方法的选取

在雷达识别中使用K近邻算法，第1步需要收集数据，可使用预设置的雷达信号参数，第2步是确定数据的特征值并对其进行格式化。当前情况下，信号分选可提供的参数主要有雷达的射频类型、射频值、重频类型、重频值、脉宽值、方位、幅度这几种。根据经验可知，方位值及幅度值受单次测量影响较大，无法作为识别的依据。因此，选取射频、重频、脉宽3个值作为雷达信号识别的特征值。计算特征值间的距离时，使用欧氏距离进行计算：

(1)

2.2 编程环境及语言的选择

为方便编程，选用python语言对数据进行处理。python语言语法较简单，且可以操作多种高级数据类型，这些类型可以简单地实现抽象的数学概念，在python中可以使用Numpy库和Matplotlib库完成矩阵操作和绘图操作。这2个库在编程中都有应用。

2.3 算法实现

2.3.1 数据采集

算法实首先需要收集数据，将15部预先设好的雷达参数存放在文本文件中由程序读出。数据存放在radar.txt 中，每行顺序存放射频值、重频值、脉宽值、雷达名称4项，以换行符为分隔符，每行数据代表1部雷达的1次测量数据。文件中每部雷达有5组测量数据，共有75组测量数据。数据限于篇幅不全部列出，仅对每部雷达取1组数据列出，如表1所示。

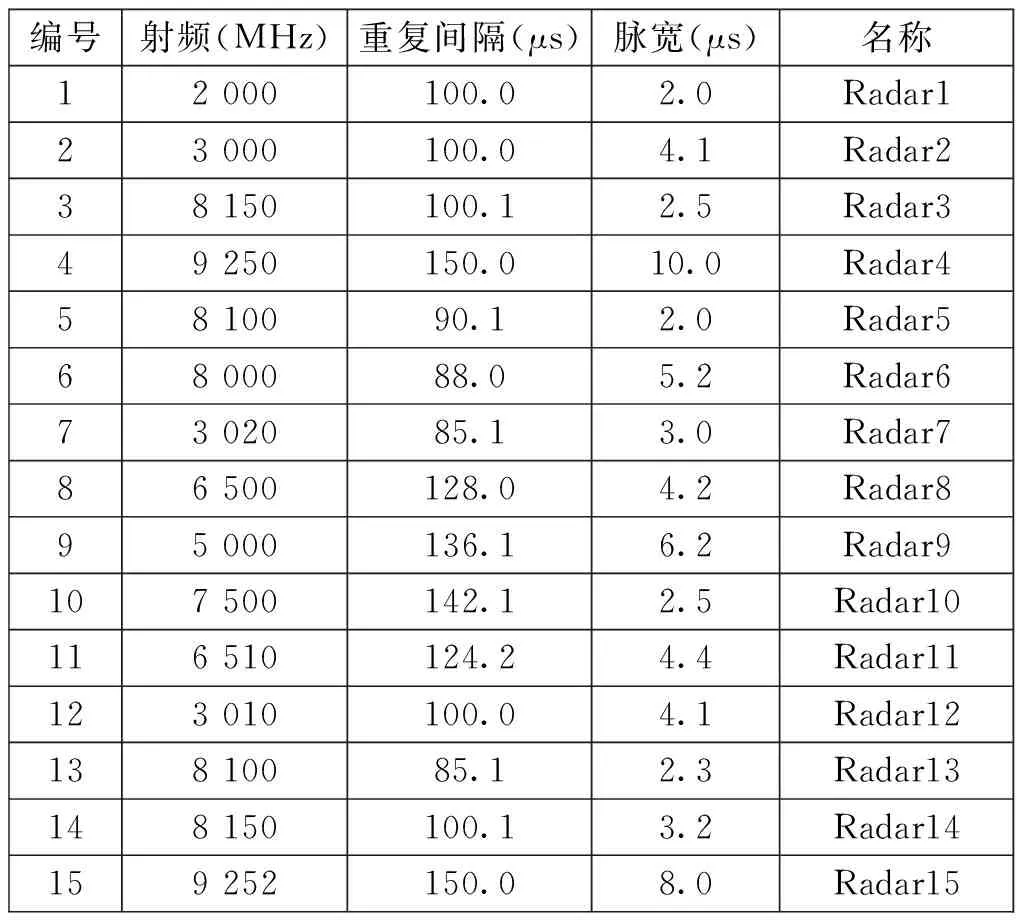
表1 雷达参数表

然后需要对数据进行处理，由于频率参数绝对值较大，直接代入计算将会导致该分量所占比重过大，因此需要对参数进行归一化处理。15部雷达的数据点分布如图2～图4所示。图2为射频-重复间隔关系图,图3为重复间隔-脉宽关系图,图4为射频-脉宽关系图。

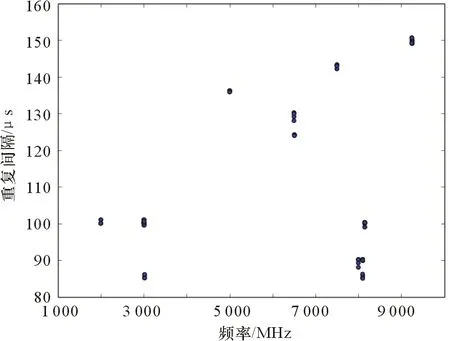
图2 射频-重复间隔关系图

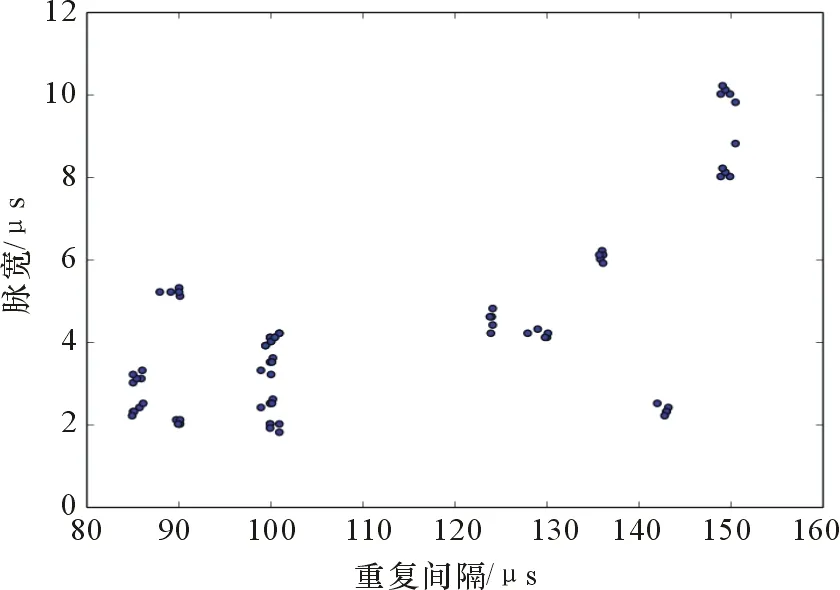
图3 重复间隔-脉宽关系图

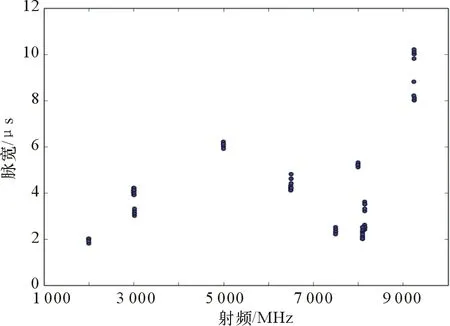
图4 射频-脉宽关系图

2.3.2 算法实现及应用

算法流程图如图5所示。

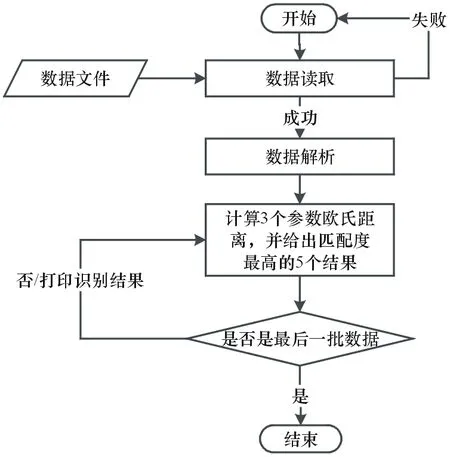
图5 射频-脉宽关系图

将文本文件中的数据读入内存，根据要求，编写了Filetomatrix函数，代码如下：

def Filetomatrix (filename):

Fp=open (filename)

Lines=fp.readlines()

returnMat=zeros((len(Lines),3))

LabelVector=[]

Index=0

For line in Lines

Line=line.strip()

Listfromline=line.split(' ')

retunrMat[index,:]=listFromLine[0:3]

LabelVector.append(int(listFromLine[-1]))

Index+=1

return returnMat,LabelVector

首先打开文件，并得到文件的行数，也就是记录数，然后创建返回的Numpy特征矩阵，并将其置0。Strip函数用来截取所有的回车符，并用' '字符将得到的整行数据分割成一个元素列表,最后将文件内容解析到该矩阵中。由于最后一个元素是雷达名称，所以选取前3个元素存储到特征矩阵中。

读取数据完成后，将数据集中的每条记录与数据集分别进行计算，得到每条数据的分类结果，最后计算正确率。源代码如下：

def idetify():①

Errnum=0.0

radardataMat,radarLabels,radarlines=Filetomatrix(‘radar.txt’)②

numberofLines=len(radarlines)③

normMat,ranges,minVals=autoNorm(radarDataMat)④

for index in range(numofLines)

calssResult=classfy(normMat[index],norMat,radarLabels,3)⑤

Print calssResult

If classResult !=radarLabels[index]:

Errnum +=1⑥

return calssResult

第①步，定义函数；第②步，将数据从文件中读入特征矩阵中；第③步，读取记录条数；第④步，将数据归一化；第⑤步，循环读入每条数据进行比对，并将结果打印出来；第⑥步，计算识别的正确率。

当K值取3 时，识别结果的错误率为1.3%；当K值取为4时，识别结果的错误率为2.6%；当K值取5时，识别结果的错误率为0。表2为K=5时的识别结果。

表2中第3列表示关联度最高的雷达类型出现次数，可以看到，在参数相似的情况下，识别结果会出现一定的波动，但综合后仍能给出正确结果。

3 结果分析

根据程序实现可知，对识别结果产生影响的主要有以下几个方面：

(1)K的取值。K值大小对识别结果有一定的影响，取得太大，会导致计算量过大；取得太小，可能造成异常情况的出现，从而影响识别结果。

(2) 样本数量。样本数量本身也会对识别结果造成影响，样本数量过多，容易造成重复计算，影响识别速度；数量过少，则不能完全代表某类数据，造成识别失败。

表2 K=5识别结果

(3) 特征值数量。特征值的选取是识别中最重要的一环，特征值是识别的依据，因此必须是独特的，能完全描述被测量信息的真实值，并且该值不会随外界环境而改变。在雷达信号识别中，选取的射频、重频、脉宽值都符合上述要求，而同是测量参数的方位、幅度等因受外界环境影响较大，不能作为特征值使用。在信号处理产生的信息中，信号参数类型也是一类特征值，但该特征值会受到信号处理算法正确率的影响，不能完全置信。因此，若需要在算法中将参数类型作为特征值处理时，可以通过将参数类型数据化，并修改其在算法中的比重来修正对识别结果的影响。

4 结束语

雷达识别是一项系统工程，特征参数的选取、信息收集、前端数据测量精度等都会影响到识别结果，K近邻算法作为一种监督学习算法有实现简单、精确度高、对异常值不敏感等优点，在雷达信号识别中可以快速，正确地完成工作，同时由于K近邻算法需要多次运算，因此在工程实践中需要更好的优化以达到最佳效果。

[1] CONWAY D，WHITE J M.机器学习：实用案例解析[M].陈开江，刘逸哲，孟晓楠译.北京:机械工业出版社，2013.

[2] HETLAND M L.python基础教程[M].2版.司维，曾军崴，谭颖华译.北京:人民邮电出版社,2010.

Application of KNN Algorithm to Radar Signal Recognition

XU Ye,LI Bao-shuang

(The 723 Institute of CSIC,Yangzhou 225001,China)

This paper introduces the K-nearest neighbor (KNN) algorithm in machine learning algorithms，discusses the application of KNN algorithm to radar signal recognition,realizes the radar recognition program with python language,and analyzes the results,expatiates several factors influencing the algorithm results.

K-nearest neighbor algorithm;python language;radar signal recognition

2016-05-23

TN971.1

A

CN32-1413(2016)04-0056-03

10.16426/j.cnki.jcdzdk.2016.04.013