高速火箭弹不同防热方案对气动加热影响规律的研究

周宇航，张向洪，张 敏

(南京理工大学 能源与动力工程学院，南京 210094)



【装备理论与装备技术】

高速火箭弹不同防热方案对气动加热影响规律的研究

周宇航，张向洪，张 敏

(南京理工大学 能源与动力工程学院，南京 210094)

采用工程算法与数值算法相耦合的气动热计算方法进行高超声速火箭弹的气动热参数计算。对火箭弹边界层外缘参数采用无黏数值算法求取，对边界层内黏性起主导作用的区域采用工程算法计算。由于防热层厚度方向特征尺寸远小于火箭弹表面特征尺寸，对防热层的气动热计算进行了一维简化并建立了一维非稳态导热微分方程。在确定防热层边界条件后，经过导热微分方程的求解得到了长航状态下火箭弹防热层的温度分布。通过对防热层的不同物性参数的研究，得出防热层物性参数对气动加热的影响规律，为气动热防护问题的研究提供了参考。

防热层；数值算法；工程算法；高超声速；气动热参数

随着科学技术的迅猛发展，高新技术在兵器研制中得到广泛应用，武器的性能获得大幅度的提高，获得战争的胜利不再是取决于武器数量的多少，更多的是取决于武器质量优劣[1-3]。高超声速火箭弹一般是指以吸气发动机或组合发动机为动力，在大气层内和跨大气层中飞行速度大于5马赫的火箭弹，高超声速武器是当今世界主要军事强国发展的重点[4-6]。

高超声速火箭弹的气动特性、气动加热和大气干扰会引起基础结构失真、模型和参数不确定等一系列问题。高超声速飞行对火箭弹的气动性能以及防热提出了更高的要求[7]，对此承担着火箭弹气动热防护主要任务的防热层起着至关重要的作用。而防热层的物性参数选取直接决定了防热层的热防护效率，本研究对防热层的不同物性参数进行研究，得出不同物性参数对气动加热的影响规律。

高超声速火箭弹在飞行过程中表面温度随着时间的推进不断增加直至进入热稳态。对于高超声速飞行器进入稳态状况后，热流密度越大的区域温度越高，并在驻点达到温度最大值。由于驻点温度很高极易产生烧蚀影响火箭弹的稳定飞行，因此在火箭弹表面添加防热层可以延缓表面的温度升高速率，延长火箭弹达到热稳态的时间。防热层不同的物性参数材料的选取直接决定了火箭弹的温升速率。本文采用数值算法与工程算法相耦合的计算方法求解火箭弹表面的气动热参数[8]。在火箭弹表面的气动热参数确定后，采用非稳态导热微分方程的中心差分格式计算长航状况下防热层温度分布。根据非稳态状况防热层的温度分布分析物性参数对气动加热的影响[9-10]。

1 高超声速火箭弹表面和防热层气动热参数计算方法

工程计算中将火箭弹表面气动热分为两部分：一部分为非驻点区域气动热计算，由于对火箭弹模型进行了简化，本文采用平板热流密度公式进行非驻点区域气动热计算；另一部分为驻点区域气动热计算，采用Fay-Riddell驻点热流密度计算公式计算驻点热流密度[11]。

本文边界层外缘无黏区域数值计算，边界层内黏性主导区域采用工程算法计算火箭弹表面气动热参数[12]。在计算防热层温度分布前，对火箭弹物理模型进行简化：因为防热层的厚度尺寸远小于飞行器物面尺寸，将整个火箭弹防热层看作一维平板。对于一维平板非稳态导热，采用一维非稳态导热微分方程的中心差分格式计算长航状况下防热层温度分布[13-14]。

1.1 驻点气动热分析

火箭弹在飞行过程中前缘出现速度为零且静压达到最大值的点，在空气动力学上叫做驻点。由于驻点处气流压缩现象最为强烈，往往形成剧烈的气动加热，因此驻点的气动热计算和分析至关重要。依据驻点的定义通过如下的算法确定驻点位置：对于四边形网格，通过Fluent求解器输出的格点速度矢量求解出两个格点所在边的速度矢量，同理确定剩余边的速度矢量。对于四边形网格，若四条边界上的速度方向都指向四边形外侧，那么这个点可以判断为驻点。驻点热流密度与边界层外缘参数的关系为

(1)

式中：Pr为普朗特数，取0.7；Le为路易斯数，取1.4；Rn为研究对象的球头半径；(due/ds)s为驻点处速度梯度；hD为空气平均离解焓。

1.2 平板气动热计算

高超声速火箭弹非驻点区域的传热系数计算，目前主要通过经验公式计算并加以修正[14]。对于可压缩流首先转换简化为不可压缩流求解，再通过雷诺比拟把斯坦顿数和表面摩擦因数联系起来转换到可压缩流[15]。对于压缩效应，采用Eckert参考焓进行修正。从而得到了平板气动热的求解公式

(2)

式中： ρe为边界层外缘密度； μe为边界层外缘速度； ρ*、 μ*在得到参考焓后根据气体热力学特性求出。

在整个火箭弹表面的热流密度确定后，在非稳态状况下防热层内部边界条件为绝热边界条件，防热层外部边界条件为热流边界条件，可以进行火箭弹的防热层导热计算。

1.3 防热层的气动热参数计算

根据能量守恒定律与傅里叶定律建立物体的温度场应当满足的关系式称之为导热微分方程。导热微分方程是满足所有导热物体的通用方程

(3)

(4)

式中α=λ/ρc称为热扩散率或热扩散系数。在简化了导热微分方程后，采用有限差分方法求解防热层温度分布。首先对平板的厚度L方向进行离散化，得到

(5)

Δx=xi+1-xi作为空间步长，显然xi=(i-1)Δx。

对于时间离散采取同样的离散方式。为了区别于空间步长，这里使用n作为标示。

(6)

时间步长Δτ=τn-τn-1，显然τn=nΔτ。

将式(4)用于平板i点上第n时刻，可以得到

(7)

对于左侧非稳态项用一阶差分，对于右侧扩散项采用二阶中心差分有

(8)

整理后有

(9)

(10)

经过上述推导，得到了下一个时刻节点温度与上一时刻节点温度关系，当时间条件与边界条件得到确定后就可以得出整个防热层的温度分布。

对于具体的问题，还需要确定相应的时间条件与边界条件以满足方程的求解。对于防热层导热计算，本文使用的初始时间条件T(x,0)为已知定值。边界条件为第二类边界条件，即热流边界条件。防热层外缘的热流q1为平板热流密度，即q1=qw。平板内侧的热流密度q2在非稳态情况下，假设为q2=0。将边界条件应用于傅里叶导热定律，则每一时刻边界温度有如下关系。

(11)

2 高超声速火箭弹表面气动热参数的算例验证

本文使用D-5450钝锥模型，对飞行器表面气动热参数进行验证。

在NASA TN D-5450报告中，Joseph W.Cleary等做了一系列风洞实验，并整理了15度的钝锥层流热流密度，在这里选取该模型进行算例验证。设置求解条件，飞行状态为零攻角，大气压p∞=132 Pa，空气温度T∞=47.34 K，来流空气速度Ma∞=10.6。该模型尺寸如图1所示。

图1 模型尺寸

在确定了求解对象后，进行网格的划分。网格划分决定了在Fluent求解器的求解精度。本文划分的网格有节点9 594个、四面体单元9 321个。由于求解对象的外形决定头部气动加热最为明显，所以在划分网格时对研究对象的头部网格密度加大，保证了头部所得解的精度。划分完成后的网格示意图如图2。

图2 弹体网格和头部网格

将网格输入至Fluent求解器，按上述求解条件设置参数，得到收敛结果如图3和图4所示。

图3 钝锥压力云图

图4 钝锥密度云图

图中较清晰地捕捉到了弓形脱体激波。由压力分布可以看出头部的压强急剧上升，空气在头部区域速度很低。弹身压力很小较头部相差两个数量级。由密度分布可以清楚的看到在弹头和弹身流场的激波，且弹体的激波层的厚度尺寸与弹体的特征尺寸相比要小很多。

通过Fluent求解器获取到边界层外缘的气动热参数，将驻点区域边界层外缘参数代入Fay-Riddle驻点热流密度计算公式计算热流密度qws，非驻点区域代入平板热流密度公式求解平板热流密度qw。求得的热流密度与NASA对D-5450 的实验结果和纯数值对D-5450算法的纯数值计算进行对比，说明耦合算法的可行性。

坐标轴横坐标表示弹体上一点的特征尺寸与弹体特征长度的比值，纵坐标表示弹体的热流密度与实验驻点热流密度qws=2.65×105W/m2的比值。工程算法的驻点热流密度qws=356 328 W/m2，耦合算法求得的驻点热流密度qws=358 902 W/m2相对误差为0.007，说明所采用的方法与纯工程算法具有相同的精度，非驻点区域热流与实验值吻合较好。数据对比如图5所示。

图5 钝锥模型头部计算结果

3 带防热层的复杂外形弹箭的气动热研究

通过D-5450算例证明了可以较为精准的为气动热防护问题提供数值计算。本文研究对象为图6所示的复杂外形弹箭。

上述的压力和密度云图可以清晰地捕捉到脱体激波，压强和密峰值出现在头部。根据这些现象，说明本文的数值算法求解边界层外缘参数基本符合物理解。将边界层外缘参数导入到本文的工程计算方法得到弹体表面的热流密度分布如图8所示。

图6 弹体与对称面网格

弹体在初始时刻热流密度最大值和最小值分别为1.4×106W/m2、16 923 W/m2，弹体在50 s时热流密度最大值和最小值分别为3×105W/m2、12 697 W/m2。在弹体表面的热流密度和弹体最内层热流密度确定后，边界条件得到确定，可以进行平板的非稳态导热求解。基于非稳态导热微分方程可求得经过一次时间步长后弹体的温度分布。再将最外层表面温度代入平板热流密度公式，求得新的热流密度，再代入导热方程进行温度求解，以此类推进行循环。每次循环时间为一个时间步长，当时间步长满足迭代条件时可以输出弹体温度分布结果。

图7 弹体密度与压力云图

图8 弹体表面热流密度

本文选用3种材料作为三层防热层的涂层，由外至内分别为防热层1、主防热层2、防热层3，厚度分别为5 mm、20 mm、5 mm。本文提出不同的方案研究防热层的温度，在长航情况下监测不同时刻防热层不同位置的温度T1、T2、T3、T4(T1、T2、T3、T4分别为最外层的点、第一层与第二层交界点、第二层与第三层交界点、最内层点)。

本文的防热层材料的物性参数如表1所示。

表1 防热层物性参数

方案1：SiC、C/SiC、Al2O3分别为防热层1、主防热层2、防热层3。经过计算后的各个时刻不同点的温度分布如图9所示。

在方案1中共有4个不同时刻的防热层不同监测点的温度分布，可以看出随着飞行时间的增加，最外层温度T1在20 s很快上升至1 000 K且在后续的飞行过程温度提升很小，而防热层内部温度T2、T3、T4分布呈现线性增长的趋势。说明了热流是由外往内传递，且最外层的气动加热很快趋于最大值，内部的温升主要是由防热层的热传导决定。

方案2：Al2O3、C/SiC、SiC分别为防热层1、主防热层2、防热层3。经过计算后的各个时刻温度分布如图10所示。

方案2是将方案1的第一层与第三层进行交换，材料的选择和厚度与方案1保持一致。SiC的导热系数为Al2O3的3.5倍，由方案2的温度分布可以看出同热流密度情况下，导热系数越大温差越小。因此同热流密度下最外层材料的导热系数越大，T1的温度越低。

方案3：Al2O3、3Al2O3·2SiO2、SiC分别为防热层1、主防热层2、防热层3。经过计算后的各个时刻温度分布如图11所示。

在方案3中将主防热层2采用为比C/SiC热扩散率更大的3Al2O3·2SiO2。由方案3各个时刻温度分布可以看出同一时间差情况下，热扩散率α越大防热层节点温度越高，即热扩散率越大下一时刻的节点温升越大。通过方案3与方案2的对比，方案3在50 s长航状况下最内层T4的最大值比方案2的最大值要高90 K，说明了热扩散率越大节点温升越高。

方案4： SiC、3Al2O3·2SiO2、Al2O3分别为防热层1、主防热层2、防热层3。经过计算后的各个时刻温度分布如图12所示。

经过4种方案的对比，本文给出了防热层的温度分布的两个主要影响因素：最外层的导热系数和主防热层的热扩散率。最外层的导热系数越大防热层的热防护效果越好，最外层温升越慢。主防热层的热扩散率越大防热层的热防护效果越差，整个防热层的温升越快。

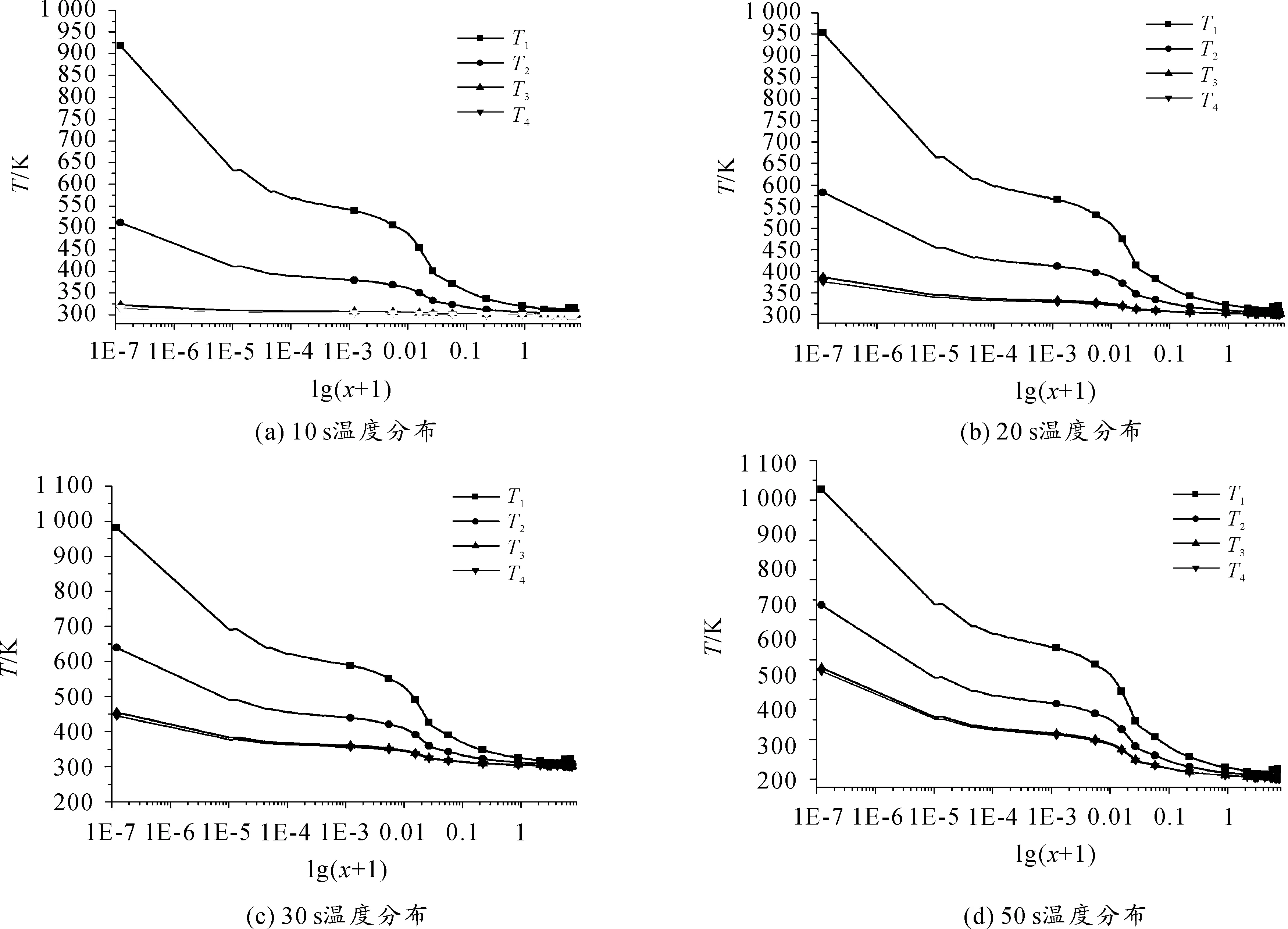
图9 方案1温度分布

图10 方案2温度分布

图11 方案3温度分布

图12 方案4温度分布

4 结论

本文采用耦合算法对D-5450钝锥算例进行了验证，在验证了算法的准确性后，对复杂外形火箭弹的防热层温度分布进行了研究，给出了物性参数对温度分布的影响。得出的主要研究结论有如下几点：

1) 同一时刻下，通过防热层最内层与最外层的温度对比，说明了火箭弹在添加防热层后能有效地延缓热量向火箭弹传递，降低了火箭弹的温度，保护火箭弹不受高温影响。

2) 通过选取不同的材料，研究防热层的温度分布，得出了防热层物性参数对弹体气动加热的影响规律，即：最外层导热系数越大，防热层防热效率越高，温度越低；主防热层热扩散系数越低，防热层防热效率越高，温度越低。

本文对于防热层的气动热分析仅仅进行了零功角的分析，未考虑高超声速火箭弹的复杂飞行状况，因此在后续开展的工作中将研究不同功角下火箭弹的防热层气动加热。

[1] 王国雄.弹头技术(上)[M].北京：中国宇航出版社，2005.

[2] 李惠峰，余光学.近空间高速飞行器多模型最优控制器设计[J].Proceedings of the 31stChinese Control Conference,2012：864-869.

[3] 姜贵庆，刘连元.高速气流传热与烧蚀热防护[M].北京：国防工业出版社，2003.

[4] 张志成.高超声速气动热和热防护[M].北京：国防工业出版社，2003.

[5] 李惠峰.高超声速飞行器制导与控制技术(上)[M].北京：中国宇航出版社，2012.

[6] 钱翼稷.空气动力学[M].北京：北京航空航天大学出版社，2004.

[7] FRED R.DEJARNETTE.A Review of some Approximate Methods Used in Aerodynamic Heating Analyses[J].Journal of Thermophysics and Heat Transfer,1985,1(1):5-12.[8] JOHN D.ANDERSON,JR.Hypersonic and high temperature gas dynamics[M].USA:McGraw-Hill BookCompany,1989.

[9] 吕红庆.高超声速钝头体气动热分析[J].导弹与航天运载技术,2008,295(3):41-45.

[10]杨光达.基于轴对称比拟的高超声速复杂外形气动热预测方法研究[J].航空计算技术,2014,44(2):95-101.

[11]雷延花.高超音速飞行器气动加热计算[J].上海航天,2001,18(5):10-13.

[12]邹小飞.再入弹头气动加热及热响应分析[D].长沙：国防科技大学,2009.

[13]马继魁.高超声速钝头体表面热流的数值模拟[J].科学技术与工程,2010,10(36):9019-9022.

[14]梁强,张平峰.基于CFD复杂外形飞行器气动加热高效算法[J].上海航天,2013,30(5):14-20.

[15]陈鹏.高速弹头气动热工程算法与数值计算研究[D].南京：南京理工大学,2013.

[16]张志豪， 孙得川.飞行器气动加热烧蚀工程计算[J].兵工学报，2015(12):1949-1954.

(责任编辑 周江川)

Research on Different Plan of Heat Shield Impacting on Aerodynamic Heating

ZHOU Yu-hang, ZHANG Xiang-hong, ZHANG Min

(School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

This paper calculated thermal parameters of rocket using aerothermal calculation coupling engineering and numerical algorithms with hypersonic rocket. Inviscid numerical algorithm was adopted to obtain parameters of the outer edge of the boundary layer while engineering algorithm was used in the inner area of the boundary layer where the viscosity plays a leading role. Since the size of the thickness of the heat protection layer is much smaller than the one of the surface of the rocket, the aerodynamic thermal calculations of heat shield were simplified one-dimensionally in this paper which establishes differential equation of one-dimensional unsteady heat conduction. The temperature distribution of heat protection of rocket layer under the state long-endurance was obtained through solving differential equation of heat conduction. Physical parameters of the heat shield impacting on the aerodynamic heating were obtained through the study of regular pattern of the physical parameters of heat protection layer, which provides a reference for the study of aerothermal protection.

heat shield; numerical algorithm; engineering algorithm; hypersonic; aerothermal parameter

2016-06-11；

2016-07-09

十二五总装预研项目

周宇航(1996—), 男, 硕士研究生, 主要从事气动加热方面研究。

10.11809/scbgxb2016.10.005

周宇航，张向洪，张敏.高速火箭弹不同防热方案对气动加热影响规律的研究[J].兵器装备工程学报，2016(10):24-30.

format:ZHOU Yu-hang, ZHANG Xiang-hong, ZHANG Min.Research on Different Plan of Heat Shield Impacting on Aerodynamic Heating[J].Journal of Ordnance Equipment Engineering,2016(10):24-30.

TJ415

A

2096-2304(2016)10-0024-08