引信后坐保险机构斜置设计方案

刘 宣，闻 泉，王雨时，张志彪

(南京理工大学机械工程学院，江苏 南京 210094)



引信后坐保险机构斜置设计方案

刘 宣，闻 泉，王雨时，张志彪

(南京理工大学机械工程学院，江苏 南京 210094)

针对引信后坐保险机构安全和可靠解除保险之间的矛盾，提出了引信后坐保险机构斜置设计方案。该方案是将传统的轴线与引信轴线平行或重合的后坐保险机构相对于引信轴线斜置一定角度设置。应用刚体动力学理论分析了引信后坐保险机构斜置设计动态特性，并给出了算例。仿真验证结果表明：后坐保险机构斜置设计有助于提高勤务处理弹丸和引信意外跌落时引信安全性，即有助于提高引信防止意外解除保险的性能，而正常解除保险性能不会受到影响。

引信；后坐保险机构；安全性

0 引言

保险机构是引信的重要组成部分，用来保证发火机构、隔爆机构及其他机构在勤务处理过程中处于保险状态，而只有在发射或其他预定条件下才能解除保险，使引信处于待发状态。

引信后坐保险机构作为惯性保险机构的一种，其应用最为普遍。文献[1]分析了引信后坐机构勤务处理安全性计算公式，介绍了最大响应计算方法，并进一步研究了机构运动特性；文献[2]介绍了引信单行程保险机构运动特性及保险机构惯性件速度响应计算方法；文献[3]研究了引信经典后坐保险机构对过载时间的响应特性，得到了不同后坐过载曲线下引信经典弹性后坐保险机构和刚性后坐保险机构解除保险响应特性；文献[4]介绍了引信后坐保险机构设计的冲击响应方法，使后坐保险机构的分析与设计更加高效；文献[5]利用Working Model 3D软件对引信双自由度后坐保险机构进行计算机仿真计算，并结合具体实例进行了结构优化设计；文献[6]研究了引信双自由度后坐保险机构动态响应特性，运用分段求解耦合微分方程组的方法得出机构位移响应。

以上文献只是针对引信后坐保险机构运动特性进行了理论分析或仿真研究，并未对低后坐过载条件下引信后坐保险机构安全和可靠解除保险之间的矛盾进行讨论。针对此问题，诞生了各种阻尼式后坐保险机构，如曲折槽后坐保险机构、双自由度后坐保险机构等。本文基于弹丸和引信跌落冲击的方位特性，即弹丸和引信倾斜跌落时的冲击远低于垂直跌落时冲击的事实，提出引信经典后坐保险机构斜置设计方案。

1 弹丸跌落冲击响应特性

引信后坐保险机构的安全性设计一直是分析研究的重点与难点，机构的设计必须满足：在装卸、运输、储存和跌落等勤务处理过程中处于安全状态；使弹药在目标或目标区正常引爆时必需能够可靠解除保险。通常，设计者都是利用弹丸在发射时产生的后坐力作用时间较长，而勤务处理时偶然跌落产生的冲击力作用时间较短这一特性[7]，来解决引信后坐保险机构安全和可靠解除保险之间的矛盾。

弹丸发生意外跌落的姿态是不确定的，且不同的跌落姿态会对弹丸的冲击特性产生影响。文献[8]对不同跌落姿态下弹丸冲击特性进行了研究，结果表明垂直跌落时加速度峰值比倾斜30°(弹丸轴线与竖直线的夹角)跌落时增大45%，比倾斜60°跌落时增大79%；文献[9]采用数值模拟方法研究子弹药以不同落角撞击混凝土介质的冲击响应，结果表明垂直跌落时加速度峰值比倾斜15°跌落时增大35%，比倾斜30°跌落时增大55%。上述文献跌落冲击结果存在差异的主要原因是选取的仿真结构模型和材料模型不同，但都表明垂直跌落对弹丸的冲击影响最大。

事实上，在垂直跌落时，弹丸或引信底部触碰跌落目标部分强度和刚度最大，全部动能均由弹丸或引信底部承受，因而形成的冲击过载最大，对引信后坐保险机构的冲击影响也最大。而在非垂直跌落时，弹丸或引信底部触碰跌落目标部分只是局部，强度和刚度较低，形成的冲击过载较小。

2 引信后坐保险机构斜置设计原理

2.1 构建物理模型

引信斜置后坐保险机构是将传统的轴线与引信轴线平行或重合的后坐保险机构相对于引信轴线斜置一定角度α设置，如图1所示。该机构由保险件(惯性体1)、被保险件(钢珠2)、本体3和抗力件(惯性簧4)组成，其中α为斜置角度。发射或跌落时，惯性体受后坐惯性力作用，下沉到一定距离，其中跌落时该距离不足以释放被保险件(钢珠2)，而发射时该距离要足以释放被保险件(钢珠2)，从而解除保险。

2.2 构建数学模型

如图1所示的引信斜置后坐保险机构：在机构处于保险状态情况下，惯性簧有一定的预压量，其抗力作用于惯性筒，且惯性筒在引信体的反作用力及摩擦力的作用下，处于平衡状态；在机构处于发射或跌落状态下，后坐惯性力开始作用于惯性筒，随着后坐力的增大，惯性筒开始运动并逐渐解除保险。根据后坐保险机构运动特性，得到质量块受力特性，如图2所示，其中F1是引信体对惯性筒的反作用力、F是惯性簧对惯性筒的弹性抗力、FN是惯性筒驻室侧壁对惯性筒的挤压作用力、Ff是惯性筒受到驻室侧壁的摩擦力、FS是引信后坐惯性力。

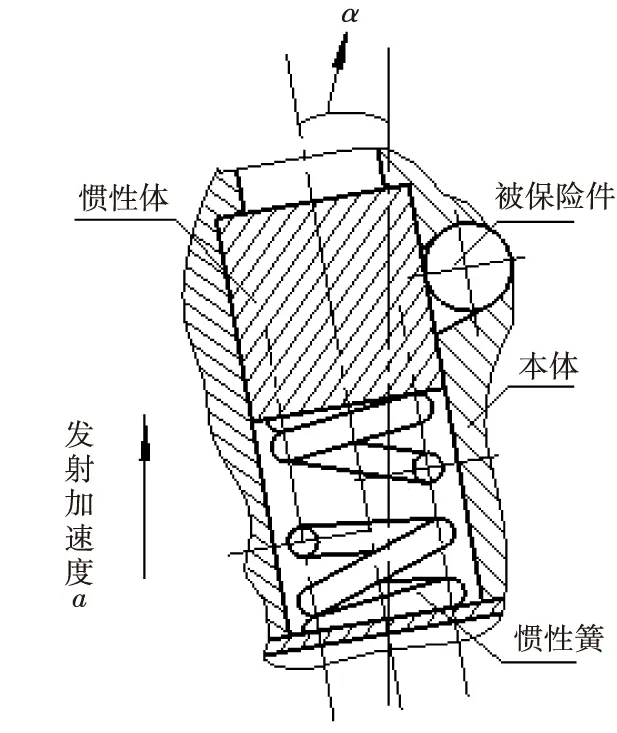
图1 引信斜置后坐保险机构Fig.1 Inclined design of Fuze Setback Arming Device

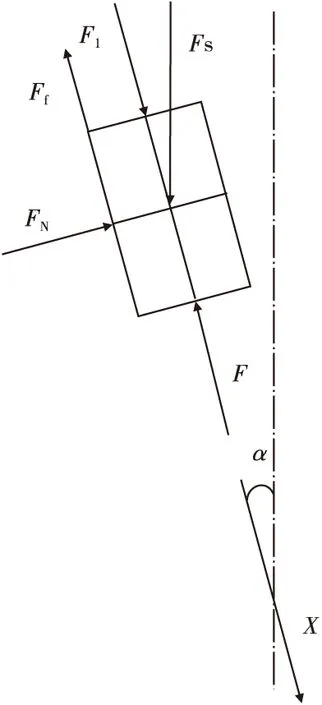
图2 质量块受力特性Fig.2 Mass mechanical characteristics

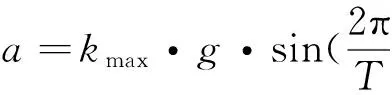
将质量块的运动过程分为两个阶段：把发射或跌落开始的时间到质量块开始运动的时间(记为临界值点t0)作为第一阶段；把临界值点t0到后坐过载(或跌落冲击过载)作用结束的时间作为第二阶段。分析惯性筒运动特性可知：

1)第一阶段(0≤t≤t0)

(1)

2)第二阶段(t0≤t≤T/2)

(2)

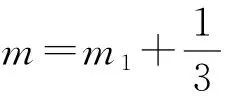
由式(2)可得惯性筒运动微分方程：

(3)

对式(3)求解得到：

(4)

将t=t0时，x=0,x′=0的初始条件代入公式(4)求出C1和C2：

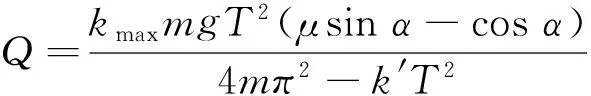
将C1和C2代入式(4)进一步化简，得

由质量块受力特性以及式(1)至式(4)可知：

1) 在已知机构设计参数的条件下，kmax、T、α是决定引信后坐保险机构解除保险作用时间的关键因素：随着kmax、T的增大，引信后坐保险机构更易于解除保险；随着α的增加，引信后坐保险机构更不易于解除保险。

2) 引信后坐保险机构斜置设计质量块开始运动的必要条件是：

kmaxmg(cosα-μsinα)sin(2πt/T)-k′λ≥0。

3) 由于斜置角度α的引入以及摩擦因素的存在，引信后坐保险机构斜置设计可靠解除保险即质量块沿着斜面运动而不发生自锁的必要条件是：

α<90°-arctan u。

2.3 算例分析

选用两组机构设计参数对引信后坐保险机构斜置设计动态特性进行数值分析和仿真比较研究，两组机构设计参数分别来源于不同的文献，如表1所列。摩擦系数μ取为0.15。

表1 机构设计参数

设计初期一般可以估取无包装的裸露弹药1.5 m高度垂直跌落到铸铁板或钢板时引信内部零部件所受到的冲击过载最大量值为7 000～15 000g，作用时间约为150～250 μs。本文取最大冲击过载系数kmax=10 000，作用时间t=100 μs对后坐保险机构进行跌落计算，得到两组设计参数在不同斜置角度α下对应的惯性体位移与作用时间关系，如图3所示。

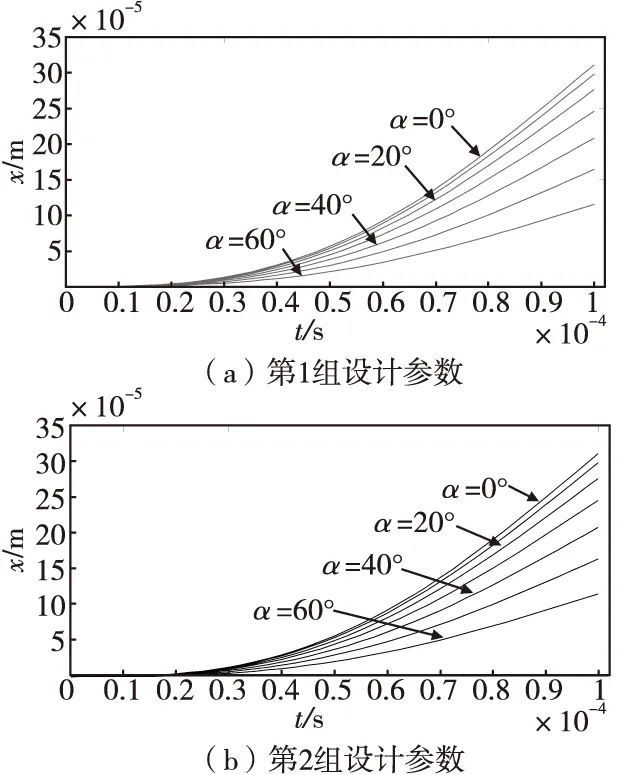
图3 跌落冲击作用下不同斜置角度α对应的惯性体位移与作用时间关系Fig.3 Correspondence between displacement and time of inertial body under drop impact

利用表1中的两组机构设计参数，最大后坐过载kmax=10 000，作用时间t=1.2 ms对后坐保险机构进行发射计算，得到两组设计参数在不同斜置角度α下对应的惯性体位移与作用时间关系，如图4所示。

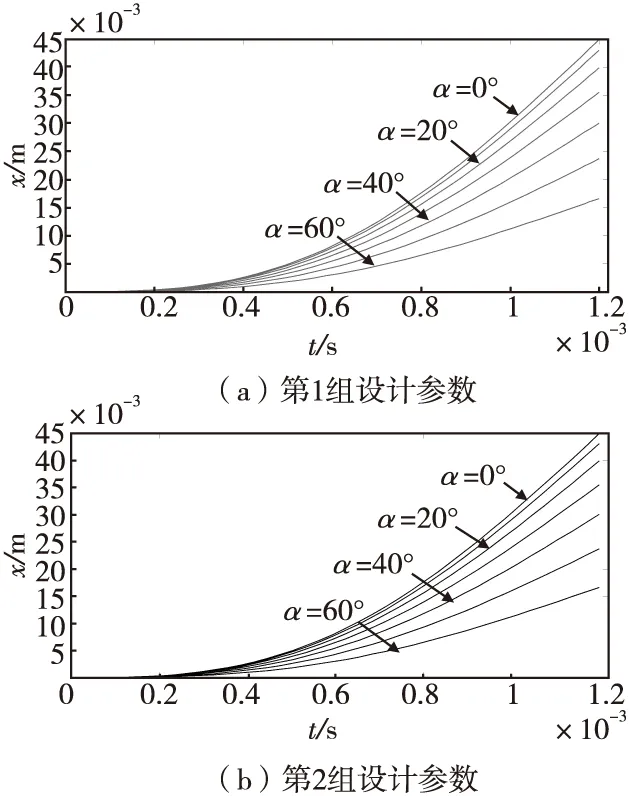
图4 发射后坐过载作用下不同斜置角度α对应的惯性体位移与作用时间关系Fig.4 Correspondence between displacement and time of inertial body under emission overload effect

由图3和图4可看出，斜置角度α对引信后坐保险机构运动特性有显著影响：无论是跌落冲击作用还是发射后坐过载作用，不同斜置角度α对应的x-t曲线数值上都有明显的差异；随着α的增加，相同作用时间下惯性体的位移明显减小。

3 仿真验证结果分析

为进一步探究斜置角度α对引信后坐保险机构安全和解除保险性能的影响，验证理论分析的正确性，运用ADAMS软件对后坐保险机构斜置运动特性进行仿真分析，同样取表1的机构设计参数作为仿真参数，且过载系数kmax、作用时间t与理论分析时相同。建立仿真简化模型，该模型由斜置侧壁，运动质量块，柔性体弹簧组成，如图5所示。设置质量块、斜置侧壁材料属性，赋予其质量特性；设置弹簧属性，给k′、λ 赋值；给运动质量块添加移动副，并在移动副上设置摩擦特性(μ取为0.15)；给运动质量块施加后坐力(或跌落冲击力)FS；定义运动质量块与斜置侧壁间的接触。

图5 仿真模型Fig.5 Simulation model

由于2组机构参数相差较小且从得到的结果来看，无论是仿真值还是理论值两组设计参数对应的结果数值非常接近，所以在此只对表1中的第1组设计参数得到的数值结果列表分析：得到发射后坐过载作用下不同斜置角度α对应的解除保险作用时间(表2)；由于在跌落冲击作用下本算例中后坐保险机构不足以解除保险，但为了直观地分析斜置角度α对引信后坐保险机构的影响，表3列出了不同斜置角度α对应的冲击过载作用时间t=100 μs时惯性筒的位移。

在发射后坐过载或跌落冲击作用一定的条件下，分析表2和表3数据可得：

1) 理论结果与仿真结果比较接近，证明了理论分析的可信性。ADAMS软件无法赋予弹簧质量特性，经验证弹簧质量对结果的影响比较小，误差在0.5%以内；摩擦系数μ可能是影响误差的主要因素，验证表明摩擦系数μ值减小，总体平均误差值也减小，但幅度并不明显。

2) 引信后坐保险机构斜置设计有助于提高其安全性，即有助于提高防止意外解除保险的性能，而正常解除保险性能一般不会受到影响。

表2 发射后坐过载作用下不同斜置角度α对应的解除保险作用时间

表3 跌落冲击作用下不同斜置角度α对应的t=100 μs时惯性筒位移

4 结论

本文提出了引信后坐保险机构斜置设计方案，该方案是将传统的轴线与引信轴线平行或重合的后坐保险机构相对于引信轴线斜置一定角度α设置，应用刚体动力学理论进行了理论分析并应用ADAMS软件仿真研究了发射和跌落时引信后坐保险机构斜置设计动态特性。仿真验证结果表明：引信后坐保险机构斜置设计有助于防止意外解除保险，而正常解除保险则不会受影响；引信后坐保险机构斜置设计提高了勤务处理弹丸和引信意外跌落时的引信安全性，有利于解决引信后坐保险机构安全和可靠解除保险之间的矛盾。

[1]李世义.后坐机构平时安全性研究[J]. 兵工学报，1983(2):50-63.

[2]GJB/Z 135-2002.引信工程设计手册[S]. 北京：中国人民解放军总装备, 2002.

[3]李来福，王雨时，闻泉.引信经典后坐保险机构对过载时间的响应特性[J].四川兵工学报， 2014(7)：147-152.

[4]陈庆生. 冲击振动理论与应用 [M]. 北京：国防工业出版社, 1989.

[5]秦文.双自由度后坐保险机构的计算机动态仿真[J].探测与控制学报，2003，25(1)：57-59.

[6]曹莹，王雨时. 引信双自由度后坐保险机构动态响应特性分析 [J]. 探测与控制学报，2008,30(2):47-50.

[7]《引信设计手册》编写组.引信设计手册[S]. 北京:国防工业出版社，1978.

[8]邦志辉. 水声对抗子母弹结构冲击响应研究[D]. 南京: 南京理工大学,2014.

[9]南宇翔，蒋建伟，王树有，等.子弹药落地冲击响应数值模拟及实验验证[J].振动与冲击， 2013(3)：182-187.

[10]严慎武. 新型制导炮弹安全与解除保险装置设计研究 [D]. 南京: 南京理工大学,2012.

Inclined Design of Fuze Setback Arming Device

LIU Xuan，WEN Quan，WANG Yushi，ZHANG Zhibiao

(Mechanical Engineering school, NUST, Nanjing 210094, China)

For the contradiction between safety and reliability of fuze setback arming device, the inclined design of fuze setback arming device was put forward.The program made the fuze axis inclined some degrees to the fuze axis. Dynamic characteristics of inclined design of fuze setback arming device was analyzed by rigid body dynamics theory.The results showed that the inclined design of fuze setback arming device contributes to improve the fuze safety when the projectile and fuze fall accidentally, and the performance of normal arming was not affected.

fuze；setback arming device；inclined design；safety

2015-12-15

刘宣(1989—)，男，山东济宁人，硕士研究生，研究方向：引信系统分析和机构动力学。E-mail:15564864028@163.com。

TJ43

A

1008-1194(2016)05-0010-05