基于蒙特卡洛法的关节臂坐标测量机工作空间分析

王学影，王 华，陆 艺，郭 斌

(中国计量学院 计量测试工程学院，杭州 310018)



基于蒙特卡洛法的关节臂坐标测量机工作空间分析

王学影，王 华，陆 艺，郭 斌

(中国计量学院 计量测试工程学院，杭州 310018)

传统的求解关节臂式坐标测量机工作空间的方法需要借助繁琐的数学公式、计算量大，针对这一问题选用蒙特卡洛法对工作空间进行分析；首先运用D-H方法建立关节臂式坐标测量机的数学模型得出运动学方程;然后采用蒙特卡洛法分析该测量机的工作空间，得出工作空间点云图；最后，采用局部象限分布的方法对关节臂式坐标测量机工作空间点云图的边界点进行提取;仿真实验结果表明用蒙特卡洛法对工作空间分析更简单易于实现，采用基于局部象限分布法提取到的边界点轮廓也更准确避免了虚假边界点的提取。

关节臂式坐标测量机；运动学模型；工作空间；蒙特卡洛法；边界提取

0 引言

关节臂式坐标测量机是一种新型的非笛卡尔式坐标测量系统[1]。该系统将一系列杆件通过具有旋转功能的关节连接起来，以角度测量取代了长度测量，具有机械结构简单，测量范围大，体积小，可便携等优点。因此在现代工业生产中对关节臂式坐标测量机的应用越来越广泛。测量机的关节数目、关节配置情况和结构尺寸等因素都会影响测量机的运动范围[2]。为了使坐标测量机能满足人们的需求所以必须对其工作空间进行研究。目前，国内外对关节臂式坐标测量机工作空间的研究还比较少，基本停留在对工作空间点云图的绘制上。对工作空间点云图的绘制方法分为定步距打点法和基于蒙特卡洛法的工作空间绘制两种方法。前一种方法计算量大，公式复杂，而蒙特卡洛法很好的弥补了前一种方法的缺点，所以这里采用蒙特卡洛法来分析工作空间。工业机器人在这方向的研究比较深入，绘制出点云图后还进行了边界点的提取，主要的方法有栅格搜索法、极值搜索法、文本搜索法和逆解搜索法等[3]。栅格法的原理是将工作空间划分为多个正方形的网格，按照规定的判别条件来确定边界单元，再用单元内点集坐标的平均值表示边界点的坐标值[4]。极值法是将工作空间按列划分，在固定的一段宽度范围内找工作区域边界的极大极小值[5]，这两个极大极小值点即为工作空间的边界点。这几种边界提取的方法理论知识较为完整，但提取到的点也只能是近似的边界点。因此本文先通过对坐标测量机运动学模型的分析得出运动学方程，再对关节臂式坐标测量机的工作空间进行分析，最后利用基于局部象限分布的方法对工作空间边界点进行提取，获得边界点的轮廓。

1 关节臂式坐标测量机运动学模型的构建

运动学模型的构建是关节臂式坐标测量机工作空间分析的基础。工作空间需要用数学方程来确定，要得到这个方程就要在理解关节臂式坐标测量机测量原理的基础上，建立合理的数学模型。

1.1 关节臂式测量机测量原理

关节臂式坐标测量机是根据仿生学原理，模拟人的四肢和躯干运动而构成的。它由多个关节构成，测头端安装有测量探头，可由人牵引在物体表面滑动扫描[6]。机械臂的关节上装有角度传感器，可以实时测量关节的转动角度，根据臂长和各关节的转动角度计算出测量点的三维坐标。

1.2 关节臂式测量机系统的数学模型

关节臂式坐标测量机的运动学模型采用的建模方法是基于准球坐标系改进以后的D-H建模方法[7]。这种建模方法可以简化运动模型中包含的参数，其坐标示意图如图1。

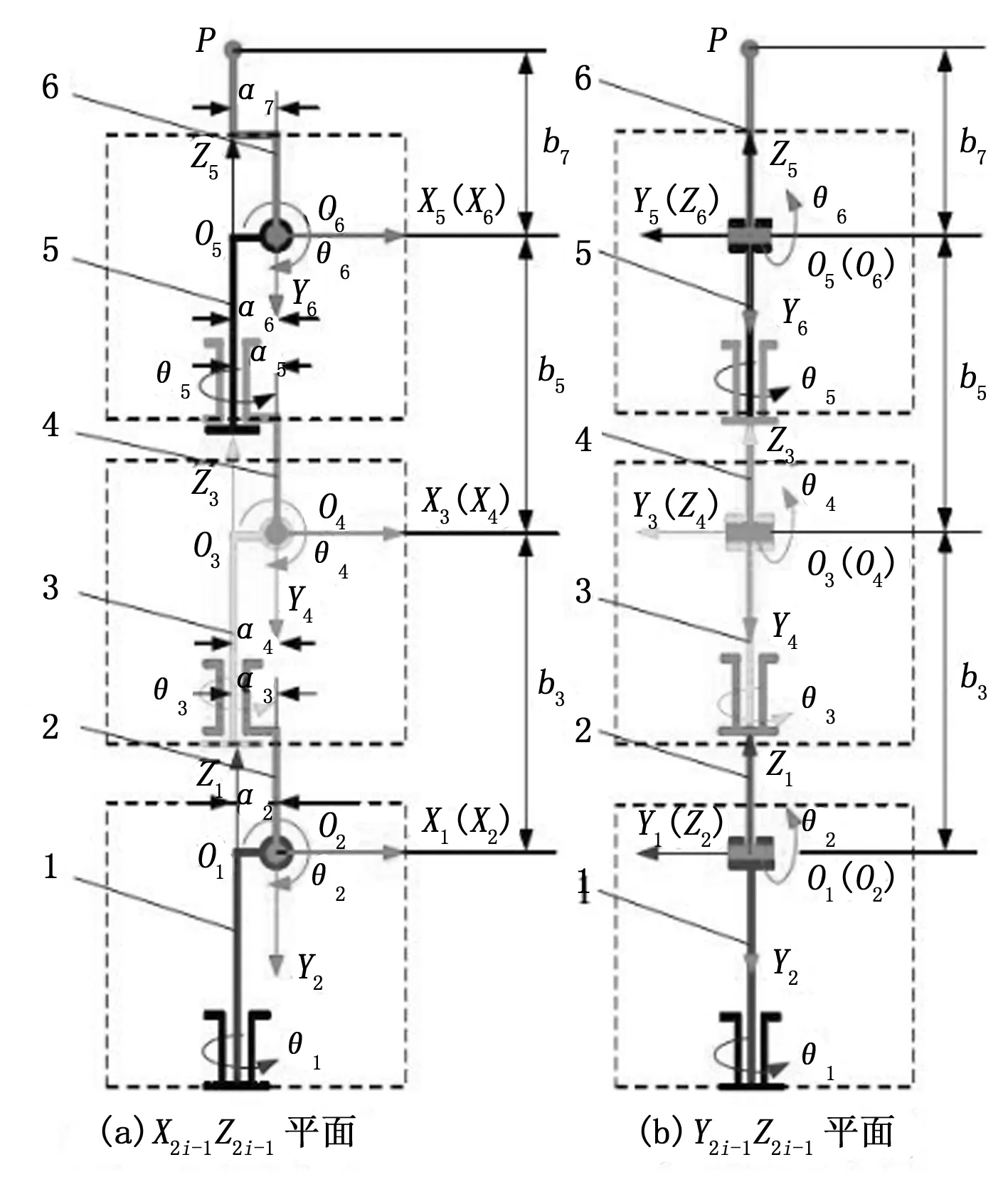
图1 测量机坐标系示意图

图1中的参数分别是关节转角θ1～θ6，测头端中心点在XYZ轴上的偏置分别为a1～a7、b1～b7、d1～d7以及每个关节的旋转中心O1～O6。

关节臂式坐标测量机是一种类似于工业机器人的多关节串联的开式运动链。运动学分析主要是研究柔性关节臂式坐标测量机各关节变量与其末端测头端的位置坐标之间的关系，是研究工作空间的基础。它们之间的关系可以由一个坐标变换矩阵表示[8]，坐标系{i}到坐标系{i+1}的变换关系如式(1)：

Ai,i+1=Rot(Zi,θi)Trans(Zi,di+1)Trans(Yi,bi+1)

(1)

由坐标变换矩阵可以得出关节臂式坐标测量机理想运动学方程模型如式(2)。

(2)

其中:(x67,y67,z67)是侧头点P在{O6X6Y6Z6}坐标系下的坐标值表达式，该表达式如下式(3)。

(3)

将公式(1)和(3)代入公式(2)得到最终测头点的位置坐标与关节转角之间关系的表达式如下式(4)。

(4)

式中，l1～l6中l=(lx，ly，lz)T表示第i个坐标系的X轴的方向相对于第i-1个坐标系的3个坐标轴的方向余弦。

2 测量空间分析

通过上面的分析，建立了合理的运动学模型得出了运动学方程，具备了进行测量空间分析的基本条件。但是由于关节转角在某个范围内是连续变化的，而运用蒙特卡洛法分析工作空间则是一种数字分析方法。我们需要定义工作空间的描述方法，将关节角度变量的取值与工作空间建立一种映射关系。然后再结合运动学方程完成对工作空间的分析。本文以海克斯康公司生产的Infinite2.0的测量机作为实验分析的对象。

2.1 工作空间描述

关节臂式坐标测量机的测量空间可定义为：测量机在正常工作时，测头端的中心点在整个空间所能测量的最大范围。在数学语言中，测量空间可以用测头中心点在不同关节相互组合运动的作用下所能达到的位置点的集合来表示[9]，即在三维空间R3中，该集合可视为关节变量与测量空间WF位置的映射，表示为下式(5)：

(5)

其中:θi为关节变量，i为关节数量；Ω为关节变量空间；T为关节变量与测量空间位置的映射关系。

2.2 工作空间分析

关节臂式坐标测量机工作空间的形状比较抽象无法直观想象，因此需要借助于数学工具来对它进行描述和分析。

关节臂式坐标测量机的各关节角度变量取值如表1所示。其中臂长的名义值分别为b3=285mm，b5=285mm，b7=220mm。

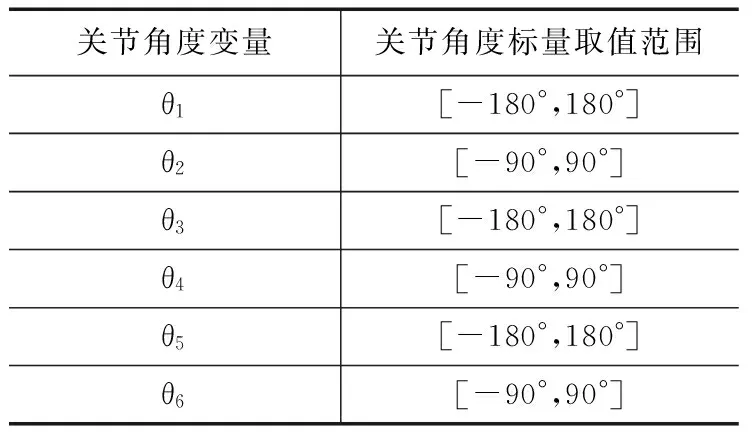
表1 关节角度变量的取值

用蒙特卡洛方法模拟关节臂式坐标测量机的工作空间，主要是利用运动学方程[10]。实质是利用蒙特卡洛技术对关节变量进行符合均匀分布的随机抽样，并将各关节变量的随机抽取的值代入运动学方程式(2)计算出关节臂测头中心点的坐标值，这些坐标值构成的集合即为关节臂的工作空间。

关节臂式坐标测量机的工作空间本来是一个连续分布的空间，而蒙特卡罗法是需要处理离散数据点，前面我们已经完成了符合这一算法的概率模型的构建[11]。然后要在各关节角度变化范围内利用均匀伪随机数RAND，逐个产生各关节变量，即：

式中，θi为第i个关节变量的随机值，θimin为第i个关节变量取值下限，θimax为第i个关节变量取值上限，各关节上下限的取值见表1。将上述过程产生的随机变量值带入运动学方程求出测头端中心点在基坐标系中各相应位置的坐标值，然后在软件中得出节臂式坐标测量机工作空间点云图如图2。

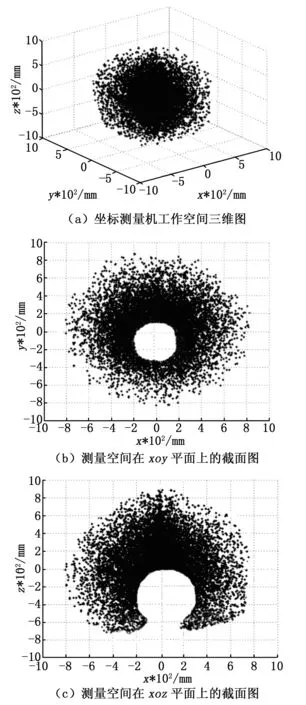
图2 工作空间点云图

从图2中的(a)图所示的测量机工作空间的三维图形可以看出，关节臂式坐标测量机的理想工作空间是一个完整的球体，可以测量自身参数允许范围内所有区域。图2中的(b)和(c)分别是图(a)在xoy和xoz平面上的投影图，从中可以看出在靠近坐标测量机的底座部分存在着测量机的不可触区域。最外层部位由于测量机的臂长和转角的约束，点分布相对稀疏，其它位置的点分布均匀，变化平缓，没有空心出现，这可以表明关节臂式坐标测量机结构的合理性。但是利用蒙特卡洛方法模拟获得的是测量机工作空间中一系列随机点的云图，为了更准确地分析工作空间的特性得到准确 的边界点坐标信息，我们还需要对点云图的边界点做进一步的分析[12]。

3 边界点提取方法

由于工作空间的点云图无法准确地表达出边界点的信息，因此对点云图边界提取的研究工作也很重要。本文采用的基于局部点象限分布的边界点提取方法的具体实现过程如下[13]。

该方法是以要判断点为原点，建立局部坐标系，通过分析边界点、内部点和邻域点的分布特点,发现如果该点为边界点,则4个象限至少有1个象限的点分布为空集。具体判别步骤如下:

1)搜索目标点i(xi,yi)的邻域点集合如式(6)：

(6)

其中:r为搜索半径；

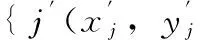
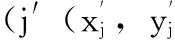
按照上述步骤逐点判断,即可找出所有的边界点。但是该方法需要搜索整个工作空间，计算量非常大，需要的时间较长。结合以往机器人工作空间分析中采用的按列划分的方法，将前面第一步中需要搜索的目标点的范围进行进一步的限定，具体做法流程图如图3。

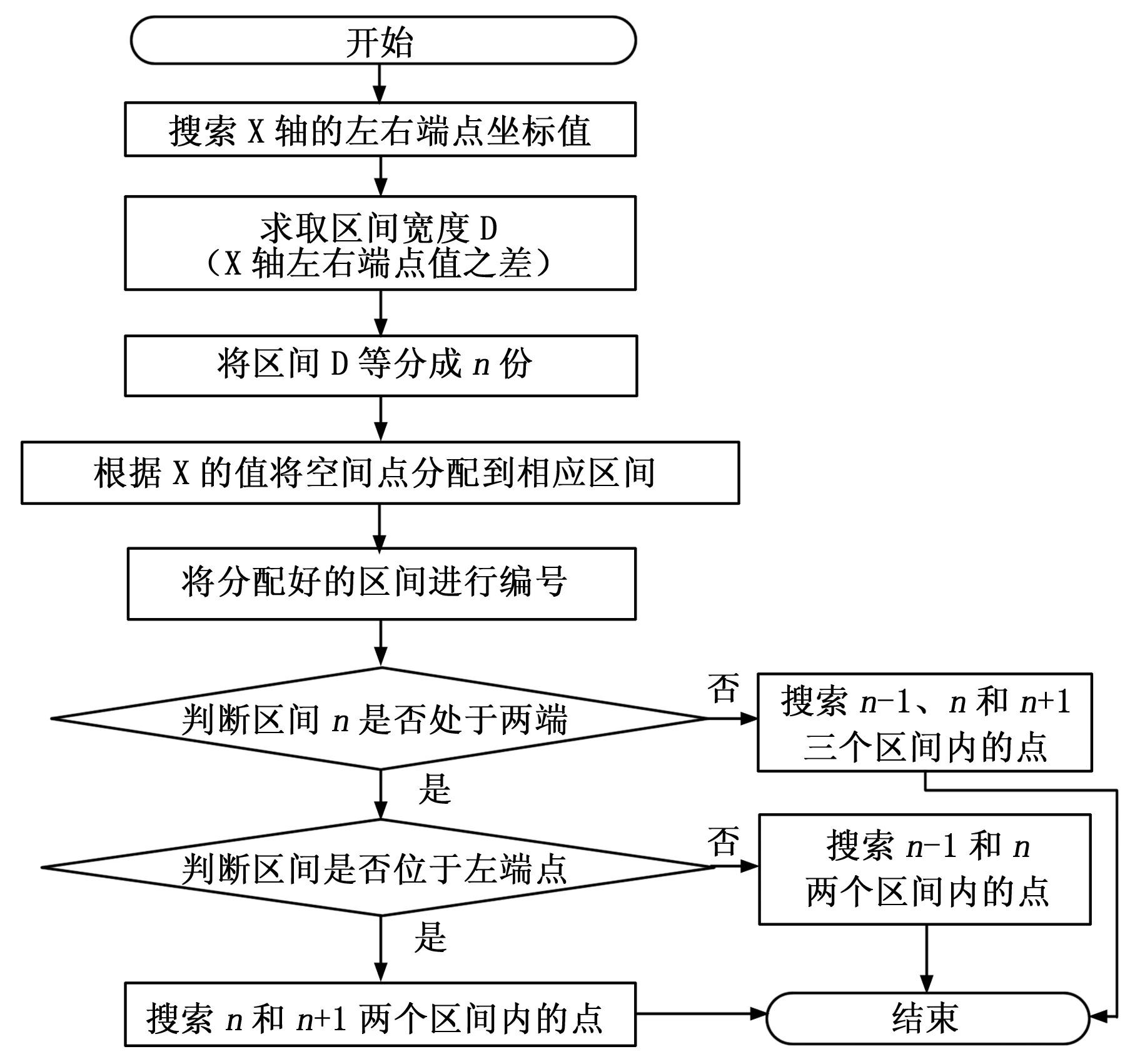
图3 边界点搜索流程图

4 试验结果与分析

采用本文的基于局部点象限分布法提取边界点的方法对实验室的海克斯康公司生产的Infinite2.0的关节臂式坐标测量机工作空间进行仿真试验。按照这种方法提取到的关节臂式坐标测量机工作空间边界点轮廓如图4。其中图4中的(a)是关节臂式坐标测量机在xoy平面内工作空间边界点的轮廓图，图(b)是关节臂式坐标测量机在xoz平面内工作空间边界点轮廓。用这种方法进行边界点提取时就不需要每次都对整个空间的工作点进行分析了，只需对不同的3个或者两个子区间的点进行分析即可得到较准确地边界点。从图中可以看到提取的边界点轮廓无虚假边界点，准确反映了工作空间边界信息。

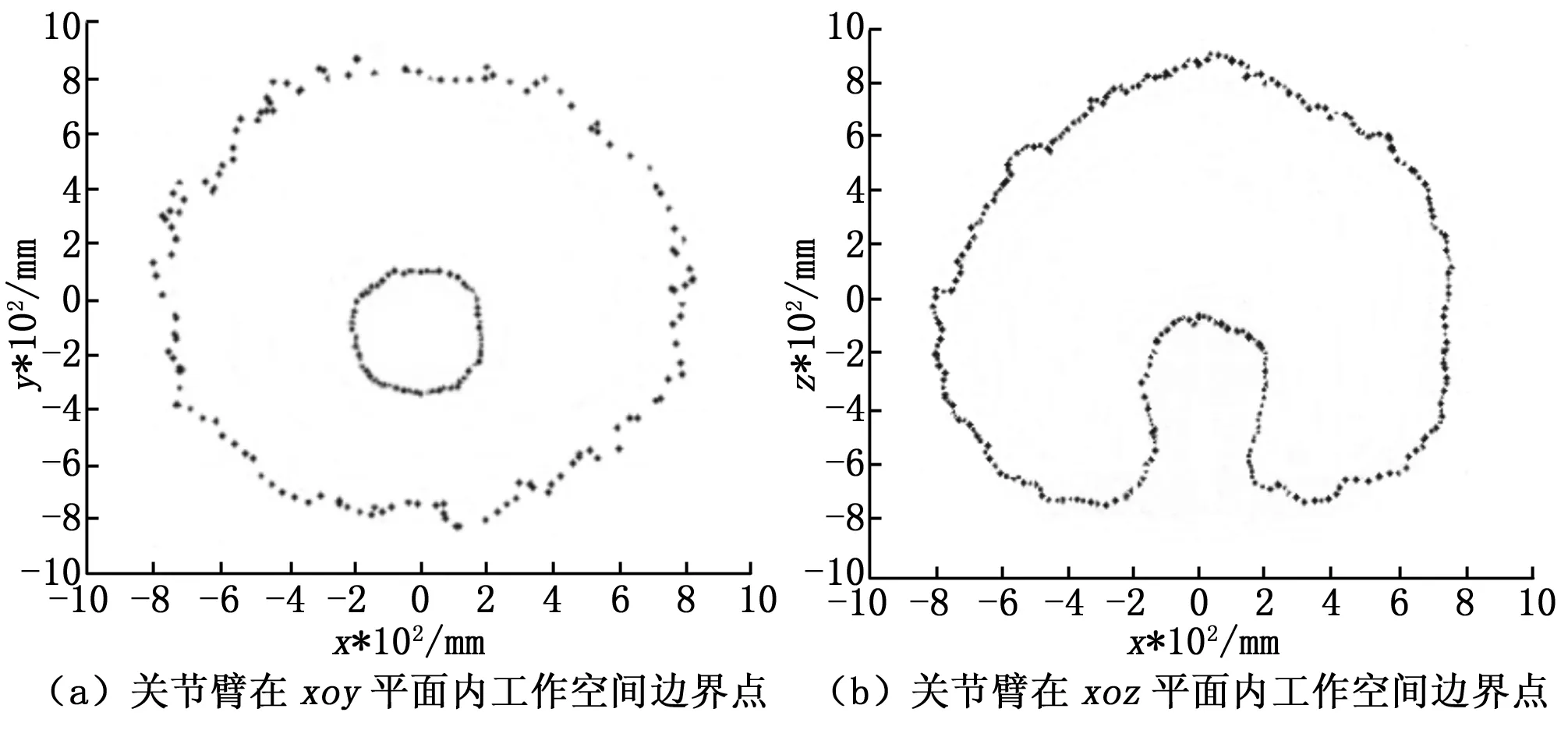
图4 关节臂坐标测量机工作空间边界轮廓

将图2工作空间点云图中(b)图测量空间在XOY平面上的截面图的局部进行放大分析得到如图5所示的结果。其中a、c和e三点为边界点，f、b、d和g是伪边界点。在该图中利用基于局部象限点分布法提取到的边界点是以图5中的a、c和e三点为代表的处于最外层的三点连线上的这一系列点，在包络线外没有漏掉的边界点，也没有提取到处于内部的伪边界点。

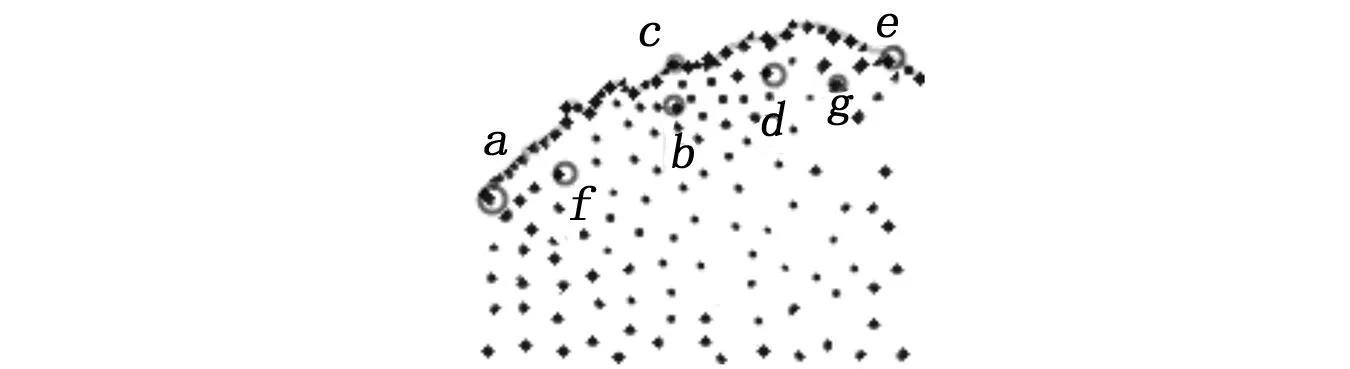
图5 测量空间XOY面上的局部放大图

相对于用极值法和栅格法提取边界点，本文的基于局部点象限分布法的提取精度更高，并且提取到的边界点更贴合与工作空间的实际边界，这种方法可以很好的避免虚假边界点的出现。

5 结束语

通过建立关节臂式坐标测量机的数学模型进而推导出了运动学方程，在此基础上用本文提到的方法对海克斯康公司生产的Infinite2.0关节臂式坐标测量机工作空间做了仿真分析绘制出了工作空间点云图并对其工作空间点云图进行边界点的提取。实验结果表明：用蒙特卡洛法分析绘制测量机的工作空间更简单，生成的工作空间点云图各点更贴近实际，可以由点云图中直观的看到关节臂的实际工作范围，便于人们合理的摆放测量机的位置。用基于局部点象限分布法能提取到测量机工作空间精确的边界点，对后续人们研究坐标测量机的最佳测量空间具有重要的意义。

[1] 裘祖荣，孙增玉，张国雄.关节臂式坐标测量机标定系统的设计[J].计算机测量与控制，2009,17(1):88-90.

[2] 郑大腾,肖忠跃,周燕辉. 提高关节臂式坐标测量机测量精度的关键技术[J]. 河北科技大学学报,2014,(1):20-23.

[3] 毛 新，罗庆生，韩宝玲,等.仿生六足爬行机器人运动控制技术研究[J].计算机测量与控制,2006,14(3):348-350.

[4] 刘志忠，柳洪义，罗 忠，等.机器人工作空间求解的蒙特卡洛法改进[J].农业机械学报，2013,44(1):230-235.

[5] 李保丰，孙汉旭，贾庆轩，等.基于蒙特卡洛法的空间机器人工作空间计算[J].航天器工程，2011,20(4):79-85.

[6] 田海波,马宏伟,魏 娟. 串联机器人机械臂工作空间与结构参数研究[J]. 农业机械学报,2013,44(4):196-201.

[7] 于连栋，程文涛，费业泰.基于激光跟踪仪的关节式坐标测量机参数标定[J].中国科学技术大学学报，2009,39(12):1329-1332.

[8] 王学影，刘书桂，王 斌，等.关节臂式柔性三坐标测量系统的数学模型及误差分析[J].纳米技术与精密工程，2005,3(4)：262-267.

[9] 田海波,马宏伟,魏 娟. 串联机器人机械臂工作空间与结构参数研究[J]. 农业机械学报,2013,44(4):196-201.

[10] 徐钟济.蒙特卡洛方法[M].上海：上海科学技术出版社，1985,6.

[11] 蔡 蒂，谢存禧，张铁邹，等.基于蒙特卡洛法的喷涂机器人工作空间分析及仿真[J].机械设计与制造，2009,(3):161-162.

[12] 吴学明，李灿平.边缘检测算法在不同分辨率图像中的性能研究[J].计算机测量与控制，2006,14(2):166-169.

[13] 陈是扦,刁 燕,罗 华,等.机器人工作空间边界点提取算法研究与改进[J].机械传动,2014,(11):49-53.

Workspace Analysis of Articulated Arm Coordinate Measuring Machine Based on Monte Carlo Method

Wang Xueying，Wang Hua，Lu Yi，Guo Bin

(Institute of Precision Measurement and Control, China Jiliang University,Hangzhou 310018,China)

The traditional method to solve the problem of working space of articulated arm coordinate measuring machine needs applying complex mathematical formulas with large calculating quantities. To solve this problem, the Monte Carlo method was used to analyze the working space.Firstly, the D-H method was used to establish the mathematical model of coordinate measuring in order to obtain the Kinematics equations.Then, the Monte Carlo method was used to analyze the working space of the measuring machine in order to draw the cloud picture of the work space.Finally,we could extract the boundary points of the workingspace of the articulated arm coordinate measuring machine by using the method of the local quadrant distribution. The results of simulating experiments show that the Monte Carlo method is more simple and easier to operate on the analysis of space. The boundary points extracted by using the method of local quadrant distribution are more accurate avoiding the extraction of the false boundary points at the same time.

articulated arm coordinate measuring machine;kinematic model;workspace; Monte Carlo method;boundary extraction

2015-11-17；

2015-12-18。

国家自然科学基金项目(51405463)。

王学影(1979-)，女，黑龙江大庆人，副教授，硕士研究生导师，主要从事光电检测技术、三坐标测量机技术方向的研究。

1671-4598(2016)06-0030-04

10.16526/j.cnki.11-4762/tp.2016.06.009

TH721

A