精密离心机动态半径测试方法研究与实现

周继昆，张 荣，张 毅，王 珏，凌明祥

(中国工程物理研究院 总体工程研究所，四川 绵阳 621999)



精密离心机动态半径测试方法研究与实现

周继昆，张 荣，张 毅，王 珏，凌明祥

(中国工程物理研究院 总体工程研究所，四川 绵阳 621999)

为了对精密离心机动态半径进行有效的测量，提出了一种基于外基准的定点定位测量方法，并利用电容测微仪、24位高精度PXI数据采集卡搭建了动态半径测试系统；在测试过程中，首先对离心机动态半径数据进行等角度采样，然后精确提取精密离心机定位平台所在的转盘外边缘的局部数据，再将不同转速下的局部数据进行点对点的比较，计算出动态半径；对测量结果的不确定度进行了评定，评定结果表明，文中提出的测试方法能够实现对精密离心机动态半径较高精度的测量，测量精度可达0.085 μm。

精密离心机；动态半径；PXI数采

0 引言

精密离心机动态半径是影响精密离心机输出加速度精度的一个重要分量，必须进行准确测量，并将其作为分量补偿到精密离心机加速度输出模型中，使精密离心机输出高精度的加速度信号[1]。精密离心机的动态半径的测量方法主要分内基准与外基准两类[2]。若使用内基准测量动态半径时，测量结果中未包含空气主轴的径向回转误差，因此需单独测试主轴径向回转误差，再将回转误差与转盘径向伸长量求和得到。而采用外基准测量时，测量结果中已包含主轴径向回转误差，因此不用将回转误差补偿到动态半径中。

在测量装置上一般采用双激光干涉仪[3-4]、差动位移传感器[5]、标准量杆和千分尺、电感测微仪和电容测微仪[2]。其中，有非接触测量、安装方便、动态频响较高的特点、适合动态测量和在线监测[6]。文献[7]采用两个电容测微仪对标称半径为3 000 mm的离心机动态半径进行测量，测量精度为0.33 μm；文献[8]采用电容测微仪对转臂式离心机的动态半径进行测量，测量精度为1 μm。上述文献在测量离心机动态半径时，并未对转盘形状误差等影响测量精度的进行考虑。为此，为了进一步提高动态半径的测量精度，提出一种基于外基准的定点定位测量方法，该方法首先对离心机动态半径数据进行等角度采用，然后精确提取精密离心机定位平台所在的转盘外边缘的局部数据，再将局部数据进行点对点的比较，计算出动态半径，消除了转盘外沿形状误差对测量精度的影响，且能够更为真实的反应加速度及安装处动态半径的变化。经过对测量结果的不确定度评定表明，测量精度可达0.085 μm。

1 外基准动态半径定点定位测量原理

1.1 精密离心机动态半径测量特点

外基准测量动态半径示意图如图1所示，利用电容测微仪直接对准精密离心机转盘边缘测试其径向半径变化量，对于理想的转盘，在不考虑转盘边缘的形状误差时，动态半径ΔR可由式(1)确定，其中R1与R2是在不同转速下电容测微仪测头到离心机转盘之间的距离。但在实际测量过程中，动态半径的测量精度会受到以下两个方面的影响。

(1)

1)当受机械加工能力限制，转盘的边缘无法做到精密加工，其形状误差通常为微米级误差，与动态半径在一个数量级，对于10-6量级的精密测量，不得不考虑转盘形状误差对动态半径测量的影响。因此，需采用一定的技术途径消除形状误差对测量结果的影响。

图1 动态半径测量示意图

2)由于被校加速度计安装在精密离心机的定位平台上，如图2所示。因此，取精密离心机定位平台所在的转盘外边缘的局部区域作为动态半径测试参考对象，在此方向上的动态半径才是定位平台处感受的最真实的半径变化，此方向的动态半径值对加速度计的标校更有实用价值。

为了解决上述两方面的问题，进一步提升动态半径测量精度，采用定点比较的方法消除转盘圆度误差对测量结果的影响，采用定位测量提高精密离心机的动态半径ΔR测量的真实性。

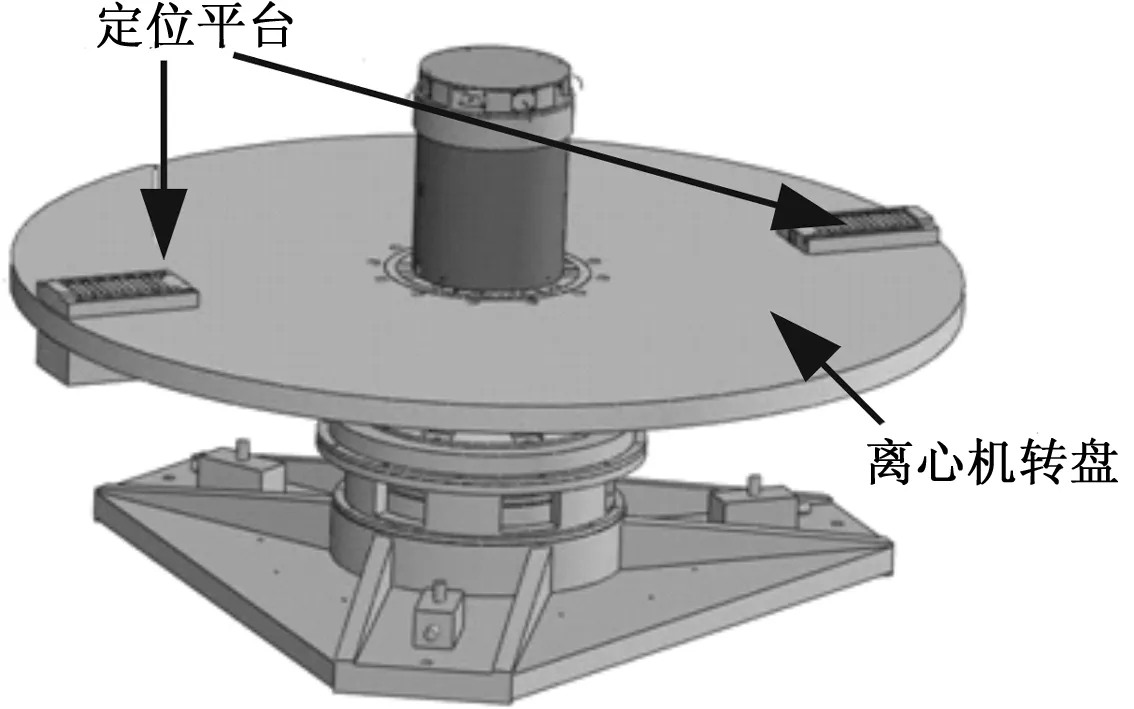
图2 定位平台安装示意图

1.2 动态半径定位原理

电容测微仪安装示意图如图3所示，主要利用电容测微仪在超量程时工作状态自动进入饱和区从而输出固定电压的特性来实现局部有效区定位。

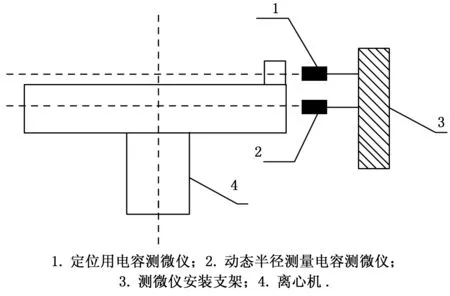
图3 电容测微仪安装示意图

离心机旋转时，定位用电容测微仪的输出信号示意图如图4所示。对两只电容测微仪输出进行同步同频率采样，即可分别获取离心机转盘动态半径数据和平台定位数据，然后根据定位平台的数据与转盘有效半径数据进行点对点对比即可得到动态半径测量数据中的有效数据段。

图4 定位用电容测微仪输出测试信号示意图

1.3 测试数据定点比对原理

在单次动态半径测试的原始测量值ΔRi(i=1,2，…，n)中包含有定位测试区域内n个测点的形状误差，为消除测点处形状误差对测量结果的影响，采用测点位置对齐测试法。该方法的主要思想是将转盘全周等角分为N个测点区域，在任何稳定的转速ω下，对转盘全周均只采集N个测点，只要高低g值下同一测点相对电容测微仪的测试区域是对齐的，则对高低g值下同一测点的两次测量信号相减，即可消除测点处的形状误差对测量结果的影响。

2 数据采集方案设计

数据采集方案示意图如图5所示。只有在对转盘不同的稳定转速下均等间隔采集N个测点，才可实现后续测点位置对齐信号相减消测点处形状误差的方案，为实现转盘每周采样测点位置严格对齐，利用精密离心机上的光栅编码器Z脉冲作为采样的触发的开始信号，以保证每次采样得到数据的初始相位一致。

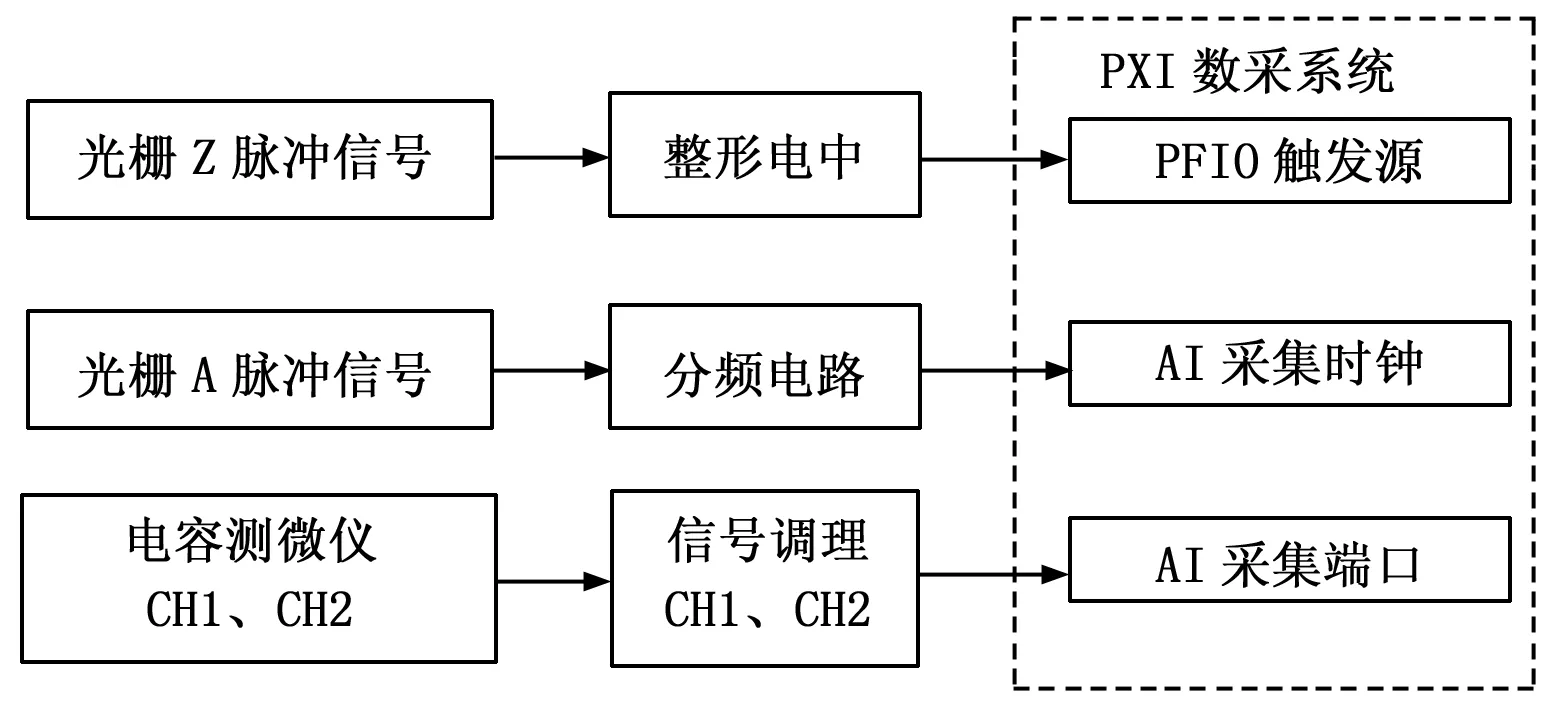
图5 数据采集硬件架构

利用A相脉冲的分频信号将转盘划分为等间隔的N个测试区域，N个测试区域产生N个测点，在转盘的任意稳定旋转角速度ω下，光栅编码器的A相脉冲频率跟随角速度ω自动变化，分频后保证每周只采集N个点。其中整型电路是将Z脉冲进行展宽，以便于PXI采集卡识别。

利用光栅编码器的A相脉冲信号经K次分频产生数据采集时钟信号的关系如图6所示。其中A代表理想的光栅A相脉冲信号，其每个脉冲宽度均相同，B代表理想的A相脉冲K次分频后的时钟信号CLK，分频是利用CPLD的计数器对光栅A相脉冲上升沿进行计数，理想情况下CLK信号的各个脉冲宽度均相同，C代表因光栅编码器的刻线不均匀造成的A相脉冲宽度不均匀信号，其某个脉冲的上升沿相对理想脉冲变宽了ta；由于任何信号经CPLD或FPGA变换时都将采用逻辑门电路实现，这将出现信号延迟，D代表了包含CPLD分频延迟时间td的实际CLK信号，该延迟时间取决于CPLD的型号，选用EPM7128S系列，td延迟为10 ns以内，但该延迟时间不会因输入信号的变化而变化，对测量精度影响有限。

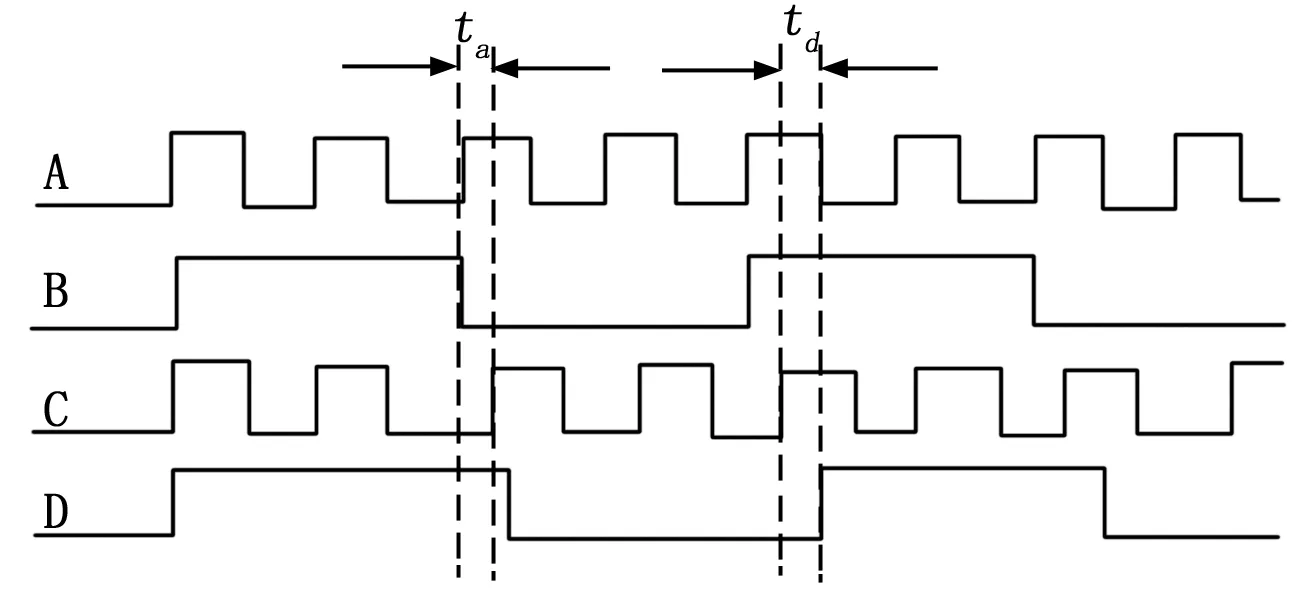
图6 光栅A脉冲分频示意图

3 数据采集软件设计

软件系统采用LABVIEW2000环境开发，动态半径测试的软件主功能模块主要包括数据采集控制、原始数据滤波、定位区域信号识别模块、动态半径计算，其功能模块如图7所示。

图7 软件功能模块图

其中，考虑到转盘形状圆度误差包含相位信息，为不丢失相位信息，采用FIR滤波器对测试信号进行低通滤波，滤波器上限选择为电容测微仪的截止频率处。对于电容测微仪上附带随机干扰，采用多圈集合平均的方法将其消除[9]，其计算方法由式(1)表示，其中N为每圈采样点数，对4圈的采样数据作集合平均。

(1)

4 实验结果与测量不确定度评定

4.1 实验结果

基于提出的动态半径测量方法，对我所研制的10-6级高精度精密离心机开展动态半径测量工作。该离心机转盘标称半径为1 m，最大输出加速度100 g，在转盘的四周垂直安装4个定位平台，可同时对4只加速度计进行标定。在测量过程中，以离心机输出加速度为0.1 g时为基准距离，分别测量离心机输出加速度在1 g、5 g、10 g、20 g、30 g、40 g、50 g、60 g、70 g、80 g、90 g、100 g的动态半径。动态半径测量电容测微仪和定位用电容测微仪所测得的原始数据分别如图8(a)、图8(b)所示。

从图8可以看出，在离心机旋转一周的过程中，两只电容测微仪同步采样1 600个点，在定位平台经过定位用电容测微仪时，该电容测微仪输出有效。图8(a)中的凸出尖峰为离心机转盘边缘上的一个凹坑，是加工时产生的。对比图8(a)与图8(b)，可以看出，定位平台避开了转盘加工精度最差的地方安装，不包含在动态半径计算的有效数据段内。经过比对判读，4个定位平台的有效数据点分别为106～121点、506～521点、906～921点、1 309～1 324点，每个有效数据段为15个点。将不同转速下离心机的有效数据段与0.1 g转速下的有

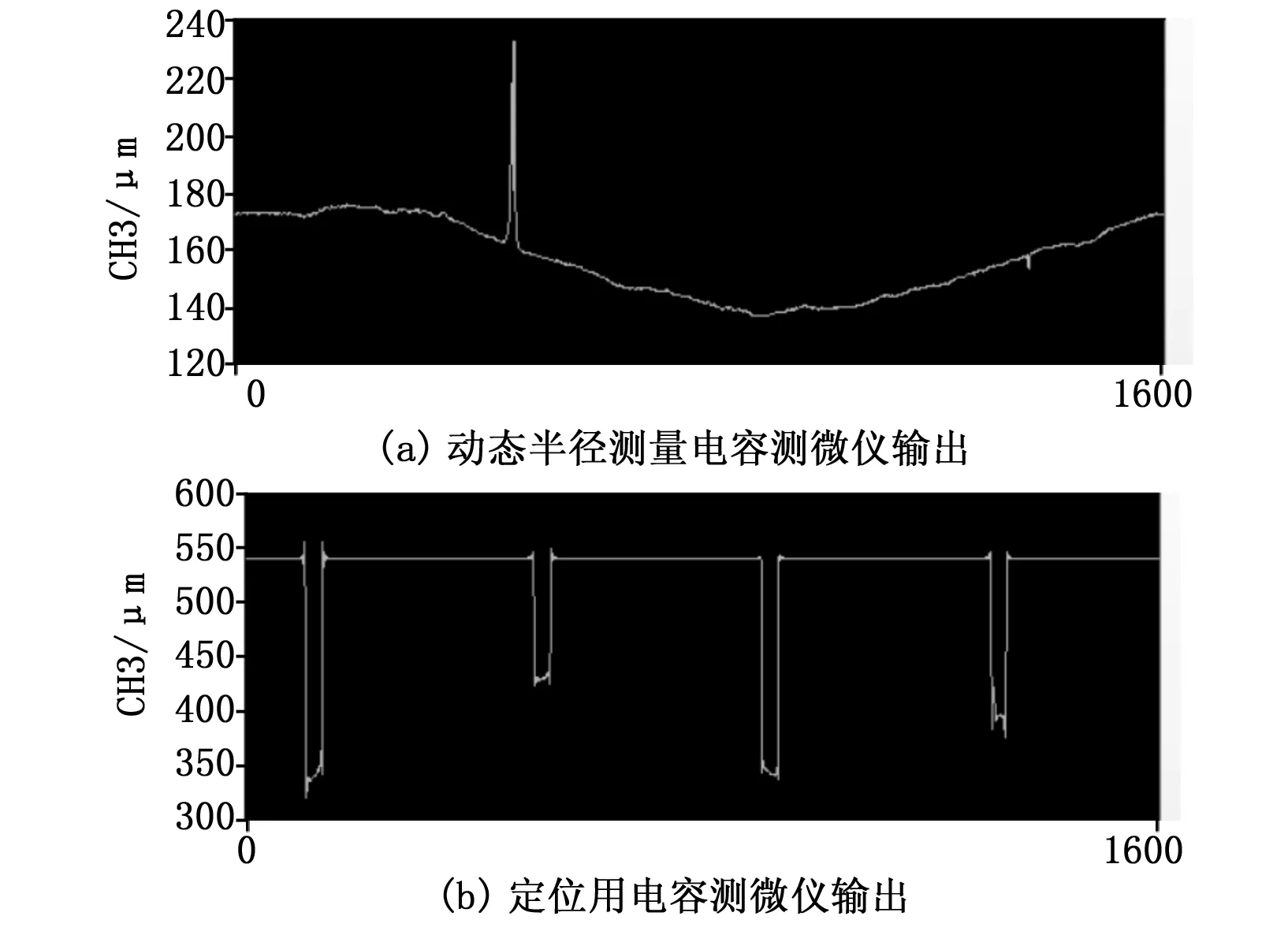
图8 电容测微仪输出数据(X轴-采样点数，Y轴—电容测微仪测头到离心机边沿距离μm)

效数据段直接比较，即可计算出每个转速下的动态半径。离心机的动态半径与其加速度输出值的关系曲线如图9所示。可以看出，离心机的动态半径随着其输出加速度的增大线性增大，4个定位区域的动态半径变化规律一致，动态半径变化与预期动力学仿真一致；还可以看出，4个定位平台所在位置的动态半径值并不完全一致，说明又不要对动态半径进行定位测量。

图9 离心机动态半径与其加速度输出值的关系曲线

4.2 测量不确定度评定

不确定度包括A类不确定和B类不确定度，其中A类不确定度为测量读数产生的不确定度，B类不确定度为测量仪器本身不确定度。A类不确定度的计算方法如下:

(2)

其中:n为重复测量次数，以1号定位平台为例，取n=10，计算测量不确定度，离心机输出加速度对于A类不确定度如表1所示。当离心机在满量程输出时，A类不确定度最大，为0.078 μm。

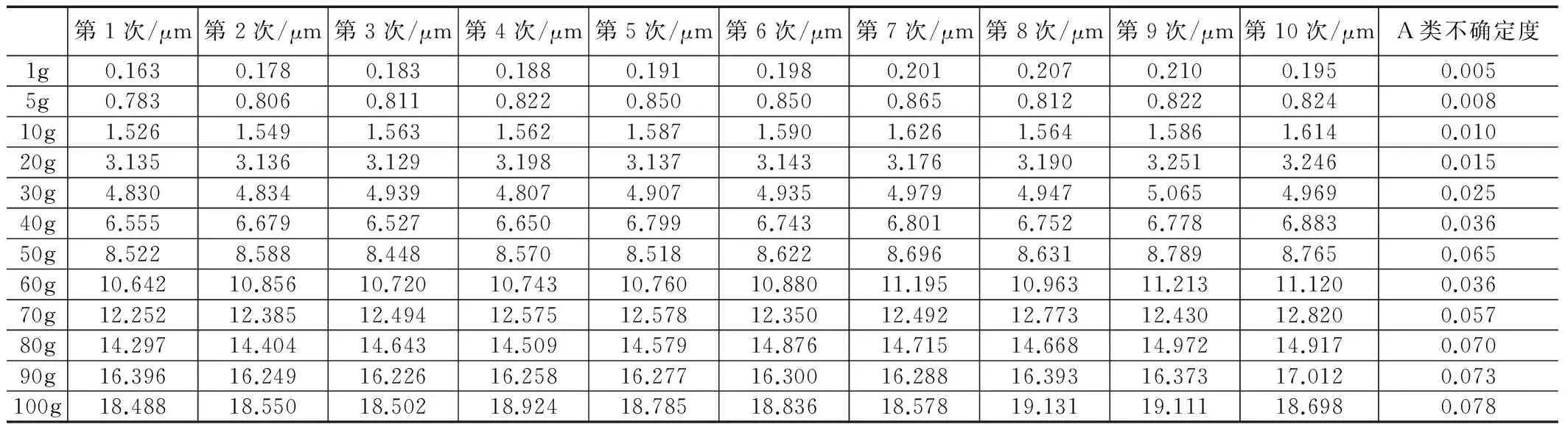
表1 测量A类不确定度统计表

测试系统B类不确定度主要来源于电容测微仪和PXI数据采集长，通过查阅相关数据手册，电容测微以B类不确定度为urs=0.042%,PXI数据采集卡的B类不确定度为urs=0.02%。

则由电容测微仪和数据采集卡系统组合的测量不确定度计算为:

(3)

设x表示动态半径测试系统的一个测量值，则其B类测量不确定度uR(x)可表示为:

(4)

由于采用外基准方式安装电容测微仪，因此，在0.1g转速下，距离最大，经测试为180.969μm。则最大B类不确定度为：

uRmax=0.047%×180.969=0.085 μm

(5)

5 结论

为了进一步提高动态半径的测量精度，提出一种基于外基准的定点定位测量方法，该方法首先对离心机动态半径数据进行等角度采用，然后精确提取精密离心机定位平台所在的转盘外边缘的局部数据，再将局部数据进行点对点的比较，计算出动态半径，消除了转盘外沿形状误差对测量精度的影响，且能够更为真实的反应加速度及安装处动态半径的变化。在我所研制的10-6级高精度精密离心机开展动态半径测量工作，对测量结果的不确定度评定表明，测量方法测量精度达到了0.085μm。

[1] 张春京.IEEE推荐的线加速度计精密离心机测试规范[J].惯导与仪表, 2001(3): 1-60.

[2] 尹小恰. 精密离心机工作半径的测试方法与误差分析[D].哈尔滨：哈尔滨工业大学, 2013.

[3]TangSZ,WangZ,JiangZX,etal.ANewMeasuringMethodforCircularMotionAccuracyofNCMachineToolsBasedonDual-frequencyLaserInterferometer[J].AssemblyandManufacturing, 2011:1-6.

[4]YamazakiK,SeinleeK.Noncontactprobeforcontinuousmeasurementofsurfaceinclinationandpositionusingdynamicirradiationoflightbeam[J].CIRP, 1993(1).

[5] 杨巨宝. 精密离心机半径值动态测试系统[J]. 宇航计测技术, 1994, 13(2): 5-10.

[6] 刘 健, 王宝光, 刘宇刘,等. 转台离心机动态半径测试方法的研究[J]. 宇航计测技术, 2006, 26(6): 1-4.

[7] 杨守琦. 大半径精密离心机可行性研究[D]. 哈尔滨：哈尔滨工业大学, 2011.

[8] 陈希军, 孙群学, 任顺清. 离心机大臂动态半径长度的测量[J]. 宇航计测技术, 2002, 22(2): 10-13.

[9] 李济顺, 洪迈生. 提高圆度误差分离精度的措施[J]. 计量学报, 1999, 20(2): 92-95.

Research and Implement on Precision Centrifuge Dynamic Radius Test

Zhou Jikun, Zhang Rong, Zhang Yi, Wang Jue, Ling Mingxiang

(Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999，China)

In order to measure the dynamic radius of precision centrifuge effectively, this paper proposes a fixed point and position measurement method based on the benchmark, and use the capacitance micrometer, 24 bits high-precision PXI data collection card set up a dynamic radius test system; In the process of test, uniform angular sampling the dynamic radius data of the centrifuge first, and accreting extraction the local date of precision centrifuge platform edge, then the dynamic radius can be calculated by comparing the local date between different speed point to point. The uncertainty evaluation of the measurement results show that the proposed test method can achieve high accuracy of precision centrifuge dynamic radius measurement, and the accuracy of precision can reach to 0.085 μm.

precision centrifuge; dynamic radius; PXI data collection

2016-01-05；

2016-01-19。

国家重大科学仪器专项(2011YQ13004702)。

周继昆(1987-)，男，重庆人，硕士，主要从事仪器仪表与测控技术方向的研究。

1671-4598(2016)06-0027-03

10.16526/j.cnki.11-4762/tp.2016.06.008

TP216

A