练习巧分层，提升练习实效

江苏省如皋市九华初级中学 王小静

练习巧分层，提升练习实效

江苏省如皋市九华初级中学 王小静

开展数学学习，必然离不开练习。练习对于数学教学的促进意义主要表现在两个方面：第一，以练习作为检验知识学习效果的工具，让学生们在解答具体问题时应用所学知识，看看大家能否独立将问题予以解决；第二，以练习作为知识学习二次深入的契机，在问题所营造的氛围中启发学生，于实际应用的过程当中深化对理论知识的理解，并继续拓展，强化学习效果。由此可见，有效的数学教学离不开练习的巧妙配合。如何将数学练习用好、用巧，也就成为了数学教师们所要思考的重点问题。

一、练习设置巧分层，展现数学问题梯度

既然学生在数学知识的学习过程当中存在着能力差异，那么，练习作为学生学习活动的延续与深化，自然也应当顺应这种能力差异而存在，让不同知识掌握情况的学生都能找到适合自己的“着陆点”。这就需要数学练习从一出现便展现出阶梯化的形态，也就是我们在这里所强调的在练习设置阶段进行分层。

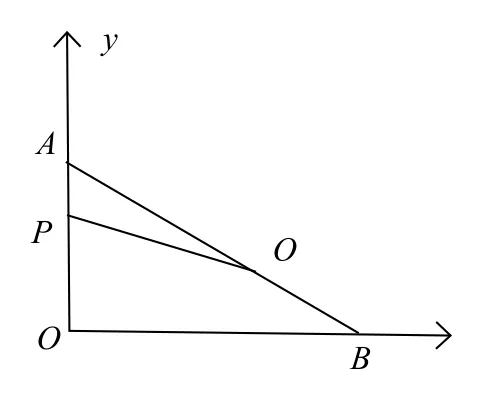
例如，在对相似三角形的练习进行设计时，我对同一个数学背景提出了三个问题，并按照由易至难的顺序进行了排列。如图，在平面直角坐标系中有点A（0，6）和点B（8，0），动点P从点A出发，在线段AO上以1单位长度/秒的速度向O运动，同时，动点Q从点B出发，在线段BA上以2单位长度/秒的速度向A运动，运动时间均为t秒。（1）直线AB解析式是什么？（2）t为何值时，以A、Q、P为顶点的三角形与△AOB相似？（3）当t为2秒时，四边形BOPQ的面积是多少？如此的梯度设置，让学生们逐个接受起来轻松了不少。

在练习设置环节进行巧妙分层，让学生们从一开始便找到了适合自己开展知识训练的位置。在初中数学当中，知识内容虽然是相同的，但对其进行练习与提问的角度却是很多的。教师们可以由此入手，尽可能多地找出对同一个知识内容进行考查的各种途径，将之按照难易程度或是呈现形式进行排序，由浅入深地展现在学生面前，让大家在练习开展之初便对数学问题的梯度有所认知。

二、题目解答巧分层，充分体现个体能力

设置练习就是为了让学生们解答这些问题，通过解答来发现数学学习的薄弱之处，有针对性地弥补和强化。因此，在分层设置的数学练习当中，解答起来必然也要随之划分出层次。教师们在设置问题时就已经初步明确了不同问题所面向的学生群体，在问题解答环节中自然也应当将这个意识贯彻下来，让学生们尽己所能、体现能力。

例如，在学习过抛物线的内容后，我请学生们阅读如下习题：抛物线y=-x2+（m-4）x+2m+4与x轴交于A（x1，0）、B（x2，0）两点，与y轴交于点C，且x1＜x2，x1+2x2=0，点D是点A关于y轴的对称点。然后，将学生们按照知识能力分为“基础组”和“拔高组”，请前者求出过点B、C、D的抛物线解析式，并请后者继续解答问题：若P是上述抛物线顶点，H是抛物线上异于C的另一点，且△BCD与△BDH的面积相等，求直线HP的解析式。在题目的分层解答过程中，学生的不同能力均得到了体现。

在初中数学的学习过程中，学生之间的知识能力已经产生出了较为明显的差异。这时，分层对其提出题目解答的要求并加以落实，便成为了高效教学的一个关键。强求能力较弱的学生解答难题，难免会打击学生自信心，而盲目要求能力较强的学生解答基础问题，显然是对学生精力的浪费。因此，在问题解答环节分层对待，是对学生个体能力的尊重，更能充分调动起每个学生的思考积极性。

三、效果评价巧分层，因生制宜适应学习

每一次练习结束后，笔者都会针对学生们在练习当中的表现进行总结评价，帮助大家找到不足，及时修正。在分层练习的背景之下，笔者也将这一指导思想落实到了课后评价当中，同样收获了十分理想的实效提升效果。

例如，在对一元二次方程的内容进行练习时，我请学生们试着解答如下问题：已知，两个连续奇数的乘积是323，求这两个奇数分别是什么。在这个问题的解答过程中，学生之中出现了不同的解题方法。对此进行总结评价时，我先肯定了大家的灵活思维，然后指出，将较小奇数设为x，另一个为（x+2）列出方程，是一个基本思路，每个学生都要掌握。接下来，将已知条件加以运用，较大奇数为x，另一奇数为323与x之商，二者相减列出方程，这也是有余力的学生应当掌握的。最后，能力最强的学生还应当能设x为任意整数，将两奇数表示为（2x-1）和（2x+1）。分层评价也表明了对学生们的差异化要求。

在以往的评价机制当中，教师们总是运用同一种评价方式来面对所有学生。有时候，教师所指出的问题并不是一些学生身上存在的，而教师所提出的学习要求，也不能被一些学生所达到。因此，对于数学练习的评价也应当进行适当分层，对不同情况的学生采取不同的评价标准，方能因生制宜，让每个学生都能够找到适合自己的练习标准，在个人能力的基础上提升练习实效。

练习是数学知识由理论向实践转化的必需环节。特别是在初中阶段的数学教学当中，从学生的心理特征来讲，具体、灵动的内容更容易将他们的关注热情调动起来。在学生的积极参与之下，教学活动的效率也能够得到显著提升。然而，每个学生的知识基础与接受能力各不相同，面对同一个数学问题的感受和思路也不一样。这时，就需要分层处理、区别对待。通过前文所述的方式，数学练习的每一个阶段都实现了因材施教，每个学生都能找到适合自己的练习内容与模式，教学效果得到了明显改善。