对初中数学教学设计的几点思考

江苏省宝应县黄塍镇中心初级中学 古建顺

对初中数学教学设计的几点思考

江苏省宝应县黄塍镇中心初级中学 古建顺

传统教学中存在着重教师作用轻学生能力培养、重预设轻生成、重知识传授轻情感激发的现象。从教学有效性的角度出发，笔者认为在数学教学中应重视对学生原有经验的设计、重视对数学问题、数学活动的设计，只有这样才能实现课堂教学由学科能力向综合能力的转化，为学生的学习设一个崭新的舞台，使学生的素质得到全面的发展。

教学设计；经验；问题；活动

教学设计的好坏直接影响着教学质量，教学设计的水平反映了教师专业水平。我们看到教学中的许多问题都是源于教学设计，要想搞好教学设计我们首先要掌握一定的教学理论，站在思想观念的高度，结合我们的教学经验，科学地进行教学设计。只有这样的教学设计才会产生有效的教学效果。

当前课程改革的根本目标是，培养学生的创新精神和创新能力，以学生的发展为本，注重全面素质的提高。在新的课程理念下，教学过程可以说是一种“沟通、理解和创新”的过程，学习不是仅仅把知识装进学生的头脑中，更重要的是要对问题进行分析和思考，从而把知识变成自己的“学识”、自己的“主见”、自己的“思想”。下面谈一谈对在数学教学设计有效性的的几点认识：

一、有效的教学设计应重视对学生原有的经验的设计

《数学课程标准》指出：数学课程“不仅要考虑数学自身的特点，更应遵循学生学习数学的心理规律，强调从学生已有的生活经验出发……数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上”。这就是说，数学教学活动要以学生发展为本。

如在讲“有理数的乘方”时，我从“折纸问题”开展教学，提出问题：“有一张厚度为0.1mm的纸，将它们对折一次，厚度为0.1×2mm，对折10次，厚度是多少毫米？对折20次厚度是多少？”在学生动手折叠纸张进行计算厚度的过程中，大部分学生计算对折10次时的厚度就显得很为难，他们表现出渴求寻找一种简便的或新的运算途径的欲望，此时，教师适时引出“乘方”的概念，用乘方表示算式0.1×220比用20个连乘简洁明了得多，其值为104.8576米，比30层楼（每层3米）还要高。

建构主义认为，学习不是简单地知识由外到内的转移和传递，而是学习者主动地建构自己的知识经验的过程，即通过新经验与原有知识经验的反复的、双向的相互作用，来充实、丰富和改造自己的知识经验。每一个学生都有自己丰富的心理世界，都有一个七彩的经验世界，对他们来说，其经验世界都是独特的。对同一个问题带着自己的经验背景，渗透着自己的个性与风格，常常表现出不同的理解，不同的问题解决策略。因此，教师不能简单地按照自己或课本中的逻辑来对学生进行理解，做出非对即错的评价，而应透视学生的理解，洞察他们的思考方式和经验背景，做出相应的教学引导，引发学生对问题的进一步思考。

二、有效的教学设计应重视对数学问题的设计

新课程重视确立学生的主体地位，提倡让学生自己去观察、自己去发问去思考、去集体讨论，从而解决问题。

传统的数学教学，总是以传播确切的和无可质疑的数学知识为己任，从教材的编写到老师讲课，呈现在学生面前的都是一个完美严谨的、系统的体系；学生平时接受的也往往是跟随型、模仿型的思维训练。这种封闭式的教学，只会使学生在前人已做定论的知识中徘徊，思维僵化，问题意识丧失，还谈什么创新与发展呢？例如，在学习“合并同类项”的内容时，我给学生出示了这么一个问题：

如图：图（1）和图（2）的“桥”都是用边长为a的正方体和长为b、宽和高都为a的长方体组成的。1）表示图（1）中“桥”的体积的代数式是什么？表示图（2）中“桥”的体积的代数式是什么？

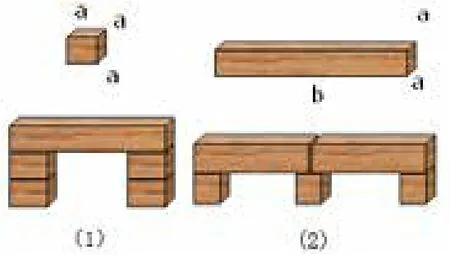
2）你能用几种方法表示两个“桥”的体积之和？与同学交流，并说说各自的理由。

当鼓励学生采用探索的方法，经历由已知出发、经过自己的努力或与同伴合作获得对新知识的理解，而不是采用“告诉”的方式；当学生面临困难时，引导他们寻找解决问题的思路，并在解决问题的过程中总结所获得的经验，而不是直接给出解决问题的方案；当学生对自己或同伴所得到的“数学猜想”没有把握时，要求并帮助他们为“猜想”寻找证据，根据实际情况修正猜想，而不是直接肯定或否定他们的猜想；当学生对他人（包括教科书、教师）的思路、方法有疑问时，鼓励他们为自己的怀疑寻求证据，以否定或修正他人的结论作为思维的目标从事研究性活动，即使学生的怀疑被否定，也应当首先对其尊重事实、敢于挑战“权威”的意识给予充分的肯定。

三、有效的教学设计应重视对数学活动的设计

《数学课程标准》指出：“数学教学是数学活动的教学，是师生之间、学生之交往互动与共同发展的过程。”这里，强调了数学教学是一种活动，是教师和学生共同的活动，这对我们树立正确的数学教学观具有重要意义。

这就要求教师在教学设计中应将重点放在揭示知识的发生过程，暴露知识的思维过程，将重结果教学向重过程的教学转变，从而使学生在教学过程中思维得到充分的训练，既长知识，又增才干，为学生的思维发展提供一个良好的训练空间。例如：在讲授判定三角形全等的边角边公理时，我先让每个学生利用直尺和量角器在白纸上作一个△ABC，使∠A=20°，∠B=60°，AB=3cm，并用剪刀剪下此三角形，然后与其他同学所作三角形进行对照，看看能否重合，这时学生们会发现是能够重合的。接下来让学生改变角度和长度大小再作三角形，剪下三角形并对照，这样学生自然会发现每次所作三角形都能够完全重合，此时教师启发学生总结出：如果两个三角形有两个角和夹边对应相等，那么这两个三角形全等，即“角边角”公理。

教学并不是一项普通的工作，而是一门艺术，创造性地使用新教材和有效地教学设计，才能真正达到育人宗旨，才能创造出教学之美，体会到教学之乐。总之，只有以新的理念为指导，从学生已有的知识经验出发，提倡问题式、活动式的教学设计，这样才能实现课堂教学由学科能力向综合能力的转化，为学生的学习设一个崭新的舞台，使学生的素质得到全面的发展。

［1］数学课程标准（实验稿）北京：北京师范大学出版社，2001.

［2］关文信新课程理念与课堂教学行动策略丛书【M】.北京：首都师范大学出版社，2003.