一种基于约束最小二乘估计的被动目标定位算法

赵锦园王磊

（1.海军驻杭州地区军事代表室，杭州，310023；2.第七一五研究所，杭州，310023）

一种基于约束最小二乘估计的被动目标定位算法

赵锦园1王磊2

（1.海军驻杭州地区军事代表室，杭州，310023；2.第七一五研究所，杭州，310023）

提出一种基于约束最小二乘法的被动跟踪定位算法，同时为降低算法复杂度，快速有效地得到实时估计的结果，引入序贯估计方法。仿真结果表明，该方法保留了最小二乘法易于工程实现的优点，又有效解决了估计偏置的问题，同时不需要进行初始值的估计，也避免了滤波发散的问题。

被动定位；纯方位目标运动分析；约束最小二乘法；序贯估计

纯方位目标运动分析（BOTMA）方法长期以来一直受到研究人员的关注，但在被动观测下，目标量测方程存在非线性。Aidata和Nardone［1］提出的伪线性最小二乘法（PLE）将量测方程进行伪线性化处理，再利用最小二乘法进行估计。该方法将非线性转换到了噪声项中，使得量测噪声存在相关性，其估计结果是有偏的［2］。为消除这种估计偏置，Holtsberg［3］给出了一个近似无偏的结果，但其更适合于批处理而非实时估计；Passeriewx等［4］和Chen［5］利用辅助变量（IV）去除估计偏置；Lindgren、Gong［6］和Aidata［7］提出了利用扩展卡尔曼滤波（EKF）的方法；Chernoguz［8］和Kirubraja［9］等提出了最大似然估计方法（MLE）。以上方法均存在算法本身对初始选择比较敏感问题。

实际工程应用中，一般利用PLE方法估计初始值，再代入到EKFMLEIV等方法中进行后续处理。然而，水声环境复杂，PLE估计的初值存在较高的偏差，难以满足实际需要。同时后续算法本身含有迭代过程或者递归过程，比较复杂，收敛速度较慢，而且需要已知误差的统计特性，宽容性也比较差。

本文在将目标量测方程进行伪线性化后，采用一种基于约束最小二乘的方法对目标运动参数进行估计，引入序贯估计方法，降低了算法复杂度，能快速有效地得到实时估计的结果。

1 问题描述

不失一般性，我们假设采样的时间间隔为1 s，对于匀速直线运动的目标，速度向量为常向量，与时间无关，于是有：

如图1所示，将本舰到目标的向量与正北方向的夹角定义为目标的真实方位，并且记i时刻目标的真实方位为。

图1 本舰和目标位置及目标方位

根据几何关系，不难得到：

由于量测误差的存在，通过本舰实际量测的目标方位与真实方位存在一定的误差，假设该误差为，并且该误差方差为。目标的量测方位可以表示为：

由式（1）可以看到目标的运动状态实际上可以由一个四维向量确定，将目标的跟踪定位问题归结为了通过带有误差的方位量测对上述四维向量的估计问题。

2 约束最小二乘估计

在式（2）中进行交叉相乘，可以得到：

在过去所应用的伪线性最小二乘法中，所采用的方法是直接通过计算一段时间的，通过选取该误差的平方和来估计目标的运动状态，该方法简单并且容易工程实现，但结果是有偏的。

进一步分析式（5）可以得到：

在最后一步中，由于误差ei取值非常小，可以近似认为。

选取时刻k0，对运动目标进行被动定位必须保证本舰在0～k0的时间段内至少完成一次有效的机动［10］，记：

表示待估计的向量。

表示误差向量，同时，令：

可以得如下关系：

对A和u进行扩维处理，令：

其中，h为某个确定常数。则有：

令

利用式（16）计算得到：

其中，

在该式中，J为常量，可以通过调整h使得

同时，还需要考虑式（14），目的是使左侧得到的误差平方和最小，令

该问题可以利用拉格朗日乘子法进行求解，构造代价函数：

对θ求偏导并令其为0，可以得到：

那么θ是矩阵对（R，W）的最小广义特征根所对应的广义特征向量。最后再利用式（13），可以得到u值，从而估计目标当前的位置。

3 序贯估计方法

在实际目标跟踪定位过程中，对于目标方位的量测值是陆续到达的，上面所提出的最小二乘估计方法都是基于批处理的，即为获得k0时刻的估计值，需要利用从0～k0时刻的方位测量，然后通过计算代入式（21）进行求解，得到估计。

当本舰接收到k0+1时刻的目标方位测量值时候，需要从头开始，通过0～k0+1时刻的方位测量值，计算代入式（21）进行求解，得到估计θk0+1。这样在每个时刻进行估计更新都必须从头算起，所需要的时间复杂度是（L为时间长度），这样难以满足快速有效的实时探测要求。

希望通过在k0时刻已经获得的某些结果的基础上，通过增量信息βk0+1直接估计θk0+1。为叙述方便，重新规定有关符号。可以获得的数据为：，表示本舰在i时刻的位置；，表示获得的i时刻的目标量测方位。

假设已经估计出0～k0时刻的目标运动状态，现在对k0+1时刻目标运动状态进行估计：

对于k0+1时刻进行估计：

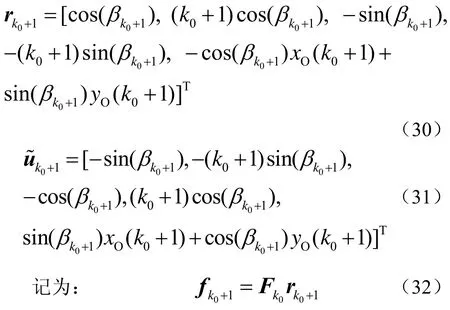
可以计算得到［11］：

并且由式（30）可以得到：

记正规化因子（Normal Factor）为：

4 仿真实验分析

为验证该算法的处理效果，进行仿真数据分析。在图2中，以本舰起始点为坐标原点（0，0），本舰的航行速度为10 m/s，在0～100 s之间沿着x坐标方向移动，100 s时刻进行90°机动，再沿着y坐标方向移动，200 s时刻进行机动，沿着x坐标方向移动，300 s时刻进行机动，再沿着y坐标方向移动。同时，目标的起始位置为（3 000 m，4 000 m），速度为（7 m/s，-6 m/s）。在被动探测条件下，本舰只能获得目标的方位，并且测量方位值存在方差为1°的误差。

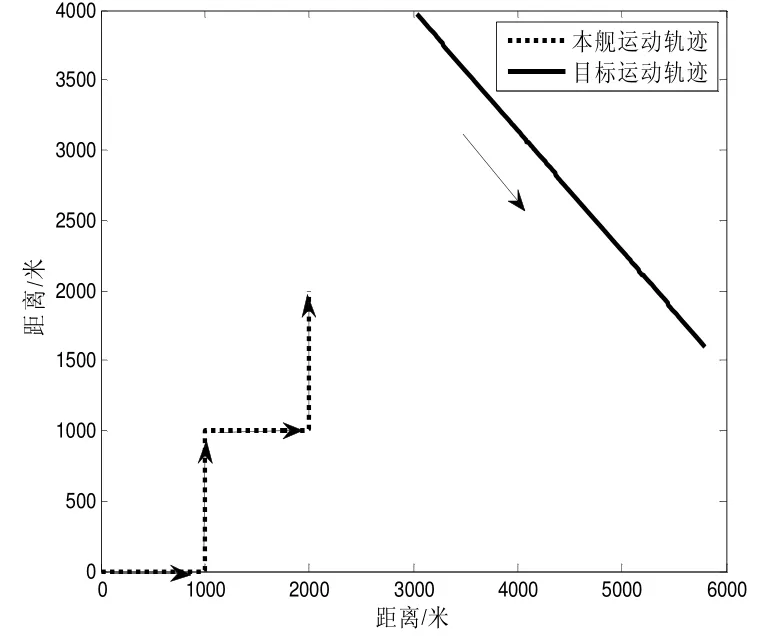
图2 本舰运动轨迹和目标态势

图3给出的是批处理情况下，约束最小二乘法与伪线性最小二乘法对目标进行跟踪定位效果的对比。可以看出，伪线性最小二乘法有较大的偏差，而本文所采用约束最小二乘法估计的轨迹精度获得了大幅度的提高。

图3 约束最小二乘法与伪线性最小二乘法对比（批处理）

图4中，为进行快速有效地实时估计，采用了序贯估计方法，同样获得了实时条件下约束最小二乘法与伪线性最小二乘法对目标进行跟踪定位的对比效果。从图中可以看出，伪线性最小二乘法估计的目标位置有明显的偏置，而且随着时间的积累，该偏置并不能逐步消除，而本文所采用约束最小二乘法估计极大地改善了这种偏置，获得了更准确的定位效果。

图4 约束最小二乘法与伪线性最小二乘法对比（实时估计）

为分析跟踪定位的误差，引入相对误差作为衡量定位效果的精度，对于x轴方向，我们定义x轴向精度为（目标x坐标估计值-本舰x坐标）/（目标x坐标实际值-本舰x坐标）；同理，对于y轴方向，我们定义y轴向精度为（目标y坐标估计值-本舰y坐标）/（目标y坐标实际值-本舰y坐标）。

图5和图6为算法经过100次蒙特卡洛仿真的结果。从图中可以看出，在经历一段时间（150 s）以后，本文所用约束最小二乘估计方法在两个方向上的精度都有了大幅提高，有效地抑制了传统伪线性最小二乘估计存在偏置的问题，获得了较好的跟踪定位效果。

图5 约束最小二乘法算法的x轴方向定位精度

图6 约束最小二乘法算法的x轴方向定位精度

5 结论

本文提出了一种基于约束最小二乘估计的被动目标跟踪定位方法，该算法较好的解决了被动观测下量测模型和目标运动模型的非线性问题。

该方法不需要进行初始值的估计，避免了卡尔曼滤波中可能出现的滤波发散的问题。同时，保留了最小二乘法易于工程实现的优点，又可以改善伪线性最小二乘法的偏置问题，提高跟踪定位的精度。序贯估计方法的引入，进一步降低了算法复杂度，能快速有效地得到实时估计的结果。进行了仿真实验，结果表明该方法相对于伪线性最小二乘估计，获得了更加有效的跟踪定位精度。对于单舰的被动跟踪定位应用，有一定的工程参考价值。

［1］AIDATA V J，NARDONE S C.Biased estimation properties of the pseudolinear tracking filter［J］.IEEE Trans.Aerosp.Elecron.Syst.，1982，AES-18:432-441.

［2］GAVISH M，WEISS A J.Performance analysis of bearings-only target location algorithms［J］.IEEE Trans.Aerosp.Electron.Syst.，1992，23:817-828.

［3］HOLSBERG A，HOLST J H.A nearly unbiased inherently stable bearing-only tracker［J］.IEEE.Ocean.Eng.，1993，OE-18: 138-141.

［4］PASSERIEWX J M，PILLON D，BLANC-BENON P，et al.Target motion analysis with bearings and frequencies measurements via instrumental variable estimation［C］.Proc.IEEE Int.Conf.Acoust.，Speech，Signal Process，1989: 2645-2648.

［5］CHAN Y T，RUDNICKI S W.Bearings-only and Doppler-bearing tracking using instrumental variables［J］.IEEE Trans.Aerosp.Electron.Syst.，1992，28（4）: 1076-1083.

［6］LINDGREN A G，GONG K F.Position and velocity estimation via bearing observations［J］.IEEE Trans.Aerosp Elecron.Syst.，1978，AES-14:564-577.

［7］AIDATA V J.Kalman filter behavior in bearings-only tracking applications［J］.IEEE Trans.Aerosp Elecron.Syst.，1979，AES-15:29-39.

［8］CHERNOGUZ N G.A smoothed Newton-Guass method with application to bearings-only position location［J］.IEEE Trans.Aerosp.Electron.Syst.，1995，43（8）:2011-2013.

［9］KIRUBRAJAN T，BAR-SHALOM Y.Low observable target motion analysis using amplitude information［J］.IEEE Trans.Aerosp.Electron.Syst.，1996，32:1367-1384.

［10］SONG T L.Observablity of target with bearings-only measurements［J］.IEEE Transaction on Aerospace and Electronic Systems，1996，32（4）:1468-1472.

［11］RAO Y N，PRINCIPE J C.An RLS type algorithm for generalized eigendecomposition［C］.Proc.IEEE Signal Processiong Workshop Neural Networks Signal Processing，2001:263-272.