考虑温度作用的顶部搭板悬臂式挡墙分析

王波，徐波

（深圳市市政设计研究院有限公司,广东 深圳 518029）

考虑温度作用的顶部搭板悬臂式挡墙分析

王波，徐波

（深圳市市政设计研究院有限公司,广东 深圳 518029）

设计仅用来支挡土压力的悬臂式挡墙在墙顶搭板后，其墙身结构受力特征会发生显著改变。现在分析悬臂式挡土墙土压力计算方法的基础上，建立了悬臂式挡土墙三维数值计算模型，研究其顶板温度作用对悬臂式挡土墙结构受力的影响。计算结果表明：在土压力和顶板升温共同作用下，挡土墙外侧中部的最大拉应力超过混凝土最大抗力，立墙外侧中部将产生裂缝；在土压力和顶板降温共同作用下，挡墙内侧底部最大拉应力超过混凝土最大抗力，立墙内侧底部将产生裂缝。有限元计算结果与实际情况基本相符，说明计算结果可信，符合实际情况。据此，对结构病害提出了加固建议。

道路工程；悬臂式挡土墙；温度变化；有限元

0　引言

悬臂式挡土墙为钢筋混凝土结构[1]，它充分利用了填料的自重提高整体稳定性，因具有结构轻，圬工省，占地少[2-4]的优点，在水利工程中应用十分广泛。随着建设发展，既有悬臂挡墙可能会与其他结构，如桥梁、道路、建筑等相互搭接，使得悬臂挡墙在已经承受土压力的同时，又受到搭接结构的作用，导致挡墙受力特征改变并产生新的问题。

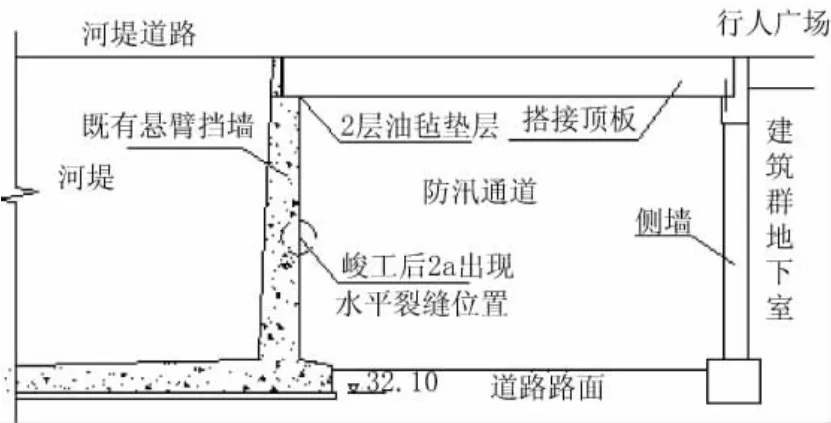
图1　顶部搭板的悬臂式挡墙结构示意图

图1所示为某长达3 km的沿河道路路肩悬臂式挡墙墙顶搭板实例的剖面示意。因开发需要，该道路挡墙在墙体已经建成、大部分墙后尚未开始填土时，距墙8 m处建筑群采用钢筋混凝土顶板跨越建筑与挡墙之间的防汛通道，将建筑一层行人广场与河堤道路连接起来。其连接方式为：将长约8.5 m的钢筋混凝土顶板一端置于建筑侧墙上（采用固支），另一端搁置在悬臂式挡墙顶部，顶板与墙顶之间垫2层油毛毡。搭板施工后，继续完成道路施工。工程完工后，行人广场直接通往河堤道路，便于人们出行。

但是这样搭接后，悬臂挡墙由原来仅承受填土土压力作用的结构，变成了还需承受搭接顶板传来的结构重量、行人荷载及温度应力的结构，完全改变了悬臂式挡土墙的受力状况。而这种情况，目前还没有文献提到过，工程人员对该种结构的受力特征也没有深刻认识，反而认为，墙顶增加了支撑，对挡墙稳定性有帮助。但是事实是，该工程的墙竣工2 a后，墙身外侧中部普遍发现如图2所示水平长直裂缝，裂缝位置如图1标注所示。

为揭示这种悬臂式挡墙墙顶搭板结构的工程特性，也为了对产生裂缝的墙体提出适当的加固建议，本文在探讨悬臂式挡墙土压力计算方法的基础上，利用有限元对其受力特征进行分析，并提出了加固建议。其成果可供同行参考。

1　悬臂挡墙的土压力计算

挡墙土压力计算一般采用朗肯理论或库仑理论计算。但是悬臂式挡墙的土压力计算有一定特殊之处[5]：因为悬臂式挡墙墙背虽然竖直，但由于底板的存在，其破坏面不是立墙背面，因此不宜直接采用上述土压力理论计算立墙所受土压力。如图3所示，悬臂式挡土墙在填土压力的作用下，墙体产生背离填土方向的位移和变形，其值达到一定值时，墙后填土即处于主动极限平衡状态，此时填土内将产生以墙脚C点为基准点的两个滑动面，即：CE面和AC面。

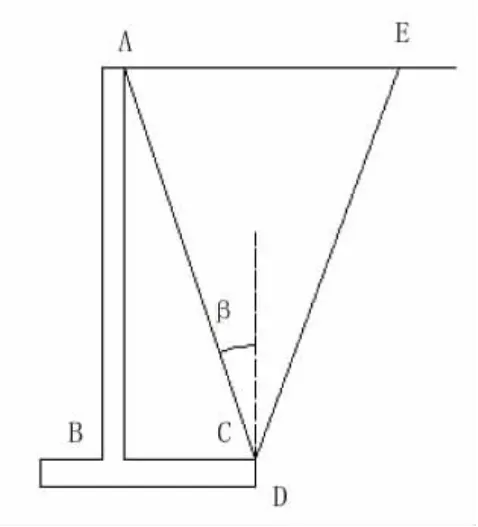
图3　悬臂式挡土墙立墙滑体示意图

这里，AC面可称为计算墙面，即设想填土所产生的主动土压力是作用在AC面上的。然后压力通过土体ABC传递到立墙AB上。作为计算墙面，AC面与竖直面之间的夹角β应满足条件：

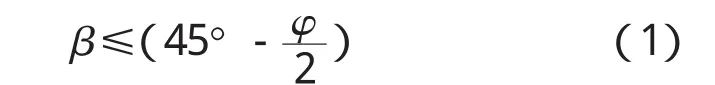
式中：φ为填土的内摩擦角。

如若：

则：应从C点作与竖直面的夹角等于45°-φ/2的平面CF作为计算墙面[6]。

假想墙背AC的土压力计算可以采用库伦土压力理论进行计算，计算方法不需赘述[7]。但立墙墙背AB的土压力值则需要在AC面计算结果的基础上进一步考虑ABC（或ABCF）土体受力后才能得到。其计算过程如下：假设从土体ABCF中取出一个厚度为dz，距填土表面的深度为z的微分土层abcd，则在该土层上的作用力如图4所示。

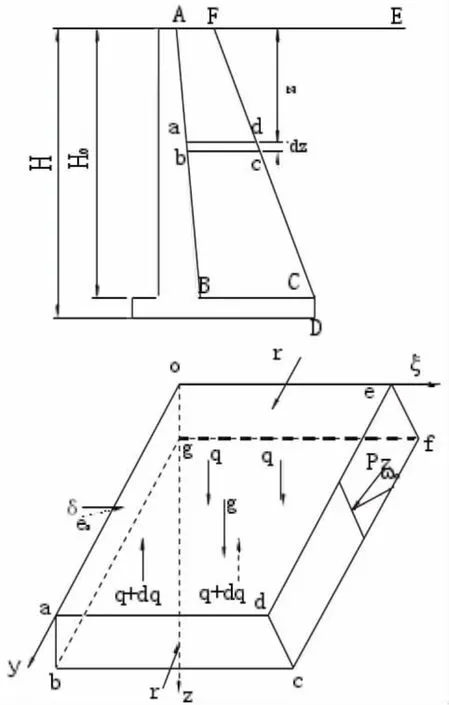
图4　悬臂式挡土墙土压力计算简图

在微分土层上作用有土层的重力g，作用方向竖直向下；土层顶面的竖直正应力q，均匀分布在土层顶面oade上，作用方向向下；土层底面的的竖直正应力(q+dq)，均匀分布在土层底面 bcfg上，作用方向向上；在计算墙面dcfe上作用有主动土压力Pz，均匀分布在面积dcfe上，作用方向指向立墙，作用线与dcfe面的法线成φ0角（φ0为填土的内摩擦角），位于法线的上方；在靠立墙的平面oabg上，作用有侧向土压力ez，均匀分布在oabg面上，作用方向指向填土，作用线与oabg平面的法线成δ角，位于法线的下方；考虑到沿挡土墙长度方向，土体之间无相对位移，故在土层两侧平面abcd和oefg上法向反力r，作用方向指向土层。根据静力平衡条件Σx=0，通过理论推导可以得出：

（1）当填土表面作用均布荷载q0时，由平衡条件Σx=0可得:

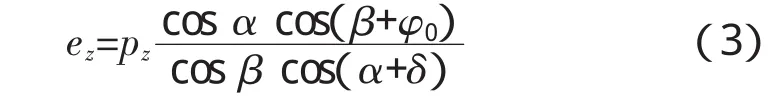
则：

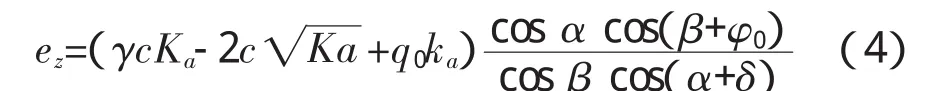
（2）当填土表面无荷载作用时：

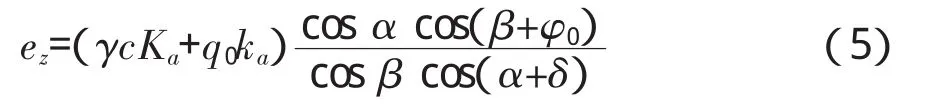
2　顶部搭板的悬臂式挡土墙有限元模型

2.1有限元模型

根据图1所示结构的实际参数，采用商业有限元软件计算。选取单位宽度挡土墙与顶板结构建立模型（见图5），其几何尺寸如下：顶板为梁板式，板厚150 mm，梁350 mm×750 mm(梁高含板厚)，梁板总长8 660 mm（净跨8 000 mm，两端支撑各330 mm）；挡墙立墙为变厚度，顶部500 mm，底部780 mm，墙高6.0 m。挡墙立墙设计墙身内侧配筋B18@150；外侧配架立筋B12@200。

图5　有限元计算模型图

挡土墙混凝土强度等级为C25，梁板结构混凝土强度等级为C30，结构钢筋为HRB335，其截面面积、长度和间距均按实际情况计入模型。混凝土采用C3D8I八节点线性六面体单元，非协调模式，共划分1 376个单元；钢筋采用T3D2两结点线性三维桁架单元，共划分8 391个单元。混凝土采用rusch简化模型，钢筋采用理想弹塑性模型，混凝土的线膨胀系数为1×10-5/℃。

2.2边界与荷载条件

模型边界条件按现场条件确定：梁板右端固定在建筑群侧墙上，视为固定支座；左端与挡土墙顶接触，中间垫2层油毛毡，取接触面切向摩擦系数取0.35；挡土墙底部固定。

结构荷载按实际情况考虑，主要为结构自重荷载、土压力和温度应力。因顶板上部不行车、只有少量行人，故荷载考虑如下：

（1）土压力根据式（4）或式（5）计算后按面荷载考虑作用在立墙上，墙背压实填土（压实度0.92以上） 取按原设计值γ=20 kN/m3，c=11.9 kPa，ψ=18°。

（2）结构自重按实际情况考虑（钢筋混凝土γ=24 kN/m3，重力加速度9.8 m/s2)。顶板行人荷载考虑4 kN/m2；当行人荷载对结构受力有利时，不考虑行人作用。

（3）结构初始温度设置为20℃，结合气候条件，为简化考虑，温度荷载按下列几种情况选取：

a.升温：板升温至40℃，挡土墙与土接触部位降温至15℃，结构剩余部分不变。

b.升温：梁板一起升温至40℃，挡土墙与土接触部位降温至15℃，结构剩余部分不变。

c.降温：板降温至0℃，结构剩余部分不变。

d.降温：板降温至0℃，挡土墙与土接触部位降温至15℃，结构剩余部分不变。

e.降温：梁板一起降温至0℃，结构剩余部分不变。

f.降温：梁板一起降温至0℃，挡土墙与土接触部位降温至15℃，结构剩余部分不变。

3　有限元分析结果

根据问题特征，选取具有三个代表性的工况进行描述。分别描述每种工况的应力场、塑性应变场[8-9]，并分析如下。

3.1不考虑温度作用

图6～图8为仅施加重力和土压力等直接荷载的悬臂式挡土墙应力云图，其中S22为竖向的应力，正值为拉应力，负值为压应力。

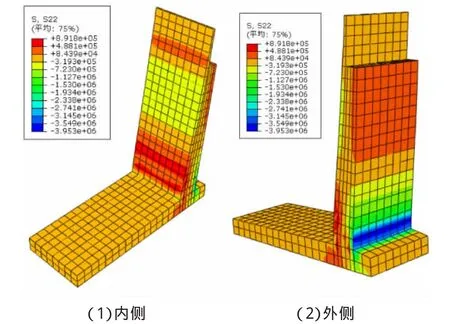
图6　挡土墙混凝土应力图（不考虑温度作用）

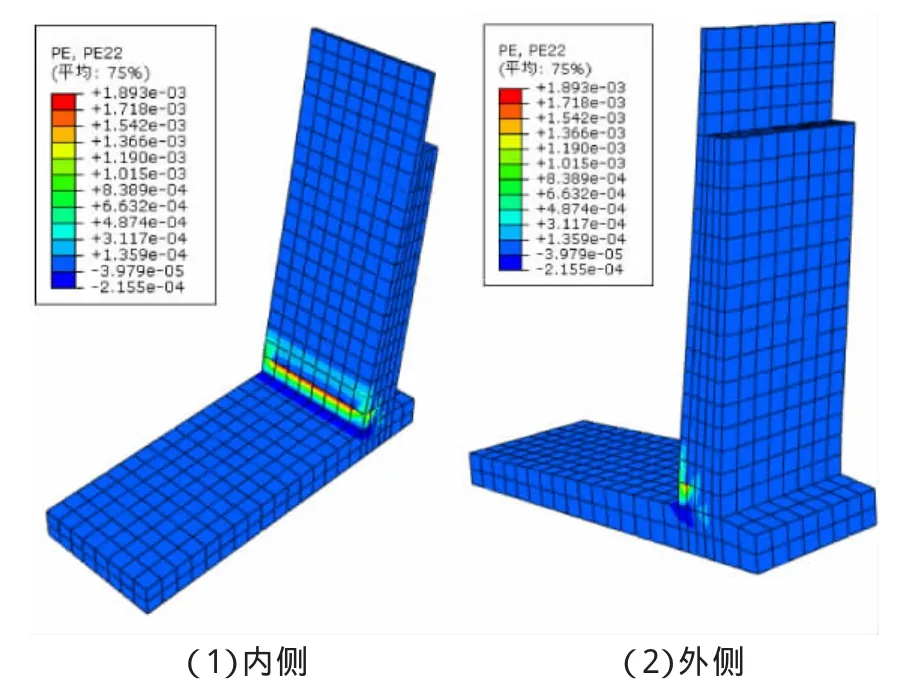
图7　挡土墙混凝土塑性应变图（不考虑温度作用）

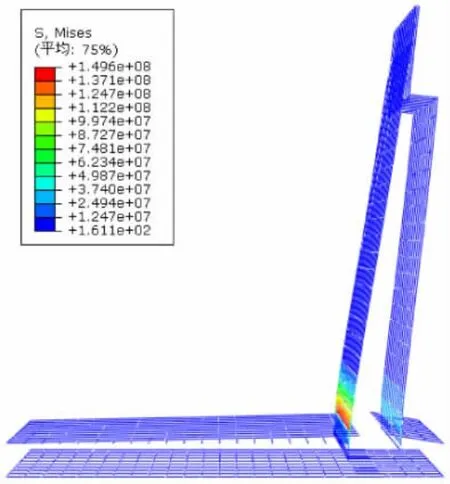
图8　挡土墙钢筋不考虑温度作用的Mises应力图

计算结果表明，在重力、土压力等直接荷载作用下，挡土墙混凝土变形较小，最大拉应力为0.82 MPa，未超过墙身混凝土抗拉强度标准值1.78 MPa[10]，拉应力值较小，立墙外侧未见塑性应变。所以，可认为挡土墙在重力、土压力荷载作用下基本处于弹性状态，挡土墙外侧无裂缝。

3.2升温作用

图9～图11为在土压力、自重等各种荷载作用基础上，对结构施加升温温度作用，得到的墙体竖向应力云图。

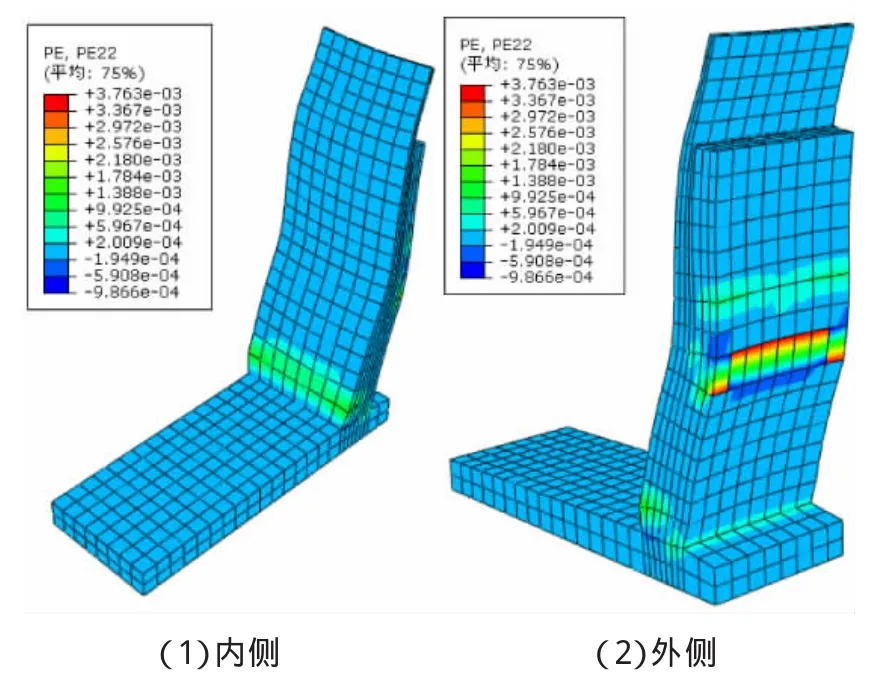
图9　挡土墙混凝土应力图（考虑升温作用）

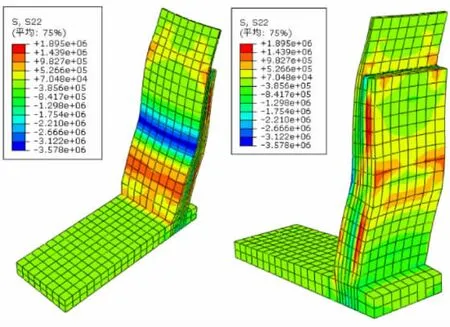
图10　挡土墙混凝土塑性应变图（考虑升温作用）

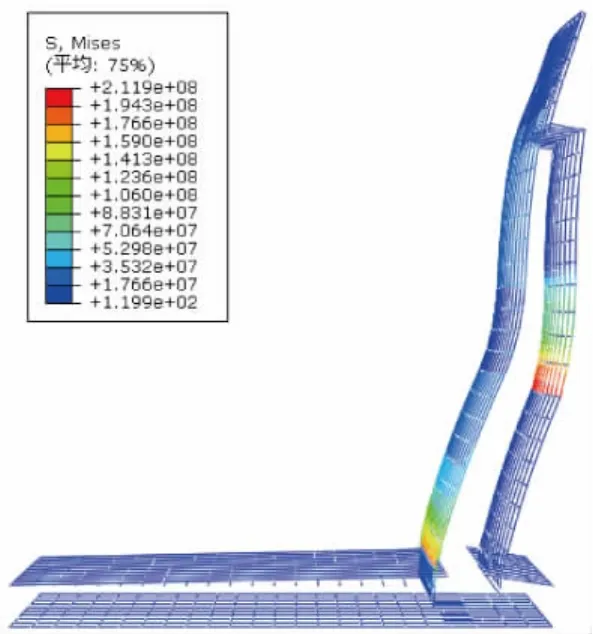
图11　挡土墙钢筋Mises应力图（考虑升温作用）

分析结果表明，在重力、土压力等荷载作用基础上，对结构施加升温作用，挡土墙混凝土变形增大，最大拉应力达到1.9 MPa，超过了其混凝土抗拉强度标准值；挡土墙墙面外侧中部处出现集中塑性变形，结合应变图可知该位置拉应力较大，接近或超过混凝土最大拉应力，同时对应位置墙体内侧也有较大的压应力。

所以，可认为在土压力与升温共同作用下，挡土墙立墙外侧中部会出现裂缝。其原因主要是梁板升温产生的推力通过顶板与墙顶0.35的摩擦系数传递，使得挡墙在切向作用与土压力共同作用下，立墙中部产生较大弯矩引起裂缝。

3.3降温作用

图12～图14为在直接荷载作用基础上，对结构施加降温温度作用，得到的墙体竖向应力云图。

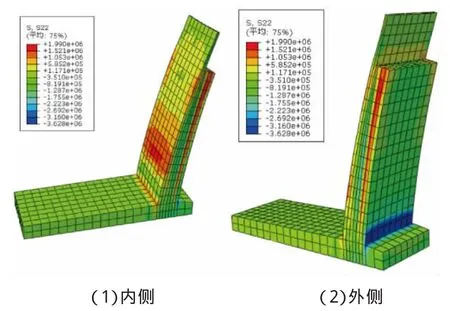
图12　挡土墙混凝土应力图（考虑降温作用）

图13　挡土墙混凝土塑性应变图（考虑降温作用）

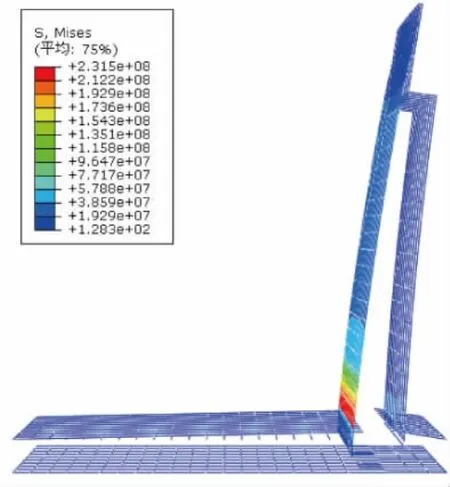
图14　挡土墙钢筋Mises应力图（考虑降温作用）

分析结果表明，在重力、土压力等荷载作用的基础上，再对结构施加降温温度作用，挡土墙立墙内侧根部会出现较大拉应力，其最大拉应力达1.99 MPa，超过了混凝土抗拉强度标准值。所以，可认为在土压力、结构自重与降温共同作用下，挡土墙立墙内侧底部可能出现裂缝。

4　处治建议

根据分析结果可知，悬臂式挡墙顶部搭板后，虽然抗滑移和抗倾覆稳定性会提高，但在温度、土压力等荷载共同作用下，挡墙墙身会产生新的结构问题：

（1）环境升温时，挡土墙混凝土变形增大，墙身最大拉应力可能会超过混凝土的抗拉强度标准值，因此，挡土墙立墙外侧中部会产生裂缝。

（2）环境降温时，挡土墙立墙底部出现较大拉应力，最大拉应力可能超过混凝土的抗拉强度，挡土墙立墙内侧底部可能会出现裂缝。

实例现场检查结果表明，该悬臂挡墙的立墙外侧中部普遍确实产生了明显裂缝，与有限元分析结果完全符合。可以推测，该挡墙立墙内侧根部也出现了裂缝。所以对挡土墙外侧中部裂缝、内侧底部裂缝都应进行适当处治以确保挡墙安全和耐久性。根据分析结果，最后提出加固建议如下：

（1）在悬臂挡墙的立墙外侧黏贴碳纤维布，提高立墙外侧抗弯能力，对中部水平裂缝进行处治。

（2）立墙内侧根部的开裂已无法直接加固。因此，提出：对建筑与挡墙之间防汛通道的道路路面予以改造，将现混凝土路面板改造成钢筋混凝土板，并且提出，在满足防汛通道净空标高的前提下，尽量提高路面的标高，这样起到减小挡墙悬臂高度、加强挡墙底部支撑，减小立墙内侧底部弯拉应力的作用。

限于篇幅本文暂不涉及具体加固措施。

5　结　论

本文在分析悬臂式挡土墙土压力计算方法的基础上，结合工程实例建立了悬臂式挡土墙三维数值计算模型，分析了考虑环境温度变化和土压力共同作用对悬臂式挡土墙受力及变形的影响，主要得出了以下的结论：

（1）设计用于抵挡土压力的悬臂式挡墙顶部搭设顶板后，顶板升温可导致中部产生裂缝；而顶板降温则可增大立墙底部弯矩，导致底部产生新的裂缝。

（2）实际工程挡墙立墙外侧裂缝与计算结果吻合，说明计算结果符合实际情况。根据分析计算结果，对该问题提出有针对性的加固建议。

[1]李海光，等.新型支挡结构设计与工程实例[M].北京：人民交通出版社，2004.

[2]陈忠达.公路挡土墙设计[M].北京：人民交通出版社，1999.

[3]Clayton,C.R.I.,Symons,I.F.and Hiedra Cobo,J.C.The pressure of clay backfill against retaining structures[J].Canadian Geotech. Journal,1991,28(April),282-297.

[4]刘晓立，严驰，吕宝拄，等.柔性挡墙在砂性填土中的土压力试验研究[J].岩土工程学报，1999，21(4):505-508

[5]Joseph G.Bentler,Joseph F.Labuz.Performance of a Cantilever Retaining Wall[J].Journal of Geotechnical and Geoenvironmental Engineering,2006.（132）:1062-1070.

[6]梁波，王家东，葛建军，曹元平.青藏铁路L型挡土墙的土压力实测与分析[J].岩土工程学报，2004，26(5)：627-631.

[7]顾慰慈.挡土墙土压力计算手册[M].北京：中国建材工业出版社，2005.

[8]陈忠达，汪东升，王志谦，高江平.悬锚式挡土墙有限元分析[J].公路交通科技，2005，22(1)：38-41.

[9]Cloug h G W,Duncan J M.Finite element analyses of retaining wall behavior[J].J.Soil Mech.Foundation,1971,97(12): 1657-1673.

[10]GB50010-2010，混凝土结构设计规范[S].

U417.1+12

A

1009-7716（2016）10-0144-05

10.16799/j.cnki.csdqyfh.2016.10.046

2016-07-01

王波（1974-），男，辽宁本溪人，高级工程师，注册规划师，交通专业总工程师，从事城市交通规划方面的研究工作。