二级悬臂式挡土墙的力学分析
2017-07-19苏利亚
苏利亚
(内蒙古科技大学建筑与土木学院,内蒙古 包头 014010)
二级悬臂式挡土墙的力学分析
苏利亚
(内蒙古科技大学建筑与土木学院,内蒙古 包头 014010)
采用ANSYS软件对二级悬臂式挡土墙进行位移和应力分析,确定一阶悬臂式挡土墙重点分析X方向的位移和Y方向的位移,二阶悬臂式挡土墙重点分析其墙背和墙踵面的受力情况;绘制出相应位置的位移和应力的分布曲线图,找到其规律,为以后的设计施工提供一定的参考。
悬臂式挡土墙;ANSYS;土压力
1 二级悬臂式挡土墙的有限元模型建立
在本模型中需要输入以下材料参数,弹性模量、重度、泊松比;内摩擦角与黏聚力是材料抗剪强度的两个力学指标,而在本例中认为挡土墙为弹性体,因此可不设内摩擦角与黏聚力。
如图1所示,第一阶悬臂式挡土墙在上部,基底放置在土体上;第二阶悬臂式挡土墙在下部,基底放置在岩体上。第一阶挡土墙墙背坡度比为1∶0.05,腋宽0.5 m,腋高0.3 m,基础埋深0.3 m,底部宽度2.5 m,顶宽0.3 m,挡土墙总高4.5 m。第二阶挡土墙墙背坡度比为1∶0.05,腋宽0.8 m,腋高1.3 m,基础埋深0.5 m,底部宽度3.1 m,顶宽0.6 m,挡土墙总高4.5 m。
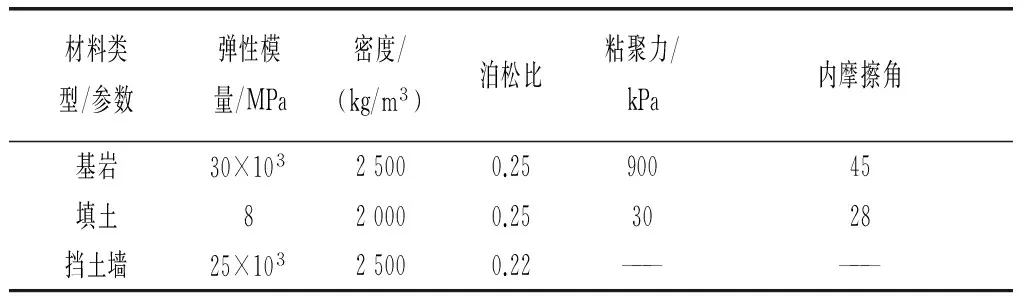
表1 计算参数
Plane82能很好的支持自动网格划分,所以本例采用自动网格划分工具,网格划分的最终结果见图2。只考虑重力场作用,不考虑其它荷载。

图1 整体模型简图
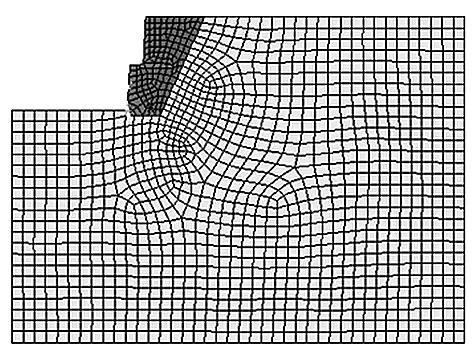
图2 模型整体网格划分
2 挡土墙位移分析
图3是分别在第一阶悬臂式挡土墙和第二阶悬臂式挡土墙墙背上取点,得到的X方向位移曲线图。
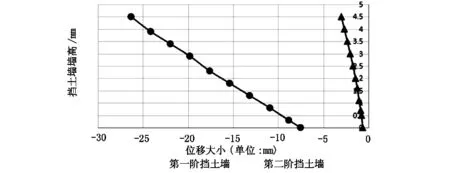
图3 挡土墙背X方向位移
由图3可以看出,挡土墙X方向最大位移发生在第一阶挡土墙距墙底4.5 m处,最大位移为26.32 mm。最小位移处发生在第二阶挡土墙距墙底处。第二阶挡土墙最大位移也仅为2.99 mm。
图4是分别在第一阶悬臂式挡土墙和第二阶悬臂式挡土墙墙底取点,得到的Y方向位移曲线图。

图4 挡土墙背Y方向位移
由图4可以看出,整体上第一阶挡土墙位移从墙趾端到墙踵端逐渐减小,大体上成线性分布,第二阶挡土墙墙底Y方向位移整体都趋近与零。墙底最大位移发生在第一阶悬臂式挡土墙距墙趾端处,最大位移为40.19 mm。
3 挡土墙应力分析
(1)由X方向应力云图可以看出挡土墙X方向拉应力最大的地方发生在第二阶悬臂式挡土墙的墙踵面上,因此这里也是挡土墙危险的地方,所以在下面具体的数据分析中着重分析第二阶悬臂式挡土墙墙踵面上X方向的应力。
通过ANSYS软件在第一阶悬臂式挡土墙墙踵面上取点,从距离墙趾端0.7 m处开始取点,一直取到第一阶悬臂式挡土墙墙踵面端部;在第二阶悬臂式挡土墙在墙踵面上取点,从墙背与墙踵面连接处开始取点,一直取到第二阶悬臂式挡土墙墙踵面端部,得到X方向拉应力曲线图5。
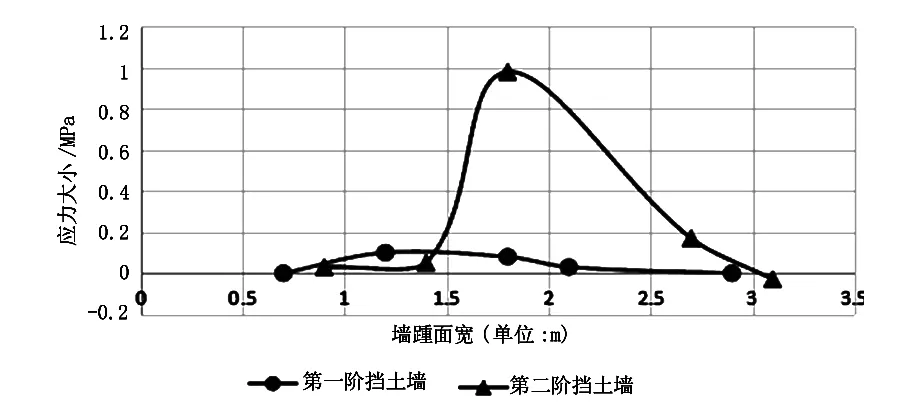
图5 挡土墙墙踵面X方向拉应力
通过图5可以看出第一阶悬臂式挡土墙和第二阶悬臂式挡土墙在墙踵面X方向均为受拉状态,其X方向应力曲线像一条开口向下的抛物线。因为第一阶悬臂式挡土墙放置在土体里,并且处于模型上部,其墙踵面拉应力较小,最大拉应力为0.1 MPa,远小于C20混凝土抗拉强度设计值。第二阶挡土墙由于岩石的限制,并处于模型下部,所以墙踵面拉引力较大,最大拉应力为0.98 MPa,接近C20混凝土抗拉强度设计值1.10 MPa,所以在第二阶挡土墙墙踵面上应该加横向抗拉钢筋。
(2)由Y方向应力云图可以看出挡土墙最大竖向拉应力发生在挡土墙墙背上,最大拉应力值发生在第二阶悬臂式挡土墙墙背与墙踵面相交的位置,这里也是挡土墙容易发生破坏的地方,在下面具体分析中也会着重分析第二阶悬臂式挡土墙墙背上Y方向的应力。
通过ANSYS软件在第一阶悬臂式挡土墙在墙面上取点,从墙背与墙踵面连接处开始取点,一直取到第一阶悬臂式挡土墙墙顶;在第二阶悬臂式挡土墙在墙背上取点,从墙背与墙踵面连接处开始取点,一直取到第二阶悬臂式挡土墙墙顶。得到Y方向拉应力曲线图6。

图6 挡土墙Y方向拉应力
由图6可以看出第一阶悬臂式挡土墙和第二阶悬臂式挡土墙在墙背均表现出拉应力,第一阶悬臂式挡土墙墙背Y方向拉应力,比第二阶悬臂式挡土墙小的多,从墙底开始在距离墙底2.9 m的位置达到最大拉应力,最大拉应力为0.21 MPa。第二阶悬臂式挡土墙墙背拉应力较大,第二阶挡土墙最大拉应力发生在墙高1.9 m处,最大拉应力为1.03 MPa,已经非常接近C20混凝土抗拉强度设计值1.10 MPa,因此第二阶悬臂式挡土墙墙背必须根据实际情况加设纵向抗拉钢筋。
4 结 论
(1)放置在土体里的第一阶悬臂式挡土墙位移较大应力较小,放置在岩体上的第二阶悬臂式挡土墙应力较大位移较小。
(2)悬臂式挡土墙墙背X方向的位移从墙底到墙顶位移逐渐增大,放置在土体上的第一阶悬臂式挡土墙比放置在岩体上的第二阶悬臂式挡土墙位移值大的多。
(3)悬臂式挡土墙墙底Y方向位移从墙趾端到墙踵端位移逐渐减小,放置在土体上的第一阶悬臂式挡土墙比放置在岩体上的第二阶悬臂式挡土墙位移值大的多。
[1] 赵明华,俞晓,王贻荪.土力学与基础工程[M],武汉:武汉理工大学出版社,2009.
[2] 王景环.新型悬臂式挡土墙有限元分析[D].环江西省水利科学研究院,2012.
[3] 傅志明.二级垛式悬臂式挡土墙动土压力分析[D].江西理工大学学报,2015.
A dissereation on two-stage mechanical analysis of cantilever retaining wall
SU Li-ya
(Architecture and Civil Engineering School, Inner Mongolia University of Science and technology, Baotou, Inner Mongolia 014010, China)
This paper used ANSYS software on two level hanging arm type block wall for by force analysis, determine a order hanging arm type block wall focus analysis x direction of displacement and y direction of displacement, second-order hanging arm type block wall focus analysis its wall back and wall heel surface of by force situation, found its law. Provide a reference for the design and construction for the future.
cantilever retaining walls;ANSYS;earth pressure
2016-09-02
苏利亚(1973-),女,内蒙包头人,副教授,硕士,从事工程力学教学工作。
U412
C
1008-3383(2017)05-0010-02
