多层叠合致密砂岩气藏产量劈分方法研究*

田　冷　申智强　刘　柳　王　猛

（1．中国石油大学石油工程教育部重点实验室2．中国石油大学（北京）石油工程学院）

多层叠合致密砂岩气藏产量劈分方法研究*

田冷1，2申智强1，2刘柳1，2王猛1，2

（1．中国石油大学石油工程教育部重点实验室2．中国石油大学（北京）石油工程学院）

多层叠合致密气藏产量劈分一直是制约产能评价的难题。基于动态生产特征分析，利用突变理论建立了多层叠合致密气藏产量劈分模型，形成了产量劈分的适用方法；应用该模型计算各层位的产量劈分系数，产量劈分系数是多层叠合致密气藏动态分析的关键参数之一，根据产量劈分系数计算出单井各产层的产量。其计算结果与实际产气剖面测试结果对比表明，该模型的计算结果是准确可靠的。产量劈分系数方法在多层叠合致密气藏的动态分析上具有推广价值，对生产措施的制定也具有参考作用。图3表5参9

致密气藏多层叠合产量劈分劈分产数动态分析

0　前言

多层叠合致密气藏开发的最大特点是多层合采［1］，其动态分析的最大难点也恰恰在于分层评价动态参数，即各产层的产量、动用储量及其采出程度、泄流半径等。现场收集到的动态数据日产气量、油压、套压等数据均为井口参数，即多层统筹数据。通过建立多层气藏产量劈分模型确定合采井各贡献层的劈分系数，计算各产层的产量，在此基础上对各主力层动静储量的采出程度和泄流半径进行评价。

常规的多层气藏产量劈分方法有有效厚度法、地层系数法、数值模拟法等，前两者考虑因素单一，仅考虑到静态参数，数值模拟法需要建立整个研究区三维模型，并进行复杂的历史拟合，多解性强，需要资料繁杂。

综合考虑多种因素，包括地质因素中的气层中深、气层厚度、孔隙度、含气饱和度、砂岩含量、密度、沉积微相，动态因素中的渗透率、层间干扰、压力，总计10个因素，通过运用数学拓扑学发展而来的突变理论建立了多层叠合致密气藏产量劈分新模型。并运用该方法对研究区统3井区合采井的各产层产量劈分系数进行了计算［2-3］。

1　突变理论

突变理论是由法国数学家伦尼汤姆于20世纪70年代创立，是一门综合运用拓扑学、奇点理论和结构稳定性研究内部作用不确定系统突变现象的数学学科，也可进行具有相同影响因素的不同物质的排序优选，其包括折叠突变、尖点突变、燕尾突变、椭圆脐突变、双曲突变、蝴蝶突变、抛物突变7种突变模型［4］。

应用最广泛的突变类型包括尖点突变、燕尾突变和蝴蝶突变模型［5］，其势函数和分歧点集方程见表1。

通过分歧点集方程可以导出归一公式，进而可求出系统总突变隶属函数值，因此归一公式中状态变量和控制变量需要归一到0～1之间。上述3种常用突变模型的归一公式如下：

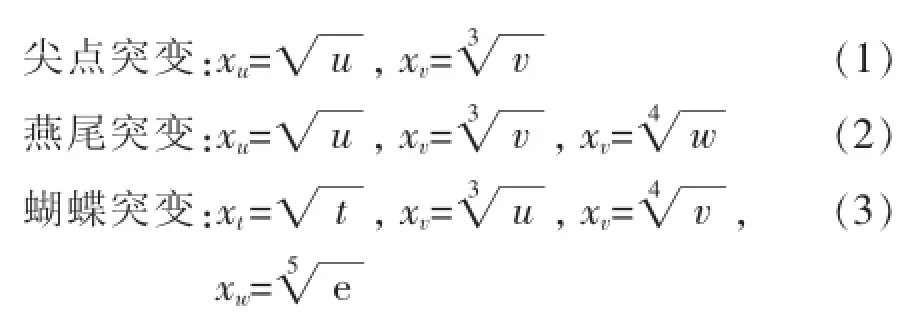
首先确定影响突变模型的控制变量，并进行影响大小排序和分类，建立由下到上，即指标层到准则层再到目标层的突变模型架构；对各控制变量进行归一化处理（数值范围为0～1，并且值越大越优）；根据架构内各层满足的突变模型，分别计算突变隶属函数值，最终求出不同评价对象的系统目标值。

2　计算方法

根据层次分析法的基本原理，综合考虑影响多层合采井各产层产量的有效厚度、孔隙度、含气饱和度、渗透率、层间干扰系数、气层中深压力、沉积微相、砂岩（白云岩）含量、储层密度和气层中深等因素，上述因素构成指标层；并对上述指标分为储量特征、开发特征、地质特征三类，构成准则层，最终构成产量劈分突变指标体系（图1）；根据控制变量个数确定相应的突变模型，建立突变模型架构（图2）。

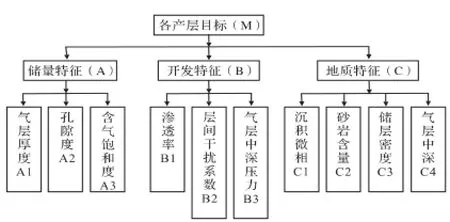
图1　产量劈分突变指标体系示意图

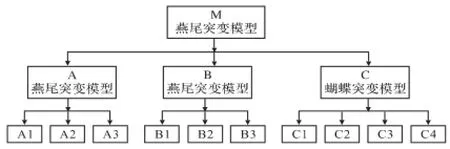
图2　突变模型架构图

系统突变隶属函数值的计算，需要对所有控制变量，即指标值进行无量纲归一化处理，公式如下：

当指标值对系统有利时xi为指标值，ci为各系统某指标所有样本的最大值；当指标值对系统不利时，xi为指标值倒数，ci为各系统某指标所有样本倒数的最大值。选取系统中各指标所有样本里对系统最不利的值组合相对突变面（表2），以进行后期的产量劈分系数计算。

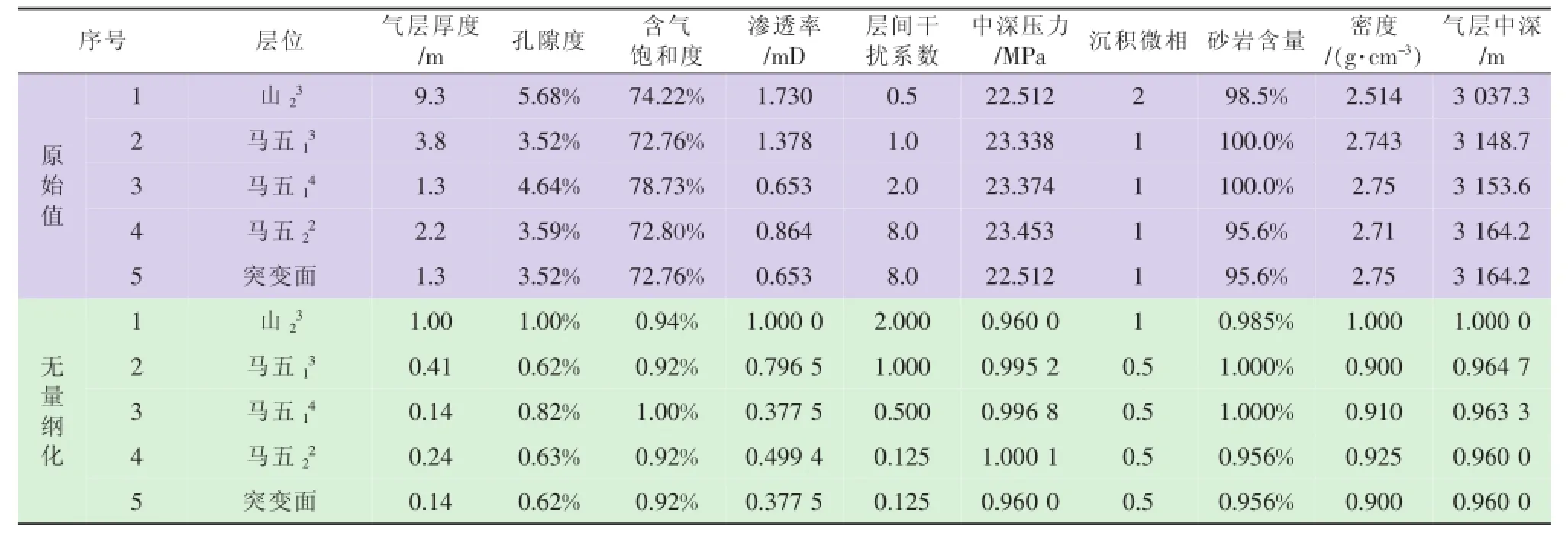
表2　Y29-0井控制变量指标值统计表

以相对突变面为例（图2），指标值气层厚度（A1）、孔隙度（A2）、含气饱和度（A3）构成燕尾突变模型，根据式（2）计算：

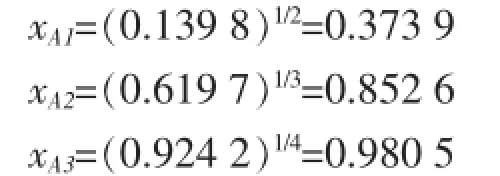
因此，A=（xA1+xA2+xA3）/3=0.735 6。

该层B1、B2、B3构成燕尾突变，同上计算得B= 0.701 4；C1、C2、C3、C4构成蝴蝶突变，同上计算C= 0.903 3。准则层构成燕尾突变，因此相对突变面产层系统目标值M=0.907 0。采用同样的方法，求得Y29－0井各产层的系统目标值，详见表3。

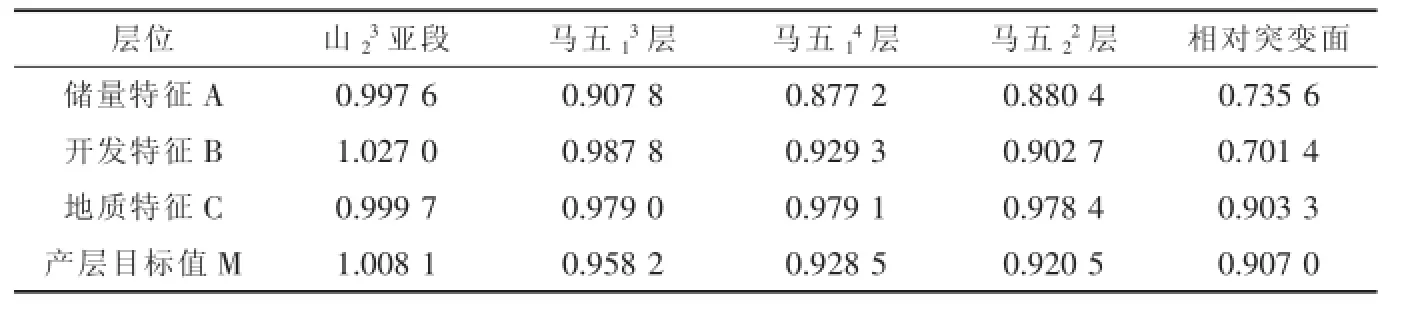
表3　YY29-0井各产层系统目标值

以Y29－0井山23为例，产量劈分系数计算公式如下：

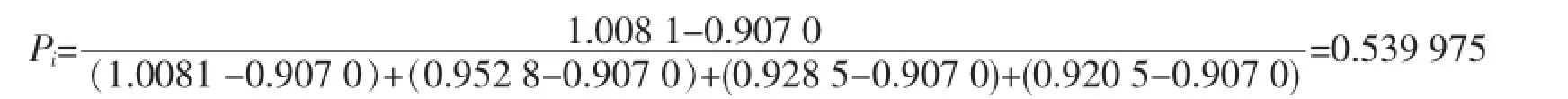
式中：

i—第i层；

n—为合采个数；

M'—相对突变面产层目标值。

同理计算出Y29-0井其他各产层的产量劈分系数；再通过传统的KH法计算产量劈分系数。该井在2006年6月25日进行了分层产气剖面测试，对比三种方法的测试结果，用突变理论求出的产量劈分系数较KH法要更加接近实际产气剖面测试结果，其劈分结果更加准确可靠。因此采用新建立的产量劈分模型对合采井的产量进行劈分（图3、表4）。

根据新建立的多层叠合致密气藏产量劈分模型，对研究区内19口生产井中的11口合采井进行了累产气量劈分系数的计算，并相应的计算了19口井各产层的产量贡献（表5）。

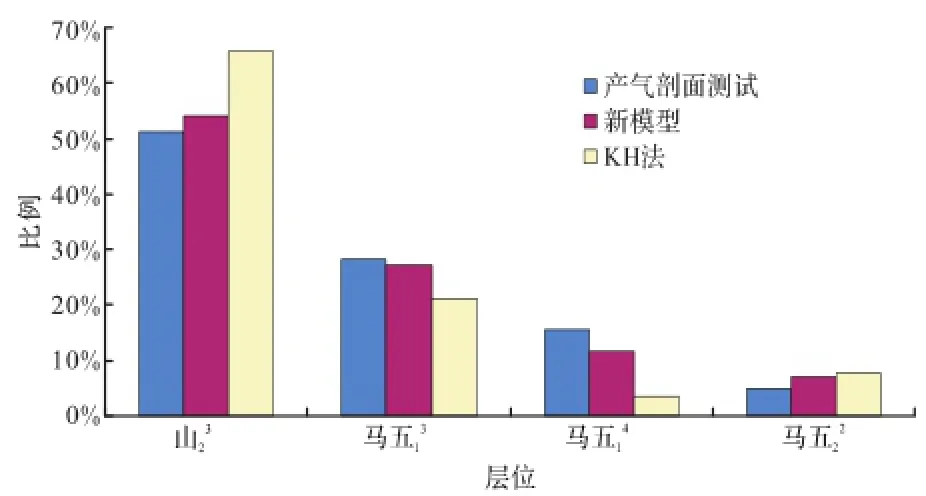
图3　新模型产量劈分系数对比图

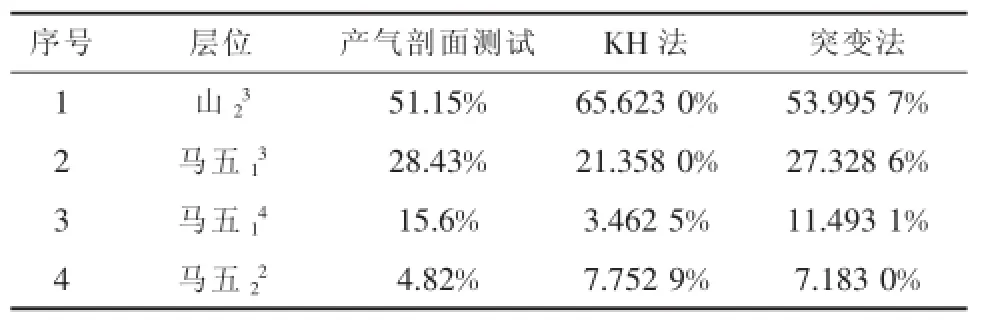
表4　Y29-0井不同计算方法得出的产量劈分结果

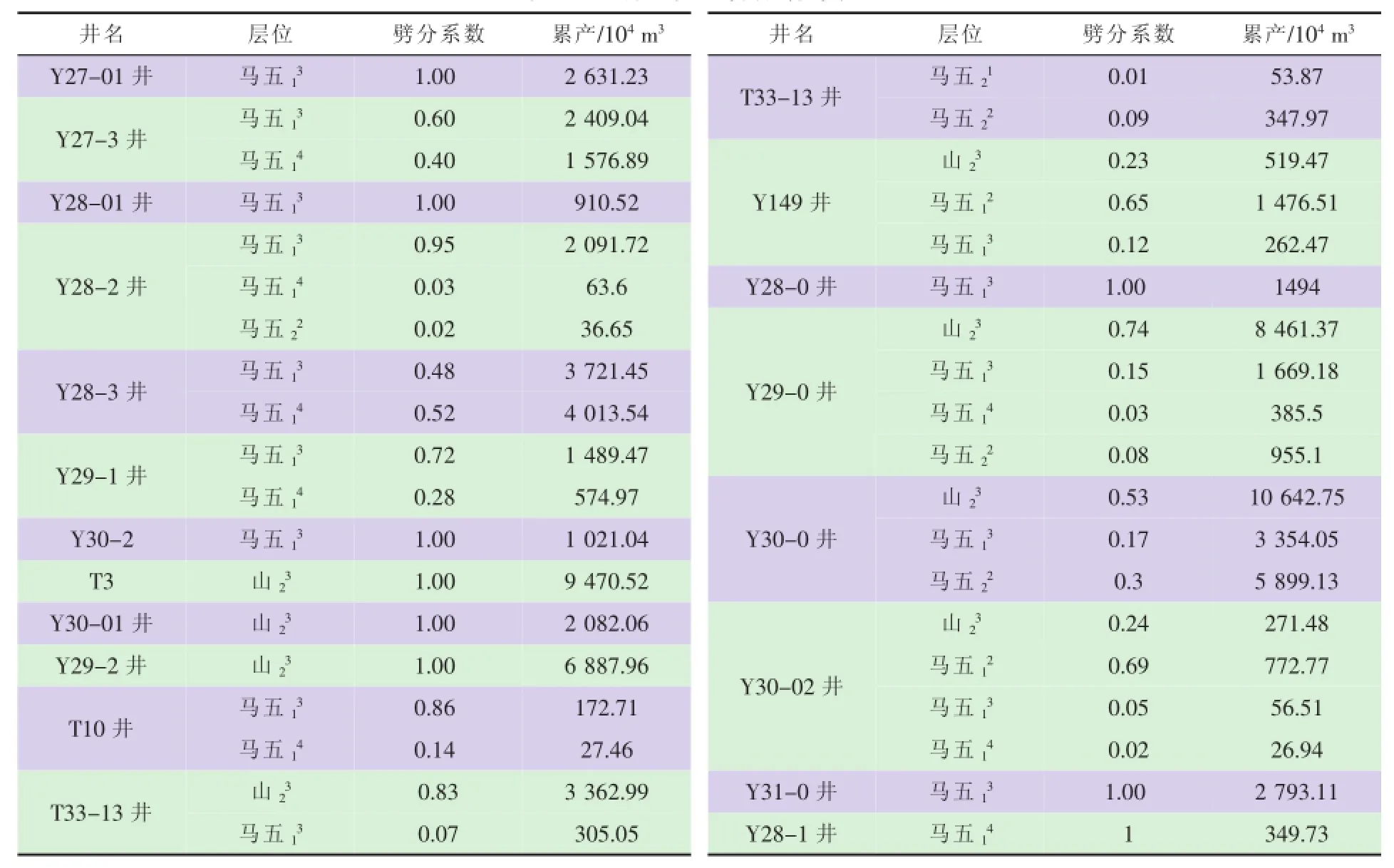
表5　T3井区产量劈分统计表

3　实例验证

以T3井区Y30-0井为例，该井同时射开山23亚段、马五13、马五22小层3套气层，日产量3×104m3以上，是该井区一口高产井，2005年12月投产。

该井先后进行过两次产出剖面测试（表6），两次测试时间分别是2007年3月和2010年6月。第一次产出剖面测试的结果为：山23产量所占百分比为59.1%，马五13产量所占百分比为20.7%，马五22产量所占百分比为20.2%；第二次产出剖面测试的结果为：山23产量所占百分比为55.6%，马五13产量所占百分比为19.7%，马五22产量所占百分比为24.7%。根据新建立的多层叠合致密气藏产量劈分模型，计算出Y30-0井各产层的产量贡献（表6），计算结果显示新模型计算结果与产出剖面测试结果基本一致，表明本方法准确可靠。

表6　产出剖面的测量时间及各层产量所占百分比统计表

4　结论

（1）通过突变理论建立了多层气藏产量劈分新模型，应用该模型求出了各层位的产量劈分系数，其较KH法要更加接近实际产气剖面测试结果，其劈分结果更加准确可靠；

（2）根据新建立的多层叠合致密气藏产量劈分模型，对研究区内生产井中的合采井进行了产量劈分系数的计算，根据计算得到的产量劈分系数，就可以计算出各产层的产量贡献。

［1］李敏，杨雅和.压力恢复资料计算低渗透气藏动态储量探讨［J］.天然气勘探与开发，1994，14（3）:36-38.

［2］刘启国，王辉，王瑞，等.多层气藏井分层产量贡献计算方法及影响因素［J］.西南石油大学学报，2010，32（1）:80-84.

［3］李幸运，郭建新.气藏储集层物性参数下限确定方法研究［J］.天然气勘探与开发，2008，31（4）:33-38.

［4］阚利岩，张建英，梁光迅，等.薄互层砂岩油藏产量劈分方法探讨［J］.特种油气藏，2002，9（5）:37-39.

［5］戴勇，李正文，吴大奎.突变论在地震资料储层预测中的应用［J］.天然气工业，2006，26（6）:47-49.

［6］孙文卿，冉茂云，熊建龙，等.突变理论在煤层气储层评价中的应用——以准格尔盆地砂沟井田为例［J］.天然气工业，2006，33（2）:28-21.

［7］郭金城，王怒涛.物质平衡与非稳态产能方程结合计算气井动态储量［J］.天然气勘探与开发，2010，33（4）:29-31.

［8］Blasingame TA，Lee WJ.Variable-rate Reservoir Limits Testing［C］//paper SPE 15028 presented at the Permian Basin Oil &Gas Recovery Conference of the Society of Petroleum Engineers，Midland，13-14 March，1986.

［9］Jorge A，Robert A.Production Analysis of Commingled Gas Reservoirs-CaseHistories［J］.2000，SPE 58985.

（修改回稿日期2016-07-28编辑文敏）

国家自然科学基金项目“基于声震效应的页岩储层多组分流体多场耦合流动机理”（U1562102）资助；2.中国石油大学（北京）基金项目（2462015YQ0218）“致密油气储层渗流特征研究”资助。

田冷，男，1977年出生，副教授；2006年博士毕业于中国石油大学（北京），现从事油气井测试技术和气藏工程教学与研究工作。地址（102249）：北京市昌平区中国石油大学石油工程学院。电话：（010）89733996、13401057612。E-mail：ltianshen@sina.com