卷烟主流烟气中相关成分测量不确定度评定的研究
2016-11-16王律陈贤飞王瑾姚蔚张宇张威冯群芝蔡悦秀
王律,陈贤飞,王瑾,姚蔚,张宇,张威,冯群芝,蔡悦秀
1 上海烟草集团有限责任公司,上海市杨浦区长阳路717号 200082;2 国家烟草质量监督检验中心,郑州高新技术产业开发区枫杨街2号 450001
烟草与烟气化学
卷烟主流烟气中相关成分测量不确定度评定的研究
王律1,陈贤飞1,王瑾1,姚蔚1,张宇1,张威2,冯群芝1,蔡悦秀1
1 上海烟草集团有限责任公司,上海市杨浦区长阳路717号 200082;2 国家烟草质量监督检验中心,郑州高新技术产业开发区枫杨街2号 450001
为研究卷烟主流烟气中相关成分测量不确定度评定方法、数据验证方法,以及不同样品和不同机型吸烟机测量不确定度,以氰化氢、氨、苯酚、巴豆醛、NNK和苯并[a]芘为目标物,选用GUM法并通过简化计算公式、讨论不确定度的主要来源及与输入量的关系建立测量模型,通过数据相关性探讨,计算合成标准不确定度和扩展不确定度。通过组织共同实验,以重复性限、再现性限验证数据的有效性。通过选取不同卷烟样品评定测量不确定度并回归拟合建立不同测量结果的测量不确定度估计值函数关系。通过拟合曲线置信区间验证不同机型吸烟机的测量不确定度。结果表明:①GUM法适用于卷烟主流烟气中相关成分测量不确定度评定,组间变异和组内变异是输入量c最大的权重分量,包含因子k=2的扩展不确定度与对应测量值的比值在6.2%~14.4%之间。②运用共同实验的重复性限、再现性限是验证数据的有效方法,并验证了本评定的数据都是有效的。③不同样品的测量值与测量不确定度有明显的相关性,可以通过函数关系式用测量值获取测量不确定度估计值。④不同机型吸烟机的测量结果和测量不确定度呈现一定差异,但不致显著影响测量不确定度估计。
卷烟;主流烟气;相关成分;测量不确定度
卷烟主流烟气中相关成分是指一氧化碳、氰化氢、氨、苯酚、巴豆醛、NNK和苯并[a]芘等7种代表性的卷烟烟气有害成分[1-2]。一氧化碳不在本文研究范围内。
测量不确定度是定量分析结果的重要组成部分,是评价分析结果可信度的重要参数[3-4]。推广和应用测量不确定度评定可以促进与先进实验室接轨,又可以消除国际技术壁垒、确保检测结果互认互信,也可以保持检测能力和保证实验室检测水平[5]。1993年,国际标准化组织(ISO)等7个国际组织制定了《测量不确定度表示指南》(GUM),以GUM为指导的不确定度评估得以大力推广[6-9]。我国1999年等效采用GUM,颁布了JJF 1059《测量不确定度评定与表示》,国内学者开始研究不确定度,涌现大量著述和文章[10-16]。
烟草行业测量不确定度评定近年发展较快。2007年以来先后发布了系列计量技术规范,发表了有关的文章[17-20],有一些涉及卷烟主流烟气中相关成分测量不确定度评定[21-27]。这些研究提升了测量不确定度评定的技术水平,但也存在局限性等问题:就计量技术规范而言,存在覆盖测量指标较少,以常规测量、常量指标为主,范围较窄。就已发文章而言,存在系统研究不多、基础研究较弱、拓展研究很少等问题。
本文以卷烟主流烟气中氰化氢、氨、苯酚、巴豆醛、NNK和苯并[a]芘为目标物,研究测量不确定度评定方法,主要方向有:测量模型建立中计算公式的简化和修正因子、输入量间的相关性、不确定度来源和权重分量。对评定数据有效性验证方法、不同释放量样品和不同机型吸烟机测量值与测量不确定度分别进行了研究。
1 材料与方法
1.1 材料、仪器和计量器具
测量不确定度评定和数据验证选用3R4F监控卷烟(NNK为某一中式卷烟)样品,拟合实验选用各6个卷烟样品,这些样品确保氰化氢在30.0~130.0μg/cig、氨在3.0~9.0μg/cig、苯酚在4.0~19.0μg/cig、巴豆醛在4.0~22.0μg/cig、NNK在5.0~16.0ng/cig、苯并[a]芘在4.0~13.0ng/cig的范围内,并尽可能呈现在范围内的等梯度差异。
Cerulean SM450吸烟机;Borgwaldt RM200A吸烟机;Bran-Luebbe AA3连续流动分析仪;Dionex ICS5000离子色谱仪;Agilent 1260液相色谱仪;Agilent 6460 液质联用仪;Agilent 5976C气质联用仪;Mettler Toledo XP404S电子天平。
定量加液器(计量证书附最大允差);移液枪(附最大相对允差);容量瓶(附最大允差)。
1.2 方法
1.2.1 测量不确定度评定
以氰化氢、氨、苯酚、巴豆醛、NNK和苯并[a]芘为目标物,按照检测依据建立测量过程,推导出计算公式并合并,简化。分析不确定度来源及与输入量关系,确定测量模型。评定不确定度分量和输入量间相关性,计算合成标准不确定度和扩展不确定度。
在分量评定中:1)不同时间段测量值变异分量以组间差估计值量化:重复测量,获取样品的浓度值;确认各平均值呈正态分布;异常值检验,剔除离群值;计算组间、组内偏差平方和及组间差的估计值。2)测量重复性分量以标准差的估计值量化:将极差转化为标准差。3)样品前处理和标准工作溶液配制分量用B类评定方法。4)仪器测量重复性用贝塞尔公式进行A类评定。
1.2.2 数据验证
组织烟草行业不同地域分布的9家实验室进行共同实验,实验方案与本评定方法一致,样品由本实验室统一随机分配。统计方法:1)对各实验室10组测量值进行异常值检验,剔除离群值。2)用曼德尔h检验各实验室测量均值,用曼德尔k检验各实验室测量精度,剔除离群值。3)计算重复性限r和再现性限R。检验方法:1)本实验室的10组测量值的极差<r ;2)本实验室的平均值与其他实验室平均值的最大、最小值的差值<R。如同时满足上述2个判则,方可确认评定中相应数据准确有效。
1.2.3 线性拟合
选取呈梯度的各6个卷烟样品进行测量不确定度评定,以测量结果和对应的不确定度进行线性拟合。若决定系数>0.85,接受拟合方程;否则以95%置信概率,建立拟合方程置信区间,剔除异常点,再次拟合和评价。
1.2.4 吸烟机机型验证
对苯酚、NNK和苯并[a]芘换成不同机型吸烟机抽吸,评定和计算合成标准不确定度,放入用原机型建立的线性函数的置信区间检验。
2 结果与讨论
2.1 测量模型
2.1.1 计算公式及简化
计算公式是由测量原理方法导出的,没有考虑不确定度评定的需要,但计算公式中对测量结果不确定度有影响的输入量必须要考虑[28]。经过对计算公式中常数、系数进行合并,简化,都可以简并为式(1)的形式,式(1)中c代表目标物浓度,V代表体积。

用内标法NNK、苯并[a]芘也可以进行类似简化,c代表目标物与内标质量比值的测量值,mis代表内标质量。见式(2):

2.1.2 输入量
建立测量模型先要考虑不确定度来源,这些来源作为不确定度测量模型的输入量。不确定度主要来源有10个[29]。本评定的被测量都有明确定义,使用成熟方法,测量仪器精度、灵敏度和检出限等都符合方法要求,检测结果都由色谱工作站等自动积分计算,不涉及人员读数偏移,所以文献[29]中来源a)被测量的定义不完全、b)被测量定义的复现不理想、c)取样代表性不够、e)模拟式仪器的人员读数偏移、h)引用常数或其他参数值的不准确和i)测量方法和测量程序中的近似和假设等6个方面不予考虑。本评定从来源d)环境条件影响、f)测量仪器性能、g)标准物质的标准值、j)测量重复性等4个方面考虑。
化学测量影响来源较多,会导致复杂函数关系的测量模型,甚至不能表示为显式,在确定各输入量的相关性时会导致关系不清和难度增加等问题。简单的测量模型,通常是指计算公式加修正值和(或)乘以修正因子,甚至就是计算公式[28]。基于此,也基于计算公式简化结果,选用简单测量模型的策略:即简化成Y=X1+X2或Y=X1×X2。是否可行,还要解决2个问题:一是不确定度来源与输入量关系;二是修正值或修正因子。
因果关系图可以识别不确定度来源,表述不确定度分量与输入量、分量与分量之间的关系。图1以氨为例,可见浓度测量结果、体积的各个不确定度来源。其他目标物与其相似(苯酚、巴豆醛)或类同(氰化氢气相或粒相单个部分是相似的;NNK和苯并[a]芘是内标法,将浓度测量结果改为目标物质量与内标质量的比值、将体积改为内标质量)。在本评定中,予以考虑的不确定度来源与输入量对应明确,不另增输入量。
本评定以加标回收率衡量测量误差。标准中以及本实验室的加标回收率结果在95%~110%,对于微量、痕量水平的测量,AOAC对该水平浓度平均回收率的要求为80%~110%,是可以接受的[30-31]。本评定不对计算公式加修正值或修正因子。
2.2 评定方法选择
GUM法[29]和蒙特卡洛法(MCM法)[32]是测量不确定度评定的2种主流方法。GUM法在涉及有明确定义的、并可用唯一值表征的被测量估计值的不确定度时,可被优先选用。选用GUM法或MCM法评定测量不确定度还有3种适用情况:

图1 因果关系图Fig. 1 Cause-effect diagram

表1 2种评定法的适用情况Tab. 1 Applicable conditions for two estimation methods
本评定被测量是明确定义并用唯一值进行表征,测量模型都是线性的。输入量V或mis的各分量都是对称分布,因此判断V或mis应是对称分布;输入量c的概率分布未知,对c的测量结果用夏皮罗-威尔逊检验法进行正态性检验(m=10),结果见表2。

表2 输入量c的正态性检验结果Tab. 2 Normal test results of input c
取α=0.05,临界值W(10,0.05)=0.842,表2中W>W(m,α),所以c的概率分布都为正态(对称)分布。V或mis是固定值,输出量取决于c,其分布与c是同分布;而氰化氢的气相和粒相释放量都是正态分布,两个正态分布相加的结果不一定是正态的,需正态性检验:W=0.8853,W>W(m,α),所以氰化氢输出量也是正态分布。本评定符合GUM法的主要适用条件,选择GUM法是适宜的。
2.3 不确定度因素
各目标物的测量原理、过程和测量模型类似,不确定度因素也类似,以氨为例。1)不同时间段测量值变异引入的不确定因素:主要包括吸烟机参数的变异、环境条件的变异等形成测量结果的变异,具体体现是不同时间段各组间测量结果的变异。2)测量重复性引入的不确定因素:第一测量结果由2个平行的平均值获取,平行测量数据间的差异形成了测量结果的变异。3)样品的前处理引入的不确定因素(也是构成体积变异的因素):气相收集定容不准、粒相收集加液不准形成的变异。4)标准溶液制备引入的不确定因素:在系列标准溶液制备中,各计量器具不准产生的变异。5)离子色谱法引入的不确定因素:拟合工作曲线非线性形成的变异。6)仪器测量重复性引入的不确定因素:离子色谱仪测量稳定性形成的变异。
其他目标物不确定度因素不同之处主要有:由于测量过程差异,氰化氢有气相和粒相2部分组成;由于测量方法差异,NNK、苯并[a]芘用内标法,mis为内标质量的变异。
2.4 不确定度分量评定
2.4.1 不同时间段测量值变异

表3 氨浓度值Tab. 3 Concentration of ammonia μg/(mL·cig)
组间差估计值的获取是建立在χ2分布基础上,前提是数据服从正态分布。正态性检验结果W=0.9765,大于临界值。格拉布斯检验结果是没有异常值。
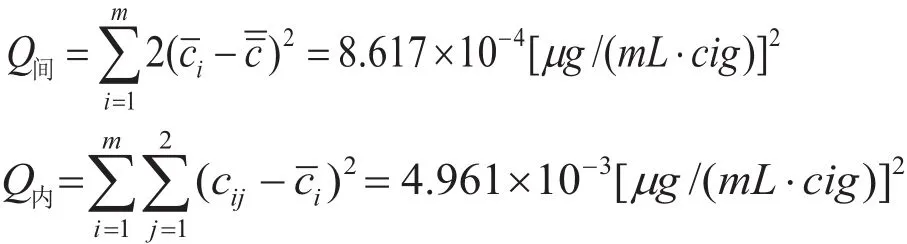
计算组间差的估计值,在正态分布的基础上:

平行测量2次,将n=2代入,可以得公式(5)、(6):

2.4.2 测量重复性

式(8)中:1.128是n=2时极差转化为标准差的系数查表值。
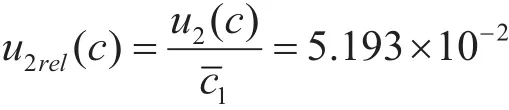
2.4.3 样品的前处理
样品前处理主要受定量加液器、移液枪和容量瓶校准及各液体温度的影响。
(1)校准
校准的信息由计量证书等资料提供,可能提供的是最大相对允差(Dr),或是不确定度(uc)。urel(qdc)分别可以用式(9)、(10)评定(三角分布)。

如未获取到资料,可设计重复性实验,参照贝塞尔公式进行A类评定。连续称量定量加液器移取水的质量,用密度转换。见式(11)。这种评定方式是假设了天平的精度足够高、测量过程等足以保证引入的不确定度相对于水质量是足够小,也适用其他量具,如容量瓶、移液管等。
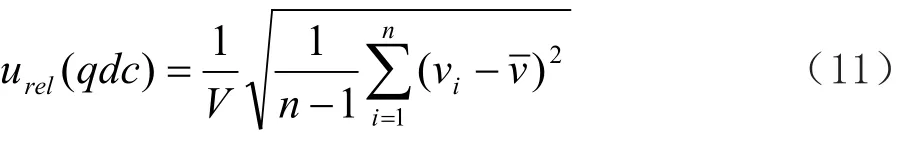
(2)温度
溶液有体膨胀特性,须考虑温度变化形成的不确定度。计量器具一般在20℃检定,实验室温度一般在(20±5)℃,按均匀分布考虑。则其相对不确定度urel(qdt)见式(12),αv是液体的体膨胀系数。

(3)分量合成
按互不相关进行合成,得气相吸收液定容的相对不确定度。同样评定移液管和容量瓶,得到粒相萃取液定容的相对不确定度,合并定容时的相对不确定度;对三者按互不相关合成即得样品前处理分量的不确定度。
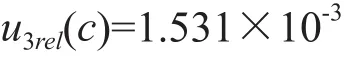
2.4.4 标准溶液制备引入的不确定因素
(1)标准物质纯度
标准物质或参考标准物质提供了不确定度及相应信息,直接引用或将扩展不确定度除以包含因子转化为标准不确定度即可。参考标准物质和作为标准品使用的化学试剂,可以用证书给出的纯度或浓度的最大允差,按照均匀分布评定。
(2)标准物质称量
标准物质是固态的,会使用天平。计量证书给出不确定度信息,直接引用。如给出的是最大允差,按照均匀分布考虑;一般还要考虑分辨力,特别是称量标准品时,称量物的质量较小。按照式(13)、(14)分别计算最大允差引入的不确定度分量urel(be)和分辨力引入的不确定度分量urel(br),再按互不相关合成。

检测实验室一般不考虑砝码校准、温度、空气浮力等因素的影响。评定中还须注意几个问题:1)不管是容器先称量再加被称量物品称量,或者容器先在天平置零再称被称量物品,都是2次称量。2)公式中m不是被称量物品的质量,都是“毛重”,是容器加上被称量物品的质量,在容器质量远大于标准品质量时,才可以将质量视作相同。
(3)标准储备液体积
如果标准物质是固态的,还会使用容量瓶定容,其评定方法与2.4.3类似。
(4)标准储备液不确定度
标准物质纯度、标准物质称量和容量瓶定容3者间互不相关合成标准储备液的相对不确定度urel(ss)。
(5)标准储备液稀释定容
涉及用移液管或移液枪定量移取标准储备液和用容量瓶体积定容,可分别评定后,按互不相关合成稀释定容的相对不确定度urel(d)。
(6)按照式(15)合成标准溶液制备引入不确定度分量urel(ws),即u4rel(c)。
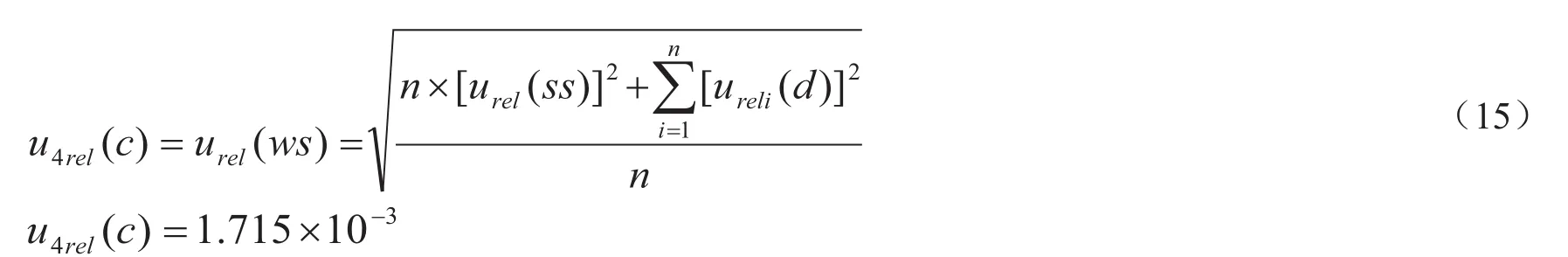
2.4.5 离子色谱法
最小二乘法拟合标准曲线,其不确定度u5rel(c)按式(16)计算[33]。

2.4.6 离子色谱仪测量重复性
同一样品连续进样n次,测量重复性不确定度u6rel(c)按照贝塞尔公式计算。
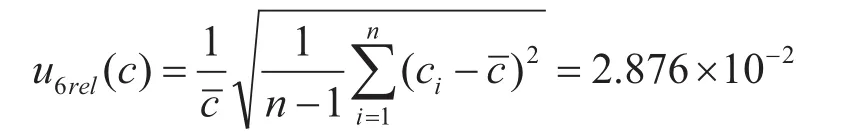
2.4.7 体积变异
体积变异的不确定因素与浓度测量值中样品的前处理完全一致。
2.4.8 其他问题
(1)氰化氢的气相、粒相是分别测量的,但分量评定类似。
(2)各指标的标准工作溶液制备级数不同,评定时可将上一级的储备液视作标准储备液,下一级的标准储备液视作标准工作溶液。
(3)内标法涉及计量器具的评定中,须将质量的影响转为体积的影响后再行评定,还需识别目标物与内标质量比c与部分量具是否有有关。比如,虽然测量方法要求以容量瓶定容,但目标物和内标在同一容器内被同倍浓缩或稀释了,定容不准确却不影响质量比。内标的加入方式(加入在萃取液中或是前处理过程中加入)也会导致评定的不同。比如NNK测量过程中是用加入内标的萃取溶剂进行萃取,内标质量的评定相同;但苯并[a]芘是萃取、纯化、浓缩后加入,内标质量实质上是前处理分量的一部分。
2.5 分量权重比较
由于2个输入量中,V或mis的权重明显都小于c,讨论c的分量才有意义。见图2。

图2 输入量c的不确定度分量Fig. 2 Uncertainty components of inputs c
以最大分量为基准,将大于其1/3作为权重分量。各输入量c中,有2到4个,权重分量多少反映了主要影响因素的集中程度:氰化氢粒相和苯酚主要影响因素相对集中,而氨、NNK和苯并[a]芘相对分散。
2.5.1 组间变异u1rel(c)和组内变异u2rel(c)
u1rel(c)、u2rel(c)都出现了,且排序靠前(除了氨),说明组间变异和组内变异对输入量c的影响都较大。还出现一个规律:u1rel(c)似略大于u2rel(c),且出现在目标物在粒相中的项目。为考察假设,增加了5个量值呈一定梯度的样品进行测量不确定度分量评定。以作为统计量,并将M≥10%视作显著。见图3。
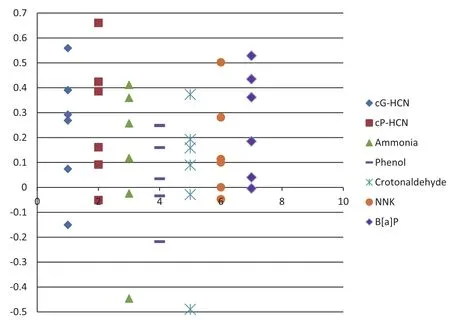
图3 统计量M高低分布图Fig. 3 High-low distribution diagram of statistics M
总体上组间变异略大于组内变异,但分散性较大;这个现象与目标物存在相态无关。吸烟机参数(风速、抽吸容量)、孔道间差异和实验室环境(温度、相对湿度)的变异,以及样品的不均匀、收集目标物可能的偶然误差等,都影响了组间、组内变异。
2.5.2 标准溶液制备u4rel(c)
量级都在10-3,只在巴豆醛和NNK中是权重分量,也是权重分量中较小的。在标准工作溶液个数要求基本相同情况下,内标法同时需对内标溶液移取或稀释定容,相对外标法不确定度分量要大;标准储备液的级数是最重要的原因。能加以控制的,可从标准品选择等方面考虑:比如尽量使用液体标准物质,减少称量和第一级标准储备液的配制,配置量程和精度适宜的计量器具,控制温度等。
2.5.3 拟合曲线u5rel(c)
成为权重分量概率不低,在都用最小二乘法拟合、标准工作溶液个数基本相同、都以2平行出具测量结果的前提下,分量的大小取决于拟合曲线的线性(SE是主因)、样品与标准工作溶液中心点的距离等。某些报道中,先期就假设标准工作溶液配制相对于标准工作曲线拟合非线性是极小的而不予考虑,实际上并非都适用,比如在巴豆醛和NNK中 2个分量就相差不多。所以在未取得确实证据的情况下,单纯通过假设就忽略影响存在很大风险,特别是标准物质纯度不确定度相对较大、标准储备液级数较多等情况下,一定要对其评估。另外,为降低工作曲线拟合的不确定度分量而故意增加标准工作溶液的个数很可能会得不偿失,因为降低此部分的同时标准工作溶液部分的不确定度分量增加了,当然首先是这两者都必须是权重分量。
2.5.4 仪器测量重复性u6rel(c)
离子色谱仪测量的氨、气相色谱-质谱联用仪测量的苯并[a]芘中出现该权重分量,在其他5个卷烟样品也复现了这种现象。
2.6 标准不确定度和扩展不确定度
在合成标准不确定度前,要对相关性进行分析。各目标物完成收集后,容器内目标物的量是恒定的,可以在微小区间内确定c和V(或mis)的相关系数。见表5。
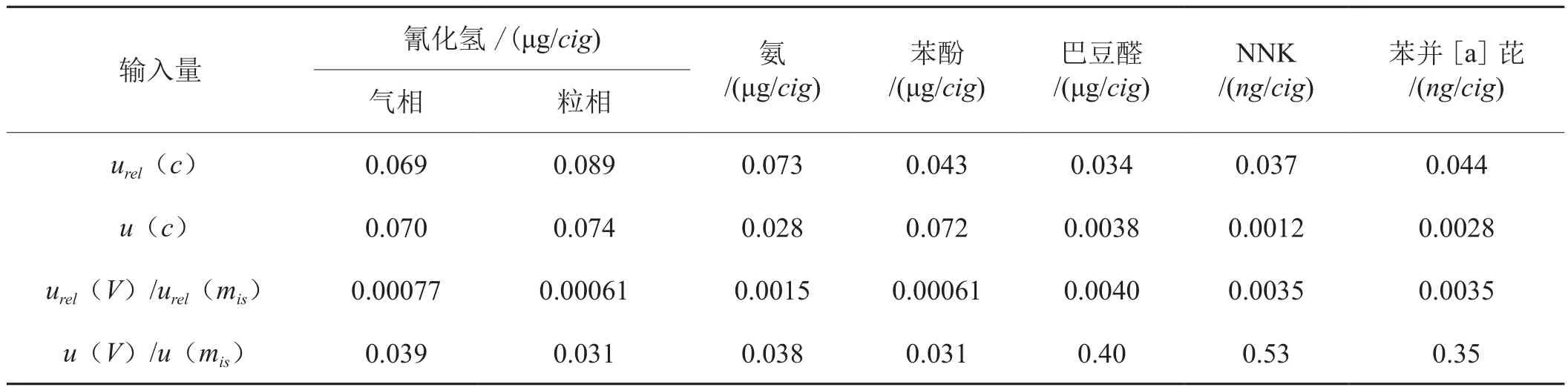
表4 各输入量的相对不确定度和不确定度Tab. 4 Relative uncertainty and uncertainty of each input

表5 各目标物输入量相关系数Tab. 5 Correlation coef fi cient of each object’s input
由于各相关系数都显示2个输入量间呈强负相关,在合成标准不确定度时确实应该将两者的相关性予以考虑。
简单测量模型在合成标准不确定度时体现了其优点:即使存在相关性,用通用公式也可以比较简便地计算。由于N=2(2个输入量),将2个输入量、相关系数代入通用公式[29],得式(17):

根据测量模型y=c×V可得:。各项相关系数都非常接近-1,化简后都可以得到类似式(18)形式:


表6 各目标物的合成标准不确定度Tab. 6 Combined standard uncertainty of each object
还需对yHCN进行合成。先对yG和yP的相关性进行检验。选用6个样品分别进行10组测量,相关系数见表7。

表7 氰化氢气相与粒相测量值的相关系数Tab. 7 Correlation coef fi cient of the measurements of HCN gas phase and particle phase
当n=20,取α=0.05,|r临界|=0.444。除6#样品具有一定的相关性外,其余均不相关,故应视r(yG,yp)=0。
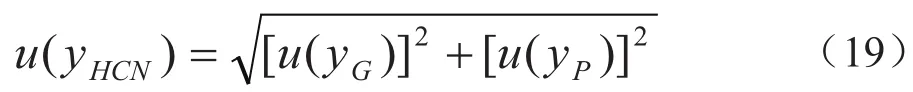
对于检测实验室,扩展不确定度一般情况下可取k=2,表述为U=2u(y)。

表8 各目标物的扩展不确定度Tab. 8 Expansion uncertainty of each object
2.7 检测数据验证
本实验室的结果同时满足了2个判则,数据准确性和精度都有保证,验证了在测量不确定度评定中的数据是有效的。
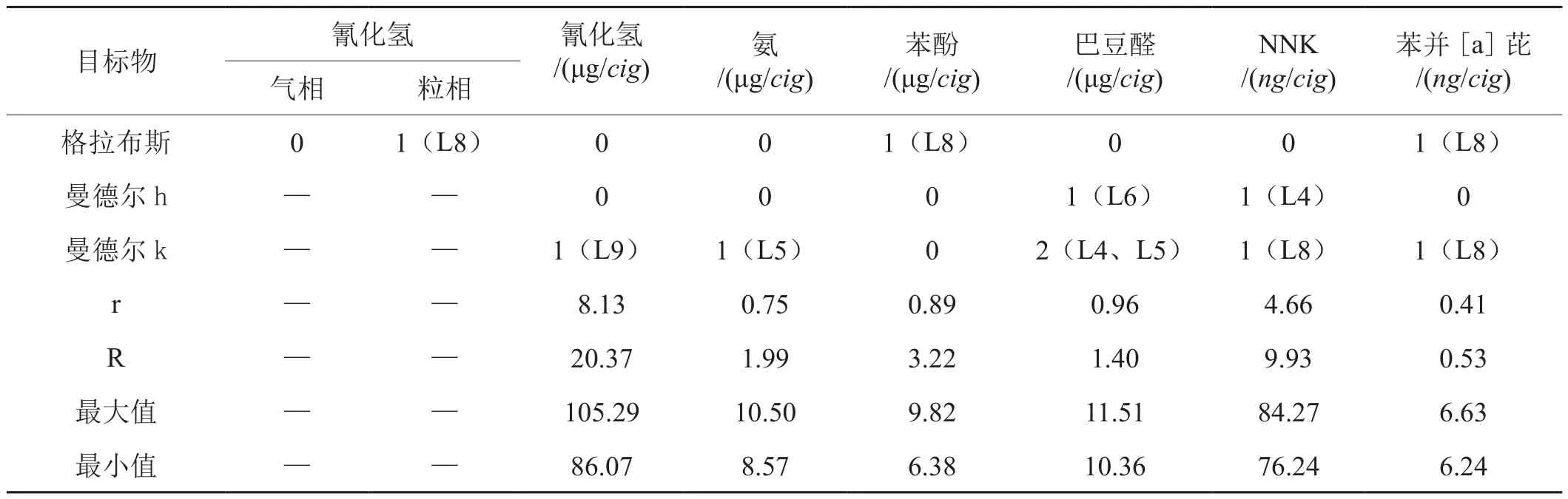
表9 检验和统计结果Tab. 9 Test and statistics results
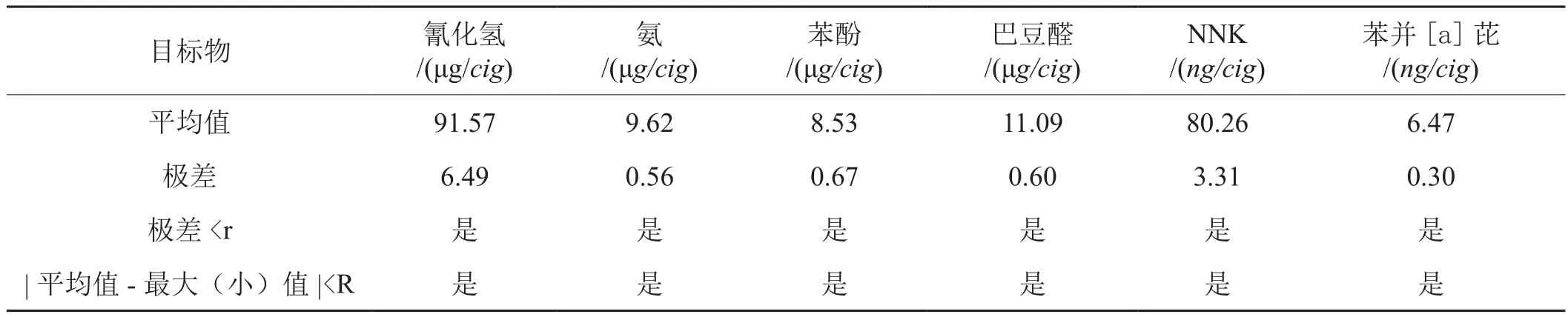
表10 统计和判定结果Tab. 10 Statistics and determination results
2.8 测量不确定度的梯度拟合和应用


图4 线性拟合图Fig. 4 Linear fi tting diagram
从图4可见:氰化氢、氨、巴豆醛和NNK线性较好;但在NNK中,由于其中一点(3R4F监控卷烟)与总体测量结果在量值上相距甚远,使用此拟合线可能存在很大的风险,决定剔除此点。苯酚和苯并[a]芘的拟合线性未满足要求,某些点明显偏离总体在拟合线的95%置信区间外。
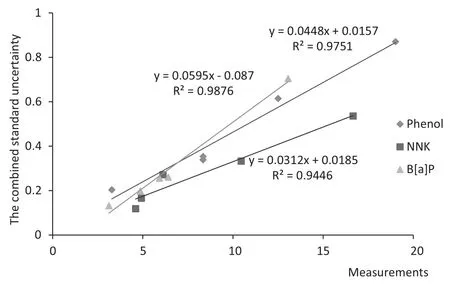
图5 剔除点后线性拟合图Fig. 5 Linear fi tting diagram after point deletion
图5为剔除点后的线性拟合图,决定系数都满足要求;NNK适用范围缩小后对一般的中式卷烟样品都是适用的。
通过函数关系可以在获得测量值的情况下,简便地估计测量不确定度,避免大量实验工作和计算,在本实验室中具有非常大的价值。对于用标准方法开展测量的其他实验室,也具有一定的参考意义,拓展了应用范围。

表11 测量值和合成标准不确定度的函数和相关系数Tab. 11 Function and correlation coef fi cient of the measured value and the combined standard uncertainty
2.9 不同机型吸烟机检验
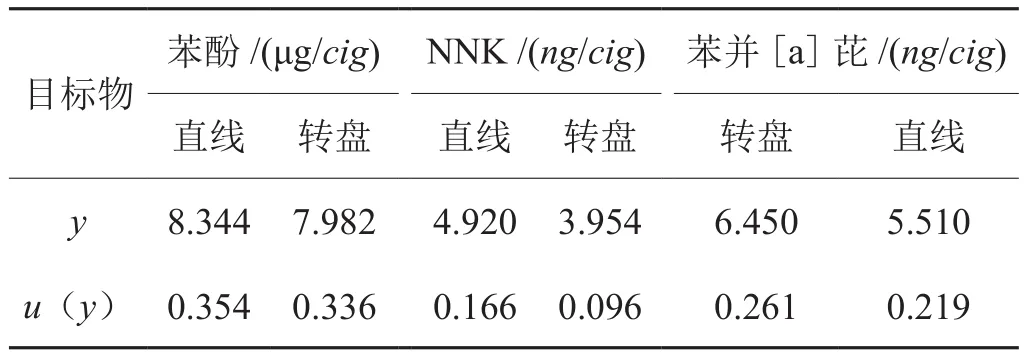
表12 不同机型吸烟机测量值和合成标准不确定度Tab. 12 Measurement value and the combined standard uncertainty of different smoking machine models
表12显示了苯酚、NNK和苯并[a]芘的转盘型吸烟机与直线型吸烟机测量值和合成标准不确定度存在一定的差异。图6展示了显著差异检验的结果,从图上可以看出这些点仍包含在用原机型的函数置信区间以内,说明吸烟机机型并非影响3个卷烟主流烟气相关成分测量不确定度的关键因素,也证明了建立的测量不确定度函数也同样适用于不同机型吸烟机测量结果推测相应的合成标准不确定度,在应用上具有一定的通用性。

图6 不同机型吸烟机验证图Fig. 6 Veri fi ed diagram of different smoking machine models
3 结论
本文选用GUM法建立了卷烟主流烟气中相关成分的测量不确定度评定方法,给出权重分量;提供一种测量不确定度中确认数据有效性的方法,并通过拟合曲线的分析,给出对应于测量结果的测量不确定度估计值。
(1)GUM法适用于卷烟主流烟气中相关成分测量不确定度评定,对于化学测量,在评定中简化计算公式建立测量模型和考虑相关性是必要的;组间变异和组内变异是输入量c最大的权重分量;包含因子k=2的扩展不确定度与对应测量值的比值在6.2%~14.4%之间。
(2)共同实验的重复性限和再现性限是验证数据的有效方法。用该方法验证,本评定的数据都是有效的。
(3)不同样品的测量值与测量不确定度有明显的相关性,在适用范围内可以通过函数关系式用测量值获取测量不确定度的估计值。
(4)不同机型吸烟机的测量结果和测量不确定度呈现一定差异,但不致显著影响测量不确定度估计。
[1] 谢剑平.烟草与烟气化学成分[M].化学工业出版社,2010:28-57.Xie Jianping. Tobacco and chemical composition of smoke[M].Chemical Industry Press,2010:28-57. (in Chinese)
[2] 谢剑平,刘惠民,朱茂祥,等.卷烟烟气危害性指数研究 [J].烟草科技,2009,(2):5-15.Xie Jianping, Liu Huimin, Zhu Maoxian, et al. Development of a novel hazard index of mainstream cigarette smoke and its application on risk evaluation of cigarette products[J]. Tobacco Science & Technology, 2009,(2):5-15. (in Chinese)
[3] 马俊英.测量不确定度评定在计量检定中的应用[J].中国质量技术监督,2013,(12):66-67.Ma Junying. Application of measurement uncertainty evaluation in metrology and verification [J].China Quality Supervision, 2013,(12):66-67. (in Chinese)
[4] 祝海林,邹旻.测试数据的处理与不确定度评定[J].计量与测试技术,2000,(6):34-36.Zhu Hailin,Zou Min. Data process and determination of uncertainty in measurement[J]. Metrlogy and Measurement Technique,2000,(6):34-36. (in Chinese)
[5] 田芳宁. 实验室认可中的测量不确定度评定[D].合肥工业大学,2012:1-8.Tian Fangning. Measurement uncertainty evaluation in calibration laboratory accreditation[D].Hefei University of Technology,2012:1-8. (in Chinese)
[6] BIPM, ISO. Guide to the Expression of Uncertainty in Measurement. Geneve: ISO,1995.
[7] Ellison S L R, Rosslein M, Williams A. Quantifying uncertainty in analytical measurement. 2nd ed. UK: EURACHEM /CITAC, 2000.
[8] Max R. APLAC interpretation and guidance on the estimation of uncertainty of measurement in testing [J]. J AOAC international, 2003, 86(5): 1070-1076.
[9] Silva GMS. Uncertainty of analytical determination[J]. J AOAC international, 2003, 86(5):1077-1184.
[10] 刘智敏.不确定度与分布合成[J].物理实验,1999,19(5):17-19.Liu Zhimin. Uncertainty and distribution synthesis[J]. Physics Experimentation, 1999, 19(5): 17-19. (in Chinese)
[11] 刘智敏. 测量不确定度及其应用[J]. 计量技术,2001,(6):46-49.Liu Zhimin. Measurement uncertainty and its application[J].Measurement Technique, 2001, (6): 46-49. (in Chinese)
[12] 刘智敏. 扩展不确定度的新算法[J]. 中国计量学院学报,2003,14(1):3-12.Liu Zhimin. New method for calculating expanded uncertainty[J]. Journal of China Institute of Metrology, 2003,14(1): 3-12. (in Chinese)
[13] 张海滨,王中宇,刘智敏. 测量不确定度评定的验证研究[J].计量学报, 2007, 28(3): 193-197.Zhang Haibin, Wang Zhongyu, Liu Zhimin. On the veri fi cation of measurement uncetainty[J]. Acta Metrologica Sinica, 2007,28(3): 193-197. (in Chinese)
[14] 刘智敏. 分布传播及其在不确定度中的应用[J]. 中国计量学院学报,2008,19(1):1-9.Liu Zhimin. Propagation of distributions and its application on uncertainty[J]. Journal of China Jiliang University, 2008,19(1):1-9. (in Chinese)
[15] 尚德军,王军.测量不确定度的研究和应用进展[J].理化检验-化学分册,2004,40 (10):623-627.Shang Dejun, Wang Jun. Development and application of the expression of uncertainty in measurements[J]. Physical Testing and Chemical Analysis Part B Chemical Analysis,2004,40(10):623-627. (in Chinese)
[16] 刘建坤,朱家平,郑荣华. 测量不确定度评定研究现状及进展[J]. 现代科学仪器,2013,(5):12-17.Liu Jiankun, Zhu Jiapinp, Zheng Ronghua. Research status and development of evaluation of measurement uncertainty[J].Modern Scienti fi c Instruments,2013,(5):12-17. (in Chinese)
[17] 李海燕,肖燕,潘丽萍,等. 卷烟吸阻测量不确定度的评定[J]. 烟草科技,2004,(2) :36-37.Li Haiyan, Xiao Yan, Pan Liping,et al. Uncertainty in measurement of cigarette draw resistance[J]. Tobacco Science& Technology, 2004,(2): 36-37. (in Chinese)
[18] 李恩增,沈凤兰,张薇. 焦油量测定结果的不确定度评定[J].现代测量与实验室管理,2003,(6): 37-40.Li Enzeng, Shen Fenglan, Zhang Wei. Evaluation of uncertainty in determination of Tar[J]. Modern Measurement and Test,2003,(6): 37-40. (in Chinese)
[19] 杨琴,彭忠,郑利锋. 卷烟主流烟气中CO测量不确定度的评定[J]. 现代测量与实验室管理,2004, (6): 37-38.Yang Qin, Peng Zhong, Zheng Lifeng. Evaluation of the measurement uncertainty of CO in mainstream cigarette smoke[J].Modern Measurement and Test, 2004,(6): 37-38. (in Chinese)
[20] 张威,王颖,唐纲岭,等. 连续流动法测定烤烟总植物碱的不确定度[J]. 烟草科技,2012,(8): 29-33.Zhang Wei,Wang Ying, Tang Gangling,et al. Uncertainty in determination of total Alkaloids in fl ue-cured tobacco with continuous flow method[J]. Tobacco Science & Technology,2012,(8): 29-33. (in Chinese)
[21] 许永,张霞,刘巍,等. 卷烟主流烟气中氢氰酸测定不确定度评价[J]. 云南大学学报:自然科学版,2011,33(5): 586-589.Xu Yong, Zhang Xia, Liu Wei, et al. Uncertainty evaluation of the determination of Hydrogen Cyanide in mainstream smoke[J].Journal of Yunnan University :Natural Sciences Edition, 2011,33(5): 586-589. (in Chinese)
[22] 张霞,许永,刘巍,等. 离子色谱法测定卷烟主流烟气中氨含量的不确定度评定[J]. 化学分析计量,2011, 20(4): 16-19.Zhang Xia, Xu Yong, Liu Wei, et al. Evaluation of uncertainty in the determination of Ammonia in cigarette mainstream smoke by ion chromatography[J]. Chemical Analysis and Meterage, 2011, 20(4): 16-19. (in Chinese)
[23] 黄光莉,林琳,陶里,等. 卷烟主流烟气中苯酚测定的不确定度[J]. 烟草科技,2013, (6): 64-68.Huang Guangli, Lin Lin, Tao Li, et al. Uncertainty in determination of Phenol in mainstream cigarette smoke[J].Tobacco Science & Technology, 2013,(6): 64-68. (in Chinese)
[24] 崔柱文,孔维松,刘巍等. HPLC法测定卷烟主流烟气中苯酚的不确定度评定[J]. 安徽农业科学,2012,40(14): 8212-8213.Cui Zhuwen, Kong Weisong, Liu Wei, et al. Assessment of uncertainties in the determination of Phenol in mainstream smoke of cigarette by HPLC[J].Journal of Anhui Agri.Sci.,2012,40(14): 8212-8213. (in Chinese)
[25] 王颖,刘贤杰,张亮,等. 高效液相色谱法测定卷烟主流烟气中巴豆醛含量的不确定度评定[J]. 广东化工,2013,40(16):207-208.Wang Ying, Liu Xianjie, Zhang Liang, et al. Evaluation of uncertainty in determination of Crotonaldehyde in cigarette mainstream smoke by high performance liquid chromatography[J]. Guangdong Chemical Industry,2013,40(16): 207-208. (in Chinese)
[26] 芮晓东,许永,张霞,等. 卷烟主流烟气中NNK测量不确定度评定[J]. 化学分析计量,2012,21(1): 7-10.Rui Xiaodong, Xu Yong, Zhang Xia, et al. Uncertainty evaluation of the determination of tobacco specific NNK in mainstream smoke[J]. Chemical Analysis and Meterage,2012,21(1): 7-10. (in Chinese)
[27] 王永梅,张玉璞,张昌壮,等. 气相-质谱联用法测定主流烟气总粒相物中苯并[a]芘测量不确定度评定[J]. 哈尔滨师范大学自然科学学报,2014,30(5): 82-86.Wang Yongmei, Zhang Yupu, Zhang Changzhuang, et al.Uncertainty assessment in determination of Benzoapyrene in particulate matter of mainstream smoke by GC-MS[J]. Natural Science Journal of Harbin Normal University, 2014,30(5): 82-86. (in Chinese)
[28] 陈韶.测量不确定度评定中建立数学模型的探讨[J].计量与测试技术,2010, 37(1): 48-49.Chen Shao. Discussion on how to establish the statistical model puring estimating measurement uncertainty[J]. Metrlogy and Measurement Technique, 2010, 37(1): 48-49. (in Chinese)
[29] JJF 1059.1 测量不确定度评定与表示[S].2012.JJF 1059.1 Evaluation and expression of uncertainty in measurement [S]. 2012.
[30] 张虹. 加标回收率的测定和结果判断[J]. 石油与天然气化工,2000,29(1):50-52.Zhang Hong. Determination and result judgement of recovery rate of add standard[J]. Chemical Engineering of Oil and Gas,2000,29(1):50-52. (in Chinese)
[31] 冯秀文,高俊琴. 用回收率检验分析方法的准确度[J].光谱学与光谱分析,1995,15(3):87-90.Feng Xiuwen, Gao Junqin. Examination of analytical accuracy using recovery[J]. Spectroscopy and Spectral Analysis,1995,15(3):87-90. (in Chinese)
[32] JJF 1059.2 用蒙特卡罗法评定测量不确定度 [S].2012.JJF 1059.2 Monte Carlo method for evaluation of measurement uncertainty [S].2012.
[33] CNAS-GL06 化学分析中不确定度的评估指南[S].2006.CNAS-GL06 Guidance on evaluating the uncertainty in chemical analysis[S].2006.
Uncertainty in determination of components in mainstream cigarette smoke
WANG Lv1, CHEN Xianfei1, WANG Jin1, YAO Wei1, ZHANG Yu1, ZHANG Wei2, FENG Qunzhi1,CAI Yuexiu1
1. Shanghai Tobacco Group Co., Ltd., Shanghai 200082, China 2. China National Tobacco Quality Supervision & Test Center, Zhengzhou 450001, China
In order to study uncertainty in determination of mainstream cigarette smoke components, data veri fi cation method and measurement uncertainty of di ff erent samples and di ff erent models of smoking machine were determined by measuring hydrogen cyanide, ammonia, phenol, crotonaldehyde, NNK and benzo [a] pyrene. GUM method was chosen and measurement model was established by simplifying calculation formula. Combined standard uncertainty and expanded uncertainty were calculated based on relevance of measurement data. Inter-laboratory experiments were carried out, and repeatability and reproducibility were used to verify validity of measurement data. Measurement uncertainty of di ff erent cigarette samples was estimated and regressed to determine function. Measurement uncertainty with di ff erent smoking machine models was veri fi ed by con fi dence interval of curve fi tting. Results showed that: 1) The GUM method was applicable to measurement uncertainty estimation of cigarette mainstream smoke components. The variation between and within groups were the largest weight components. The ratios of expanded uncertainty and corresponding measurement value were 6.2% ~ 14.4%, when the coverage factor (k) was 2. 2) The inter-laboratory repeatability and reproducibility experiments were e ff ective methods to validate data. 3) There exists correlation between measurement values and measurement uncertainty of di ff erent samples, and the estimated values of measurement uncertainty could be obtained with measurement values through functional relation. 4) There were di ff erences in measurement results and measurement uncertainty between di ff erent smoking machine models, but didn’t a ff ect measurement uncertainty estimation signi fi cantly.
cigarette; mainstream cigarette smoke; related components; measurement uncertainty
王律,陈贤飞,王瑾,等. 卷烟主流烟气中相关成分测量不确定度评定的研究[J]. 中国烟草学报,2016,22(1)
国家烟草专卖局标准制定项目“卷烟主流烟气中相关成分测量不确定度评定指南”(计划号:国烟科[2013]115号);上海烟草集团有限责任公司科技项目“卷烟主流烟气中相关成分测量不确定度评定指南”(K2013-1-043p)
王律(1973—),工程师,主要从事卷烟质量检验、烟草化学研究,Tel:021-61669632,Email:wangl@sh.tobacco.com.cn
冯群芝, Email:fengqz@sh.tobacco.com.cn
2015-01-28
:WANG Lv, CHEN Xianfei, WANG Jin, et al.Uncertainty in determination of components in mainstream cigarette smoke[J].Acta Tabacaria Sinica, 2016, 22(1)
