米波雷达低仰角测高的地形补偿方法

马献德，路彬彬，冯　兵

(南京电子技术研究所，　南京 210039)



·总体工程·

米波雷达低仰角测高的地形补偿方法

马献德，路彬彬，冯兵

(南京电子技术研究所，南京 210039)

由于多径效应，米波雷达低仰角测高一般通过空间平滑去相干，或者由反射模型建立合成导向矢量，进而采用多信号分类、最大似然等仰角匹配算法来实现。但固定系数反射模型通常只能适用于平坦地形，在起伏地形条件下建立准确的变系数反射模型极困难。文中分析了目标位置变化过程中地面反射系数的变化情况，提出了一种通过检飞数据直接估算合成导向矢量的方法，以提高起伏地形条件下米波雷达低仰角测高算法的稳健性和精度。实验结果表明了所提方法的有效性，特别在目标距离较远时，使用所提方法得到的仰角精度明显优于传统方法。

起伏地形；测高；米波雷达；合成导向矢量；检飞；地形补偿

0　引　言

地形起伏对米波雷达测高的影响源于多径干涉。在平坦地形下，反射波与直达波之间存在比较严格而固定的幅度相位关系，可以先空间平滑去相干，再应用多信号分类(MUSIC)或最大似然(ML)等仰角匹配算法，本文称之为“空间平滑-仰角匹配” 算法；或者应用几何方法进行反射建模，通过直达波与反射波合成导向矢量，再应用仰角匹配算法实现高分辨仰角估计，本文称之为“反射建模-仰角匹配”算法。

在起伏地形下，反射波与直达波仍然相干，但两者之间的幅相关系与平坦地面不同，且会随着反射面的起伏发生难以计算的变化；两者之间的幅相关系对于不同的阵地也互不相同。而上述“空间平滑-仰角匹配”算法或“反射建模-仰角匹配”算法均建立在反射波与直达波在平坦地形的直达波-反射波幅相关系的基础上，在起伏地形下仰角误差显著增加。

目前为止，对米波雷达低仰角测高方法的研究仍主要针对平坦地形，对于起伏地形下测高算法的研究还比较少见。文献[1]针对基于波瓣分裂的米波雷达“比相比幅”测高方法，分析了地面反射系数的影响因素及其对高度测量精度的影响，探讨漫反射对测高方法的影响，对基于仰角匹配测高方法的地形影响分析有一定的借鉴意义。文献[2]把地形的影响归结为反射面相对于雷达的高度差的变化，提出一种“仰角-高度差”二维搜索，并进一步提出“基于二次雷达信息对地形参数优化的一维搜索模型”，以减小计算量的地形起伏解决方案，通过仿真验证了其相对于传统算法的优越性，虽然反射点高度一个信息难以完全描述反射状态，与实际情况差别较大，但基于二次雷达信息的模型很有启发意义。

针对起伏地形对米波雷达低仰角测高的影响，本文通过分析目标距离发生变化时，其反射波反射区域的大小以及反射区域移动的情况，指出在一般起伏地形条件下，即使目标位置发生大范围变化，其反射区域的变化并不大，据此提出了一种通过事先策划的检飞录取数据，直接补偿“直达波-反射波合成导向矢量”，实现地形补偿的方法。

1　地形起伏对反射建模的影响

本文以下均假定已通过对距离、方位波门进行处理，使得所接收的雷达回波数据中在一个距离单元只有一个目标(在实践中这是完全可以做到的)，由于多径效应，该目标的回波数据包含了直达波和反射波。在平坦地形下，一般可认为固定的空间只有一条反射路径[3]，接收数据模型可按如下形式建立

X(t)=AS(t)+N(t)=

(1)

式中：X(t)为接收数据；A为导向矢量矩阵；S(t)为信号矩阵；N(t)为噪声矩阵；a(θ1)与a(θ2)分别为直达波与反射波的导向矢量，θ1与θ2分别为直达波与反射波的入射角；s(t) 与ρs(t-τ)分别为直达波与反射波的时域信号，ρ为反射系数，τ为反射波信号相对于直达波信号的延时。以下分析在起伏地形条件下，接收数据模型中各参量如何受到地形起伏的影响。

1.1地形起伏对反射波-直达波幅相关系的影响

平坦地形与起伏地形的反射模型示意图，如图 1所示。一般雷达架高和垂直孔径远小于目标高度，在目标距离很远的情况下，无论是平坦地形还是起伏地形，只要没有视线上的遮挡，各垂直单元处的直达波目标仰角相等，信号复包络相同，相位线性变化。

图1　起伏地形与平坦地形反射情况比较

在平坦地形下，如图1a)所示，各垂直单元对应的反射波目标位置可以认为是在同一个位置，因此，也可认为各垂直单元处反射波信号的复包络相同，相位线性变化。

在起伏地形下，如图1b)所示，由于反射点处的地表几何状态发生变化，各垂直单元对应的反射波目标位置不能认为是在同一个位置，因此，各垂直单元的θ2之间会有不可忽视的差别，τ也是如此。故θ2和τ应分别视为垂直单元序号的函数θ2(i)和τ(i)。另外，目标运动会导致反射点的移动，而且其位置难以预测，θ2和τ应进一步视为直达波仰角、垂直单元序号与时间的函数θ2(θ1,i,t)和τ(θ1,i,t)。

因此，接收数据模型应当改写为

X(t)=s(t)a(θ1)+ρb(θ2,t)+N(t)

(2)

其中，

(3)

即在起伏地形条件下，各垂直单元处的反射波信号不再满足“复包络相同，相位线性变化”。要建立精确的接收数据模型，必须分别得到每个时刻、不同直达波仰角、各个垂直单元处θ2和τ的精确值。

分析结论：地形起伏对反射波-直达波幅相关系有很大影响。

1.2地形起伏对接收噪声的影响

接收机系统内部噪声显然与地形起伏无关，只需考虑外部噪声，即天线噪声温度与地形起伏的关系。

天线噪声温度Ta，即

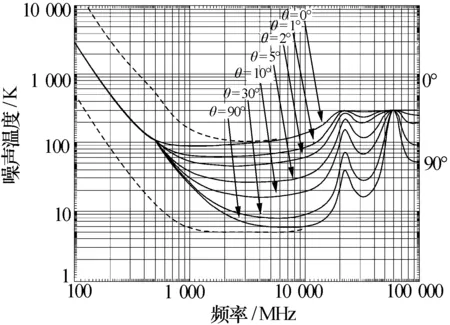
图2　架设在地面的理想天线(无损耗，无指向地面的副瓣)的噪声温度与频率的关系

另外，对不同的垂直单元和不同的时刻，一般可认为接收噪声N(t)是独立同分布的，因此，接收噪声与时刻、垂直单元也不相关。

分析结论：地形起伏对接收噪声无明显影响。

1.3地形起伏对反射建模影响的综合结论

综上所述，地形起伏对反射波-直达波幅相关系有很大影响，而对接收噪声无明显影响。

对地形进行补偿的方法应当着眼于反射波-直达波幅相关系参数，即反射波相对于直达波的幅度比和相位差，以下简称为“反射状态参数”。

2　检飞补偿法的主要思想

根据上述分析，地形起伏对反射建模的影响主要是对反射状态参数的影响。因此容易产生以下两种处理思路：

1) 地形测量法。对雷达前方观测范围内、地表反射范围内的地形参数进行测量(主要是测量点处的坐标)，利用测量结果修正反射模型。如果测量结果足够精确，则理论上可完全消除地形起伏的影响；但此方法地形测量工作量大、成本高、不易达到高的测量精度，反射建模和匹配的运算量巨大，且对不同阵地缺乏通用性。因而此方法工程上并不实用。

2) 地形搜索法。在MUSIC等方法对仰角的搜索过程中，增加对反射状态参数的搜索。从理论上说，这种方法不需任何近似假设和先验知识，能取得较高精度；但由于对每个垂直单元均需单独搜索反射状态参数，此方法计算量极其巨大，工程上不可实现，因而无法采用。文献[3]简化为只搜索反射点高度，虽然计算量得以降低，但根据本文前述分析，反射点高度难以完全描述反射状态，与实际情况差别较大。

而本文提出一种“检飞补偿法”，其主要思想是：尽管地形存在起伏，难以直接建立准确的反射模型，但如果可以找到地形起伏情况下，仰角估计算法中不变或者变化较小的某些关键参量，通过一次或少数几次检飞估算出这些参量，则可以利用这些参量重建有效的反射模型，实现仰角估计。

首先，地形起伏本身并不随时间而变，只是当目标运动时，其回波在反射面上的反射状态参数可能发生变化；其次，如果能够根据搜索的直达波仰角，直接估算合成导向矢量，则不需要知道各个θ2和τ的精确值即可得到较精确的接收数据模型。为了实现有效的补偿，对同一个垂直单元，要求估算合成导向矢量时的反射状态时(即检飞时)与补偿时的反射状态基本相同。因为，补偿时就是雷达实际运行的状态，目标斜距、仰角等参数都可能发生很大的变化。所以，补偿有效的前提就等价于确保当目标运动中某个参数不变，而其他参数变化很大时，反射状态参数基本不变。

以下通过理论分析和计算，证明对同一个空间(方位、距离、高度)单元，当目标仰角不变时，在目标斜距变化的一个很大范围内，反射状态基本不变。因此，可以通过覆盖所需仰角范围的一次或多次检飞，建立“目标仰角-反射状态参数”的关系(或等价为“目标仰角-合成导向矢量”的关系)并存储起来，在雷达正常工作中，利用该关系对反射建模过程进行地形补偿，实现稳健的测高算法。

2.1反射区域及其变化

尽管通常考察平坦地面反射时可以把反射处看作一个点，但由于每个天线单元都有一定的孔径，而反射面一般情况下可视为连续可微曲面。所以反射处实际上是一个反射区域[5](起伏地形情况下可能有多个反射区域)，到达雷达接收天线的反射回波是整个(或多个)反射区域内各点的反射波的总和。在平坦地形情况下，把反射处视为一个反射点是正确合理的，但在起伏地形情况下，则应当考虑反射区域，如图3a)所示。当目标位置发生变化时，天线单元对应的起伏地形反射区域也会变化，如图3b)所示。

图3　反射区域及其变化示意图

目标位置变化前后，从空中俯视的反射区域变化情况，如图4所示。反射区域半径为R，由初始时的区域1移动到区域2，位移量为D。显然，如果D比R小得多，则区域1和区域2大部分都是重叠的，只要地形起伏不很严重，则无论地形起伏的具体情况如何，目标位置变化前后的反射状态都接近于相同；反之，如果D比R大得多，甚至D>2R，则两个区域的重叠区域很小，甚至没有重叠，则目标位置变化前后的反射状态会有一定的差别(取决于地形起伏情况)。

图4　反射区域尺度和位移示意图(俯视)

因此，在地形起伏不很严重的情况下，如果目标仰角一定时，目标运动导致的反射区域水平位移相对于反射区域本身的尺度来说比较小，则可认为反射区域近似不变，从而整个反射状态也近似不变。

这样，对于一个固定的反射阵地，就有可能通过检飞，得到关于目标仰角与反射状态之间关系的先验信息，从而可用于实际测高的地形补偿。

2.2反射区尺度的分析

反射区的尺度受到多种因素影响，本文只须考虑垂直天线单元孔径这个最重要的因素，据此可计算反射区的半径。计算条件：电波频率为145 MHz，垂直单元总数为16，单元间距为1m，最下方单元架高为4.73 m，单元孔径为0.8 m。计算结果如图 5所示。

图5　反射区半径(图例表示目标仰角)

由图 5可得到如下三点结论：

1)目标斜距固定时，对同一个垂直单元，仰角越大，反射区半径越小。

2)目标仰角固定时，对同一个垂直单元，在目标斜距为100 km～300 km，反射区半径几乎不随目标斜距而变化。

3)目标斜距、仰角都固定时，反射区半径几乎与单元架高无关。

综上所述，当垂直天线单元数目、孔径、间距、架高等基本参数确定后，反射区半径主要随目标仰角而变化，几乎不随目标斜距和单元架高而变化。

2.3反射区位移的分析

计算条件同上，目标方位和仰角固定，而目标斜距在100 km～300 km变化时，各垂直单元反射区的水平最大位移量，如图6所示。

图6　各垂直单元反射区域的水平最大位移量(图例表示目标仰角)

由图6可得到以下三点结论：

1)目标斜距固定时，对同一个垂直单元来说，仰角越大，反射区位移越小。

2)目标仰角在1°及1°以上，目标斜距为100 km～300 km的区间内仰角不变时，反射区的位移基本上小于反射区半径的一半。即相对于反射区的大小来说，虽然目标斜距变化了200 km，但反射区的水平位移很小，反射区的大部分仍与原反射区重合，这表明反射状态的变化很小。

3)目标斜距、仰角都固定时，反射区位移随单元序号(架高)增加而增大，增大速度也随单元序号(架高)增加而增大，且仰角越大，增大得越慢。

以上关于反射区大小及反射区位移的分析结论虽然是在地形平坦的条件下得到的，但对于地形起伏不很严重的情况，其结果基本上也是适用的。

2.4检飞补偿法的具体步骤

综上所述，当地形起伏不很严重时，因为反射状态与目标仰角之间存在密切关系，而与目标斜距几乎无关，所以可通过以下三种方法进行地形补偿：

1) 设计一次或多次检飞，要求控制飞行高度和距离，以覆盖目标所有可能的仰角范围。

2) 设计检飞程序，建立垂直单元、仰角与合成导向矢量的对应关系，并存储为数据表格。这一步实际上就是建立了起伏地形下的反射模型。

3) 设计补偿程序，在方法2)所存储的“仰角-合成导向矢量”表格的基础上利用MUSIC或最大似然等算法进行仰角估计，即可补偿地形起伏的影响，实现较高精度的仰角估计。

3　检飞补偿法的具体步骤和实验验证

限于条件，本文采用以往实验中记录的回波数据库进行算法验证。数据库中包含多次检飞的数据，采用其中一些批次的数据补偿其他批次的数据，并与直接用“反射建模-仰角匹配”算法的结果进行比较，以验证上述地形补偿方法的有效性。

实验参数：电波频率为145 MHz，垂直单元总数为16，单元间距为1 m，最下方单元架高4.73 m。检飞时目标全部在同一方位上等高径向飞行，因此，较近处的合成信噪比(多脉冲相参积累及各单元数据进行波束形成后的信噪比)较高；较远处的合成信噪比较低。阵列前方反射区的地形有一定起伏，但未进行实际的地形勘测。

图7是对某次检飞数据A的仰角估计结果，其中分别给出了不补偿、用另外一次检飞数据B进行补偿、用另外3次检飞数据B、C、D取平均值进行补偿的计算结果，同时也给出了数据A的合成信噪比。数据B、C、D在仰角上覆盖了数据A的仰角范围。根据式(2)，多次检飞取平均类似于积累过程，等效于提高了信噪比。为便于比较算法效果，图中剔除了个别误差绝对值大于2°的孤立野值点(在实践中这是完全可以做到的)。

图7　检飞补偿法实验结果

由图 7可以看到，相对于不补偿的“反射建模-仰角匹配”算法，在目标斜距较远处，检飞补偿法具有明显的优势；在近距离处，两者差别不大；采用多组数据补偿另一组数据的效果优于采用一组数据补偿另一组数据的效果。

图8是采用同样方法补偿多组数据，分别剔除了个别误差绝对值大于2°的野值点后，按距离段计算仰角误差均方根值的统计结果。统计时，每隔1 km取一个距离点，计算以该距离点为中心的20 km距离段内仰角误差的均方根值。图例中，“不补偿”表示直接用“反射建模MUSIC”算法计算数据集{M}的结果，“补偿1”表示采用同一组数据B补偿数据集{M}的结果，“补偿2”表示采用数据B、C、D补偿数据集{M}的结果(其中数据B、C、D均不在数据集{M}中)。

图8　检飞补偿法实验统计结果

由图8可以明显看到，在240 km以上(此距离段合成信噪比只有约20 dB)，直接用“反射建模MUSIC”算法的仰角估计误差随着目标距离增加(从而信噪比也下降)而急剧增大，而采用检飞补偿法，在同样的距离段上，仰角估计误差的变化比较平缓。采用多组数据的补偿效果优于单组数据的补偿效果，这在近距离处两者差别不大，但在距离接近300 km时可看到，由于单组数据信噪比低，仰角估计误差有明显的增加，而多组数据的平均处理等效于提高了信噪比，从而有助于减小补偿后的仰角估计误差。

4　结束语

针对起伏地形对米波雷达低仰角测高的影响，本文通过分析目标位置发生变化时，其反射波反射区域尺度及反射区域位移的情况，指出在一般起伏地形条件下，即使目标位置发生大范围变化时，其反射区域的变化也很小。据此，本文提出了一种通过事先策划的检飞录取数据，直接补偿“直达波-反射波合成导向矢量”，不必对反射建模，即可实现地形适应的方法。实验结果验证了在地形起伏条件下，本文所提方法优于直接采用“反射建模-仰角匹配”的算法，在目标距离较远时，本文所提方法的优势明显；若采用多次回波数据补偿另一次回波数据，可得到更高的仰角估计精度。

本文所提的“检飞补偿法”的主要优点如下：

1) 能适应起伏地形，所得仰角估计精度优于直接采用“反射建模-仰角匹配”的算法。

2) 具备通用性，能适应不同阵地的地形，改变阵地时不需更改系统的任何软硬件设置。

3) 无须进行任何地形测绘，只须借助若干次检飞录取的数据，操作简单方便。

4) 在算法上不需要进行多维参数搜索，计算量小，由于检飞数据是事先录取的，实际使用中其计算量比“反射建模-仰角匹配”算法还小。

“检飞补偿法”工作展望：

1) 进一步减小检飞工作量。因为不同方位上的地形情况可能有差异，所以目前本文所提方法中，检飞时须在不同的方位上分别进行，录取相应的数据并存储，补偿时根据目标方位角读取对应的检飞数据。应改进“检飞补偿法”，以进一步减小检飞的工作量。

2) 严重起伏地形的补偿。前述对反射区大小和位移的分析只能适用于地形起伏不很严重的情况，如果地形起伏非常严重，则分析结论不能套用。应改进“检飞补偿法”，使其可用于严重起伏地形。

[1]陈伯孝, 胡铁军, 郑自良, 等. 基于波瓣分裂的米波雷达低仰角测高方法及其应用[J]. 电子学报, 2007, 35(6): 1021-1025.

CHEN Baixiao, HU Tiejun, ZHENG Ziliang, et al. Method of altitude measurement based on beam split in VHF radar and its application[J]. Acta Electronica Sinica, 2007, 35(6): 1021-1025.

[2]杨雪亚. 米波雷达阵列超分辨和测高方法研究[D]. 西安: 西安电子科技大学, 2011.

YANG Xueya. Study on array super-resolution and altitude measurement in VHF radar[D]. Xi′an: Xidian University, 2011.

[3]BLAKE L V. Radar range-performance analysis[M]. Lexington, Mass: Artech House, 1988.

[4]SKOLNIK M I. 雷达手册[M]. 2版. 王军, 林强, 米慈中, 等译. 北京: 电子工业出版社, 2003.

SKOLNIK M I. Radar handbook[M]. 2nd ed. WANG Jun, LIN Qiang, MI Cizhong, et al translate. Beijing: House of Electronic Industry, 2003.

[5]胡晓琴, 陈建文, 王永良. 米波雷达测高多径模型研究[J]. 电波科学学报, 2008, 23(4): 651-657.

HU Xiaoqin, CHEN Jianwen, WANG Yongliang. Research on meter-wave radar height-finding multipath model[J]. Chinese Journal of Radio Science, 2008, 23(4): 651-657.

马献德男，1983年生，博士，高级工程师。研究方向为雷达总体技术。

Terrain Compensation Approach for Height-finding Method of VHF Radar

MA Xiande，LU Binbin，FENG Bing

(Nanjing Research Institute of Electronics Technology,Nanjing 210039, China)

Due to multipath effect, height-finding methods of VHF radar aiming at low-altitude targets are generally constructed by coherence-reducing space-smoothing techniques or synthetic steer vector techniques, both via reflection models, followed by elevation-matching algorithms such as MUSIC or maximum-likelihood. However, traditional reflection models usually can only be applicable for flat reflecting surfaces. It is extremely difficult to build variant-coefficient reflection models for fluctuant terrains. In this paper, the varieties of reflecting-coefficient during target movements are analyzed, and an approach is proposed using flight test data to directly estimate the synthetic steer vectors, in order to guarantee the robustness and precision of low-altitude height-finding algorithms confronting the fluctuant terrains. The experimental results validate the proposed method, showing that the precision gained by the proposed method can be much better than traditional algorithms when the target is very far and signal-noise ratio is quite low.

fluctuant terrain; height-finding; very high frequency (VHF) radar; synthetic steer vector; flight test; terrain compensation

10.16592/ j.cnki.1004-7859.2016.09.002

马献德Email：mxdmxd@foxmail.com

2016-04-24

2016-06-28

TN953

A

1004-7859(2016)09-0007-05