可实现误差估计的移相量计算方法
2016-11-15袁道成何建国
刘 乾,袁道成,何建国
(1.中国工程物理研究院 机械制造工艺研究所,四川 绵阳 621999;2.西安交通大学 机械工程学院,陕西 西安 710049)
可实现误差估计的移相量计算方法
刘乾1*,袁道成1,2,何建国1
(1.中国工程物理研究院 机械制造工艺研究所,四川 绵阳 621999;2.西安交通大学 机械工程学院,陕西 西安 710049)
针对移相干涉仪中移相器的标定,提出了一种基于干涉图计算移相量的迭代方法。该方法分为两步:首先假设移相量已知,构建三元最小二乘方程计算位相;然后假设位相已知,构建二元最小二乘方程计算移相量,同时依据三角函数关系和遍历原则,建立估算移相量计算误差的参数。利用计算机仿真和实验验证了提出方法的有效性。计算机仿真显示:提出的方法比已有算法计算精度更高,而且误差估计值与实际计算误差偏离小于15%。在Fizeau干涉仪上开展了验证实验,利用两个电容位移传感器测量了镜架的位移。计算结果与电容传感器测量结果非常吻合,最大偏差仅为0.7 nm。另外,利用本文方法得到的误差估计值为0.52 nm,显示测量结果和计算结果的偏差在误差估计值范围内。所提出的方法可以高精度地提取移相量,且能给出移相量计算误差,是一种简单可靠的移相器标定方法。
移相干涉仪;移相器;标定;误差估计;迭代算法
1 引 言
移相干涉仪因其分辨率高和重复性好而成为波面测量的一种重要仪器[1]。移相过程可以使干涉仪采集多帧干涉图计算每一像素点的位相,从而获得高的空间分辨率。测量中移相量应等于预设值,否则将导致波面测量误差,如经典的四步移相中,10 nm的移相误差将导致20 nm波长的波面误差[2]。然而,无论压电陶瓷[3]还是波长调谐[4]方式的移相,均存在一定的非线性。因此,需要对移相干涉仪的移相器进行高精度校正[5]。另外,移相器的老化也将破坏移相精度,需要再次重新标定。研究者们采用了多种光学方法对压电陶瓷的位移和电压之间的关系进行标定[6-7]。
由于移相干涉仪带有可作为长度计量基准的激光器,因此研究者提出了一些从干涉图提取移相信息的方法,无需另用其他仪器。这些方法大致可以分为三类。第一类方法基于干涉图的灰度统计信息[8-9],这类方法假设了一定的条件,如干涉图背景和调制度在空间上无变化或波面位相在[0,2π]是均匀分布的。第二类方法基于多参数的优化[10-11],以多个移相量作为自变量建立目标函数,通过优化求解移相量。第三类方法基于迭代优化[12-13],在该类方法中将空间相关参数和移相相关参数分别作为已知量去求解对方,经多次迭代求解移相量。赵智亮等曾以迭代算法为基础通过干涉图计算移相量,在干涉仪未增加硬件的情况下构建了移相误差的自校正系统[14]。这些方法都能很好地从干涉图中提取移相量,但对于实际使用中噪声或其他非理想因素造成的计算误差,上述算法均不能给出误差情况。因此,利用这些算法标定移相器时难以估计计算结果的可靠程度,这在一定程度上降低了标定的可信性。本文对先进迭代算法[12]进行改进,提出了一种带有精度指示的算法,利用干涉图迭代计算中的冗余信息,来估算移相量的计算误差,可以同时给出移相量的计算结果和最大误差。在给出了算法原理的基础上,通过计算机仿真和实验对算法性能进行了验证。
2 算法原理
移相干涉测量采集到的干涉图光强可以表示为:

(1)
其中,下脚标i(i=1,2,…,M)和j(j=1,2,…,N)分别表示帧序号和像素序号,Aj、Bj、φj分别为第j个像素的背景、调制幅度和波面位相,δi为第i帧干涉图相对于第一帧干涉图的移相量。上标t表示理论光强值。在式(1)中仅光强为已知量,等号右边的4个参数均是未知量,因此迭代算法是求解该问题的一个有效途径。展开式(1)中的余弦项,式(1)可转换为与帧参数和像素参数的线性关系式:
Aj+bjbi′+cjci′,
(2)



(3)
其中
αj=[Aj,bj,cj]T,


式(3)中的求和号是对所有干涉图序号求和。可以计算波面位相为:
φj=arctan(-cjlbj).
(4)


(5)
其中

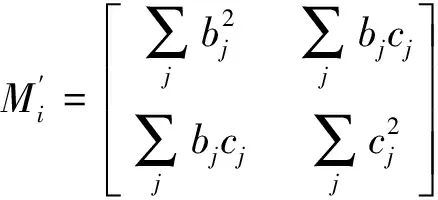


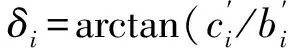
(6)
在第二步中充分利用第一步的计算结果,将背景和调制幅度视为空间参数,而与干涉图帧序号无关。这样,将先进迭代算法中的三阶最小二乘方程降为二阶,减少了运算量。

Δi=picosδi-qisinδi.
(7)
式(7)可写为

(8)
其中

(9)


(10)
比较式(8)和式(10)可以看出,移相量的计算误差Δi与参量vi分别是以pi2+qi2平方根为幅值、δi+εi的余弦和正弦值。若不存在计算误差,即pi=qi=0时,vi=0。由于干涉图噪声分布对每个像素是遍历的,因此,每帧干涉图得到的pi2+qi2近似相等。而每个像素的噪声是随机分布的,即对于每帧干涉图,εi随机分布在[0,2π]区间内。因此,对于i=1,2,…,M,Δi的最大值E与vi的最大值近似相等。这表明,在迭代过程中可利用vi的最大值V来作为移相量计算误差的指示参数。
本文算法与先进迭代算法[12]的最大区别在于将干涉图背景和调制幅度视为空间变量的函数,而与帧序号无关。此改进更符合移相干涉测量的实际情况,并可以减小一定的计算量,更重要的是可以通过式(5)方程解的内在联系建立一个估算误差的参数V。该参数的建立使得计算出移相量的同时还可以得到计算结果的误差范围、了解计算结果的可靠程度。
3 计算机仿真


图1 移相量计算误差E和误差指示参数V的变化曲线Fig.1 Phase shifts estimation errors E and accuracy indicator V as a function of iteration cycles

图2 25次迭代后干涉图的移相量计算误差和误差估算值viFig.2 Error of phase shift estimation and vi of each interferogram after 25 iteration cycles

图3 εi的统计分布示意图Fig.3 Schematic of statistic distribution of εi
另外,仿真研究了干涉图噪声对误差估算的影响。除叠加的噪声外,其他条件与上文相同,仿真了移相量计算误差E和误差指示参数V在不同方差噪声下的关系,如图4所示(彩图见期刊电子版)。可以看出,E随噪声的增大而增加,V相对于E的误差小于15%,表明在不同状况下误差指示参数V具有较高的可信度。

图4 移相量计算误差E和误差指示参数V与噪声的关系Fig.4 Phase shifts estimation errors E and accuracy indicator V as a function of noise variance
收敛性也是迭代算法需要考虑的重要问题。为考察算法的收敛性,另外生成12帧π/2移相的干涉图,移相量初始迭代值选为π/5,此时,结果迭代未收敛到正确值。这是因为空间参数A、B和φ基本上被初始值限制,因此收敛到初始值附近的局部最小值。而先进迭代算法中将背景和调制度强制设置为各个像素点相同,以此避免收敛到局部最小值。考虑到本文算法和先进迭代算法各自的优势和不足,因此在计算时先使用先进迭代算法寻找全局最小值,然后使用本文算法进行迭代,可以得到更精确的结果,并得到误差指示参数V。对上述的12帧干涉图采用这种联合方法,以π/5为初始值,首先用先进迭代算法计算15次,然后采用本文算法迭代15次,得到最大计算误差E和误差指示参数V随迭代次数的变化曲线,如图5所示。可见,先进迭代算法可快速收敛到全局最小值,但第11次迭代后最大误差不再减小,这是先进迭代算法将所有像素的背景和调制量强制设置为相同值所致。以先进迭代算法的计算结果作为初始值,本文算法可以进一步减小计算误差,收敛到更精确的结果。

图5 先进迭代算法和本文算法联合迭代的误差曲线Fig.5 Phase shift estimation error as a function of iteration cycles with combination method
4 实 验
在干涉仪平台上进一步验证算法性能。实验装置示意图如图6所示。干涉仪为Fizeau型平面干涉仪,激光器波长为632.8 nm,频率稳定性优于1 MHz/min,功率为闭环控制。CCD分辨率为512×512,灰度级为8 bit。通过压电陶瓷驱动器(PZT)推动被测镜产生移相。PZT通过内置的应变片形成闭环反馈,标称定位精度可达1 nm。以平晶表面作为测试对象,其面形的PV值约0.15λ。采用两个重复性精度为0.15 nm的电容位移传感器(CDS,Micro-Epsilon 6500-CS005)测量金属镜架的移动。为减小电容传感器的非线性,事先对电容传感器进行校准。实验装置整体放在气浮隔振平台上,采用遮挡方式抑制干涉腔的气流流动。全部测试在1分钟内完成,温度变化可忽略。预设移相量为π/4,即PZT预设每步移动39.6 nm,实验共采集12帧干涉图。为进一步消除激光器功率波动引起的干涉图参数变化,利用干涉图中非干涉区域像素灰度值为参考对干涉图进行校正[15]。

图6 实验装置示意图Fig.6 Sketch of experiment setup

图7 移相量的计算结果和测量结果对比图Fig.7 Calculation and measurement results of phase shifts
迭代时将移相初始值设为π/3。使用2.9 GHz CPU的计算机,80 s完成15次迭代,得到移相量的计算结果。将计算的移相量减去预设值π/4,得到移相量的偏差值,如图7所示。图7中同时给出了两个电容位移传感器的测量结果。可以看出计算结果与测量结果十分接近,最大相差仅约为0.7 nm(第11帧)。迭代计算得到的V为1.03×10-2rad,对应632.8 nm的波长约为0.52 nm。图8给出了各帧干涉图的误差参数vi,其中v1的绝对值最大,即取V=0.52 nm。以±0.52 nm作为误差限,在图7上标出计算结果的误差区间,可见使用电容位移传感器测量的位移基本被纳入到误差区间内,仅在第11帧偏差稍大。实验结果表明,计算的移相量与传感器测量结果相符,且算法给出的误差区间能够较正确地给出计算结果的大致误差。虽然实验在对机械式移相干涉仪上进行,但本文算法也可应用于波长调谐移相。

图8 15次迭代后每帧干涉图的误差估算值viFig.8 Phase shifts estimation error vi after 15 iteration cycles
5 结 论
为了简便、可靠地标定移相干涉仪的移相器,本文提出从干涉图计算移相量的迭代算法。该算法对干涉图进行了合理的假设,计算精度得以提高。该算法还可以提供移相量计算误差的估算值,可以为计算结果的可靠性提供一定的参考依据。通过计算机仿真和实验证实了方法的有效性。实验中,传感器测试结果与计算结果有着很好的一致性,二者的偏差基本在误差参数范围以内。本文算法可以在不借助其他仪器的情况下实现对移相器的快速、可靠的标定。
[1]张宇, 金春水, 马冬梅, 等. 双光纤相移点衍射干涉仪装调技术 [J]. 红外与激光工程, 2014, 43(1): 145-150.
ZHANG Y, JIN CH SH, MA D M,etal.. Alignment technology for double-fiber phase-shifting point diffraction interferometer [J].InfraredandLaserEng., 2014, 43(1): 145-150. (in Chinese)
[2]VANWINGERDEN J, FRANKENA H, SMORENBURG C. Linear approximation for measurement errors in phase shifting interferometry [J].Appl.Opt., 1991, 30(19): 2718-2729.
[3]许素安, 谢敏, 孙坚, 等. 基于压电陶瓷光电相移驱动的大行程纳米定位系统[J].光学 精密工程,2014, 22(10): 2773-2778.
XU S A, XIE M, SUN J,etal.. Long range nano-positioning system based on optoelectronic phase-shift for piezoelectric actuator [J].Opt.PrecisionEng., 2014, 22(10): 2773-2778. (in Chinese)
[4]刘江, 苗二龙, 曲艺, 等. 基于光强自标定移相算法检测光学面形[J]. 光学 精密工程, 2014, 22(8): 2007-2013.
LIU J, MIAO E L, QU Y,etal.. Measurement of optical surface based on intensity self-calibration phase-shift algorithm [J].Opt.PrecisionEng., 2014, 22(8): 2007-2013. (in Chinese)
[5]OREB B F, FARRANT D I, WALSH C J,etal.. Calibration of a 300-mm-aperture phase-shifting Fizeau interferometer [J].Appl.Opt., 2000, 39(28):5161-5171.
[6]余有龙, 谭玲, 邹李刚, 等. 用光纤光栅传感器研究压电陶瓷的特性[J]. 光子学报, 2011, 40(7): 994-997.
YU Y L, TAN L, ZOU L G,etal.. Piezoelectric ceramic characteristics using fiber grating sensor [J].ActaPhotonicaSinica, 2011, 40(7): 994-997. (in Chinese)
[7]邓勇, 刘宁, 曹红蓓, 等. 基于Nd:YAG激光回馈干涉效应的PZT精密测量技术与系统 [J]. 红外与激光工程, 2014, 43(10): 3434-3438.
DENG Y, LIU N, CAO H B,etal.. Nd:YAG laser feedback interference effects based PZT precision measurement technology and system [J].InfraredandLaserEng., 2014, 43(10): 3434-3438. (in Chinese)
[8]XU J, LI Y, WANG H,etal.. Phase-shift extraction for phase-shifting interferometry by histogram of phase difference [J].Opt.Express, 2010, 18(23): 24368-24378.
[9]GUO H, ZHANG Z. Phase shift estimation from variances of fringe pattern differences [J].Appl.Opt., 2013, 52(26): 6572-6578.
[10]GUO H, YU Y, CHEN M. Blind phase shift estimation in phase-shifting interferometry [J].J.Opt.Soc.Am.A, 2007, 24(1): 25-33.
[11]GAO P, YAO B, LINDLEIN N,etal.. Phase-shift extraction for generalized phase-shifting interferometry [J].Opt.Lett., 2009, 34(22): 3553-3555.
[12]WANG Z, HAN B. Advanced iterative algorithm for phase extraction of randomly phase-shifted interferograms [J].Opt.Lett., 2004, 29(14): 1671-1673.
[13]LIU Q, WANG Y, HE J G,etal.. Phase shift extraction and wavefront retrieval from interferograms with background and contrast fluctuations [J].J.Opt., 2015, 17: 025704.
[14]赵智亮, 夏伯才, 陈立华, 等. 相移干涉测量中相移误差的自修正[J]. 光学 精密工程, 2013, 21(5): 1116-1121.
ZHAO ZH L, XIA B C, CHEN L H,etal.. Self-correction of phase step error in phase shifting interferometric measurement [J].Opt.PrecisionEng., 2013, 21(5): 1116-1121. (in Chinese)
[15]郝群, 朱秋东, 胡摇, 等. 一种在干涉图外圈开辟环形光强检测区的光强修正方法,中国: CN 101482394 B[P]. 2010.
HAO Q, ZHU Q D, HU Y,etal.. A light intensity correction method to open annular light intensity monitoring area in the outer interference pattern, China: CN 101482394 B[P]. 2010.

刘乾(1983-),男,山东单县人,博士,工程师,2006年于北京理工大学获得学士学位,2009年、2015年于中国工程物理研究院研究生部分别获得硕士、博士学位,主要从事精密测量、光学设计方面的研究。E-mail: liuqianblue@126.com

袁道成(1966-),男,河南信阳人,硕士,研究员,硕士生导师,1994年于四川大学获得硕士学位,主要从事精密测量的研究。E-mail: ydccaep@263.net
(版权所有未经许可不得转载)
Phase shift extraction algorithm with error estimation in phase-shifting interferometry
LIU Qian*, YUAN Dao-cheng, HE Jian-guo
(1.Institute of Machinery Manufacturing Technology,ChinaAcademyofEngineeringPhysics,Mianyang621999,China;2.SchoolofMechanicalEngineering,Xi’anJiaotongUniversity,Xi’an710049,China)*Correspondingauthor,E-mail:liuqianblue@126.com
For calibration of the phase shifter in a phase-shifting interferometer, an iterative algorithm was proposed to extract phase shift from a set of interference patterns. In each iteration cycle, the wavefront phase and phase shifts were calculated in two individual steps.Firsly, the phase shifts were assumed knowns and the calibration wavefront phase was retrieved from tri-variate equations. Then, the wavefront phase was assumed knowns and the phase shifts were extracted from bi-variate equations. Meanwhile, an error estimator to indicate the maximum calculation error of phase shifts was established based on the basic trigonometry and ergodic principles. The proposed algorithm was verified with computer simulations and experiments. The simulation results indicate that the proposed algorithm achieves higher accuracy, lightens the calculation burden, and the deviation between the error estimator and actual error is less than 15%. Validation experiments were carried out on a Fizeau interferometer. Two capacitive displacement sensors were employed in experiment to measure the actual phase increment. The results show that the extracted phase shifts are identical that from the proposed algorithm well and the maximum deviation is 0.7 nm. Moreover, the error estimator is 0.52 nm, which covers the deviation between calculation and measurement. It concludes that the proposed algorithm achieves higher accuracy and is more advantageous on that the calculation error can be given simultaneously, showing a convenient and reliable way to calibrate the phase shift for phase-shifting interferometers.
phase-shifting interferometer; phase shifter; calibration;error estimation; iterative algorithm
2016-05-06;
2016-06-22.
中国工程物理研究院超精密加工技术重点实验室基金资助项目(No.ZZ15008);能力提升课题资助项(No.2015B0405)
1004-924X(2016)10-2565-07
TH744.3
Adoi:10.3788/OPE.20162410.2565
