影响Czerny-Turner结构像散校正的因素

董科研，李欣航,2*，安　岩

(1.长春理工大学 空间光电技术研究所，吉林 长春 130022；2.长春理工大学 光电工程学院，吉林 长春 130022)



影响Czerny-Turner结构像散校正的因素

董科研1，李欣航1,2*，安岩1

(1.长春理工大学 空间光电技术研究所，吉林 长春 130022；2.长春理工大学 光电工程学院，吉林 长春 130022)

针对宽波段Czerny-Turner结构像散校正存在的问题，分析了影响光学系统像散校正的主要因素。基于发散光束照射平面光栅的像差理论，应用Matlab软件模拟分析了光学系统产生像散的原因和相应抑制方法的不足。讨论了了准直镜离轴角与聚焦镜离轴角的角度差值α和光学系统像散S之间关系，理论模拟了α取不同值时，宽波段C-T结构的全波段像散校正情况。为了验证理论分析的正确性，设计了光谱段为900～1 700 nm的消像散型光学系统，利用光学设计软件Zemax对该波段的光学系统进行了光线追迹和设计优化，并对设计结果进行处理和分析。结果显示：随着角度差值的逐渐增大，短波波段像散校正能力越来越强，像散校正能力提高了1.6倍左右；长波波段像散束缚能力越来越弱，像散校正能力平均降低了1.27倍左右。得到的结果表明：角度差值的合理选取可以为宽波段Czerny-Turner结构的像散校正提供理论指导。

光学设计；Czerny-Turner结构；像散校正；边缘波段

1　引　言

Czerny-Turner(C-T)结构型光谱仪是采用平面光栅作为分光元件的光学仪器，能够获取物质的光谱信息，为物质检测识别工作提供依据。C-T结构具有结构简单、分辨能力高、色散均匀、有效避免二次和多次衍射等优点。在天文学、物理学、生物学和化学等基础科学领域，光谱仪是常用的分析仪器；在工业和农业领域，光谱仪已经成为不可缺少的检测设备；在药物研制、环境保护和食品安全等领域，光谱仪可以实现在线实时的定性检测[1-4]。

像散是C-T结构光谱仪的主要像差。目前，抑制像散的主要方法有超环面聚焦镜[5]、自由曲面镜[6]、倾斜柱镜[7]、自由曲面柱镜[8]、楔形柱镜[9]、柱面反射镜[10]、一阶消像散方法[11]等。然而随着光谱仪的设计波段加宽，这些光谱仪校正方法均存在一定的局限性，即边缘波段像散的校正能力不足。为解决宽波段设计的难题，本文分析了结构中影响像散的主要因素，主要体现在准直镜离轴角和聚焦镜离轴角对系统的影响，从而为宽波段消像散光谱仪设计提供了理论依据。

2　像散理论

C-T结构的像散产生原因是光线离轴入射球面反射镜(准直镜和聚焦镜)，导致子午光束和弧矢光束的会聚能力不同，使得子午焦点和弧矢焦点分开的距离，如图1所示，成像光束在像面上形成一系列弥散斑。像散的存在不仅影响探测器对光束能量的接收，而且抑制光谱仪空间分辨率的提高，因此，分析C-T结构光谱仪的像散是十分必要的。

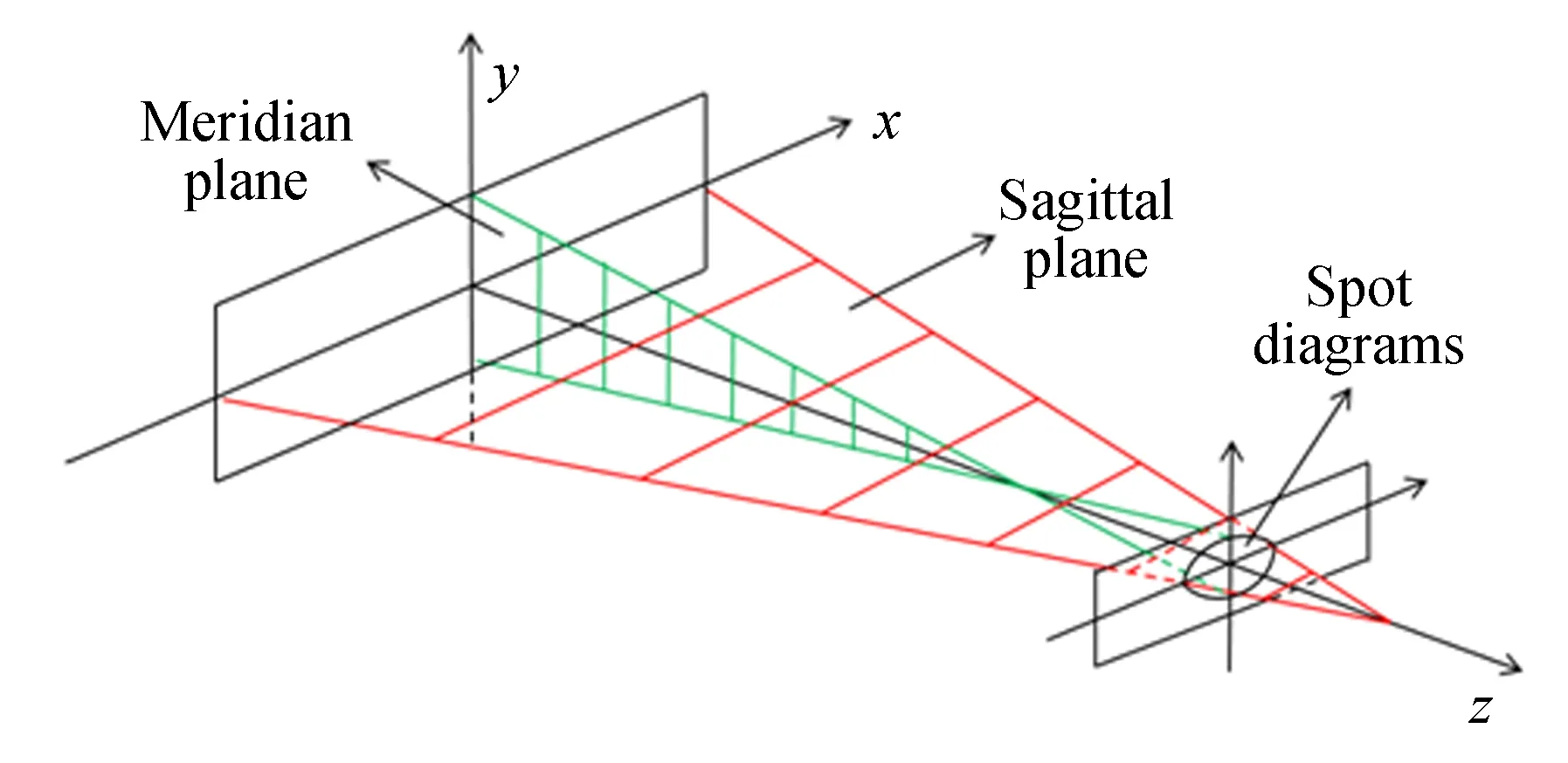
图1　像散产生原理图Fig.1　Production schematic of astigmatism

传统C-T结构由狭缝、准直镜M1、平面光栅、聚焦镜M2和探测器组成，如图2所示。其中α1为准直镜离轴角，α2为聚焦镜离轴角，i为平面光栅入射角，θ为平面光栅衍射角，σ为探测器倾角(探测器与垂直平面夹角)。光源发出的复色光通过狭缝进入光学系统，经准直镜第一次成像。由于准直镜离轴，导致弧矢像点和子午像点分开，根据细光束弧矢焦点和细光束子午焦点的位置公式，可以推导出准直镜的弧矢像距ls1和子午像距

图2　传统C-T结构原理图Fig.2　Schematic diagram of conventional C-T structure

lt1，即有：

(1)

其中:R1为准直镜的曲率半径，Lsc为狭缝与准直镜之间的距离。

经准直镜成像后的平行光束射向平面光栅，平面光栅在C-T结构中起分光作用，将入射的复色光分解为单色光谱。同理，可以推导出其弧矢像距ls2和子午像距lt2，即：

(2)

平面光栅分解后的单色光谱同时射向聚焦镜，经离轴聚焦镜成像，生成相应的弧矢像距ls3和子午像距lt3，即：

(3)

其中R2为聚焦镜的曲率半径。

经准直镜、平面光栅和聚焦镜成像后的光束，最终会聚在探测器上，形成一系列按波长排列的单色连续光谱。联立式(1)、式(2)和式(3)，得到光学系统的弧矢像距Ss和子午像距St为：

(4)

(5)

令聚焦镜离轴角与准直镜离轴角的角度差值为α，即α=α2-α1，将α2=α+α1带入式(4)和式(5)，可得：

(6)

(7)

由式(6)和式(7)可以看出，变量α和α1均影响弧矢像距Ss和子午像距St的大小。所以这里分别讨论了α和α1影响像散S=Ss-St的校正情况。

在同一光学系统下，当R1，R2，Lsc，i，θ，α1为定值时，仅存在变量α影响Ss和St。显然，cos(α+α1)越小，则Ss越小；α越大，sec(α+α1)越大，则St越大，故而Ss与St的差值减小，光学系统的像散校正能力增强；当R1，R2，Lsc，i，θ，α为定值时，仅存在变量α1影响Ss和St。同理，α1越大，cos(α+α1)越小，Ss越小，sec(α+α1)越大，St越大，故而Ss与St的差值减小，光学系统的像散校正能力增强。

可见，同一光学系统下，通过改变α和α1调整C-T结构的像散校正情况，可为后续的宽波段消像散型光谱仪设计提供理论依据。

3　像散校正分析

3.1平面光栅置于发散光路

平面光栅置于发散光路中，光束经过3次离轴反射式元件依次成像，生成相应的离散子午像距和弧矢像距。令Ss=St，可以推导出中心波长的零阶消像散条件[12]。

(8)

通过式(8)可以有效消除C-T结构中心波长处的像散。随后，D.R.Austin等[11]给出了子午像距Ss和弧矢像距St随衍射角θ的变化关系，即一阶消像散条件，通过此关系可以消除临近中心波长一定范围的像散。因此，在设计宽波段C-T结构时，需要了解一阶消像散条件对边缘波段的约束能力，从而进一步校正光学系统的像散。

3.2边缘波段像散校正

联立式(4)和式(5)得到光学系统的像散如下：

S(λ)=Ss-St=

(9)

图3　平面光栅与聚焦镜的几何关系图Fig.3　Geometric relations between plane grating and condensing mirror

根据图3所示的坐标系，相应的矢量坐标如下：

AO=(Lgfsinθ,Lgfcosθ),

(10)

(11)

C2O=(-R2sin (θ-α2),R2cos(θ-α2)),

(12)

(13)

由矢量和AO+OC2+C2O′+O′A建立平面光栅与聚焦镜的几何关系，联立式(10)～式(13)得到：

(14)

(15)

联立式(14)和式(15)可得：

(16)

图4模拟了C-T结构全波段像散随波长变化的曲线，可表征光学系统的像散校正能力。模拟过程中，考虑离轴角对C-T结构成像质量的影响，设定准直镜离轴角α1为5°～8°，其余的结构参数相同。图4(a)、4(b)、4(c)、4(d)分别模拟了α取1°,2°,3°,4°，光谱覆盖900～1 700 nm时的像散校正情况。通过观察不同变化关系曲线，可以明显看出α对像散校正能力的影响。

(a)α=1°

(b) α=2°

(c) α=3°

(d) α=4°图4　900～1 700 nm全波段像散随波长变化的曲线Fig.4　Astigmatism versus wavelength over full spectral range of 900～1 700 nm

较小边缘波长到中心波长的波段定义为短波波段(900～1 300 nm)，中心波长到较大边缘波长的波段定义为长波波段(1 300～1 700 nm)。对比图4(a)～4(d)可知，当准直镜离轴角α1相同时，随着α的增大，短波波段的像散校正能力越来越强，长波波段的校正能力越来越弱； 当α相同时，随着准直镜离轴角α1和聚焦镜离轴角α2的同时增大，边缘波段的像散校正能力明显减弱，不过全波段像散的变化趋势相似，离轴角的增大对短波波段像散校正能力的影响较大。

4　实验及结果分析

4.1设计实例

为了验证准直镜离轴角与聚焦镜离轴角的角度差值α对C-T结构边缘波段像散校正能力的影响，分别设计了相同结构参数下，α取不同值时的宽波段C-T结构光学系统，初始结构的基本参数如表1所示。

表1　宽波段Czerny-Turner结构基本参数

对比图4的模拟结果可知，当准直镜离轴角α1=6°时，短波波段和长波波段的像散校正情况合理，因此，这里取α1=6°进行实验仿真和分析。根据初始的基本参数，用Matlab计算出C-T结构的其余参数，将其结果依次导入光学设计软件Zemax中进行光线追迹和设计优化，初始参数和优化参数如表2所示。

表2　宽波段Czerny-Turner结构的设计参数

4.2结果分析

图5给出了α分别取1°，2°，3°和4°时，C-T结构在全波段全视场的RMS值随波长的变化曲线。对比图4(a)～4(d)可知，一阶消像散条件的像散校正能力有限，随着光谱范围的加宽，对边缘像散的约束能力越来越弱；随着聚焦镜离轴角与准直镜离轴角的角度差值α增大，短波波段的像散校正能力增强，长波波段的像散校正能力减弱。

(a) α=1°

(b) α=2°

(c) α=3°

(d) α=4°图5　全波段全视场的点列图Fig.5　RMS spot radii at all wavelengths in full fields of view

由图5可以看出，中心波长处的RMS值不为零，设计结果依然存在一定的弥散斑，主要体现为由球差像差。由于彗差的存在，导致短波波段(900～1 300 nm)与长波波段(1 300～1 700 nm)的弥散斑尺寸不一致。若忽略球差和彗差对光学系统的影响，设计优化结果与理论模拟分析结果的变化趋势基本一致。

为了更全面地说明α值对边缘波段像散校正能力的影响，表3给出了中心视场处中心波长和边缘波长的RMS值。

表3　中心视场处RMS值

为了横向比较不同角度偏差下的像散校正能力，将边缘波长与中心波长的RMS差值进行数据处理，即RMSabsolute(α)=RMSe(α)-RMSc(α)，采用相邻α差值的RMSabsolute(α)比值进行比较分析。图6给出了RMSabsolute(α)与波长的关系曲线。

图6　RMSabsolute(α)随波长的变化曲线Fig.6　RMSabsolute(α) versus wavelength in whole band

在比较分析过程中，定义相邻α值下的RMSabsolute比值为δ，作为评价像散校正能力的标准，具体公式如下：

(17)

根据式(17)可以计算出不同情况下的δ值，比较δ1,δ2,δ3，短波波段的像散校正能力越来越强，像散校正能力平均提高了1.6倍左右；长波波段的像散校正能力越来越弱，像散校正能力平均提高了0.79倍左右，即降低了1.27倍左右。

5　结　论

本文基于发散光束照射平面光栅的像差理论，研究了宽光谱范围下影响像散校正能力的因素，并分析了准直镜离轴角与聚焦镜离轴角的角度差值α和光学系统像散S之间的关系。理论模拟和设计仿真了相同结构参数下，光谱覆盖900～1 700 nm的C-T结构的像散校正情况。实验结果表明，一阶消像散条件对宽波段C-T结构的像散校正能力有限，离轴角增大导致全波段校正能力减弱，边缘波段的像散扩大明显；准直镜离轴角与聚焦镜离轴角的角度差值α不同时，对边缘波段像散的约束能力不同，且随着α逐渐增大。短波波段的校正能力平均提高了1.6倍左右，长波波段的校正能力平均降低了1.27倍左右。这些结论为宽波段光谱仪的像散校正提供了有价值的参考。

[1]陈伟，郑玉全，薛庆生. 机载宽视场大相对孔径成像光谱仪[J]. 光学 精密工程，2015，23(1)：15-21.

CHEN W, ZHENG Y Q, XUE Q SH. Airborne imaging spectrometer with wide field of view and large relative-aperture[J].Opt.PrecisionEng.，2015，23(1)：15-21. (in Chinese)

[2]张晶，王淑荣，黄煜，等. 临边成像光谱仪的发展现状与进展[J]. 中国光学，2013，6(5)：692-700.

ZHANG J, WANG SH R, HUANG Y,etal.. Status and development of limb imaging spectrometer[J].ChineseOptics，2013，6(5)：692-700. (in Chinese)

[3]崔继承，唐国玉，撖芃芃，等. 用于肿瘤手术在线诊断的成像光谱仪的研制[J]. 光学 精密工程，2013，21(12)：3043-3049.

CUI J CH, TANG Y G, HAN P P,etal.. Development of diagnostic imaging spectrometer for tumor on-line operation[J].Opt.PrecisionEng.，2013，21(12)：3043-3049. (in Chinese)

[4]曹海霞，吴娜，冯树龙，等. 单色仪与成像光谱仪的交互光谱定标[J]. 光学 精密工程，2014，22(10)：2586-2591.

CAO H X, WU N, FENG SH L,etal.. Cross-spectral calibration for monochromator and imaging spectrometer[J].Opt.PrecisionEng.，2014，22(10)：2586-2591. (in Chinese)

[5]MASAYUKI F，TAKEHIKO TAKENOUCHI，KEI-ICHI K. Highly efficient and aberration-corrected spectrometer for advanced Raman spectroscope[J].AppliedOptics，2002，41(22)：4655-4665.

[6]XU L，CHEN K X, HE Q SH,etal.. Design of freeform mirrors in Czerny-Turner spectrometers to suppress astigmatism[J].AppliedOptics，2009，48(15)：2871-2879.

[7]SUNG K, THOMPSON K P,ROLLAND J. Broadband antigmatism-corrected Czerny-Turner spectrometer[J].OpticsExperess，2010，18(22)：23378-23384.

[8]QU B X, GUO X,YU F H. Optimization of freeform cylindrical lens in Czerny-Turner spectrometer system to correct the astigmastism by using user defined error function[J].SPIE，2012,8416：84161I.

[9]XUE Q SH. Astigmastism-corrected Czerny-Turner imaging spectrometer for broadband spectral simultaneity[J].AppliedOptics，2011，50(10)：1338-1344.

[10]唐义，张止戈，陈延爱，等. 一种基于柱面反射镜的紫外/可见光成像光谱仪[J]. 光学学报，2013，33(3)：0330004.

TANG Y, ZHANG ZH G, CHEN Y A,etal.. Designed of visible-ultraviolet cylinder mirror imaging spectrometer[J].ActaOpticaSinica, 2013，33(3)：0330004. (in Chinese)

[11]AUSTIN D R，WITTING T，WALMSLEY I A. Broadband astigmatism-free Czerny-Turner imaging spectrometer using spherical mirrors[J].AppliedOptics，2009，48(19)：3846-3853.

[12]BATE B，DOWELL M，NEWTON A C. Correction of astigmatism in a Czerny-Turner spectrograph using a plane grating in divergent illumination[J].J.Phys.，1970，E3(3)：206-210.

董科研(1980-)，男，吉林长春人，博士，副教授，主要从事激光通信及光学系统设计方面的研究。E-mail: dongkeyan@163.com

李欣航(1991-)，女，吉林长春人，硕士研究生，2010年于长春理工大学获得学士学位，主要从事光学系统设计方面的研究。Email: 317554403@qq.com

(版权所有未经许可不得转载)

Influence factors of Czerny-Turner edge band astigmatism correction

DONG Ke-yan1, LI Xin-hang1,2*, AN Yan1

(1.Institute of Space Photoelectric Technology, ChangchunUniversityofScienceandTechnology，Changchun130022,China；2.Opto-electronicsEngineerInstitute,ChangchunUniversityofScienceandTechnology，Changchun130022，China)*Correspondingauthor,E-mail: 317554403@qq.com

To improve the weak correcting capacity of a wide band Czerny-Turner structure, the influence factors on the astigmatism correction of an optical system were analyzed. The Matlab software was used to simulate and analyze the reasons that the astigmatism was produced and the traditional method could not suppress the astigmatism. Then, the dependence of the angle differenceαbetween the off-axis angle of collimator mirror and the off-axis angle of focusing mirror on the astigmatismSof the optical system was discussed. The astigmatism correction of wide band Czerny-Turner structure was simulated at differentαvalues. To verify the validity of the theoretical analysis, an astigmatic Czerny-Turner system ranging from 900 to 1 700 nm was designed, the Zemax was used to perform the ray tracing and optimal design and the design results were processed and analyzed. The simulation results demonstrate that the shortwave band astigmatism correction ability is getting stronger with increasing the difference angle, which may achieve about 1.6 times on increase. However, long wave band astigmatism correction ability is more and more weak, which may reduce about 1.27 times on average. It suggests that the reasonable selection of the difference angle can provide the theoretical guidance for correcting the astigmatism of wide band Czerny-Turner structures.

optical design; Czerny-Turner structure; astigmatism correction; edge band

2016-05-31；

2016-06-30.

长春市科技局科技支撑计划资助项目(No.14DR003);校内青年科学基金资助项目(No.XQNJJ-2013-12);吉林省教育厅“十三五”科学技术研究项目(吉教科合字[2016]第368号)

1004-924X(2016)10-2384-08

O435.1；TH703

Adoi:10.3788/OPE.20162410.2384