时间序列以及卡尔曼滤波在电力系统短期负荷预测中的应用

张楷楷，燕萍

(1.内蒙古电力勘测设计院有限公司，内蒙古　呼和浩特　010020 ； 2.国网湖北省电力公司鄂州供电公司，湖北　鄂州　436000)



时间序列以及卡尔曼滤波在电力系统短期负荷预测中的应用

张楷楷1，燕萍2

(1.内蒙古电力勘测设计院有限公司，内蒙古呼和浩特010020 ； 2.国网湖北省电力公司鄂州供电公司，湖北鄂州436000)

随着电力系统的发展，电力市场的产生以及新能源的引入带来的负荷的随机性和周期性给电力系统短期负荷的预测带来了一定的难度。本文就电力系统短期负荷的预测模型进行分析，采用了时间序列模型和卡尔曼滤波模型，并针对负荷的数量的不同采用不同的模型，进而用Eview软件和matlab程序做相应的仿真和验证。最后得出，若是负荷数量比较少时，利用时间序列比较简单；若是负荷数量比较多时，采用卡尔曼滤波比较精确。

短期负荷预测；时间序列；卡尔曼滤波；Eview软件；matlab程序

1　引言

为用户提供优质、稳定的电能是电力系统的主要任务，而实现该任务的前提是电力运行、调度和规划部门必须要掌握用户的用电规律和变化趋势。同时，自2002年我国实行“厂网分离”以来，我国电力工业正在逐步过渡到市场化进程。负荷预测是各企业了解用户的用电需求、规律和变化趋势的有力工具[1]。

电力负荷一般是指电力需求量或用电量，或者说成是电力系统中所有使用电能的用电设备在某一时间段所消耗的电功率之和。根据负荷的使用时间的不同，负荷预测可以分为长期负荷预测、中期负荷预测、短期负荷预测和超短期负荷预测[2]。

短期负荷预测的核心问题是依据负荷特性，选择合适的负荷预测模型。对于短期负荷的预测模型，国内外学者提出了一系列的研究方法。

文献[3]提出的相似日法是利用某种差异评价函数寻找某些与预测日负荷特征相似的某些历史日，将这些相似日的负荷根据预测日的负荷参数进行修正，从而得出预测日的负荷，在精度上的要求很低。

灰色理论是20世纪80年代初由我国著名学者邓聚龙教授提出来的，并用于描述部分信息已知的系统[4-5]。目前在电力负荷预测较常使用的是GM(1，1)模型，首先通过采用灰色生成技术处理少量的历史负荷数据，再采用一阶微分方程来拟合灰色生成后的数据，最后用该一阶微分方程的解进行负荷预测[6]。

时间序列法通过分析历史负荷数据信息，建立数学模型，反映随机变量变化过程中的规律性，进而确定数学表达式，对未来负荷进行预测[7]。

卡尔曼滤波法又称为状态空间法，对历史数据进行滤波估计，得到系统下一个时刻状态的最佳估计，通过预测获得新数据反映了系统的未来状态。因此它们的组合能够让预测模型获得更多的信息，得到更加准确的预测值[6]。

随着现代科学技术的发展，负荷预测技术得到了极大的发展。人工神经网络、支持向量机、混沌理论[8-11]、专家系统[12-15]、模糊理论[16-18]和小波分析[19-22]等理论成功地引入到负荷预测领域。

本文就采用时间序列和卡尔曼滤波对电力系统负荷进行仿真和验证，最后提出对于数量较少的负荷可以采用软件Eview和matlab程序的时间序列结合来预测电力系统负荷，先用软件Eview对数据进行平稳性处理，在平稳性处理的基础上利用matlab程序对数据进行预测；当负荷数量较多时，采用卡尔曼滤波比时间序列模型更精确。

2　时间序列预测电力负荷

时间序列被认为是最经典的、最系统、最被广泛采用的一类短期负荷预测方法[23]。时间序列法可以分为自回归过程AR(p)，滑动平均过程MR(q)，自回归滑动平均过程ARMA(p，q)等。

2.1平稳时间序列一个随着t变化的量{yt}在t1,t2,t3…tN…的观测值为：

y(t1),y(t2),y(t3)…y(tN)…

组成的有序的离散的集合，则称为时间序列，简记为{yt}。

2.1.1平稳性原理

如果一个随机过程的均值和方差在事件过程上均为常数，并且任意两时期之间的协方差依赖于该两时期的距离，而不依赖于计算这个协方差的实际时间[23]，即

(1)

式子(1)对于所有的t均成立，其中ρk相隔k个单位的两随机变量之间的协方差，只与k有关而与t无关。

如果时间序列满足式子(1)，则称为平滑时间序列。若是非平稳序列，一般通过差分处理来消除数据的不稳定性。先对数据序列进行差分，然后对差分数据进行回归。但这样会丢失数据的长期信息，而这些数据对于数据的分析又是非常重要的，这就是时间序列检验两难的问题。

2.1.2时间序列的平滑性检验

ADF检验是统计学中一个普遍的检验方法[24]，在对时间序列进行平稳性检验的时候，更加准确和重要。ADF检验主要是通过以下模型进行的[25]：

(2)

其中t为时间变量，α为常数，βt为趋势项，εt为残差项。原假设都是H0∶δ=0，若检验拒绝H0∶δ=0即原序列不存在单位根，为平稳序列，即可停止检验。

2.2时间序列的模型种类

2.2.1AR模型

在短期负荷预测研究中，引起负荷变化的因素很多，不可能把影响负荷的因素都一一归入模型。从各级调度部门可获得的是过去历史的负荷记录，易于得出某一时刻的负荷与它过去相关时刻的负荷有关。AR模型中的基本概念为：因变量是待测的负荷，而自变量则是负荷自身的过去值。AR的过程为：现在值可由过去值的加权值的有限线性组合及一个干扰量at

yt=φ1yt-1+φ2yt-2+…φpyt-p+at

(3)

式中为模型阶数，φ1，φ2…φp为模型参数，yt-1，yt-2…yt-p为历史数据，干扰量at为白噪声序列在t时刻的值，模型的阶数p和系数φ1，φ2…φp由过去负荷值通过模型辨识和参数估计来确定。

白噪声at的性质(对所有t均成立)

(4)

因为测的负荷与它过去时刻的负荷有关，故称为AR模型。

2.2.2MA模型

在AR模型中，理论上干扰的影响是在无限长的时间内存在的，即一个初始时刻的干扰将会影响到未来无限长时间内的负荷值[23]。假设干扰的影响在时间序列中只表现在有限的几个连续时间间隔内，然后就完全消失，获得派生模型，即为MA模型。

若初始时刻的干扰仅在前q步内有影响，则q阶模型为：

yt=at-θ1at-1-θ2at-2…-θqat-q

(5)

式中，为模型阶数，θ1，θ2…θp为模型参数。

2.2.3ARMA模型

ARMA模型即为AR模型和MA模型的组合，表达式为

yt=φ1yt-1+φ2yt-2+…φpyt-p+at-θ1at-1-θ2at-2…-θpat-q

(6)

当p=0时即为MA模型，当q=0时，即为AR模型。综上所述，AR和MA时ARMA的特例。

2.3时间序列的自相关系数和偏相关系数

对模型预测而言，先要找到与其拟合度最高的预测模型，其次建立模型的关键还在于模型阶数的确定和参数的估计。由序列的自相关函数、偏自相关函数初步判断时间序列是否平稳，再进一步判定模型种类、模型阶数，最后用信息准则检验模型的适用性(确定阶数)[25]。

2.3.1自相关系数

构成时间序列的每个序列值xt,xt-1…xt-k之间的简单相关关系称为自相关[1]。

自相关系数可以用来度量自相关程度，它表示在一个时间序列中，观测值之间在相隔k期时的相关程度。

(7)

(8)

(9)

(10)

化简公式(9)～(12)可得自相关系数的表达式

(11)

2.3.2偏相关系数的求解

对于平稳序列{xt}所谓滞后k偏自相关系数就是指在剔除了中间k-1个随机变量xt-1，xt-2…xt-k+1的情况下，xt-k对xt的影响。偏相关的估计值为[1]

(12)

2.4模型的辨识和参数估计

2.4.1模型辨识

模型的辨识即为确定模型的阶数，基本途径就是对时间序列进行分析，即计算时间序列的均值，自相关系数，偏相关系数，从而确定模型的阶数。

由自相关和偏相关的“拖尾”和“截尾性”可知，p阶开始的所有偏相关系数均为0；从q阶开始的所有自相关系数均为0[25]。

图1　数据的偏相关，自相关系数图

由图1分析可知，偏相关系数在k=2阶的时候为0，即在2阶截尾，因此可以确定p=1；自相关系数呈现周期性，无法判断q的值，因此确定为AR(2)。

同样在利用matlab程序数据进行处理，通过残差方差的大小和AIC的值来确定AR的阶数。

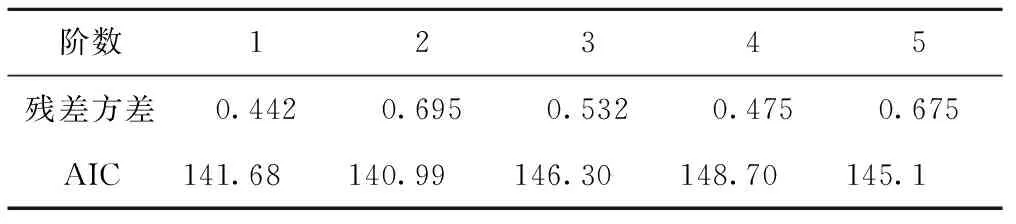
表1　matlab程序中阶数与残差方差以及AIC

综上所述，AR模型的阶数为p=2。

2.4.2参数的估计

利用matlab程序对数据进行处理，得出相关的表达式即

yt=0.614yt-1+0.053125yt-2+0.0616yt-3+a(t)

2.5模型的检验

用相关图检验拟合后的残差是否为白噪声[26]。若是，则模型合理。因为白噪声过程是序列无关的，所以白噪声过程的自相关函数和偏相关函数在相关图中均为零。

利用Eview软件作出残差的自相关和偏相关关系图，如图2所示。

由图2分析可知，残差的自相关系数基本上为0，因此预测模型有效。

利用matlab程序运行残差的自相关系数的结果为=-0.0884，接近于0。因此，模型的拟合是符合要求的。

图2　残差的偏相关，自相关系数图

2.6模型的预测

在Eview软件中静态预测是利用滞后因变量的实际值而不是预测值计算一步向前预测的结果；动态预测是从样本的第一个数据开始计算多步预测，因此静态预测比动态预测更精确，因此在本次仿真中采用静态预测。在图3中显示预测曲线以及加减两个标准差的带状域。

图3　Eview软件的预测曲线

分析图3可知，预测值位于实际值的95%置信区间内，数据的预测值和实际值以及相对误差如表2所示。

表2　Eview软件中实际值，预测值以及相对误差

在matlab程序中仿真的预测值以及预测曲线如表3和图3所示。

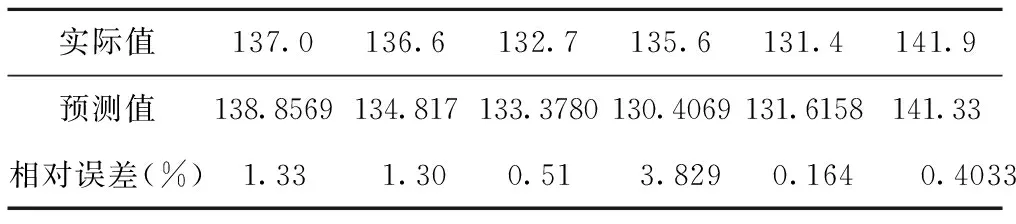
表3　matlab中程序实际值，预测值以及相对误差

时间序列法的优点是所需数据少，工作量较小，计算速度较快，不需要人工干预，可自动进行预测，能够反映负荷变化连续性特点。缺点是对原始负荷时间序列的平稳性要求过高，在数据不平滑时需要对数据进行平滑性处理，破坏了数据信息的完整性，当数据量比较多时，可以采用卡尔曼滤波[27]。

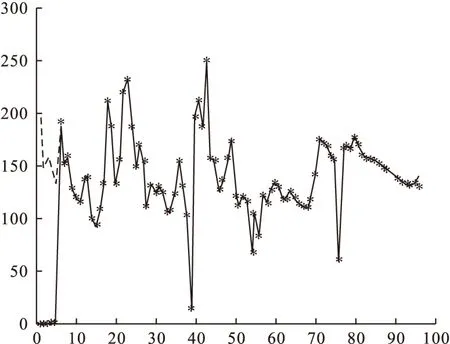
图4　matlab程序预测曲线

综上所述流程图如图5所示。

图5　时间序列预测电力系统负荷流程图

3　卡尔曼滤波预测电力系统负荷

卡尔曼是一种高效递归滤波器，它能够从一系列完全包含噪声的测量中，估计系统的状态。基本思想是：采用信号和噪声的状态空间模型，利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计，求出现时刻的估计值，再结合现时刻的量测值求出现时刻的最优值[28]。

卡尔曼滤波法应用于预测，被估计系统为以下的离散时间系统如式子(13)所示：

X(k+1)=A(k+1,k)X(k)+ω(k)

(13)

系统的观测值方程如式子(14)所示：

y(k+1)=H(k+1)X(k+1)+υ(k+1)

(14)

式中：y(k+1)为k时刻的测量值向量；X(k)为状态变量；H(k+1)为k+1时刻的预输出观察矩阵；A(k+1,k)表示从k～k+1的状态转移矩阵；ω(k+1)和υ(k+1)分别为系统和测量过程的白噪声。

在本文中，假定系统噪声ω(k)和测量噪声υ(k)是互不相关的，且均值为零的噪声序列，即对所有的k有：

(15)

式中：系统噪声协方差矩阵为Q和测量噪声协方矩阵R为均是对称正定的。

(16)

对y(k+1)的预测估计为：

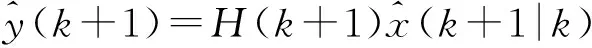
(17)

(18)

(19)

P(k+1|k+1)=[I-K(k+1)H(k+1)]P(k+1|k)

(20)

式中：K为卡尔曼增益，K必须使P(t+1)均方误差为最小，即TrP(t+1)=min，根据均方误差最小。可以推得：

K(k+1)=P(k+1|k)HT(k+1)[H(k+1)P(k+1|K)HT(k+1)+R(k)]-1

(21)

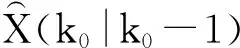
基于卡尔曼滤波法的电力系统负荷的预测中，考虑了在同一时间段上过去三天内负荷，还考虑了现在同一天内三个时段的负荷。

负荷预测模型可表示为：

T(k+1)=C0T0(k)+C1T1(k+1)+C2T2(k+1)+C3T3(k+1)+υ(k)

(22)

式中：C0,C1,C2,C3为参数矩阵，Ci=[ci,1(k),ci,2(k),ci,3(k)]

Ti(k)=[ti(k),ti(k-1),ti(k-2)]T为前i天第k、k-1、k-2时段电力系统负荷；T(k+1)为预测负荷；υ(k)为观测噪声。

y(k)=T(k)

利用时间序列原理编写matlab程序，对579[28]个数据进行预测结果分析。

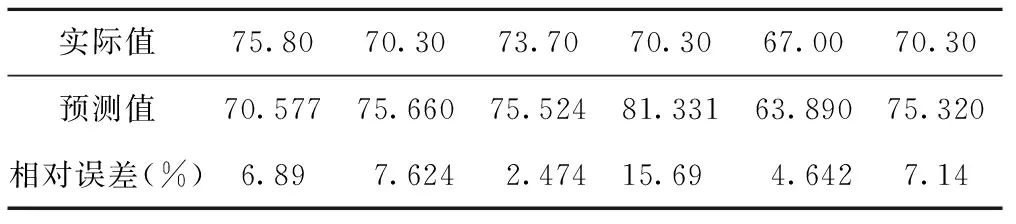
表4　实际值与预测值以及相对误差分析

利用卡尔曼滤波原理编写的matlab程序对579个数据进行预测结果分析

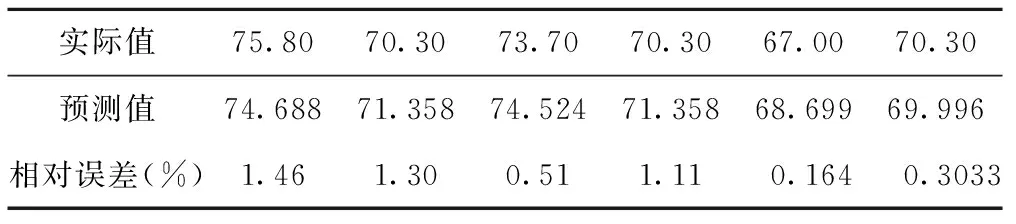
表5　实际值与预测值以及相对误差分析

综上所述，当数据比较少时，采用时间序列来预测电力系统负荷；当数据比较多时，采用卡尔曼滤波来预测，可以提高数据预测的精确度。

4　总结

近年来风力发电和光伏发电的迅速发展，由于其波动性、间歇性的特点，大规模并网发电将对电网产生冲击。为实现电力系统的安全经济调度，急需更加准确可靠的电力负荷预测方法，为适应这种现状，急需对传统的负荷预测方法进行改进。与此同时，电力系统的市场化是电力系统发展的必然趋势，电力系统的市场化必然伴随着商家对经济利益的追寻，而负荷预测是各企业了解用户的用电需求、规律和变化趋势的有力工具。本文就采用Eview软件和matlab程序针对电力系统负荷进行预测利用ARMA模型时间序列和卡尔曼滤波的方法，并得出相应的误差分析。两个实例证明，当数据量比较小的时候，可以采用Eview软件或时间序列进行预测，当数据量比较大时，利用卡尔曼滤波的方法得到的误差比较小。

[1]李晗书.时间序列分析在电力负荷预测中的应用研究[D].燕山大学，2009.

[2]徐军华.电力系统短期负荷预测模型与优选的研究[D].四川大学,2004.

[3]关薇.时间序列在电力系统负荷预测中的应用[D].北方工业大学,2010.

[4]邓聚龙.灰色预测与决策[M].华中理工大学出版社,1988.

[5]张俊芳，吴伊昂，吴军基.基于灰色理论负荷预测的应用研究.电力自动化设备，2004，24(5):24-27.

[6]吴慢红，杨继旺.几种电力负荷预测方法及其比较[J].广东电力,2004，17(1):17-21.

[7]马静波.电力系统短期负荷预测方法研究[D].四川大学,2005.

[8]SeijinKawauchi,Hiroaki Sugihara,Hiroshi Sasaki.A development of very short-term load forecasting based on chaos theory[J].IEEJ Trans.PE，2003，123(5):646-653.

[9]陆毅宏，韩文秀，张伟波.基于关联度的混沌序列局域加权线性回归预测法[J].中国电机工程学报，2004，24(11)：17-20.

[10]蒋传文，袁智强，候志俭，等.高嵌入维混沌负荷序列预测方法研究[J].电网技术，2004，28(3)：25-28.

[11]温权，张勇传，程时杰.负荷预报的混沌时间序列分析方法[J].电网技术，2001，25(10)：13-16

[12]Rahman S，Bhatnagar R.An expert system based algorithm for short term load forecasting[J].IEEE Trans on Power System,1988,3(2):392-399.

[13]夏道止，王锡凡，周琳，等.基于 RBF 神经网络和专家系统的短期负荷预测方法[J].西安交通大学学报，2001，35(4)：331-334.

[14]朱向阳，林鹤云.一种基于 RAN 和专家系统的短期负荷预测方法[J].华东电力，2004，32(9)：42-44.

[15]甘文泉，王朝晖，胡保生.结合神经元网络和模糊专家系统进行电力短期负荷预测[J].西安交通大学学报，1998，32(3)：28-32.

[16]Mori H，Kobayashin H.Optimal fuzzy inference for short-term load forecasting[J].IEEE Transactions on power Systems,1996，11(1):390-396.

[17]张昊，吴捷，郁滨.电力负荷的模糊预测方法[J].电力系统自动化，1997，21(12)：11-14

[18]Senjyu T,Mandal P，Uezato K,et al.Next day load curve forecasting using hybrid correction method[J].IEEE Transactions on Power Systems,2004，99(99):1-8

[19]冉启文，单永正，王骐，等.电力系统短期负荷预测报的小波-神经网络-PARIMA方法[J].中国电机工程学报，2003，23(3)：38-42.

[20]徐军华，刘天琪.基于小波分解和人工神经网络的短期负荷预测[J].电网技术，2004，28(8)：30-33.

[21]杨延西，刘丁.基于小波变换和最小二乘支持向量机的短期电力负荷预测[J].电网技术，2005，29(13)：60-64.

[22]甘文泉，王朝晖，胡保生.结合神经元网络和模糊专家系统进行电力短期负荷预测[J].西安交通大学学报，1998，32(3)：28-32

[23]周潮，邢文洋，李宇龙.电力系统负荷预测方法综述[J].电源学报,2013(6):32-39.

[24]莫达隆.利用ADF检验对时间序列进行建模[J].时代金融,2010,4:025.

[25]于宁莉，易东云，涂先勤.时间序列中自相关与偏相关函数分析[J].数学理论与应用,2007,27(1):54-57.

[26]康重庆，夏清，张伯明.电力系统负荷预测研究综述与发展方向的探讨[J].电力系统自动化，2004，28(17):1-11.

[27]潘迪夫,刘辉,李燕飞.基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J].电网技术,2008,32(7):82-86.

[28]马静波，杨洪耕.自适应卡尔曼滤波在电力系统短期负荷预测中的应用[J].电网技术，2005，29(1):75-79.

燕萍(1989.11-)工程师，研究方向：电力系统运行。

Application of Time Series and Kalman Filtering in Short-term Load Forecasting of Power Systems

ZHANGKai-kai1，YANPing2

(1.Znner Mongolla Electric Power Prospecting Design Institute Co.,Ltd,Hohhot 010020,China;2.Ezhou Power Supply Bureau,Hubei State Grid,Ezhou 436000,China)

With the development of power system，the generation of electricity market and the introduction of new energy lead to the load more randomness and periodic which has brought certain difficulty to the forecast of short-term load of power system.In this paper,the power system short-term load forecasting models are analyzed，adopting the time series model and Kalman Filtering Model.And the different models applied according to the number of loads.In this paper,Eview software and matlab are to do simulation and verification accordingly.In conclusion,if the load quantity is small,the use of time series is simple;if the load quantity is large,using Kalman filtering is accurate.

short-term load forecasting;time series;kalman filtering;Eview software;matlab order

1004-289X(2016)02-0091-06

TM71

B

2015-12-03

张楷楷(1986.04-)工程师，研究方向：电力系统运行；