高精度滚珠丝杠最佳接触角的分析与验证

陈婉，王科社，宋杰，董青霞

北京信息科技大学，北京，100192

高精度滚珠丝杠最佳接触角的分析与验证

陈婉，王科社，宋杰，董青霞

北京信息科技大学，北京，100192

接触角作为滚珠丝杠副的重要结构参数之一，对其性能有着重要影响。研究表明，接触角越大，滚珠丝杠的承载能力越大，但过大的接触角会加大接触变形从而影响精度。随着滚珠丝杠副不断向着高速高精发展，对高精度滚珠丝杠副接触角的研究就显得尤为重要。结合滚珠丝杠副接触角对丝杠转速的影响，分析接触角与滚珠丝杠副旋滚比及摩擦力矩的关系，总结出高精度滚珠丝杠副最佳接触角的选取范围，并以某型号滚珠丝杠副为例，通过分析计算得出其最佳接触角，进而运用有限元软件分析理论最佳接触角与通常采用的45°接触角下滚珠丝杠副的应力应变分布，验证了理论最佳接触角变形小精度高的结论。

滚珠丝杠；接触角；精度；有限元分析

0 前言

滚珠丝杠副是数控机床重要的功能部件，而接触角作为滚珠丝杠副的重要结构设计参数之一，对于滚珠丝杠的传动性能有很大的影响。实际工程当中，滚珠丝杠副的受力情况、使用条件及型号等可变因素使得最佳接触角的值存在不确定性，且滚珠丝杠在工作过程中会产生变形，从而导致实际接触角与理论值有一定偏差。研究表明，接触角越大，滚珠丝杠的承载能力就越大，但过大的接触角会降低滚珠丝杠副的精度，所以综合各项因素，通常采用的接触角为45°。在对于滚珠丝杠副高精度的要求不断提高的大背景下，研究滚珠丝杠副负载小、精度要求高时的最佳接触角就显现出重要意义。

目前国内外对于高精度滚珠丝杠副最佳接触角的研究还比较少，就国内而言，北京信息科技大学李晓［1］通过研究滚珠受力情况，分析了接触角对丝杠转速及接触变形的影响，得出最佳接触角应小于40°的结论。本文在此基础上，从接触角对旋滚比及摩擦力矩的影响出发，分析计算理论上的最佳接触角的选取范围，并以某型号滚珠丝杠副为例，分析计算出其保证高精度情况下的最佳接触角，进而将其与通常采用的45°接触角进行比较，运用有限元软件进行应力应变分析。

1 最佳接触角的理论分析

接触角对滚珠丝杠的性能有很大的影响，由滚珠丝杠的结构特点可知，接触角与滚珠丝杠的承载能力呈正比，接触角越大，系统的承载能力就越大，而且传动的效率也越高，但是在轴向力相同的作用下，当接触角变大时，径向力也会变大，从而降低了滚珠丝杠的使用寿命。［2］本章结合相关文献从接触角对滚珠丝杠副的旋滚比及摩擦力矩的影响等方面进行分析，确定低载高精滚珠丝杠副最佳接触角的选取范围。

1.1 接触角对滚珠旋滚比的影响

接触角的存在不但能够使滚珠沿着螺旋滚道运动，并且能使滚珠产生自旋运动。滚珠的自旋运动影响着系统的摩擦力矩，自旋运动程度越小，因自旋产生的摩擦力矩就越小。滚珠旋滚比是指滚珠自旋的角速度与沿螺旋滚道的角速度的比值。旋滚比的大小反映了滚珠自旋运动的程度，其值越小，滚珠自旋运动的程度就越小。［3］

分析过程中首先选取适当坐标系，在不考虑陀螺效应的情况下，若螺旋升角为零，则滚珠与螺母滚道接触处的旋滚比Sxg可参照角接触球轴承的分析方法得到，其旋滚比的计算公式如下：

由上式可知，滚珠直径、丝杠公称直径等都会影响最佳接触角的大小。本文以DS4716型号的滚珠丝杠副为例，根据式（1.1）、（1.2），在MATLAB中编写程序，做出接触角对旋滚比的影响曲线，如图1所示。

编写程序如下：

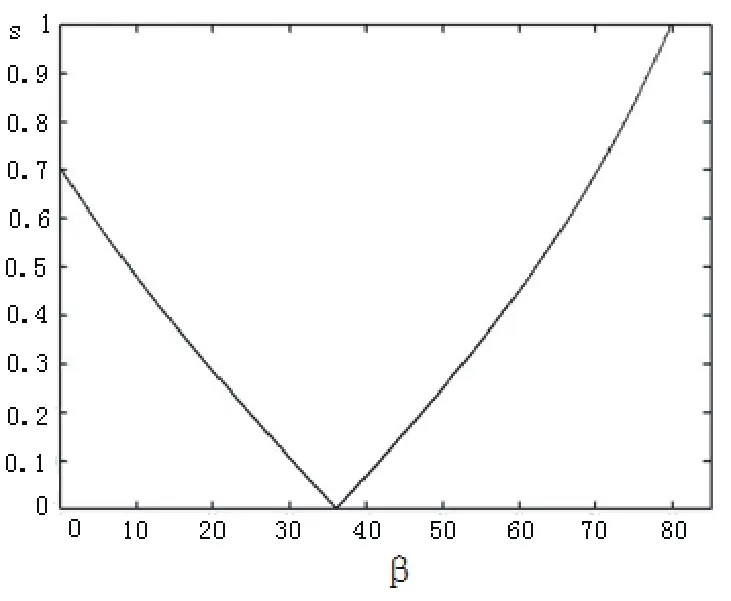
从图1可以看出，接触角β对旋滚比的影响很大，当β=37º时，旋滚比达到最小，此时滚珠自旋运动的程度最小，由自旋所产生的摩擦力矩也最小，传动效率最高。

取南通友谊机械制造公司G.GD系列，型号1604-3到5012-4滚珠丝杠副的db、d、t值，进行多次MATLAB分析发现最佳接触角的位置在30°与40°之间变化。

1.2 接触角对摩擦力矩的影响

摩擦力矩的大小对滚珠丝杠的温升、精度等有重要影响。本文根据康献民［4］得出的滚珠丝杠副摩擦力矩计算公式，在接触角从30°到50°中等间隔取10个值，并以DS4716型号的滚珠丝杠副为例，计算出相应的摩擦力矩，结果如表1所示。

根据表1中所得出的数据，用Origin 拟合出摩擦力矩与接触角的关系曲线，如图2所示。

由图2可以看出，滚珠丝杠副的摩擦力矩随接触角变化比较复杂。对于DS4716滚珠丝杠副，当接触角逐渐增大时，摩擦力矩的数值往复变化，但在37°附近，产生的摩擦力矩最小，滚珠丝杠的效率最高。

由摩擦力矩公式可知，丝杠副中丝杠的螺旋升角、导程等以及滚珠直径都会影响曲线最佳接触角的位置。由于G.GD系列滚珠丝杠副各零件尺寸已包含极限尺寸，所以以此得出的最佳接触角选取范围具有普遍性。与分析旋滚比时相同，取型号1604-3到5012-4滚珠丝杠副，计算其接触角在30°到50°的摩擦力矩值，发现摩擦力矩最小值出现在接触角30°与40°之间。

通过以上分析，结合文献中对最佳接触角与转速关系的研究得出最佳接触角的选取范围为30°到40°。以DS4716滚珠丝杠为例，总结其性能随接触角的变化情况如下表所示。

表1 接触角与摩擦力矩Tab.1 Contact angle and friction torque

图2 接触角与摩擦力矩的关系曲线Fig. 2 Curve of contact angle and the friction torque

2 最佳接触角的仿真分析

前面通过理论分析得出DS4716型号滚珠丝杠副在追求高精度时的最佳接触角为37°，但通常在加工设计时选用的接触角为45°。用ANSYS分析两种接触角下滚珠丝杠副的应力应变情况，从而进一步验证理论最佳接触角在变形小精度高等方面的优越性。

2.1 滚珠丝杠副三维模型的建立

本章要分析不同接触角情况下滚珠丝杠副的受力与变形就必须建立仅接触角不同的滚珠丝杠三维模型。首先建立滚珠丝杠副滚道坐标系，从坐标系中可以推导出下列公式：

由上式看出，可以通过改变滚珠的半径来改变接触角的大小，从而建立仅接触角不同的滚珠丝杠三维模型。

根据精密天工有限公司提供的DS4716型号滚珠丝杠副的图纸，运用Pro/E建立三维模型如图3所示。

2.2 常用接触角的滚珠丝杠副有限元分析

模型建立完成后，将其导入ANSYS分析软件中，设置静态结构分析项，进行静力学分析。

通过仿真分析，求解出接触角为45°时滚珠丝杠副的滚珠及整体系统的应力和应变云图如图4、图5所示。

通过ANSYS分析结果可知：系统等效应力的主要集中区域是滚珠与滚道接触区，且螺旋滚道里的滚珠受到的应力基本相同。由于滚珠与滚道的接触面积非常小，相同压力下，滚珠受到的接触应力则比较大。本文主要给出滚珠及整体系统的应力应变云图，具体的各零件应力应变数值记录在表3、4中。

2.3 理论最佳接触角的滚珠丝杠副有限元分析

对最佳接触角的丝杠模型进行仿真分析时，根据45°接触角模型的分析方法进行网格划分以及载荷和约束的添加，在受力、材料等其他条件相同的情况下有限元分析的应力和应变结果如图6、图7所示。

表3 各零件最大接触应力（MPa）对比Tab.3 Comparison of maximum contact stress （MPa） of each part

表4 各零件最大应变量（μm）对比Tab.4 Comparison of the maximum stress （μm） of each part

图3 滚珠丝杠副三维模型Fig. 3 Ball screw pair's 3 d model

图4 接触角 45°的滚珠丝杠等效应力图Fig. 4 Equivalent stress of ball screw with contact angle of 45°

图5 接触角45°的滚珠丝杠等效应变图Fig. 5 Equivalent effect of ball screw with contact angle of 45°

图6 接触角 37°的滚珠丝杠等效应力图Fig. 6 Equivalent stress of ball screw with contact angle of 37°

图7 接触角 37°的滚珠丝杠等效应变图Fig. 7 Equivalent effect of ball screw with contact angle of 37°

由图6、图7可得出接触角为37°时滚珠及整体系统的应力应变情况，同理各零件最大应力值及最大应变量记录在表3、4中。

2.4 不同接触角的滚珠丝杠副仿真结果比较

根据上述分析结果，将接触角为45°和37°的滚珠丝杠进行对比，可得各零件的最大接触应力值及最大应变量如表3、4所示：

通过表3、4的对比结果可以看出，对于DS4716型滚珠丝杠副，在施加相同的载荷和约束的情况下，接触角分别为45°和37°时，滚珠丝杠副中滚珠的接触应力相差较大，螺母、丝杠的最大应力和最大应变量相差并不大，忽略分析误差，可以得出相同工况下，接触角为37°时，滚珠丝杠副的变形更小，精度更高。

3 结束语

由于滚珠丝杠副型号、使用条件等的不同，最佳接触角将不是一个固定值。本文分析了接触角β对滚珠丝杠副旋滚比和摩擦力矩的影响，通过MATLAB和Origin工具进行编程，得出相应的影响曲线，综合各影响因素，确定高精度低负载滚珠丝杠副最佳接触角的范围，并以DS4716型号的滚珠丝杠副为例，分析计算出其最佳接触角为37°。进而分别建立37°最佳接触角与通常采用的45°接触角下滚珠丝杠副的三维模型，用ANSYS分析两种接触角下滚珠丝杠副的应力和应变的分布情况，发现其他条件相同时，37°的滚珠丝杠副滚珠的最大接触应力比45°的小很多，从而验证采用理论最佳接触角比采用45°接触角变形小，精度高。本文通过数值分析及有限元验证的方法进行研究，由于分析计算的变量尺寸包含极限尺寸而具有普遍性，得出的结论有助于高精度滚珠丝杠副的发展，对其他型号滚珠丝杠副最佳接触角的研究有指导意义。

［1］ 李晓.高性能滚珠丝杠副理论研究与仿真分析［D］. 北京：北京信息科技大学.2014

Li Xiao. Theoretical research and simulation analysis of high performance ball screw ［D］. Beijing：Beijing Information Science and Technology University.2014.

［2］ 张佐营. 高速滚珠丝杠副动力学性能分析及其实验研究［D］. 济南：山东大学，2008.

Zhang Zuoying. Dynamic performance analysis and experimental study of high speed ball screw rod ［D］. Jinan：Shandong University，2008.

［3］ 许向荣.单螺母滚珠丝杠副轴向刚度的分析研究［J］.武汉理工大学学报，2009，31（24）：54-57.

Xu Xiangrong. Single nut ball screw pairs to analysis stiffness［J］. Journal of Wuhan University of Technology，2009，31 （24）：54-57.

［4］ 康献民.精密滚珠丝杠副摩擦力矩波动的分析与测试［J］.中国机械工程［J］.2010，21（4）：400-405..

Kang Xianmin. Analysis and testing of the friction torque fluctuation of precision ball screw pairs ［J］. China Mechanical Engineering ［J］.2010，21 （4）：400-405.

［5］ T.A.Harris，M.N.Kotzalas.滚动轴承分析［D］.机械工业出版社，2010..

T.A.Harris，M.N.Kotzalas. Rolling bearing analysis ［D］. The Journal of Machinery Industry，2010.

［6］ 赵训贵.滚珠丝杠副产生弹性变形时实际接触角的计算［J］.机床.1989.

Zhao Xungui. Calculation of the actual contact angle of the ball screw pair to produce elastic deformation ［J］. Machine Tool.1989.

［7］ 李东君.滚珠丝杠副接触变形的有限元分析［J］.机械传动，2010，34（12）：34-36.

Li Dongjun. Finite element analysis of contact deformation of ball screw pairs ［J］. Mechanical Transmission，2010，34 （12）：34-36.

［8］ 刘晓慧.滚珠丝杠副摩擦力矩影响因素及测试方法研究［D］.济南：山东大学.2006.

Liu Xiaohui. Study on influence factors and testing methods of friction torque of ball screw pairs ［D］. Jinan：Shandong University.2006.

［9］ Wei C C，Liou W L，Lai R S. Wear analysis of the offset type preloaded ball-screw operating at high speed［J］. Wear，2012，292：111-123.

［10］ 周忆，张恒，刘芳.平板型水润滑橡胶轴承摩擦噪声的有限元分析［J］.新型工业化，2013，3（10）：67-72.

ZHOU Yi，ZHANG Heng，LIU Fang.The Finite Element Analysis of Friction-induced Noise For Plate Type Water-lubricated Rubber Bearing［J］.The Journal of New Industrialization，2013，3（10）：67-72.

［11］ 王诗，王浩童，李小兵，等.基于加热源位置的温度控制算法的研究［J］.新型工业化，2014，4（5）：69-76.

WANG Shi，WANG Haotong，LI Xiaobing，et al .Studies on Temperature Control Algorithm Based on The Heat Producer Position［J］.The Journal of New Industrialization，2014，4（5）：69-76.

Analysis and Verification of the Best Contact Angle in Ball Screw

CHEN Wan， WANG Ke-she， SONG Jie， DONG Qing-xia
（Beijing Information Science & Technology University， Beijing， 100192）

Contact angle as one of the important structure parameters of ball screw pair， has an important influence on its performance. Researches show that the bigger the contact angle is， the greater the carrying capacity of the ball screw pair is， but too big contact angle will increase contact deformation and affect precision. With the development of ball screw pair towards high speed and high precision， the study of high precision ball screw pair's contact angle is particularly important. Combining with the contact angle of ball screw pair on the influence of screw speed， etc， the relationships between contact angle and the ratio of revolution and rolling and the friction torque were analyzed， summed up the best range of contact angle of the high precision ball screw pair. Take a type screw pair for example， it is concluded that the best contact angle of this ball screw pair and then by using the finite element analysis software analyze the stress and strain distribution of the theory best contact angle and the usually adopted 45° contact angle of ball screw pair， coming to a conclusion that the deformation of the theory contact angle is small and its precision is high.

Ball screw； Contact angle； Precision； Finite element analysis

10.19335/j.cnki.2095-6649.2016.09.009

CHEN Wan， WANG Ke-she， SONG Jie， et al. Analysis and Verification of the Best Contact Angle in Ball Screw［J］. The Journal of New Industrialization， 2016， 6（9）： 53-57.

陈婉，王科社，宋杰，等.高精度滚珠丝杠最佳接触角的分析与验证［J］. 新型工业化，2016，6（9）：53-57.

北京市科技计划课题121100001612010

陈婉（1991-），女，硕士研究生，主要从事滚珠丝杠性能研究；

王科社（1958-），男，硕士生导师，研究方向为机械设计、可靠性理论。