膨化机快开门盖的动态特性研究

马 力孙国友 方书起,2 白 净,2

(1. 郑州大学化工与能源学院，河南 郑州 450001；2. 生物质炼制技术与装备河南省工程实验室，河南 郑州 450001)



膨化机快开门盖的动态特性研究

马 力1孙国友1方书起1,2白 净1,2

(1. 郑州大学化工与能源学院，河南 郑州 450001；2. 生物质炼制技术与装备河南省工程实验室，河南 郑州 450001)

在自行设计的新型玉米籽粒膨化机的基础上，利用Fluent软件提供的动网格计算方法和物理模型，考虑膨化机内部气体的高温高压特性，对膨化机快开门盖的运动过程进行动态数值模拟。通过动网格的生成与消亡，较好地解决因门盖运动所导致的计算区域瞬时变化问题。得到膨化机在不同内部压力、筒体大小及接管管径下，门盖所受压力、能达到的最大速度等特性的可视化仿真结果。结果表明：膨化机门盖运动的最大速度随着膨化机内部压力和膨化机筒体体积的增加而增大，其所具有的能量随着接管管径的增大而增加。

膨化机；动网格；高温高压；门盖

随着生活水平的不断提高，人们对爆米花等休闲食品[1-3]的需求量迅速增加。虽然目前市场上存在多种样式的爆米花机，但都存在着原料品种单一、生产效率低下等缺点。为此，在老式爆米花机的基础上设计了一种新型的玉米籽粒膨化机，该膨化机可对各种谷物原料进行加工制作，并且可大大提高单位时间生产量。

在新型膨化机的工作过程中，带压开启阀门是一个必要的步骤。带压开启使得膨化机内部的气体急速膨胀，压力迅速减小，玉米籽粒内外压强差变大，导致籽粒内高压水蒸气急速膨胀，瞬时爆开米粒，即形成爆米花[4-6]。而膨化机正常工作压力可达到5～6倍的大气压，并且内部气体温度可达到250 ℃左右，带压开启对阀门的结构有较高的要求，因此，对膨化机阀门盖在高压下的开启过程进行研究可以为阀门盖的设计提供一定的依据[7-8]。

膨化机门盖的动力响应过程本质上是一种流固耦合问题，门盖在内部高压气体的作用下脱离原有的位置进行运动[9-11]。应用Fluent动网格技术，对膨化机阀门盖带压开启之后的运动状态进行了数值模拟[12-13]，比较了在不同的初始条件下阀门盖所能达到的最大速度，并进行了规律性的总结，为阀门盖的结构设计提供了一定的理论依据[14-17]。

1 数值模拟

1.1 几何模型的建立

在新型玉米籽粒膨化机的设计中，采用的是老式爆米花机的快开阀门的结构型式。图1为数值模拟所建立的膨化机简化模型。在对膨化机门盖的带压开启过程进行模拟时，认为阀门盖只在内部高温高压气体的冲击作用下进行运动，因此，对于实际设备中对运动响应过程影响不大，但却极大地增加收敛难度的附件结构采取了忽略处理。

1.2 基本假设

本研究中膨化机门盖的数值模拟过程采用二维条件下的轴对称分析。如图1所示，简化后的物理模型不论从结构上还是从施加的载荷上来说都满足二维轴对称问题的分析条件。数值模拟中采用的主要假设如下：

① 认为膨化机内部的介质为高温高压空气，温度设置为550 K，外部大气环境温度设置为300 K，压力为101 kPa；

② 内部气压在初始状态时保持稳定；

③ 忽略重力对门盖的作用；

④ 膨化机筒体与门盖的变形微小，均可忽略不计，认为这两者都为刚体。

1. 筒体 2. 接管 3. 法兰 4. 阀门盖

1.3 控制方程

为了真实地模拟计算膨化机门盖运动过程中的特性，在流体软件Fluent的基础上，利用用户自定义函数UDF实现动网格技术，采用二维轴对称模型对膨化机门盖的运动过程进行了非定常数值模拟，获得了门盖在运动过程中整个计算域的流场状态及门盖的运动特性。以下是本研究数值模拟中所使用的控制方程：

(1) 连续性方程：

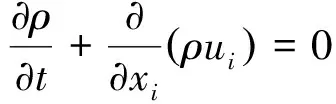
(1)

式中：

ρ——流体密度，kg/m3；

t——时间，s；

u——速度张量，m/s；

i——坐标轴方向，i=1,2,3分别为x，y，z坐标轴方向。

(2) 能量方程：Fluent中的能量方程的形式为

(2)

式中：

keff——有效热导率，W/(m·k)；

Sh——源项，W/m3。

式(2)等号右边的前三项分别表示由于导热、组分扩散和粘性耗散所产生的能量传递。

(3) 湍流方程：湍流方程采用标准k-ε模型，是一种两方程形式的湍流模型。这种模型把湍流的粘性与湍流动能(k)和耗散率(ε)相联系，建立起他们与涡粘性的关系，这种模型在工程上被广泛采纳。因此应用标准k-ε方程，其方程如下：

湍动动能方程

(3)

湍动能耗散率ε方程

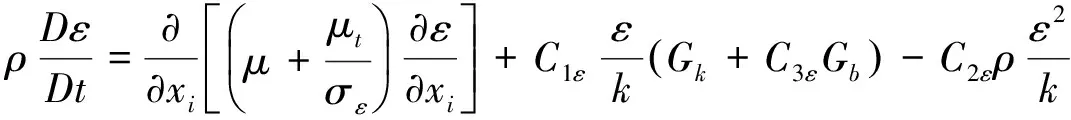
(4)

式中：

μl——层流的粘性系数，m2/s；

μt——湍流的粘性系数，m2/s；

Gk——由于层流速度梯度的存在而产生的湍流动能，J；

Gb——由浮力产生的湍流动能，J；

C1ε、C2ε、C3ε、σk和σε——经验常数。

(4) 气体的状态方程：在模拟中应用了理想状态下的气体方程，如下所示

(5)

式中：

pop——实际操作压力，Pa；

p——标准的大气压，Pa；

Mw——气体的摩尔质量，kg/mol。

1.4 边界条件

由于膨化机筒体、接管和门盖处的固体变形均可忽略不计，故用来限定流体区域，定义壁面边界2；由于本模型形状及其所受载荷具有轴对称几何体的特性，所以定义边界1为对称轴；对膨化机门盖失去约束后运动的瞬态过程来说，高压气体存在一定的回流流动，所以外流场边界条件使用压力出口边界3，压力设置为标准大气压力(101 kPa)，与实际情况是相符的。在初始状态下，膨化机内外所受压力不同，因此应对流场内外两个区域分别赋予不同的初始压力。

2 模拟结果与分析

2.1 膨化机门盖运动过程分析

在有机化学中就讲述过羧酸可以被还原，但脂肪酸在高温及催化剂存在下往往被氢化还原为醇，所以此类还原反应被称为氢解（或氢化反应）。

首先以膨化机内部压力设置为0.5 MPa、膨化机体积0.08 m3、接管大小为φ150×4.5 mm为初始模型，对膨化机门盖的运动过程进行模拟分析。图3、4分别表示在膨化机门盖飞出之后，其所受压力和速度随时间的变化图线。由图3、4可知，当膨化机门盖开始运动，其所受压力在0.04 s的时间内迅速降低，同时门盖的速度有一个快速增加的过程；当门盖运动0.04 s后，其所受压力基本上趋于平衡，此时门盖的速度也达到最大值；之后，由于模拟过程中忽略了重力作用，门盖会在前后压差的作用下速度略有减小，依靠惯性一直运动下去。

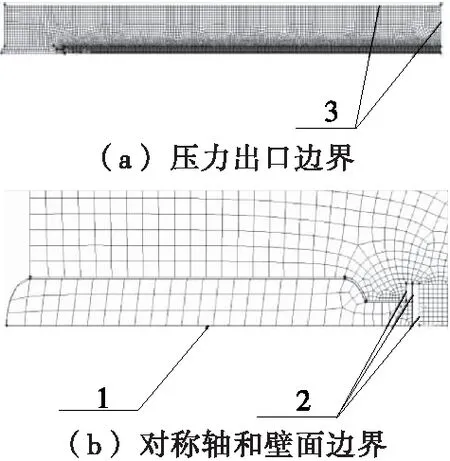
图2 (a/b)边界条件示意图

由图5可知，在膨化机门盖接触约束开始运动时，会受到膨化机内部压缩空气的强烈冲击，膨化机内部压力迅速降低，而门盖在此冲击作用下，会有明显的加速过程，这和图4中门盖的速度曲线相吻合；达到最大速度后，门盖运动方向上的压力大于背面的压力，并且两面压力差较小，门盖就会以一种缓慢的减速过程一直运动下去。

本研究对所用模型主要从膨化机内部压力、膨化机筒体体积和接管管径大小三方面对门盖的运动响应进行了研究。根据模拟结果显示，在上述3种因素影响下，膨化机门盖的受力曲线和速度曲线的走向基本一致，不同的是门盖所能达到的最大速度以及达到最大速度时的位移，因此，本研究以最大速度和位移为研究目标，对3种因素下膨化机门盖的运动响应进行了规律性的分析。

2.2 膨化机内部压力对门盖的影响

表1为在不同的膨化机内部压力下，门盖所能达到的最大速度以及达到最大速度时门盖的位移情况。

由表1可知，随着膨化机内部压力的增大，门盖所能达到的最大速度随之增加，达到最大速度时门盖的位移也有所增加，而达到最大速度时门盖运动所经历的时间却略有减小。结合上述门盖运动过程中的流场变化情况可知，主要是因为在较大压力下开始膨化时，门盖飞出速度较快，导致膨化机内部的压缩气体向外扩散的通道变大，作用在门盖上的压力减小，使得膨化机门盖在较短时间内就达到平衡状态，也即达到最大速度。为了精确地表示快开门盖所能达到的最大速度(vm)和筒体内部压力(p)之间的关系，运用Origin软件对两者之间的数据关系进行拟合，得到两者之间的关系图线为：

vm=39.63p-1.95(R2=0.999)。

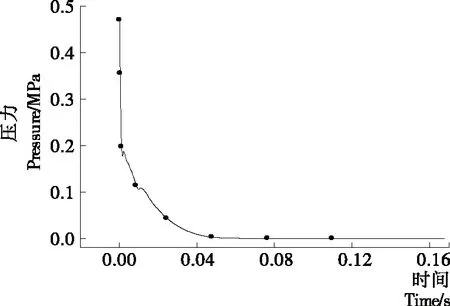
图3 快开门盖压力随时间变化曲线

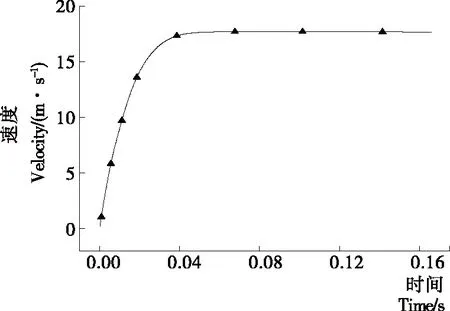
图4 快开门盖速度随时间变化曲线

图5 不同运动时刻压力云图

压力/MPa时间/s位移/m速度/(m·s-1)0．50．1161．30922．70．60．1112．12927．80．70．1052．37533．90．80．1002．57338．80．90．0972．81843．5

(6)

由式(6)可知，最大速度和筒体内部压力之间呈现一种正相关关系。

2.3 膨化机体积对门盖运动的影响

表2为在不同的膨化机筒体体积下，门盖达到的最大速度与所经历的时间和位移的关系。其中，5种膨化机筒体体积是在保持一定径高比的前提下进行放大的。

由表2可知，门盖所能达到的最大速度以及达到最大速度所经历的时间和位移均随着膨化机筒体体积的增加而增大。需要指出的是，虽然上述5种模型中膨化机的体积增加，但并没有改变接管的管径大小，也就是说膨化机筒体的内径和接管管径的比值在不断扩大，这就导致门盖在运动过程中受到的膨化机内部压缩气体的冲击作用时间在不断增加，使得门盖在较远距离处才达到平衡状态，即达到最大速度。同样拟合出最大速度和筒体体积(V)之间的数量关系式：

表2 不同体积下快开门盖的运动响应

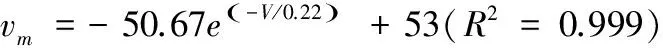
(7)

其曲线形式见图6。

图6 最大速度和筒体体积之间的关系图线

由图6可知，最大速度的走势随着体积的增大而逐渐变缓，这说明当体积增加到一定值时，在给定的内部压力和管径下，筒体体积对最大速度的影响有所减小。

2.4 接管管径对门盖运动的影响

表3为不同接管管径对门盖所能达到的最大速度以及达到最大速度所经历的时间和位移的影响。其中膨化机筒体体积选取0.37 m3，内部压力设置为0.5 MPa。

由表3可知，随着接管管径的增大，门盖达到最大速度所经历的时间和位移均呈现减小趋势，这是由于管径增大导致膨化机内部气体扩散通道扩大，其对门盖的冲击作用时间减少，位移也随之减小。但在门盖所能达到的最大速度减小的同时，门盖的质量却随着接管管径的增大而增加，所以为了更好地比较管径对门盖运动的影响，将以门盖达到最大速度时所具有的动能为目标，见图7。

表3 不同接管管径下快开门盖的运动响应

由图7可知，随着接管管径的增大，门盖运动过程中所具有的能量也随之增加，基本上呈现出一种正比例关系。

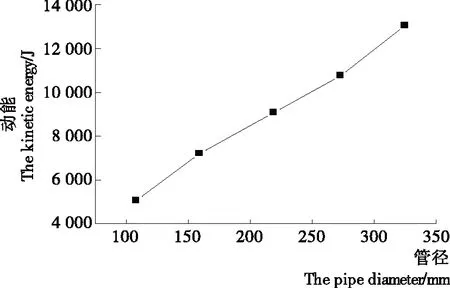
图7 门盖能量的变化图线

3 结论

本研究建立了膨化机门盖的物理模型和仿真模型，利用Fluent软件的动网格技术实现了运动流场的数值模拟，并对模拟结果进行了分析。由分析可知：

(1) 当膨化机门盖开始运动，其所受压力在很短的时间内迅速降低，同时门盖的速度有一个快速增加的过程；当门盖运动一段时间后，其所受压力基本上趋于平衡，此时门盖的速度也达到最大值；最终依靠惯性继续飞行。

(2) 在不同的筒体内部压力作用下，膨化机门盖的运动过程基本相同，但其所能达到的最大速度随着膨化机内部压力的增加而增大。

(3) 由于接管管径大小的限制，随着膨化机体积的增加，其对门盖的作用时间延长，造成门盖达到最大速度时其运动时间和位移均呈增加趋势。

(4) 在一定的膨化机体积和内部压力下，随着接管管径的增大，膨化机内部压缩气体扩散的通道不断扩张，使得气体作用于门盖的时间缩短，位移减小，但门盖达到最大速度时所具有的能量却在不断增加。

本研究并没有考虑重力对门盖运动的影响，并且是在二维的情况下进行研究和分析的，虽然有利于对问题的简化，但与实际情况之间存在一定的差距，因此以后的研究可以考虑在三维且考虑重力因素情况下来分析膨化机门盖的实际运动过程。

[1] 蒲彪, 王庆忠. 我国方便食品的市场前景[J]. 食品与机械, 2002(3): 35-37.

[2] 黄儒强, 苪汉明, 陶学红, 等. 爆裂玉米的微波膨化特性研究[J]. 食品与机械, 2001(1): 20-21.[3] 郑刚, 李冀新, 刘娅, 等. 影响挤压小吃食品品质的因素[J]. 食品与机械, 1999(4): 28-29.

[4] 许德昌, 袁胜发. 气动式爆米花机的研究[J]. 液压与气动, 2011(2): 7-8.

[5] 刘越. 蒸汽爆破预处理技术对污泥厌氧消化影响的研究[D]. 四川: 农业部沼气能源研究所, 2014: 10-11.

[6] 刘苗苗, 张正茂, 卓武燕, 等. 不同种类小麦爆米花特性比较研究[J]. 西北农业学报, 2015, 25(5): 48-55.

[7] 龚曙光, 谢桂兰花, 王亚, 等. 基于有限元分析的快开门装置结构优化设计[J]. 机械设计与研究, 2004, 20(1): 83-85.

[8] 韩树新, 盛水平, 刘延雷, 等. 快开门式压力容器余压开门爆炸数值仿真研究[J]. 中国安全生产科学技术, 2010, 27(2): 50-54.

[9] 孙帮成, 李明高. ANSYS Fluent14.0仿真分析与优化设计[M]. 北京: 机械工业出版社, 2013: 35-40.

[10] 葛如海, 王桃英, 许栋, 等. 基于动网格和UDF技术的气缸动态特性研究[J]. 机床与液压, 2010, 38(21): 12-15.

[11] 刘骁. 快开门式压力容器带压开启过程数值模拟研究及结构安全性改进分析[D]. 浙江: 浙江大学, 2014: 31-48.

[12] 蔡子金, 李军庆, 张庆文, 等. CFD在搅拌罐性能研究和生化过程放大中的应用[J]. 食品与机械, 2013, 29(6): 108-12.

[13] 杜飞龙, 李少波, 何玲. 卧式组合搅拌槽内固液混合物多相流模拟分析[J]. 食品与机械, 2013, 29(5): 111-114.

[14] 伍贻兆, 田书玲, 夏健. 基于非结构动网格的非定常流数值模拟方法[J]. 航空学报, 2011, 32(1): 15-26.

[15] 郭崇志, 姚远. 安全阀超压泄放过程动力学参数分析与测试[J]. 化工进展, 2015, 34(3): 628-637.

[16] 朱建安, 彭飞, 郭培红, 等. 煤仓清堵空气炮瞬态冲击试验研究[J]. 矿山机械, 2012, 40(6): 107-109.

[17] 幸莎. 安全阀开启流场参数的模拟与试验研究[D]. 广东: 华南理工大学, 2013: 25-46.

Dynamic characteristics of quick actuating valve of expangding machine

MA Li1SUNGuo-you1FANGShu-qi1,2BAIJing1,2

(1.SchoolofChemicalEngineeringandEnergy,ZhengzhouUniversity,Zhengzhou,Henan450001,China;2.EngineeringLaboratoryofHenanProvinceforBiorefineryTechnologyandEquipment,Zhengzhou,Henan450001,China)

expanding machine; dynamic mesh; high temperature and pressure; the valve; the movement

国家自然科学基金项目(编号：21176227)

马力，男，郑州大学在读硕士研究生。

方书起(1964—)，男，郑州大学教授。

E-mail：fangsq@zzu.edu.cn

2016-02-08

Abstracct: The movement of the quick actuating valve of expanding machine was simulated by using the calculation and physical models of Fluent software, considering the condition of the gas with high temperature and pressure, and this was newly self-designed for the corn grain. The problem of regional instaneous change in calculation area resulted by valve moving was well solved with generation and disappearance of dynamic mesh. The visualization simulation results of the pressure on the valve and the maximum velocity of the valve, produced at different internal pressure, volume, and the pipe diameter were. The results showed that the maximum velocity of the quick actuating valve of expanding machine increaseed with the internal pressure and the volume of the expanding machine, and the energy of the valve increases with the pipe diameter.