高师院校本科生MPCK发展的调查研究*

陈　蓓

(1.江苏第二师范学院　教务处，江苏　南京　210013；2.南京师范大学　课程与教学研究所，江苏　南京　210097)



高师院校本科生MPCK发展的调查研究*

陈蓓1，2

(1.江苏第二师范学院教务处，江苏南京210013；2.南京师范大学课程与教学研究所，江苏南京210097)

在数学学科教学知识(MPCK)理论的基础上，利用高师院校本科生MPCK 发展研究调查问卷，对531名数学专业师范生进行测试，结果表明：样本师范生的MPCK发展水平一般，并存在显著差异；学校、年级是影响师范生MPCK发展的主要因素；MK、PK、CK对MPCK的影响效果不一，且两两变量之间的直接相关非常显著。基于调查研究，提出发展师范生MPCK的基础、核心和路径：模块化、动态式的课程设置，全程化、行动式的实践教学，嵌入化、渐进式的知识结构。

师范生；MPCK；发展

一、引言

自美国学者Shulman[1]在20世纪80年代首次提出学科教学知识(Pedagogical Content Knowledge，简称PCK)以来，教师专业知识的研究迅速成为众多研究者聚焦的课题，教师知识对教师信念、教学行为、教学效果的影响也日益受到关注。就数学教师而言，数学学科教学知识(Mathematics Pedagogical Content Knowledge，简称MPCK)的储备，直接决定着数学教学的有效性。目前，国内外对MPCK的研究主要集中在它的内涵、构成、特征、价值、发展途径等方面[2-8]。大家一致认为，数学教师拥有的MK(Mathematics Knowledge)、PK(Pedagogical Knowledge)、CK(Content Knowledge)越多，其交集MPCK的内涵就越丰富，就越容易对数学进行“加工”，将“知识形态”的数学转化为“教学形态”的数学，转化为学生容易“消化”的知识。

一方面，正是在这样的研究背景下，更多的学者开始关注高师院校本科生MPCK发展现状[9-10]，关注数学教学相关知识结构的生成；另一方面，正在开展的高中数学课程标准修订工作提出数学核心素养及其内涵、学科价值、教育价值、表现层次等，强调合作交流、批判性思维和问题解决能力的培养。这些都对教师提出新的要求。对师范生而言，更应该从数学教学知识的角度，去完善教学所需要的、有用的、有效的知识。

因此，本研究探讨高师院校本科生MPCK发展现状，关注以下问题：(1)师范生MPCK的总体情况如何？(2)影响师范生MPCK发展的因素有哪些？(3)师范生MPCK不同维度对MPCK是否有显著预测作用？(4)探究师范生MPCK不同维度与MPCK之间的因果关系模型。通过对师范生MPCK发展现状的研究，反思其对数学教学质量的影响，也对高师院校数学教育专业课程的设置和教学改革提供借鉴。

二、调查过程与方法

(一)调查对象

本研究采用随机抽样的方法，从两所师范院校的数学教育专业本科生中抽取540名学生(大二至大四年级)作为被试，共发放问卷540份，有效问卷531份，有效率98%。因大一学生尚处于基础课学习阶段，故未选取其作为调查对象；抽取的大四学生已完成所有课程的学习和实习，正在撰写毕业论文。调查对象的基本情况详见表1。

表1　样本人数(有效问卷数)

(二)调查工具

在仔细研读文献的基础上，就相关问题与专家进行深入讨论，编制了数学专业师范生 MPCK 发展研究的调查问卷，问卷由三部分组成。

第一部分是数学专业师范生的基本信息，包括性别、年级、生源、职业定位和对待实习的态度。

第二部分是问卷主体部分，包括教师MPCK的四个维度：MK、PK、CK和TK[3]10-14。其中，MK维度6个题项，PK维度16个题项，CK维度11个题项，TK维度4个题项，共37个题项。每个项目均使用利克特(Likert)5点记分法，1表示“非常不赞同”，2表示“不太赞同”，3表示“不能判定”，4表示“基本赞同”，5表示“完全赞同”。分别赋值1、2、3、4、5分，反向题目分别赋值5、4、3、2、1分。

第三部分主要考查师范生对课程设置的满意程度以及对实习、师范生专业知识和能力培养等方面的期望和要求。

问卷回收整理后，用SPSS 19.0进行数据分析。

(三)问卷信效度分析

1.信度分析

数学专业师范生 MPCK 发展研究调查问卷的信度分析结果见表2，师范生MPCK各维度内部一致性系数在0.700～0.838之间，总问卷内部一致性系数为0.861。可见，该调查问卷的α信度指标达到测量学要求，适宜作为测量工具使用。

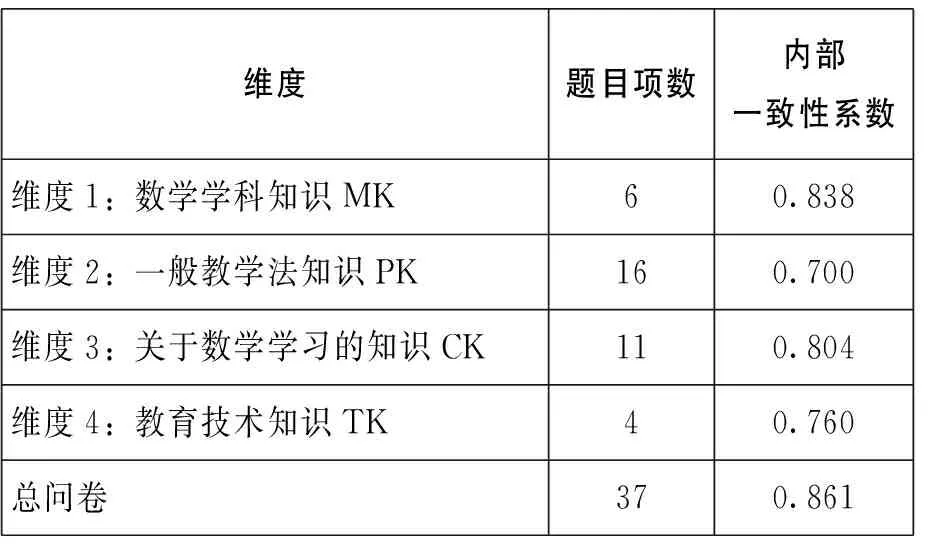
表2　问卷信度分析结果(Cronbach's Alpha系数)

2.效度分析

考察问卷各维度之间的相关性，结果如表3所示，四个维度MK、PK、CK、TK与总问卷MPCK之间的相关在0.284～0.787之间，均达到非常显著性相关水平，表明各维度与总体概念一致。各子维度之间的相关明显低于各子维度与总问卷的相关，表明各子维度有相对独立性而且都与总问卷有高依存关系，问卷有较好的结构效度。

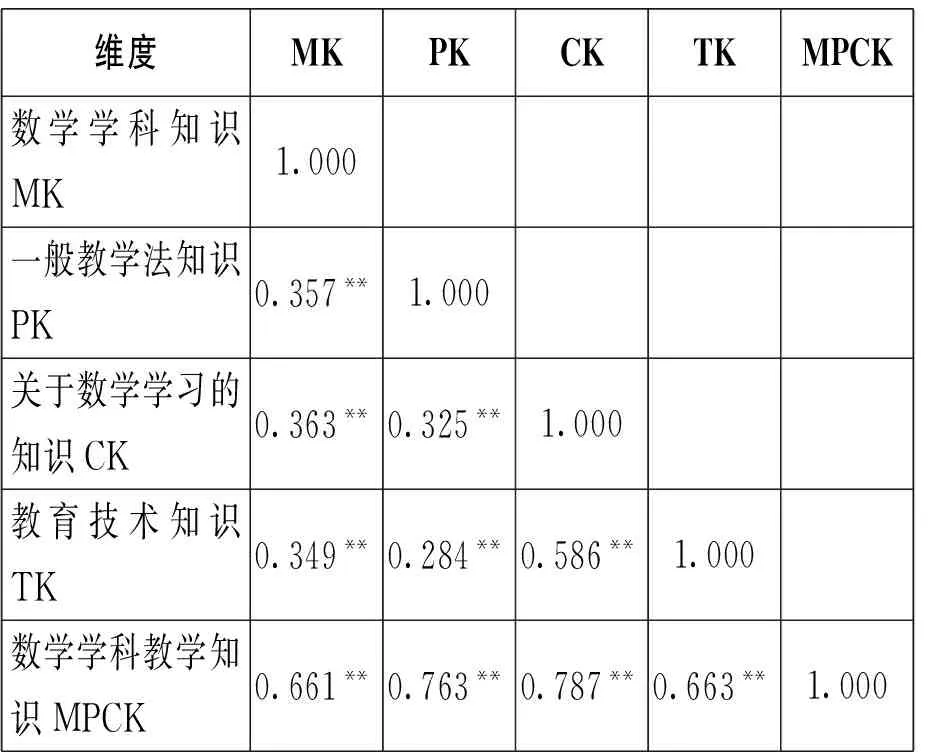
表3　问卷各维度及总问卷的相关矩阵(r)

注：**表示在0.01 水平(双侧)上显著相关，同图1。

三、调查结果及分析

(一)师范生MPCK的总体情况分析

通过对高师院校师范生MPCK测试数据进行频数分析，得到问卷总分的频数分布表，详见表4。

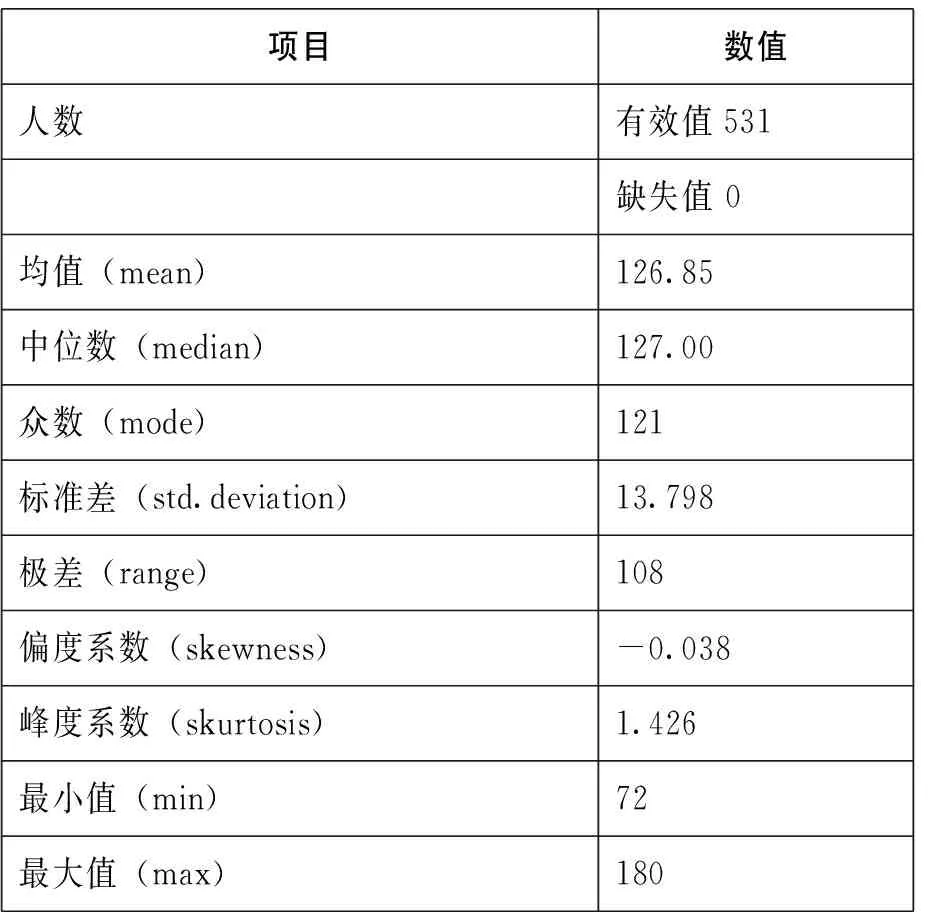
表4　问卷总分的频数分布表

从统计结果可见，大多数师范生数学学科教学知识水平处于中上，且大致发展情况相近。进一步对师范生在MPCK四个维度的得分进行统计描述，结果见表5。

表5　师范生MPCK发展情况的整体性描述

表5反映了高师院校师范生MPCK发展的整体情况，得分情况由高到低依次为PK、CK、MK、TK，表明师范生数学学科教学知识由强到弱依次为：一般教学法知识、关于数学学习的知识、数学学科知识、教育技术知识。进一步对师范生MPCK四个维度的数据进行单因素方差分析，显著性sig=0.000，呈非常显著性差异。

(二)师范生MPCK的影响因素分析

1.学校

对不同学校师范生MPCK结果进行差异比较，采用t检验，得到表6。

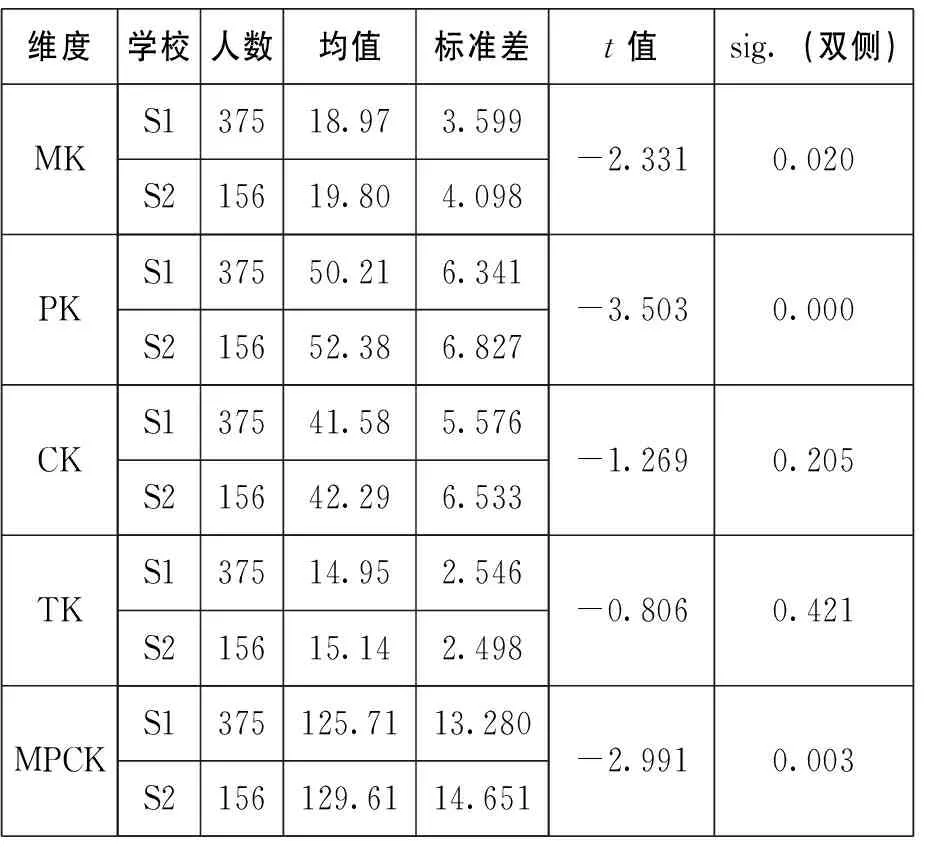
表6　不同学校师范生MPCK描述性统计量

结果发现不同学校师范生MPCK发展的差异显著(p<0.05)，从问卷各维度均值的分布情况可以看出：在问卷的各个维度，学校S2学生的平均分都略高于学校S1的学生。其中，在教学法知识方面，两所学校的学生差异最大；其次为数学学科知识，差异最小的是关于数学学习、教育技术的知识。所以，不同学校师范生MPCK发展的差异主要表现在数学学科知识、教学法知识，尤其是在教学法知识的认识方面，两所学校学生的差异最大。

2.性别

采用独立样本t检验，分析不同性别师范生MPCK是否存在性别差异，得到表7。

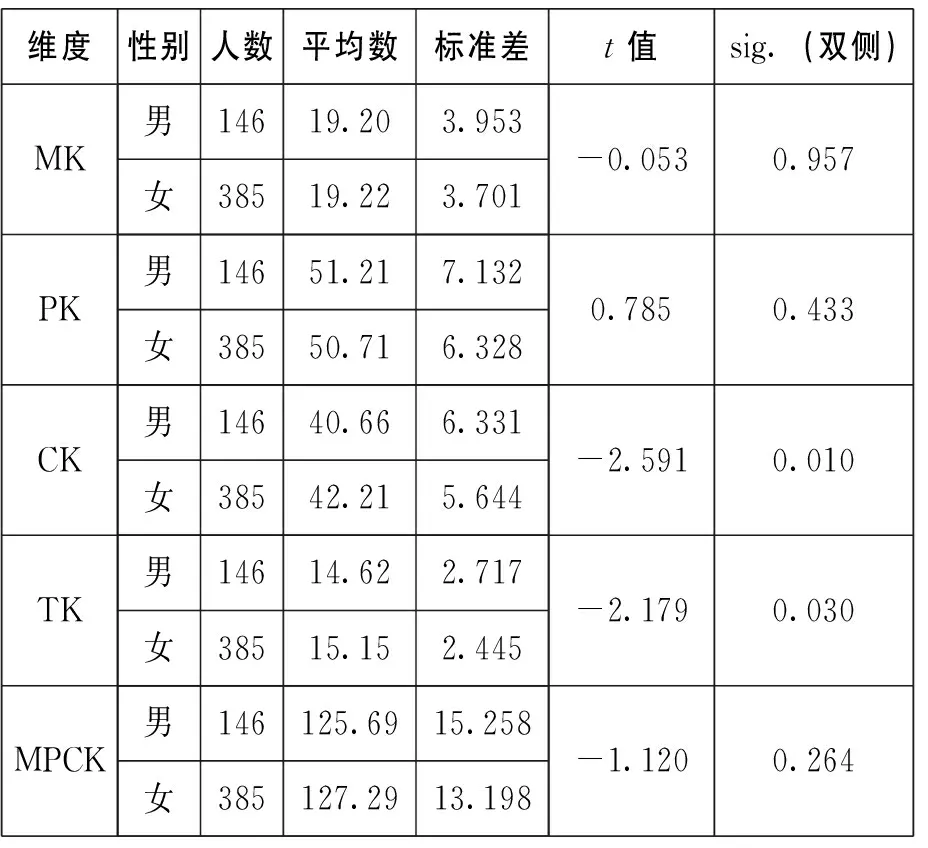
表7　中学数学教师认识信念系统的性别差异比较

如表7所示，男女师范生在MPCK发展方面得分统计没有显著性差异。在MPCK各个维度的性别差异比较上，男女生在关于数学学习的知识、教育技术的知识方面存在显著差异。

3.年级

采用单因素方差分析方法，检验师范生MPCK及其分维度上的得分是否存在年级差异，得到表8。

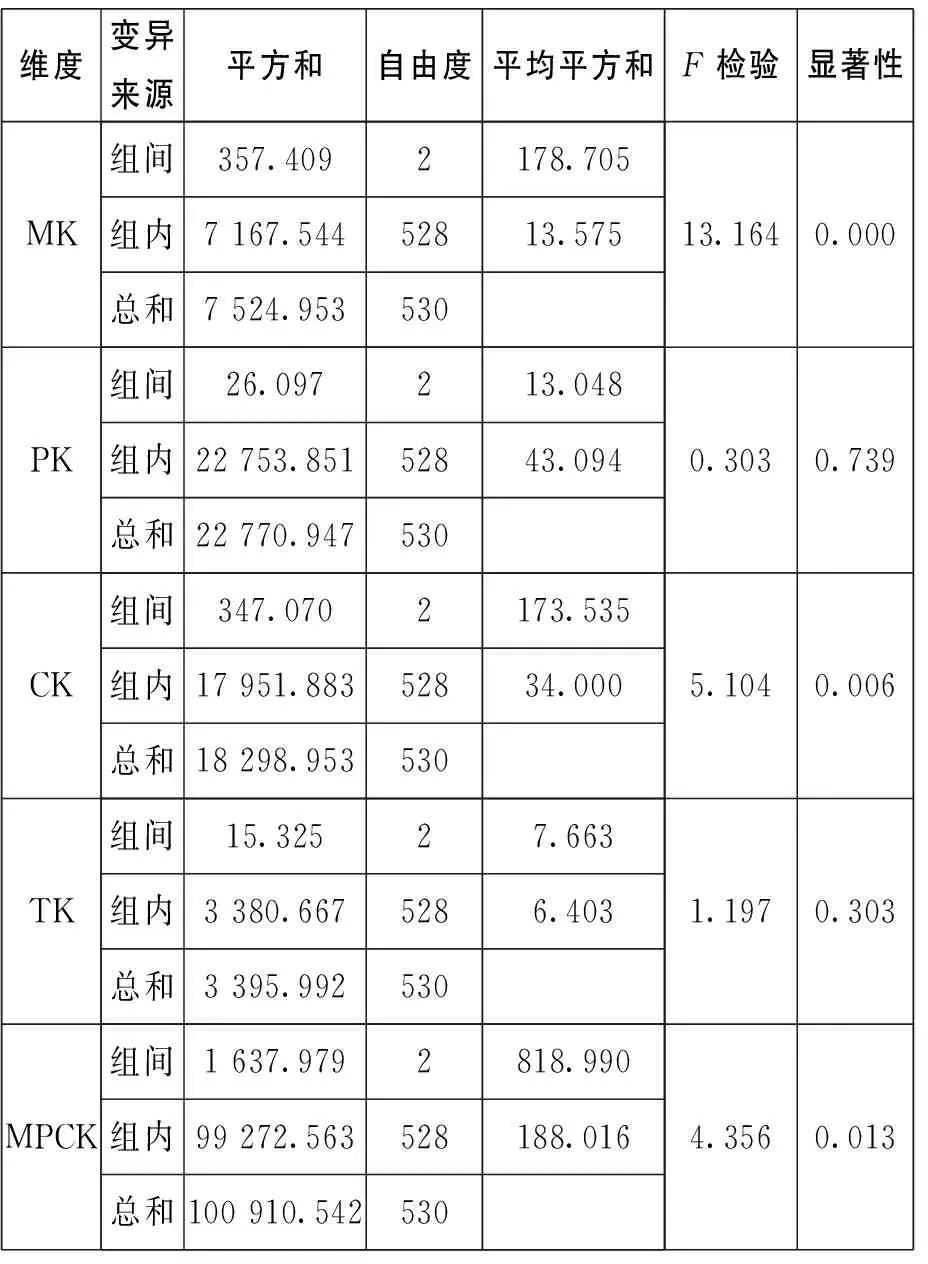
表8　不同年级师范生MPCK发展差异比较

不同年级师范生在MPCK总维度上(F(2，528)=3.328，P<0.05)存在显著差异，以及关于数学学科知识(F(2，528)=13.164，P<0.01)、关于数学学习的知识(F(2，528)=5.104，P<0.01)两个MPCK分维度层面存在非常显著差异。总体来看，不同年级师范生MPCK发展水平呈上升趋势，尤其在大四实习之后，有较大的发展。

(三)师范生MPCK发展的回归分析

通过回归分析，研究师范生MPCK发展的四个维度对其影响，将因变量MPCK定义为Y，MK、PK、CK、TK作为自变量依次定义为X1、X2、X3、X4，进行逐步回归分析，得到表9。

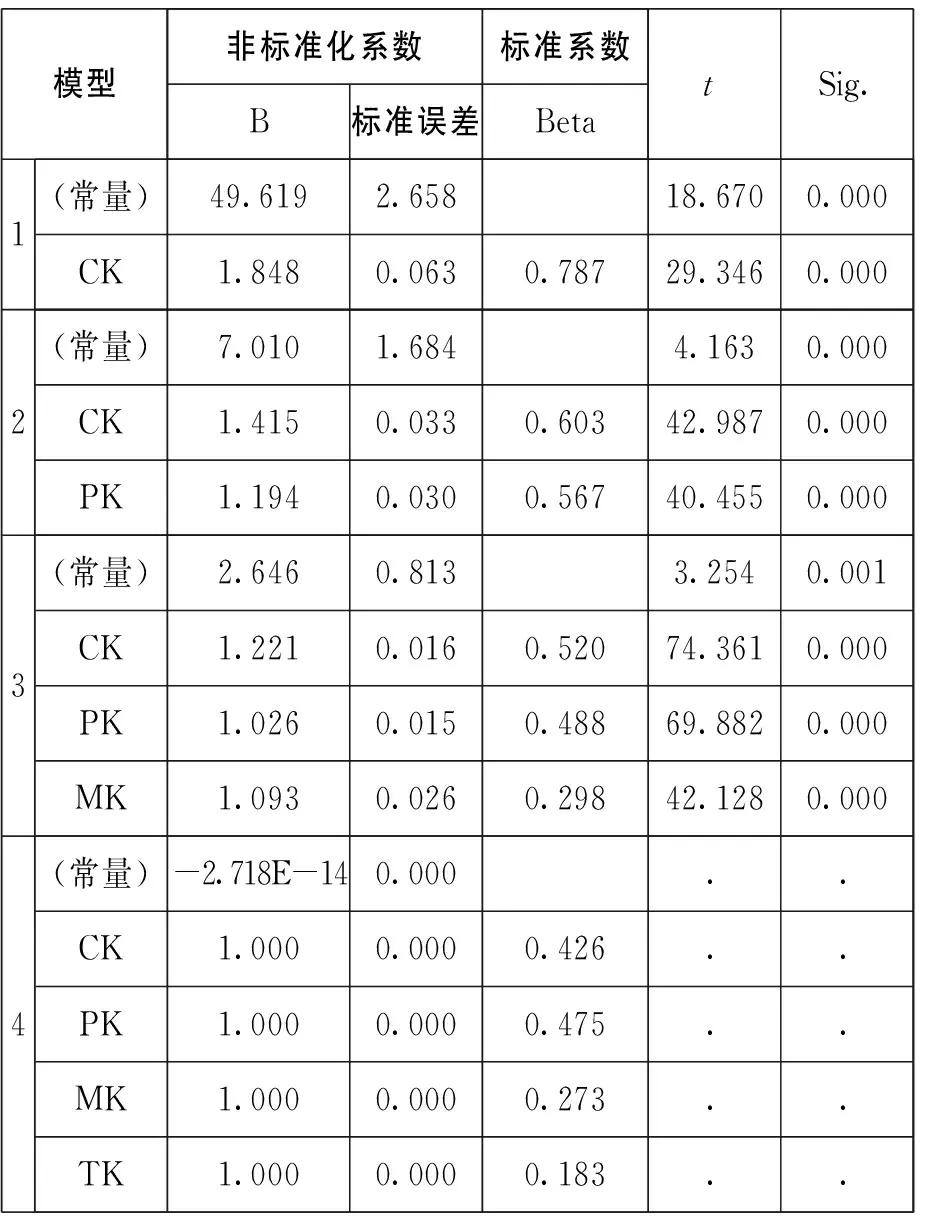
表9　师范生MPCK回归系数及其检验

(1)回归模型为：Y=1.848X3+49.619，显著性概率是0.000，表明回归极显著。(2)回归模型为：Y=1.415X3+1.194X2+7.010，显著性概率是0.000，表明回归极显著。(3)回归模型为：Y=1.221X3+1.026X2+1.093X1+2.646，显著性概率是0.000，表明回归极显著。(4)维度TK对MPCK的影响不显著，故不建立Y与X1、X2、X3、X4的回归方程。

(四)师范生MPCK发展的路径分析

在回归分析的基础上，进一步检验MK、PK、CK、MPCK之间的因果关系，探究变量与变量之间是否存在相关关系，影响的程度如何等。对四个变量进行路径分析，结果见图1。

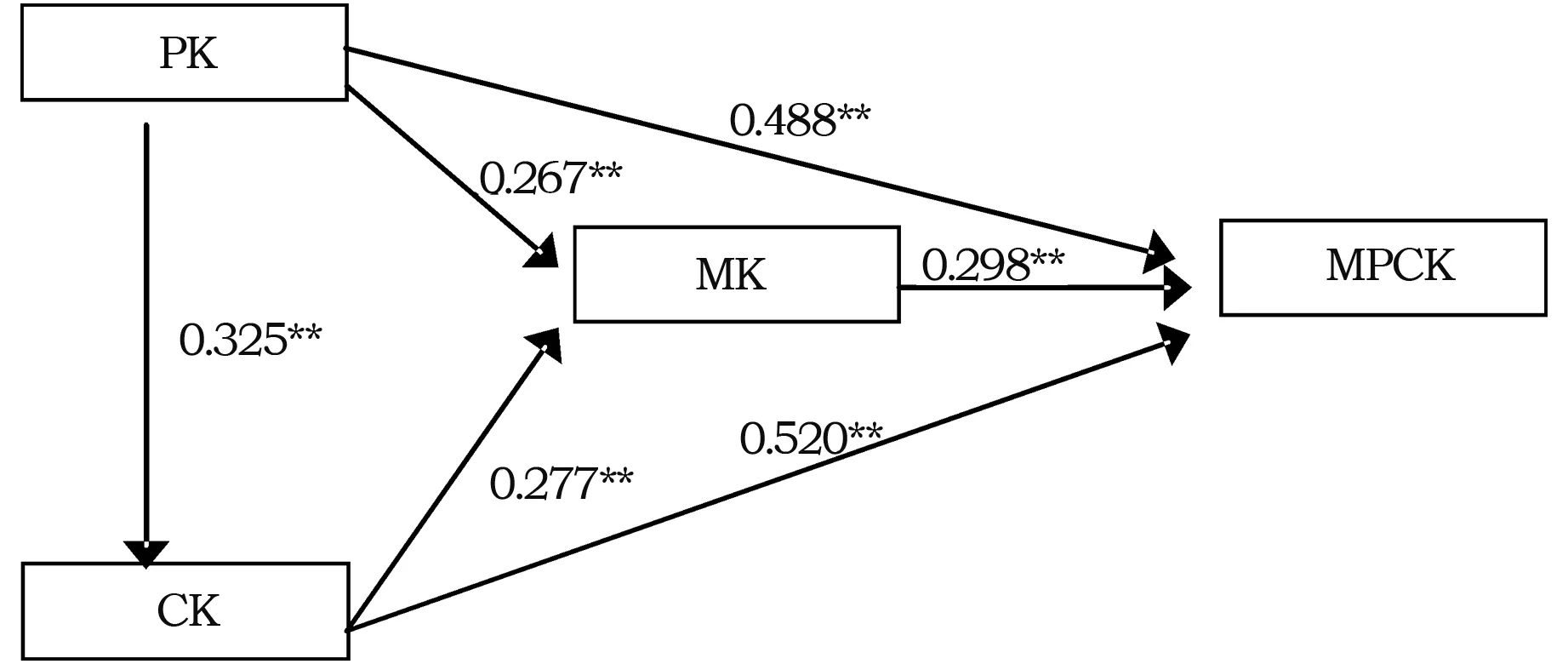
图1　MK、PK、CK与MPCK的路径图

从图1可以看到，CK对MPCK的直接影响效果是0.520，PK对MPCK的直接效果为0.488，MK对MPCK的直接影响效果是0.298，这三个效果都是比较大的，并且关于教学和学习的知识，对数学学科教学知识的影响更大。

PK对MPCK影响的间接效果：0.267×0.298+0.325×0.520+0.325×0.277×0.298=0.276。

CK对MPCK影响的间接效果：0.277×0.298=0.08。

MK对MPCK影响的可能效果：0.277×0.520=0.144。

因此，四个变量之间存在非常显著性的相关关系，并且以直接影响为主，通过中介变量间接影响或可能影响较小。

四、结论与讨论

(一)结论

(1)师范院校本科生MPCK发展水平一般，且在一般教学法知识、关于数学学习的知识、数学学科知识、教育技术知识方面差异性显著，不能进行MPCK各个维度知识之间较好的联结和贯通。(2)不同学校师范生MPCK发展水平差异显著，尤其表现在一般教学法知识、数学学科知识的理解两个维度，两所大学课程设置的不同，是学生MPCK差异的主要原因。(3)不同性别本科生MPCK发展水平差异不明显，男女生在关于数学学习的知识、教育技术知识方面差异显著。但总体而言，性别不是影响本科生MPCK的主要因素。(4)本科生MPCK发展水平具有显著年级差异，在大四尤其是实习之后有一个显著发展，具体表现在数学学科知识、数学学习知识两个方面有明显的增长。(5)CK、PK、MK对MPCK的影响显著，并且它们之间的关系可以用回归方程来进行预测和控制，师范生对数学教学、学生学习的理解是关键。(6)构建MK、PK、CK与MPCK的路径图，两两变量之间的直接相关非常显著，说明师范生必须具有良好的数学学习知识、教学法知识(含现代教育技术)、数学学科知识，才能产生高质量的数学学科教学能力，缺少某一要素都会直接影响优良MPCK的生长。

(二)讨论

1.模块化、动态式的课程设置是高师院校本科生MPCK发展的基础

通过实证研究，我们发现在课程设置方面主要存在以下问题：(1)数学专业课、教师教育类课程、数学教育类课程三者对本科生MPCK发展的意义何在？孰轻孰重？该如何均衡各类课程所占的比重？(2)大学高等数学知识的学习并没有加深师范生对中小学数学知识的理解，更不能在数学教学中发挥其作用。(3)本科生对数学课程标准、中小学数学教材不熟悉，数学学科知识缺乏。因此，课程设置作为本科生MPCK发展的基础，应根据师范生的需求做好顶层设计，建构模块化、动态式的课程模块。

首先，数学专业课(本学科+跨学科、必修+选修)模块，教师教育(理论+技能)模块，学科教学(理论+技能)模块三者应互为支撑，高等数学是中小学数学教师不可缺少的知识基础，教师教育、学科教学课程是将数学知识转化为教育形态知识的基础。与此同时，必修课应少而精、选修课应广而博，还要避免课程与课程的重复、不同课程相同教学内容的交叉，合理处理好各个模块中相应课程与教学内容、教师、学生的整合。

其次，在课程模块化的同时，强调课程的动态式设计，即理论+实践、系列+多样、专题+研究。所谓理论+实践，即推进课程教学方法的改革，将微课、MOOCs、Spoc、翻转课堂、案例、合作等实践教学方式融入课堂教学。所谓系列+多样，即推进课程的订单式服务，一门课程系列专题多位主讲教师，例如：增加数学课程标准解读与教材分析的课程单元，促进师范生对中小学数学知识的理解。所谓专题+研究，即推进课程的主题性、研究性，例如：通过课例分析，研究如何在高等数学的观点下，审视初等数学的知识结构，从而在教学设计中加以应用。

2.全程化、行动式的实践教学是高师院校本科生MPCK发展的核心

MPCK发展的核心是建构数学内容的教育形态，将本体性知识转化为实践性知识，而实现这个转化的有效途径即实践教学。从问卷第三部分调研结果中也发现，学生认为教育实习对今后的数学教学最有帮助，并希望延长教育实践的时间。所以，在课程教学中，贯穿全程化、行动式的实践教学，能有效促进高师数学师范生专业技能的形成和发展。

全程化实践教学，即从大一开始就让师范生进入真正的数学课堂，了解数学教学。例如：大一到大二每个学期赴中小学见习一周，大三每周赴中小学见习一天，大四实习一个学期，通过这样循序渐进的方式，处理好数学教育理论学习与数学教学实践训练的关系，在实践过程中促进师范生MPCK的养成。

行动式实践教学，即以行动研究为主要载体，通过实践教学，加深师范生对数学学科知识的理解，推进师范生专业技能的发展。例如：男生更加擅长信息技术和数学专业软件课程，女生对中小学生数学学习心理更加关注，可以通过合作学习，发挥男女生优势，取长补短，在实践中发展数学教学经验，实现数学、教学、学生知识的联合发展。

3.嵌入化、渐进式的知识结构是高师院校本科生MPCK发展的路径

师范生数学学科教学知识是嵌入、渐进的结构，也是一个协同发展的过程，正如MK、PK、CK与MPCK(图1)的单向作用路径图所示，MK、PK有直接联系，但不能独立于CK(TK)等知识。在嵌入化MPCK知识结构中，MK是核心，对数学知识理解得越深刻，就越能够把握数学知识的本质，并容易建立丰富的数学学科教学知识；MK也是载体，PK、CK只有附着于数学学科知识，才能够进行有效的MPCK整合。

与此同时，在MK基础上发展PK、CK，又反哺MK、MPCK的发展，这是一个循序渐进的过程，也是相互渗透、交叉的过程，更是促进MPCK有机整合的过程。所以，着眼于师范生MPCK发展的路径，不仅要关注MK、PK、MPCK之间的直接联系，还要注重联系的广度与深度，不断补充完善数学学科、教学、学习知识，通过数学学科知识和信息技术的有效整合，实现MPCK发展。

[1]SHULMAN L S.Knowledge and teaching：foundations of the new reform [J].Harvard Educational Review，1987，57(1)：1-22.

[2]童莉.数学教师专业发展的新视角：数学教学内容知识(MPCK)[J].数学教育学报，2010，19(2)：23-26.

[3]李渺，宁连华.数学教学内容知识(MPCK)的构成成分表现形式及其意义[J].数学教育学报，2011，20(2)：10-14.

[4]黄毅英，许世红.数学教学内容知识：结构特征与研发举例[J].数学教育学报，2009，18(1)：5-6.

[5]李渺，喻平，唐剑岚，等.高中数学教师知识结构的特征研究[J].数学教育学报，2007，16(2)：55-59.

[6]李琼，倪玉菁.教师知识研究的国际动向：以数学学科为例[J].外国中小学教育，2006(9)：6-11.

[7]汤炳兴，黄兴丰，龚玲梅，等.高中数学教师学科知识的调查研究：以函数为例[J].数学教育学报，2009，18(5)：46-49.

[8]刘俊华，胡典顺，纪静萍，等.高中数学教师MPCK发展的调查研究[J].数学教育学报，2015，24(1)：45-50.

[9]童莉.高师院校本科生数学教学内容知识的调查与分析[J].重庆师范大学学报(自然科学版)，2011，28(3)：85-88.

[10]章勤琼，郑鹏，谭莉.师范生数学教学知识的实证研究：以温州大学为例[J].数学教育学报，2014，23(4)：26-30.

(责任编辑李世萍)

Investigation on the MPCK Development of Undergraduates in theNormal Universities and Colleges

CHENBei1,2

(1.Teaching Affairs Office，Jiangsu Second Normal University，Nanjing，210013，China；2.Institute of Curriculum and Teaching，Nanjing Normal University，Nanjing，210097，China)

Based on the mathematics pedagogical content knowledge(MPCK)theory，the author uses questionnaires to test the MPCK development of mathematics major students and 531 students participated in the test.The results show that：MPCK development of the normal university students' is in the middle level and there is a significant difference；the school and grade are the main factors that influence the students' MPCK development；the effect of MK，PK，CK on MPCK is different，and the direct correlation between every two variables is very significant.Based on the above investigation and research，the basis，core and path of developing normal students' MPCK are proposed：setting the modular and dynamic course，providing the full course and action type of practical teaching，and applying the embedded and progressive knowledge structure.Key words：the normal universities' students；MPCK；development

2016-01-27

全国教育规划中小学数学教育研究重大招标课题“义务教育数学课程整体设计”(项目编号：GOA107001)；2015年江苏省教育厅基于测试分析的跟进式改革重大研究项目“义务教育学科核心素养和关键能力研究”(项目编号：2015jyktzd-02)；2013年江苏省高等教育教改研究立项课题“MPCK视角下‘三化一式’数学教育课程体系的优化与教学改革研究”(项目编号：2013JSJG145)；江苏第二师范学院2013年教学改革研究课题“MPCK视角下数学教育课程的教学改革与实践”(项目编号：Jssyjg2013zd12).

陈蓓(1981-)女，江苏常州人，副研究员，博士研究生，主要从事数学课程与教学论研究.

G658.3

A