基于PFC3D的粗粒土三轴试验细观参数敏感性分析*

李 灿 邱红胜 张志华

(武汉理工大学交通学院 武汉 430063)



基于PFC3D的粗粒土三轴试验细观参数敏感性分析*

李 灿 邱红胜 张志华

(武汉理工大学交通学院 武汉 430063)

以PFC3D为工具，以室内三轴固结排水试验作为基础，以加权平均数颗粒生成法建模.选择孔隙度、配位数、kn/ks、颗粒粒径分布、剪切速率和摩擦系数等细观参数作为研究内容，以应力应变强度曲线为力学分析方法，以颗粒转动速度场为变形分析手段，将各细观参数对粗粒强度的敏感性进行排序，对粗粒土剪切破坏的影响程度进行总结分析.研究表明，各细观参数对粗粒土强度及变形都有一定的影响，其中kn/ks对粗粒土强度及变形影响最大，孔隙度和配位数的影响最小.

PFC3D；细观参数；颗粒转动速度场

0 引 言

目前，试验及测试技术都无法获取其细观力学参数，无法很好揭示粗粒土宏观力学特性的内在作用机制.PFC作为离散元方法的一种，是细观分析的主要手段之一[1]，近年来在岩土工程领域得到了初步运用[2].粗粒土作为国内外岩土工程中主要的应用材料，运用PFC研究其宏细观力学特性的重要性是显而易见的.在数值模拟研究中发现，细观参数值的调整和标定是拟合试验结果成功的关键步骤.因此，在对粗粒土进行颗粒流数值模拟过程中，得出各细观参数对粗粒土强度及破坏变形影响的敏感性排序具有重要意义.

国内外研究学者运用PFC对粗粒土细观参数的研究很多，黄彦华等[3]分析围压以及岩桥倾角对断续双裂隙红砂岩强度破坏特征的影响规律，揭示断续双裂隙红砂岩在不同围压作用下裂纹扩展的细观力学响应机制；丛宇等[4]结合大理岩室内加、卸荷试验确定适用于岩石类材料的细观参数；唐文帅[5]得出随着颗粒最大粒径的增大，粗砂应力应变曲线的类型没有发生变化，初始杨氏模量变化不明显，但是峰值强度却随之减小；陈亚东等[6]提出了在三维离散元中与砂土的孔隙率、内摩擦角及压缩模量等宏观力学参数相匹配的细观参数确定方法，并给出了细观结构参数与宏观力学参数的函数关系.耿丽等[7]得出结论摩擦系数对材料的弹性性质影响不大，只与峰值强度有关；Huang[8]研究了粘性颗粒材料细观参数和宏观参数之间的相似关系；Nardin等[9]根据自定义的颗粒流接触模型和接触参数，建立了细观参数与宏观力学特性的定性关系.

研究发现，在选取细观参数进行研究时，未对一系列重要的细观参数进行全面系统分析.因此，文中在模拟三轴试验的基础上，选取孔隙度、配位数、kn/ks、颗粒粒径分布、剪切速率和摩擦系数等6种细观参数作为研究对象，通过应力-应变曲线和颗粒转动速度场来研究它们对粗粒土宏观力学及变形特性的影响.

1 三轴颗粒流模型

室内试验所用材料取自水布垭大坝工程的施工料场.用筛分法和混合法测试粗粒土的颗粒级配，得到粗粒土不同粒径范围内颗粒的含量见表1.

在颗粒流模型中使用不同参数调节方法，可能得到相同的宏观力学反应——应力-应变曲线.在三轴模型试验中，要考虑的因素很多，如初始杨氏模量Ec，颗粒抗剪强度c，φ，颗粒刚度比kn/ks，颗粒最小半径Rmin，颗粒最大、最小半径比Rmax/Rmin，试样的密度ρ，初始接触点个数Nf,摩擦系数f等.按试验结果应力-应变曲线弹性阶段计算初始杨氏模量，根据摩尔应力圆得到颗粒的抗剪强度，根据试验试样确定材料的密度，根据加权平均数颗粒生成法选取颗粒最小半径及最大、最小半径比，得到细观参数值，见表2.

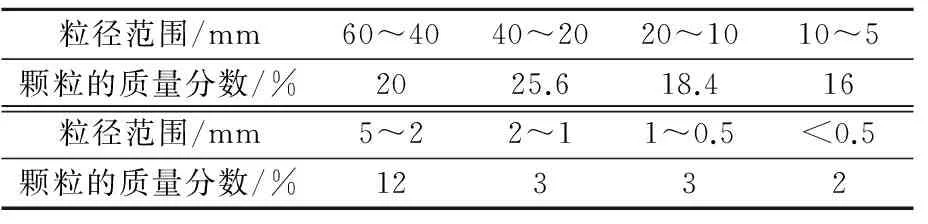
表1 粗粒土颗粒级配

表2 三轴数值模型中各细观参数

在PFC3D中合成材料土样是由球形颗粒组装而成的，模型是由一个圆柱形墙面围绕生成的颗粒体以及上下两面压缩板组成的.其中，上下2面压缩板在试样压缩过程中，上墙面对试样进行压缩剪切，下墙面保持不动；圆柱形墙面在压缩剪切过程中通过伺服系统维持恒定围压的工作.应力-应变数据的收集与整理是根据跟踪墙面所受力的情况，以及墙面相对位移决定的.对模型试样分6层进行标识颜色，其中，每层的厚度是100 mm；对圆柱试样从内到外分3层，每层厚度50 mm.模拟尺寸与室内三轴试验试样尺寸一致，为300 mm×600 mm(直径×高)，颗粒流三轴模型见图1.

图1 颗粒流三轴模型

2 数值结果与试验结果比较

根据已确定的细观参数，调整未知细观参数，得到围压为0.8,1.6,3.3 MPa下试样的应力-应变曲线，并将各数值结果与试验结果进行对比，见图2.

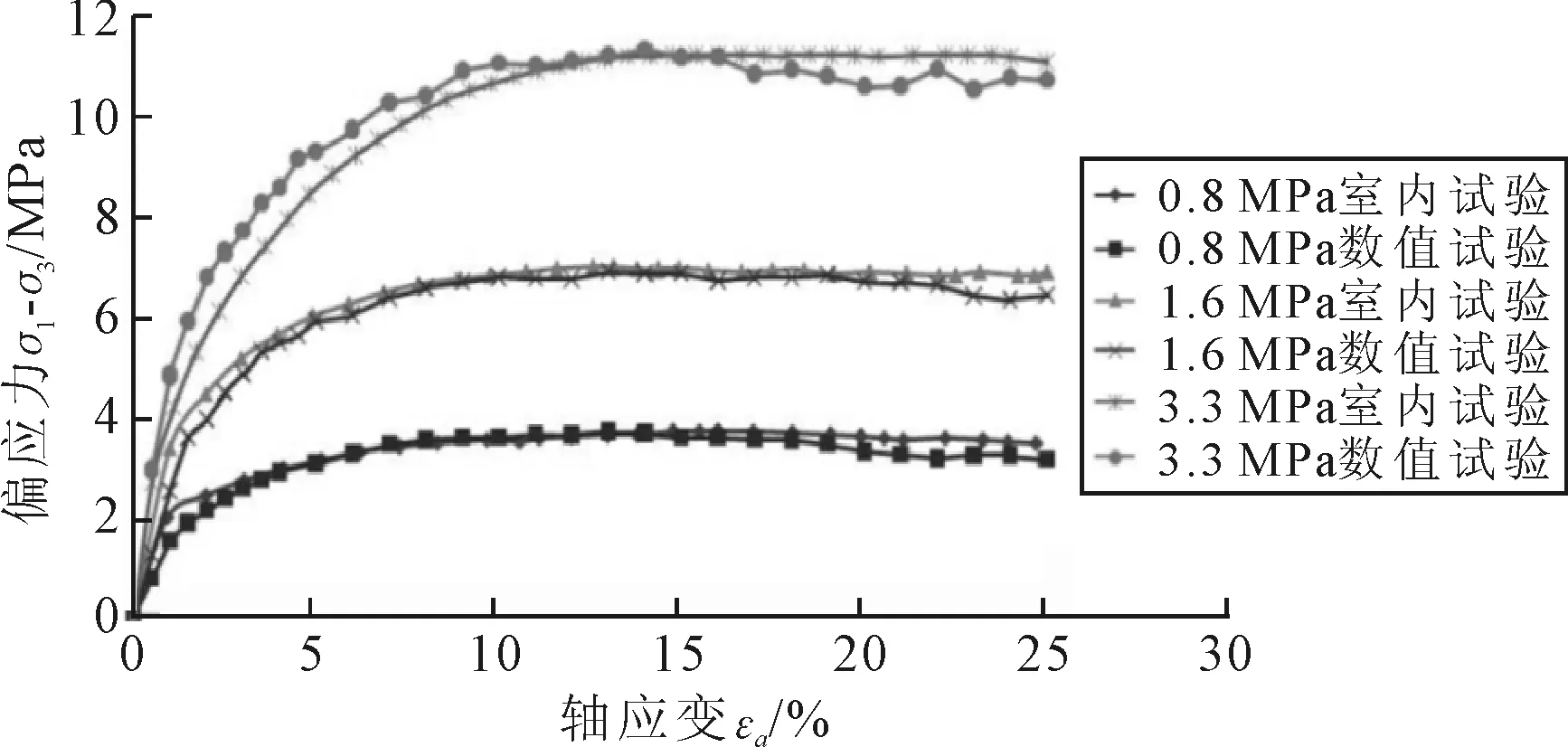
图2 不同围压下室内试验与数值试验应力-应变曲线

由图2可知，数值试验得到的应力-应变曲线与实验室里得到的应力-应变曲线基本吻合，数值模型中在竖向荷载作用下，首先随着轴应变的增大处于弹性阶段，该阶段处于轴应变小于10%；随着轴应变的继续增大，模型内部裂隙出现贯穿现象形成剪切面，此时模型处于塑性阶段.曲线在达到峰值强度时的轴应变也大体相同，试样达到临界状态之后也处于和室内试验一样的应变硬化现象，因此可用三维离散元数值试验模拟室内三轴试验.

3 细观参数敏感性分析

影响粗粒土强度及变形的因素很多，根据高等土力学中的土的抗剪强度与其影响因素的关系，可以确定为以下公式.

(1)

3.1 孔隙度

文中根据室内三轴试验，在围压0.8 MPa的条件下，分别设定孔隙度为0.2，0.25，0.3，0.35以及0.4下的数值三轴试验，试样生成的颗粒个数见表3，其应力-应变曲线见图3.

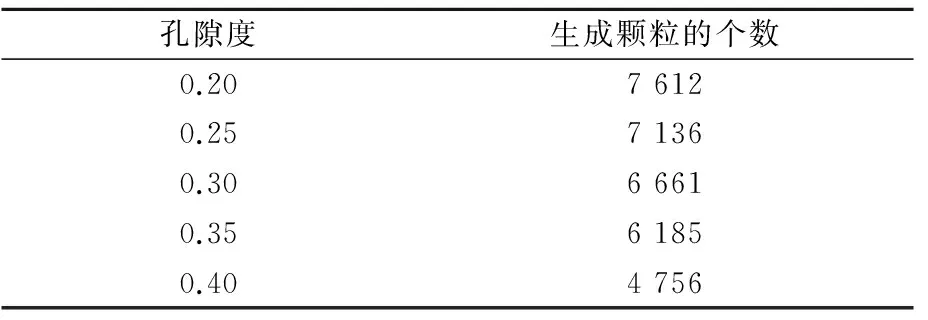
表3 不同孔隙度下模型内颗粒的个数

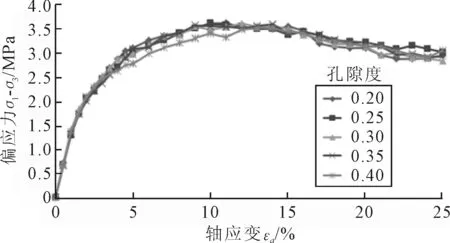
图3 正常固结条件下不同孔隙度下的应力-应变曲线

刘勇等[10]得出随着孔隙度的增大，土体峰值强度明显减小，且在孔隙度为0.45时，模型明显表现出体缩效应.文中研究在不用孔隙度条件下的土体宏观力学反应.由图3可知，在初始应力为正常固结的情况下，随着孔隙度的增大，模型峰值强度减小不明显.此时由于试样在生成颗粒之后得到了充分固结，因此剪切初始应力状态一样.固结后的模型与孔隙度联系较小，而在不同孔隙度下试样均表现出应变软化的现象，根据应变软化型破坏试样的机制可知，试样内部出现剪切面，从细观角度分析孔隙度对试样宏观特性的影响.

图4 不同孔隙度条件下的颗粒转动速度场

由图4颗粒转动速度场可知，标定为白色的颗粒为转动速度大于0.11 rad/s的颗粒，白色的颗粒反应了剪切面的分布情况.因此，围压0.8 MPa不同孔隙度下模型中试样均形成了剪切面，但根据三维坐标可知，不同的孔隙度试样破坏形成的剪切面空间分布不同.已知试样密度与试样孔隙度相关，在不同密度条件下，试样的破坏面空间分布不同.

3.2 配位数

初始配位数是指模型在生成过程中已经设定了的颗粒间的接触数.初始配位数最大，表明初始模型颗粒越紧凑，在一定的孔隙度条件下，颗粒生成的数量也就越多.从上述孔隙度对模型材料的宏观力学特性的影响可以得出，生成颗粒的数量(由不同的孔隙度引起的)对材料峰值强度基本没有影响，而对材料的剩余强度有一定的影响，但影响不大.基于此，在分析配位数对材料宏观力学特性的影响时推测，其影响与孔隙度的影响大致相同.图5为不同初始配位数下的应力-应变曲线.

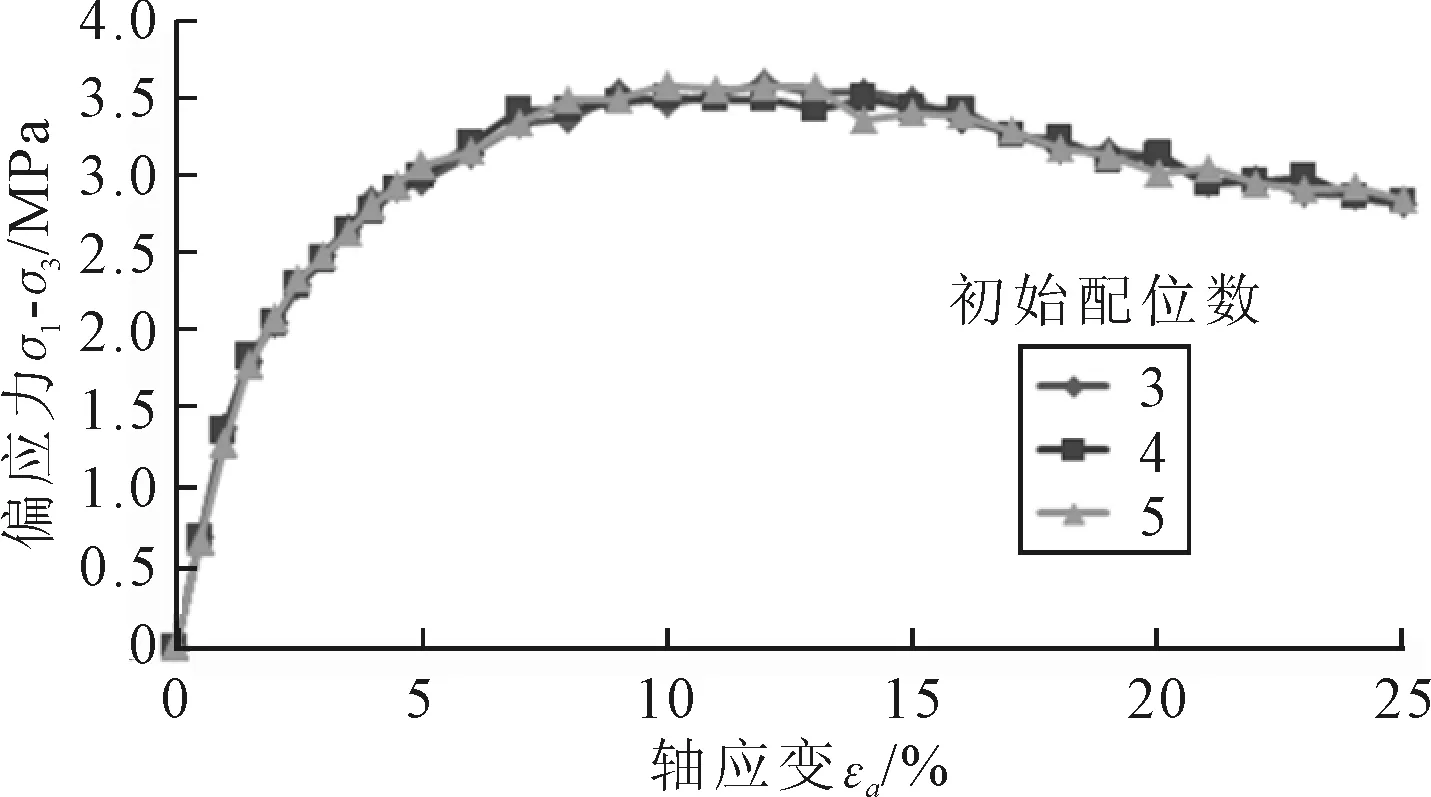
图5 不同初始配位数下的应力-应变曲线

不同初始配位数对数值模型中粗粒土宏观力学特性几乎没有影响.由图5可知，不同初始配位数对材料的峰值强度没有影响，对剩余强度影响不大.不同的颗粒初始配位数导致了试样的应变软化现象，根据颗粒位移场机制可知试样内部均出现了剪切面.从细观角度分析不同颗粒初始配位数下颗粒转动速度场的变化情况，不同的初始配位数造成试样剪切破坏面空间分布不同.初始配位数为3时的颗粒转动速度场与初始配位数为4时的完全相反，而初始配位数为5时亦不相同.初始配位数影响颗粒数量的生成，也影响大颗粒数量的生成和分布.而大颗粒的空间位置分布不同，又影响剪切面的分布和走势.因此，初始颗粒配位数对于材料的峰值强度以及剩余强度影响较小，对于材料的破坏面分布影响较大.

3.3 法向刚度与切向刚度比

kn/ks是颗粒法向刚度与切向刚度之比.改变颗粒的竖向接触刚度与切向接触刚度之比，得到在围压0.8 MPa下不同kn/ks的应力-应变曲线图，见图6.

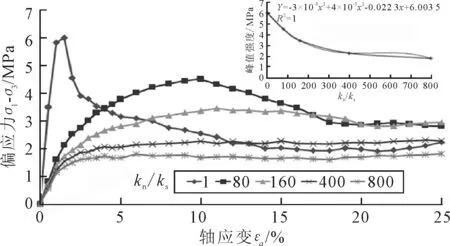
图6 不同kn/ks值下的应力应变曲线

由图6可知，随着kn/ks的不断增大，土体峰值强度不断减小，峰值强度对应的轴应变在不断增大，kn/ks与试样峰值强度的关系式为

y=-3e-8x3+4e-5x2-0.022 3x+6(2)

式中：x为kn/ks，试样模型逐渐从应变软化型向应变硬化型转变.随着切向刚度不断减小，切向抗变形能力下降；随着kn/ks的不断增大，试样的破坏形式从形成剪切面转变成以侧向应变为主的破坏形式.根据颗粒转动速度场进行分析，随着kn/ks的增大，转动速度较大的颗粒逐渐减少，剪切面分布不明显.kn/ks为80时，转动速度较大的颗粒组成的剪切分布比较明显，当kn/ks值增大到400，发现试样内部没有剪切面的形成.颗粒切向刚度逐渐减小，试样破坏主要以圆周型侧向向外扩散为主，转动速度较大的颗粒均匀分布在试样内部，试样抗剪强度降低主要是试样切向抗变形能力下降导致的.而kn/ks值较大时，应力应变曲线呈应变硬化型主要是由于试样圆周型侧向破坏为主而无法形成剪切面导致的.

3.4 颗粒粒径分布

根据加权平均数颗粒粒径11.066 25 mm，设定不同的颗粒最小半径，计算得表4的数据.

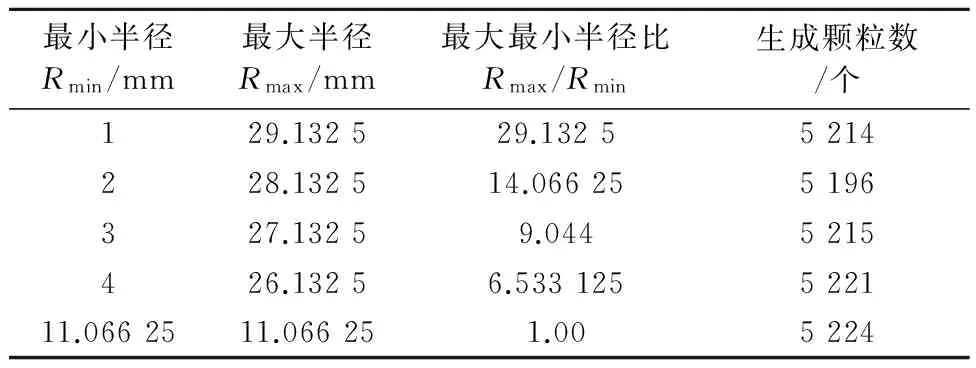
表4 颗粒最小半径和颗粒最大最小半径比确定表

由表4可知，计算各不同最小颗粒半径条件下的试样三轴试验，分析粒径分布情况对抗剪强度的影响，见图7.

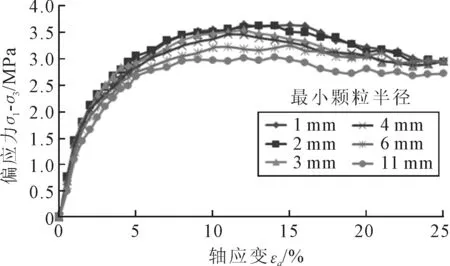
图7 不同最小颗粒半径下的应力-应变曲线

由图7可知，当试样颗粒粒径的加权平均数为11.066 25 mm时，随着颗粒最小粒径的增大，试样的峰值强度逐渐减小；最小颗粒粒径在0.1～1 mm波动时，试样颗粒粒径对试样抗剪强度的影响较小；但随着最小颗粒粒径不断增大，模型中颗粒粒径的分布对试样抗剪强度的影响增大.这是因为在生成的模型中最小颗粒粒径值很小时，大小颗粒间的咬合较为紧密，尤其是在加载一段时间后，颗粒经过挤压和错动，有利于接触力的传递以及摩擦力的生成.

结果显示，随着最小颗粒粒径不断增大，转动颗粒的分布差异较大；其中11 mm时颗粒粒径相同，但试样破坏不明显.图8为转动颗粒，可以看出转动颗粒越来越少，这是由于在粒径相同的模型内，颗粒间接触力的分布与一般有相对大颗粒模型内的接触力分布不同，内部破坏裂隙均匀分布在模型内.根据应力应变曲线可知，最小颗粒粒径不仅影响着试样内部的应力路径，也影响着剪切面的形成以及试样应变类型.

图8 不同最小颗粒粒径下的转动颗粒

3.5 剪切速率

室内试验和数值试验的宏观反应对加载速率敏感，通常选择一个足够慢的加载速率确保试样在加载过程中处于准静态状态.准静态状态是设置墙体一系列的常量速度后，通过应变控制法实现，且这种状态在一定临界速度内都均适用.文中设置加载速率为0.5 mm/min进行数值模拟，设定不同的加载速率进行研究.

图9为不同剪切速率下的应力-应变曲线.由图9可知，剪切速率对模型中的粗粒土抗剪强度影响很大，随着剪切速率的增大，峰值强度不断增大.实验室内选择较低的剪切速率进行三轴剪切试验，首先是因为实验室内的仪器的限制，其次是试样在准静态状态下的剪切强度最能反映堆石坝或野外滑坡土体的抗剪强度.而在很大的剪切速率下，其剪切类似于滑坡体受到地震或库水位急剧下降或上升等地质灾害条件下的剪切，对土体的力学特性分析没有多大的意义.

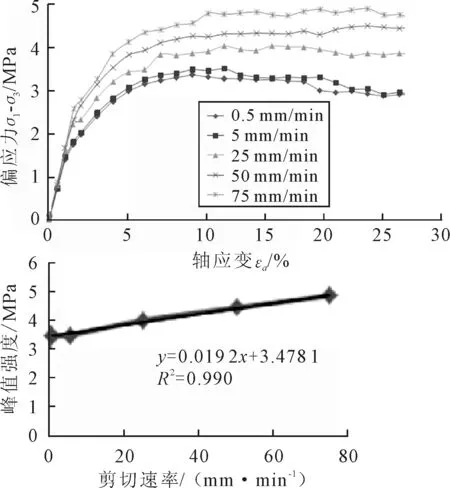
图9 不同剪切速率下的应力-应变曲线

根据不同的剪切速率得到不同的土体抗剪强度峰值，它们之间的关系为

σp=0.019 2v+3.478 1(围压0.8MPa)

(3)

式中：σp为峰值强度，MPa；v为剪切速率，mm/min.

在不同剪切速率下的颗粒转动速度场，随着剪切速率增大，试样破坏不再沿剪切面破坏，试样内部出现大量破坏区.根据剪切速率为75 mm/min的颗粒转动速度场可以看出，试样内部出现了大量的转动颗粒，产生转动颗粒的原因是试样内部出现了大量的剪切裂隙，导致试样“粉碎性”破坏.在剪切速率很大时，试样在压缩剪切过程中不再是准静态过程.

因此，剪切速度不仅影响材料的峰值强度，也影响材料的剩余强度，对材料的破坏的影响最大.

3.6 摩擦系数

在粗粒土研究中，摩擦系数很小时，摩擦角对摩擦系数的敏感度很大，试样的剪切强度摩擦角与摩擦系数呈对数关系.且摩擦系数在0.1～0.4范围内时，摩擦角增加了 12.21°(12.49°～24.7°)，占摩擦角总增加量的76%，可见在摩擦系数较小时，试样摩擦角受摩擦系数的影响较大.文中分别设置摩擦系数为0.1，0.3，0.5，0.7，0.9和1.1，大范围地分析摩擦系数对材料强度的影响，得到摩擦系数与材料强度的关系，见图10.

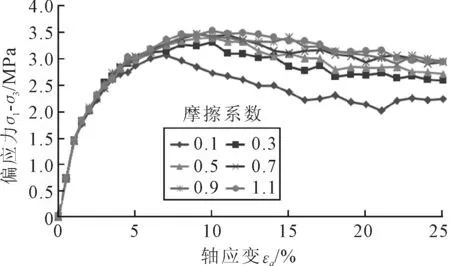
图10 不同摩擦系数下的应力-应变曲线

由图10可知，围压0.8 MPa下摩擦系数对材料的峰值强度影响不大，对材料的剩余强度影响较大.摩擦系数与峰值强度以及剩余强度之间的关系见图11.

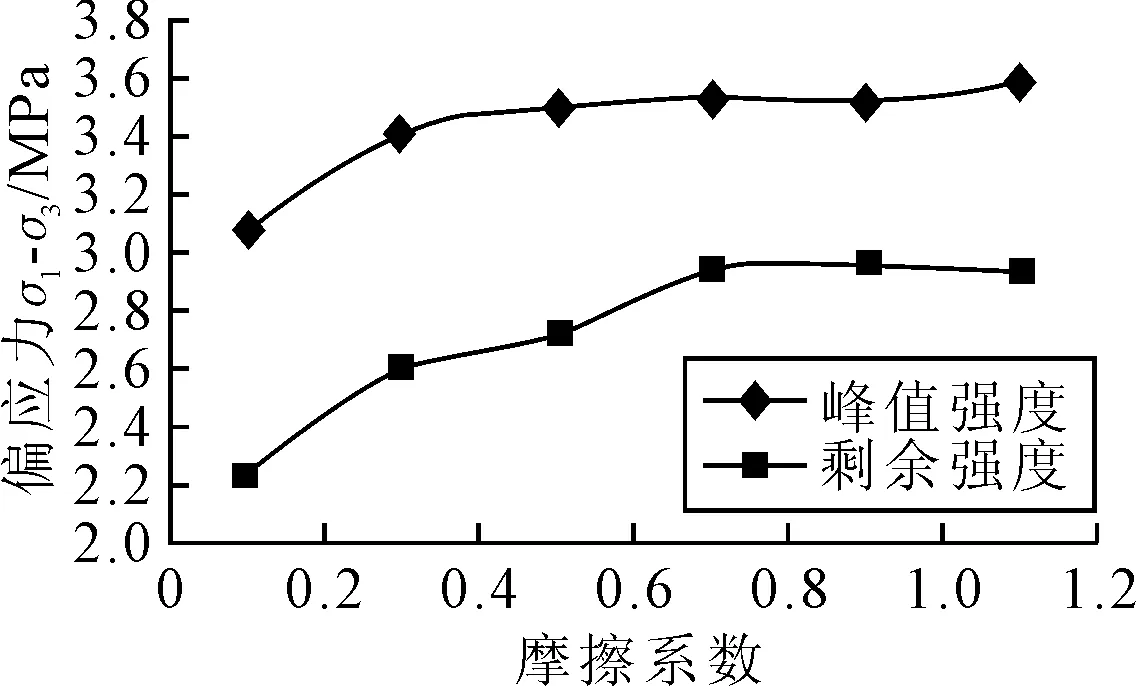
图11 摩擦系数对峰值强度及剩余强度的影响

由图11可知，材料抗剪峰值强度随摩擦系数增大而增大，两者呈线性正相关；剩余强度随摩擦系数增大而增大，当摩擦系数越来越大时，其值对剩余强度的影响越来越小.这与Zhang等[11]对粗粒土进行PFC2D双轴试验结果不同，从校对摩擦系数中发现，摩擦系数对峰值强度的影响因数为2.2，对材料剩余强度的影响因子是2.55，后者大于前者.与二维模拟结果不同，二维离散元材料剪切带形成之后，接触力主要由摩擦力构成，因此二维离散元中摩擦系数对于剩余强度的影响较大；三维离散元中，材料剪切带形成以后，由于三维立体颗粒间挤压与错动，颗粒并不会像二维模型中的颗粒因剪切带形成而分开.围压的存在致使颗粒间的接触力由摩擦力、侧向接触力以及竖向接触力组成，所以在三维离散元中，影响剩余强度的因素不仅有摩擦系数.

从细观颗粒的摩擦系数角度，对试样破坏形式进行分析可知，观察其剪切结束之后的颗粒转动速度场，在不同摩擦系数下，剪切面走向基本相同；转动速度较大的颗粒基本围绕在剪切面附近，且随着摩擦系数增大，试样剪切面厚度不断增大.这是由于颗粒间的摩擦力越来越大，剪切面附近的颗粒在发生平移和转动过程中会带动其周围的颗粒一起运动，所以从外观上看剪切面增厚.

4 结 论

1) 基于数值试验结果能够很好的拟合室内试验结果，以应力-应变曲线为粗粒土宏观力学特性研究对象，得出各细观参数对粗粒土抗剪峰值强度以及剩余强度的力学敏感性排序为：kn/ks>摩擦系数>剪切速率>颗粒粒径分布>孔隙度>配位数.

2) 从细观角度出发，根据模型中的颗粒位移场以及颗粒转动速度场对各细观参数对粗粒土三轴模型变形，以及破坏面空间分布进行分析，得到各细观参数对粗粒土三轴模型变形敏感性结论：剪切速率>kn/ks>颗粒粒径分布>孔隙度>配位数>摩擦系数.其中摩擦系数对材料破坏面的空间分布基本没有影响，但影响着破坏面的厚度.

[1]邓益兵,周健,刘文白,等.螺旋挤土桩下旋成孔过程的颗粒流数值模拟[J].岩土工程学报,2011,33(9):1391-1398.

[2]MATTHEW E T, STEVE C, ZHAO X L, et al. Visualization and analysis of microstructure in three-dimensional discrete numerical models[J]. Journal of Computing in Civil Engineering,2009,23(4):277-287.

[3]黄彦华,杨圣奇.非共面双裂隙红砂岩宏细观力学行为颗粒流模拟[J].岩石力学与工程学报,2014,33(8):1644-1653.

[4]丛宇,王在泉,郑颖人,等.基于颗粒流原理的岩石类材料细观参数的试验研究[J].岩土工程学报,2015,37(6):1031-1040.

[5]唐文帅.离散元细观参数对粗砂变形性质的影响[J].水利科技与经济,2015,21(2):32-34.

[6]陈亚东,于艳,佘跃心.PFC3D模型中砂土细观参数的确定方法[J].岩土工程学报,2013,35(2)：88-93.

[7]耿丽,黄志强,苗雨.粗粒土三轴试验细观模拟[J].土木工程与管理学报,2011,28(4):24-29.

[8]HUANG H Y. Discrete element modeling of tool rock interaction[D]. Minnesota: University of Minnesota,1999.

[9]NARDIN A, SCHERFLER B A. Modeling of cutting tool soil interaction part II： macro-mechanical model and up scaling[J].Computer Mechanics,2005,36(5):343-359.

[10]刘勇，朱俊樸，闫斌.基于离散元理论的粗粒土三轴试验细观模拟[J].铁道科学与工程学报,2014,11(4):58-62.

[11]ZHANG Z H, ZHANG G D, LI X L, et al. The shear dilation and shear band of coarse grained soil based on discrete element method[J]. Advanced in Civil Engineering and Transportation IV,2015(7):679-685.

Sensitivity Analysis of Triaxial Test of Coarse Grained Soil Based on PFC3D

LI Can QIU Hongsheng ZHANG Zhihua

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)

This paper uses PFC3D as the tool and using weighted average particle size distribution method to build model. The parameters including porosity, coordinate number, kn/ks, particle size distribution, shear rate and friction coefficient are chosen as the micro parameters to analyze the sensitivity. The stress-strain intensity curve is taken as the mechanics analysis method and the particle rotation velocity field is used as deformation analysis method. The sensitivity of each parameter to the strength of the coarse grain is sorted. The effect of the shear failure of coarse grained soil is summarized and analyzed. The research shows that the parameters in the model have a certain effect on the strength and deformation of coarse grained soil and the kn/ks has the greatest influence on the strength and deformation of coarse grained soil, while the porosity and coordinate number have least influence.

PFC3D; micro parameters; particle rotation velocity field

2016-09-05

*国家自然科学基金项目资助(51308429)

TU411 doi:10.3963/j.issn.2095-3844.2016.05.021

李灿(1991- )：男，硕士生，主要研究领域为岩土及隧道工程衬砌灾害防控