特定条件下相对动点的动量矩定理的简洁形式及其应用
2016-11-14任述光吴明亮谢方平
任述光吴明亮谢方平
(1湖南农业大学工学院,湖南长沙 410128;2湖南省现代农业装备工程技术研究中心,湖南长沙 410128;3南方粮油作物协同创新中心,湖南长沙 410128)
特定条件下相对动点的动量矩定理的简洁形式及其应用
任述光1吴明亮2谢方平3
(1湖南农业大学工学院,湖南长沙 410128;2湖南省现代农业装备工程技术研究中心,湖南长沙 410128;3南方粮油作物协同创新中心,湖南长沙 410128)
理论力学教材中,刚体平面运动微分方程是利用质心运动定理结合相对质心的动量矩定理导出的,其对于解决刚体平面运动动力学问题提供了普遍的方法,但在有些情况下,采用其他形式的平面运动方程可以更为简洁.为提高特定条件下应用平面运动微分方程解题的效率,给出了质点系相对动点的动量矩定理的一般形式,结合质心运动定理,得到平面运动微分方程的其他形式.讨论了特殊情况下定理的简化条件及简化形式,举例说明了简化形式的动量矩定理结合质心运动定理在解题中的应用,与一般形式的平面运动微分方程相比,可以使解题过程大为简化.
理论力学;动量矩定理;刚体平面运动;教学研究
1 相对动点的动量矩定理的一般形式
目前国内的经典理论力学教材[1-5]及笔者主编的理论力学教材中[6],一般只给出了对固定点或固定轴的动量矩定理,定理及)应用的前提是矩心O或矩轴z必须是惯性参考系中的固定点或固定轴.该定理有着广泛应用,但在有些情形下,往往感到不便,特别在研究复杂的动力学问题时,如果能用对动点的动量矩定理,则解题过程可以大为简化.关于对动点的动量矩定理的应用,一些学者作过专题研讨[7-9],这些研讨对于提升教学效果是十分有益的.笔者通过对该定理的研讨,系统分析了该定理可以简化的条件和简洁形式.限于篇幅,下面简单地给出质点系相对动点的动量矩定理,然后讨论它能够简化的条件.
设有作任意运动的由n个质点组成的质点系,任选其中一动点O′为基点,取随同O′平动的动参考系O′x′y′z′.将质点系的绝对运动分解为随同基点O′的平动和相对于基点O′(即相对于平动的动参考系O′x′y′z′)的相对运动.设任一瞬时,O′的加速度(亦即平动动参考系O′x′y′z′)的加速度为ao′,在各个质点上虚加牵连惯性力FIi= -miao′后,将惯性力系向质心简化,得作用于质心的主矢F′IR,惯性力偶矩为零.虚加惯性力后,可将平动动参考系O′x′y′z′视作惯性参考系,并对O′点应用质点系对固定点的动量矩定理

上式还可写成
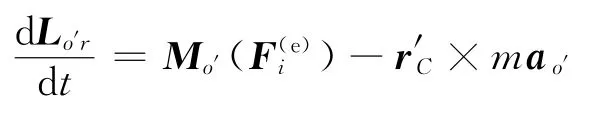
2 定理简化的条件及形式
由上式可以明显看出,在下述3种情况下,等式右端第二项等于零.
1)取质心C为基点.这时r′C为零矢量,因此不论质心的加速度如何,右端第二项恒为零,因此有
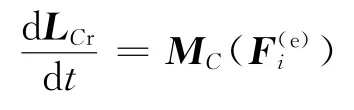
这就是相对质心的动量矩定理,即质点系相对于质心的动量矩对时间的导数,等于外力系对质心的主矩.一般的理论力学教材中,刚体平面运动微分方程给出的就是相对质心的动量矩定理与质心运动定理的两个投影方程的组合.
2)取加速度为零的点A为基点,这时F′IR= -m aA=0,因此

3)取加速度矢量通过质心的Q点为基点,这时r′C与ao′共线,即有r′C×m ao′=0,因此
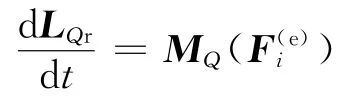
以上3种情况,质点系相对于动点的动量矩定理表达式中,都消去了包含牵连惯性力的附加项,从而形式上与对定点的动量矩定理相同.显而易见,在这些情况下应用相对动点的动量矩定理,可以方便计算.
其中第1种情况应用较多,比如刚体平面运动微分方程就是质心运动定理与相对质心的动量矩定理的结合,在此不再赘述.现在分析第2种和第3种情形的应用.
第二种情形下,取加速度为零的点也即加速度瞬心为矩心.一般情况下,平面运动刚体加速度瞬心的位置不易分析出,但在一些特殊情形下可以简单确定加速度瞬心的位置[10].
第三种情形下,取加速度恒通过质心的点为矩心.可以证明,如果平面运动刚体速度瞬心到质心的距离恒保持不变,则速度瞬心的加速度是通过质心的[11].
3 应用示例
例1 长为l,质量为m的均质杆AB,A端放在光滑的水平面上,B端系在BD绳索上,如图1(a)所示,当绳索铅垂而杆静止时,杆与地面的夹角φ=45°,当绳索突然断掉,求绳断后的瞬时杆A端的约束力.

图1 均质杆受力图
解 研究AB杆,BD绳剪断后作平面运动,初瞬时AB杆的角速度ωAB=0.其受力分析如图1(a)所示,由于水平方向没有力的作用,根据质心运动定理可知AB杆质心C的加速度铅垂,而A点加速度方向水平,分别作两点加速度垂线相交于P点,如图1(b),可以证明P点即为加速度瞬心,由相对加速度瞬心的动量矩定理
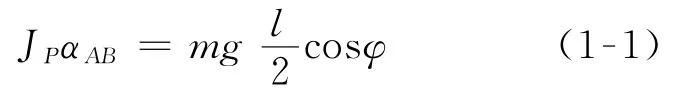
利用转动惯量的平行轴定理
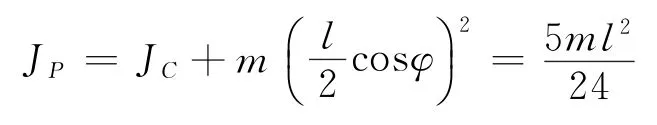
再由相对质心的动量矩定理
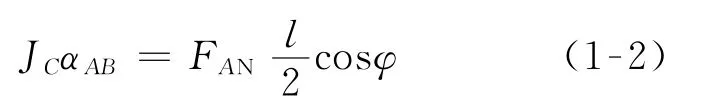
解得

这里只用了两个方程就得到了结果.如果应用平面运动微分方程按常规解法求解可列出两个动力学的方程(因为水平方向无外力),还必须按运动学列补充方程,求解过程就要复杂些.
例2 图2(a)示圆柱体A的质量为m,在其中部绕以细绳,绳的一端B固定.圆柱体沿绳子解开而降落,其初速为零.求当圆柱体下落时其中心A的加速度aA和绳子的拉力FT.

图2 圆柱体受力分析
解 圆轮作平面运动,受力如图2(b)所示.由于运动过程中速度瞬心C与轮的质心A距离保持不变,其加速度通过质心A,故可对瞬心C用动量矩定理,有

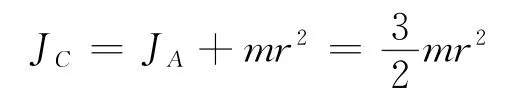
又

再由质心运动定理
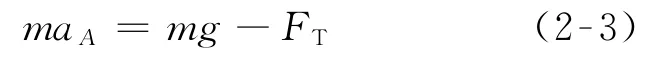
例3 图3(a)示匀质细杆AB质量为m,长为l,在图示位置由静止开始运动.若水平和铅垂面的摩擦均略去不计,试求杆的初始角加速度及A、B两处的约束力.

图3 均质杆受力分析
解 初瞬时杆的角速度为零,A、B两点的加速度分别为水平和铅直,因此P为AB杆加速度瞬心,.由相对加速度瞬心的动量矩定理,有

C点加速度垂直PC连线,由质心运动定理
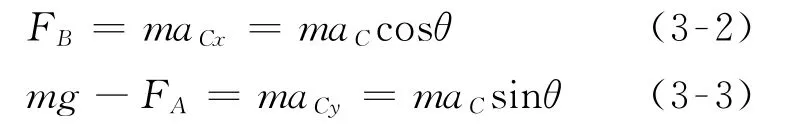
取加速度瞬心P为基点,由加速度合成定理

上式分别向水平和铅锤方向投影可得


此题如果用一般形式的平面运动微分方程求解,需列3个方程,另外还需补充两个运动学方程,这两个运动学方程的补充较之这里的解法复杂.此题若是求运动过程中任意位置杆的角加速度,式(3-1)仍然成立,因为此时P虽然不是加速度瞬心,但它是速度瞬心,且它到质心的距离保持不变,符合第三种情形,只需方程(3-1)就可求解.如果用微分方程一般形式,就复杂多了.但若求两处约束力时,方程(3-2)、(3-3)仍然成立,而(*)式不成立,因为这时P不是加速度瞬心,因此方程(3-4)(3-5)不再成立,需另外分析得到.
例4 均质细杆AB的质量为m,杆长为l,下端A搁在光滑水平面上,上端B用绳索BD系在固定点D上,绳长h,如图4(a)所示.当绳子铅直时,杆的倾角θ=30°,杆端以速度vA向左作匀速运动.求此时杆的角加速度α,绳子的拉力FB和A端需加的水平力F的大小.

图4 均质细杆受力分析
解 可判断图示位置AB杆作瞬时平移,所以vB=vA.因为AB杆的角速度为零,且A点的加速度为零.
取A为基点,如图4(a),有
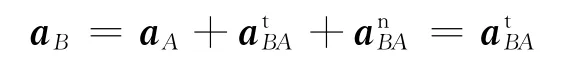
又因为B点作圆周运动,所以

AB杆质心C的加速度

垂直于AB杆,其大小为

应用相对加速度瞬心A的动量矩定理

由质心运动定理

4 结语
本文给出了特殊情形下,对动点的动量矩定理的简化形式.对于运动的质点系,质点系对质心,对加速度瞬心及加速度恒通过质心的点,动量矩定理有与相对固定点的动量矩定理相似的简洁形式.对于一些复杂的动力学问题求解,可用相对加速度瞬心或相对加速度恒通过质心的动点的动量矩定理代替相对质心的动量矩定理,以起到简化求解过程的目的.
一般现有的理论力学教材中没有这个内容,本文提到的这个方法对于学生快速解题有一定效果,以期作为教辅或教师教学参考之用.
[1]李俊峰,张雄.理论力学[M].北京:清华大学出版社,2010.
[2]刘又文,彭献.理论力学[M].北京:高等教育出版社,2006.
[3]哈尔滨工业大学理论力学教研组.理论力学Ⅰ[M].北京:高等教育出版社,2009.
[4]梅凤翔,尚玫.理论力学Ⅰ[M].北京:高等教育出版社,2012.
[5]洪嘉振,杨长俊.理论力学[M].北京:高等教育出版社,2012.
[6]任述光,王业成.理论力学[M].北京:中国农业出版社,2014.
[7]梅凤翔,关于对动点的动量矩定理[J].力学与实践,2011,33(3),67-69.
[8]朱仁贵.对动点的动量矩定理在刚体平动中的应用[J].力学与实践,2013,35(3),81-82.
[9]邱支振.对速度瞬心的动量矩定理的教学与应用[J].安徽工业大学学报,2001,18(3):105-106,119.
[10]许政,王庆.平面运动刚体加速度瞬心的确定及应用[J].大学物理,2004,23(4):5-7,38.
[11]郑权旌.工程动力学[M].武汉:华中理工大学出版社,1987.
MOMENTUM THEOREM OF MOVING POINT IN CERTAIN CONDITIONS
Ren Shuguang1Wu Mingliang2Xie Fangping3
(1Institute of technology,Hunan Agricultural University,Changsha,Hunan 410128;2Hunan Provincial Engineering Technology Research Center for Modern Agricultural Equipment,Changsha,Hunan 410128;3Collaborative Innovation Center of Grain and Oil Crops in South China,Changsha,Hunan 410128)
In theoretical mechanics textbook,the differential equation of the plane motion of rigid body is derived from the theorem of the motion of mass center combined with the moment of momentum theorem for the relative mass center.It provides a common method for solving the dynamic problem of plane motion of rigid body.But in some cases,the use of other forms of planar motion equation can be more efficient.In order to improve the efficiency of solving problem with the application of planar motion differential equation,the general form of the moment of momentum theorem of moving point are conducted.Combing center of mass movement theorem,other forms of planar motion differential equation can be obtained.Under special circumstances,the simplified form of the theorem and relevant conditions are discussed. The simplified form of moment of momentum theorem combining center of mass movement theorem are illustrated in the application of solving problems.Comparing with the conventional planar motion differential equation,it can greatly simplify the problem solving process.
theoretical mechanics;the moment of momentum theorem;plane motion of rigid body;teachingand research
2016-02-16;
2016-03-23
湖南农业大学力学课程教改研究项目(项目编号:9202922).
任述光,男,副教授,主要从事力学教学科研工作,研究方向为工程力学及计算固体力学.shgren2005@aliyun.com
任述光,吴明亮,谢方平.特定条件下相对动点的动量矩定理的简洁形式及其应用[J].物理与工程,2016,26(4):92-95.
