弦横振动方程推导中常用近似的教学改进
2016-11-14郑勇
郑 勇
(黔南民族师范学院物理与电子科学学院,贵州都匀 558000)
弦横振动方程推导中常用近似的教学改进
郑 勇
(黔南民族师范学院物理与电子科学学院,贵州都匀 558000)
数学物理方法课程中弦横振动方程的常见推导方法都是在“横振动假定”基础上进行,为得到振动方程的形式,往往需要引入较为复杂的三角函数近似和弦中张力不变等近似处理.本文通过分析发现,若充分利用由“横振动假定”得到的弦中张力纵向分量处处平衡的结论,不对这一结论做近似处理,反而能够更简单地完成推导.进一步分析比较了两种推导方法的合理性,发现两种推导方法,甚至“横振动假定”,都只在小幅横振动条件下成立.
弦;振动方程;近似
推导轻弦横振动方程往往是数学物理方法课程教学中必不可少的一个教学内容,但是教学难度并不低.究其原因,主要在于推导过程中用到一些很难让初学者信服的近似,比如,在各种版本的数学物理方法教材[1-5]中,在建立方程时都要假定弦内张力在振动过程中保持不变,还要用到诸如“sinα≈tanα”的近似,以便引入导数建立方程.虽然在小幅振动时这些近似都是合理的,但是初学者接受起来往往并不容易.寻求更适合课堂教学的推导方法是必要的.
为此,我们对该部分教学内容作了仔细分析,发现其实只需要对教科书中常见的推导过程稍加改进,就可以极大地改善推导过程的严密程度,而且还更为简洁明了.值得注意的是,我们这里所说的“改进”主要是教学层面的;事实上,在后面部分我们将看到,本文给出的推导方法与教材中常用的推导方法都只有在微小振幅时才成立,二者并无本质区别.为方便说明,先将各种教科书中常用的推导方法列出,再在此基础上作进一步阐述.
1 弦横振动方程教材常见推导
一般来讲,弦横振动方程的推导过程都是采用微分的思想基于质点动力学进行的,最基本近似是认为“弦上各点只做横向运动,无纵向运动”,这是导出横振动方程的基础.对于一根振动前沿x方向绷紧放置的轻弦,静止状态时其中张力记为T0;作微小横振动时各处的横位移为u(x,t).
如图1所示,取出位于区间(x,x+ d x)内的一小段弦元进行分析,其两端张力分别为T1、T2,与x轴方向夹角分别为成α1、α2.根据其在x轴方向(纵向方向)和横向方向受力情况,利用牛顿第二定律有:
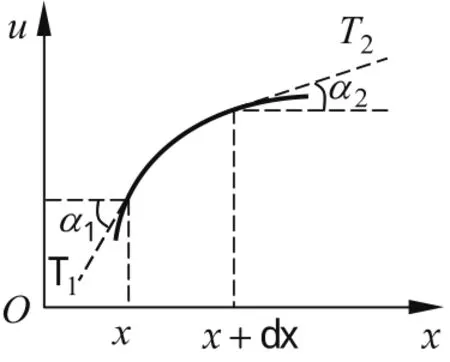
图1 振动弦元受力分析
纵向方向:

横向方向:

其中ρ为弦静止时的线密度.
接下来的步骤就是近似处理.
一般都会用到两个近似[1-5]:一是将式(1)中cosα近似用1代替,相当于认为振动过程中弦中的张力处处相等,记为T;二是将式(2)中的sinα近似地用sinα≈tanα=ux(x,t)代替,最终得到

稍加整理就得到振动方程的形式

与和振动方程的一般形式utt-a2uxx=0(a为常数)比较,我们需要将振动过程中弦中张力T视为常数或保持不变.
纵观上述整个推导,将sinα≈ux(x,t)最不易让初学者接受;另外认为振动过程中弦中张力处处相等或保持不变也往往让初学者费解,毕竟振动时弦上各处的拉伸程度是有差别的,根据“弦上各点只做横向运动,无纵向运动”的“横振动假定”或式(1),也只能得到张力纵向分量处处相等的结论.那么有没有更好的办法呢?稍加分析就可用如下思路进行改进.
2 严格基于横振动假定的推导
事实上,如果不对式(1)作近似处理,直接从张力在纵向方向分量处处平衡,即T2cosα2= T1cosα1=T纵出发,易知:T2=T纵/cosα2,T1= T纵/cosα1,式(2)变为
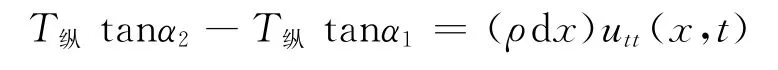
即:
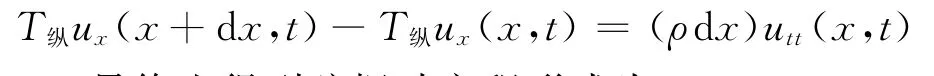
最终也得到弦振动方程形式为

唯一区别在于式(3)中的张力在这里是其纵向分量T纵.与振动方程的一般形式utt-a2uxx=0(a为常数)比较,需要将张力的纵向分量视为常数,这也与由“横振动”假定或式(1)推知的T纵与x无关的结论相符.因此,与一般推导中将弦中张力T视为常数比较,显然将张力的纵向分量视为常数更为“合理”;不过在后面讨论部分将看到,将T或T视为常数都只有在微小横振动时成立,两种做法并无本质区别.
3 比较分析
比较两种推导不难发现,两种推导最大不同在于对式(1)的处理:将弦中张力T视为常数,还是将张力的纵向分量视为常数.教材中一般的推导相当于是从描述弦上“张力纵分量处处相等”的式(1)出发,利用“cosα=1”得出“弦振动时张力处处相等”的结论,而后面处理式(2)不得不将sinα≈tanα才能得到导数ux,以便进一步得到振动方程形式.而我们的推导相当于未对式(1)作近似处理,处理式(2)自动得到tanα或ux,反而更简单.这样,通过细小的改进,使得通常推导中需要认为弦中张力处处相等,以及需要将sinα近似为tanα的两处让初学者费解的近似都不再需要,自然更适合教学.
4 讨论
显然,得到式(4)的推导在“弦上各点只做横向运动,无纵向运动”的基本假定下是严格的.因此,可以更好地去分析这一假定的合理性.
仍以位于区间(x,x+d x)内的一小段弦元为例,若其原长为d x0,静止时张力其中Y和S分别为材料的杨氏模量和弦的横截面积.振动过程中弦元长度变为

张力变为

若将该弦元与x轴夹角记为α,则易知
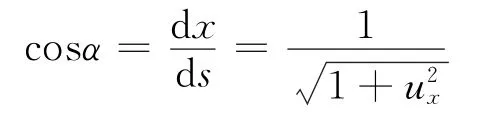
张力的纵向分量为

由于横振动时ux与x有关,弦上各处的张力以及其纵向分量显然都与x有关.我们看到,弦作横振动时,张力纵向分量在弦上各处并不完全相等;此时弦上各点除了横振动必定还会出现纵向运动.换句话讲,纯粹的横振动是不存在的.但是在小幅横振动时,ux是小量,1+u2x≈1,T纵≈T0,纵向运动可以不作考虑.同时看到,此时,T≈T0.即,小幅横振动时,弦中各处张力以及张力的纵向分量的确都可视为常数.
因此,弦横振动假定[或式(1)]本身就是一个近似,只有在小幅横振动时才成立.就弦横振动方程的推导而言,无论是一般教材中的推导还是本文给出的推导过程,都是在该假定基础上进行的,显然也只适用于小幅横振动情形——此时,弦中各处张力、张力的纵向分量都可近似视为常数,两种推导方法并无本质区别.对振幅较大情形,弦纵向方向运动不可忽略,横振动假定不再合理,两种推导方法都不再适用.关于作横振动的弦其纵向运动情况文献[5]中已有讨论,我们不再多述.
[1]梁昆淼.数学物理方法[M].4版.北京:高等教育出版社,2010:109-110.
[2]吴崇试.数学物理方法[M].北京:北京大学出版社,1999: 254-256.
[3]姚端正,梁家宝.数学物理方法[M].2版.武汉:武汉大学出版社,1997:124-126.
[4]胡嗣柱,倪光炯.数学物理方法[M].2版.北京:高等教育出版社,2002:177-179.
[5]徐小树,王海燕.对建立弦的横振动方程时的一个近似条件的分析[J].大学物理,1998(7):23-25.
IMPROVEMENT OF THE COMMONLY USED APPROXIMATION IN DERIVING THE TRANSVERSE VIBRATION EQUATION OF A STRING
Zheng Yong
(College of Physics and Electronics,Qiannan Normal College for Nationalities,Duyun,Guizhou 558000)
In the math-physical method course,the transverse vibration equation of a string is commonly derived on the basis of the“transverse vibration assumption”.In order to get the form of the vibration equation,people generally needs an approximately treating of the involved trigonometric function and tension force.In this paper,a new deviation is given with the balance of the longitudinal component of tension force in a string and the fully used“transverse vibration assumption”.Through analysis,we find the derivation procedure can be more simpler if any other approximations are not used.Further analysis shows that these two kinds of deviations,along with the“transverse vibration assumption”are valid only when the vibration amplitude is small.
string;vibration equation;approximation
2016-01-04
基金课题:贵州省教育规划青年课题(2014C031).
郑勇,男,讲师,主要从事基础物理教学及研究工作.zhengyongyb@163.com
郑勇.弦横振动方程推导中常用近似的教学改进[J].物理与工程,2016,26(4):89-91.
