基于SHPB的花岗岩应变率效应分析

李　丹，戚伟伟，王艳华

(安徽新华学院土木与环境工程学院，安徽 合肥 230088)



基于SHPB的花岗岩应变率效应分析

李丹，戚伟伟，王艳华

(安徽新华学院土木与环境工程学院，安徽 合肥 230088)

目的花岗岩做为重要的土木工程材料，其动态力学性能分析意义重大，而目前相关研究成果不足。对花岗岩的动态力学性能进行研究，分析花岗岩冲击压缩下应变率对其动态力学性能的影响，为花岗岩的动态研究提供参考。方法选择合适尺寸的花岗岩试件，利用SHPB压杆装置对花岗岩试件进行冲击压缩实验，得到多组高应变率下入射波、反射波和透射波曲线，根据应力波理论转换为花岗岩试件的应力、应变和应变率随时间变化的关系，进而得到多组花岗岩在不同应变率下的应力-应变关系曲线以及耗散能。结果比较可得，花岗岩试件的冲击压缩极限强度和峰值应变随着应变率的增加而增加，但增幅却有所减小，表明花岗岩延性随着应变率的增大而增大；耗散能和应变能随着应变率的增加也相应增大，而相应的应变能总是比耗散能小而又无限接近。结论花岗岩冲击压缩的动态力学实验结果与静态区别很大，随着应变率的提高，花岗岩试件的破坏应力迅速提高，峰值应力和应变、耗散能都随着应变率的增加而增加，实际工程中在动态荷载作用下，考虑花岗岩的动力性能，能使结构分析结果更加可靠。

花岗岩；SHPB；应变率；耗散能

0　引　言

20世纪初Hopkinson提出分离式霍布金森压杆(split Hopkinson pressure bar，SHPB)装置原型，当时仅能用来测量冲击荷载的脉冲波形。经过Kolsky[1]等人改进后可用来测量材料在冲击荷载作用下的应力-应变关系。众多学者在拓宽SHPB实验研究领域上做了不少工作，并对SHPB实验装置进行有针对性的改进，以满足不同材料的测试需要。例如Lindholm[2]和于亚伦[3]建立了三轴SHPB实验装置；Verleysen[4]推荐直径为25 mm的铝杆进行脆性材料冲击压缩实验。SHPB实验以一维弹性波实理论为基础，是近似实验，学者对这些近似原因也提出了一些改进方法，例如：Follansbee和Frantz[5]利用FFT变换等数学知识对波形弥散进行修正；王永刚[6]在入射杆前增加一个很薄的垫片(通常为黄铜)，软化子弹的撞击，减小波形振荡的幅值，改善了入射波形，有利于试样内部应力均匀；还有相关脉冲整形技术等。然而，尽管研究成果很多，但由于动态实验技术受环境影响因素大，材料动态力学性能与取材等多方面因素有关，使得人们对于这一实验技术的认识不尽相同，不同的研究者对同一种材料进行实验研究，所得到的结果存在较大差异。这已成为制约SHPB实验技术向标准化发展的关键因素。

花岗岩是典型的孔隙材料，这些孔隙的存在严重影响花岗岩的力学、物理和化学等各方面性能。目前利用SHPB实验装置进行花岗岩的动态力学性能研究，存在诸多问题，例如：(1)大尺寸试样所带来的应力平衡、均匀化与波形弥散；(2)试样在应力平衡前的过早破坏；(3)试样的恒应变率加载与变形问题。目前不少学者利用SHPB装置进行花岗岩动态力学性能研究。例如：喻勇[7]利用Hopkinson拉杆研究了岩石拉抻破坏中的能量及损伤特征；戚承志[8]对弹塑性孔隙介质在冲击偏应力张量作用下的行为进行了研究；席道瑛等[9]对SHPB试验得到的实测波形运用拉格朗日分析和路径方法获得了大理岩和砂岩动态本构关系；R．L．Shan等[10]用SHPB实验研究了花岗岩单轴冲击全过程本构特性，得出花岗岩的冲击应力-应变曲线在峰值前具有明显的跃进性；刘剑飞等[11]利用预留间隙法对花岗岩材料实施了高应变率动态试验，研究了花岗岩材料在动态和静态重复加载条件下的力学行为和泊松比；谢和平等[12]从热力学角度出发，结合岩石损伤力学与断裂力学的研究，阐述了岩石变形破坏过程中的能量耗散特点。

本文结合以上SHPB装置的改进技术，在前人研究基础上选定合适尺寸的花岗岩试件进行冲击压缩实验得到了不同应变率下的入射波、反射波和透射波曲线，并运用应力波理论转换为应力、应变和应变率随时间变化的曲线，研究高应变率下花岗岩应力-应变曲线和耗散能随应变率变化的规律，为花岗岩的动力性能研究提供参考。

1　实验原理[13]

SHPB实验的基本原理是细长杆弹性应力波理论。建立在一维弹性波和试件的应力(应变)均匀性2个基本假设上，具体内容可参照应力波相关理论，由此可得：

(1)

F1=EA(εi+εr)

(2)

(3)

F2=EAεt

(4)

式中：u1、u2分别是入射杆、透射杆与试件接触的截面位移；C0为波导杆的弹性纵波波速；F1、F2分别为作用在试件两端的力；E是波导杆的弹性模量；A是波导杆的横截面积。

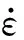
(5)

式中：ls是试件的长度；As是试件的横截面积。按照试件应力均匀性假设，有F1=F2，根据一维应力波理论有：

εi+εr=εt

(6)

利用入射波εi和透射波εt的数据可以得到：

(7)

由此得到试件的应力、应变、应变率随时间变化曲线。

式(5)、式(7)即为传统SHPB实验测量材料高应变率下应力-应变关系的“三波法”和“两波法”。由于SHPB实验中入射杆长，入射波在反射过程中会出现一定程度的波形失真，且对于大直径的SHPB装置更为严重，而试件材质均匀，距离短，滤波效果好，透射波弥散较小，所以通常采用两波法中的入射波和透射波[14]。

根据能量守恒定律，冲击压缩实验试件的耗散能Ws(t)为

Ws(t)=Wi(t)-Wr(t)-Wt(t)

(8)

其中Wi(t)、Wr(t)、Wt(t)分别为入射波、反射波和透射波能量，表达式如下：

(9)

2　实验过程

本次实验选取的是直径为60 mm，厚度为30 mm花岗岩试件共计30余块，进行冲击压缩实验，实验之前，先通过静力试验测得花岗岩的弹性模量等相关数值，做为动态试验的对比资料。动态实验采用直径为74 mm的Hopkinson压杆，借助超动态应变仪和成都中科动态仪器有限公司的PCI多通道高速数据采集系统进行采集数据。最低应变率为试件发生宏观微小裂纹的最低冲击荷载，为10.7 s-1，最高应变率为试件粉碎的最大冲击荷载，为111.9 s-1，分别获得不同冲击荷载下的入射波、反射波和透射波曲线。实验如图1所示。

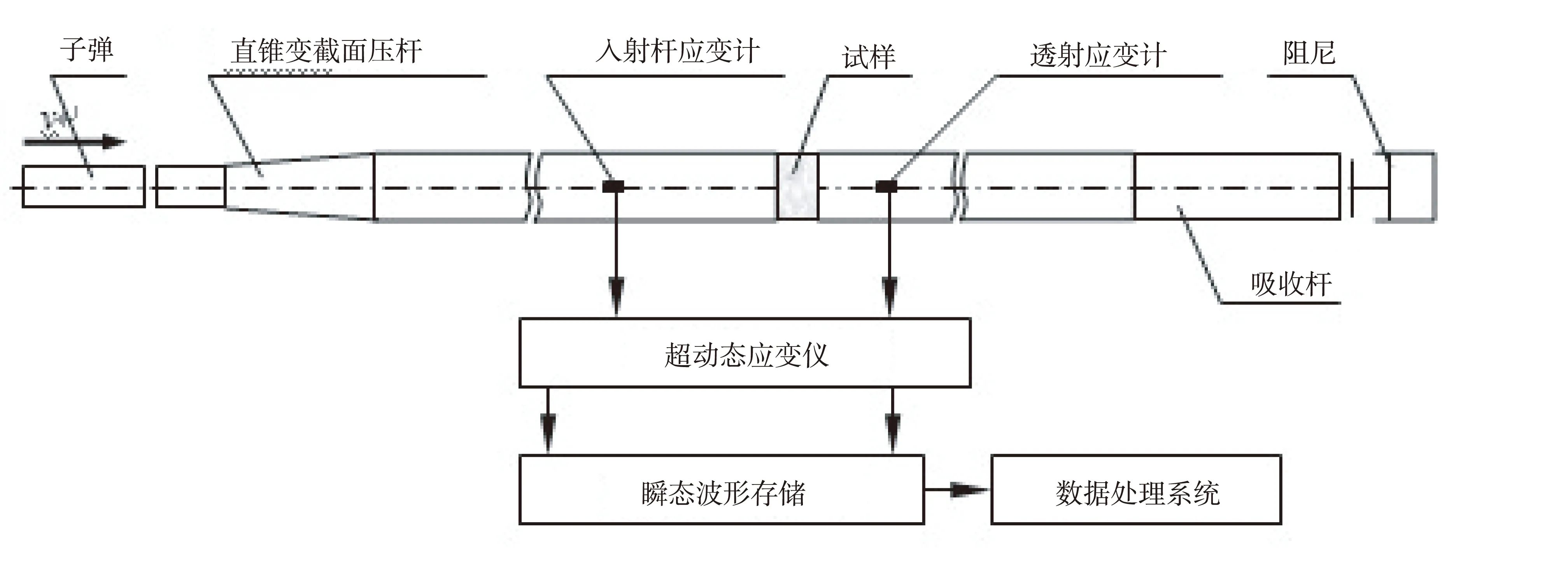
图1　直锥变截面SHPB装置进行冲击压缩试验方案

实验时，为防止应变计信号有误，在入射杆粘贴2个应变片，透射杆粘贴1个应变片，每个试样相隔180 °，两处位置分别粘贴1个90 °应变花，分别测量该点的轴向和横向应变，利用半桥电测技术，抵消温度影响。典型信号采集如图2所示。

图2　花岗岩SHPB实验数据采集

3　数据处理及分析

根据应力波理论，实验曲线在达到应力平衡之前数据不满足条件，所以数据处理时去除前面上升段部分数据后，其余阶段数据效果较佳。实验完成后，采集得到花岗岩应变随时间变化的曲线，数据进行处理可得出不同应变率下应力和应变随时间变化曲线，总计30余个，分成7组，每组应变率相近，对每组应变及相应的应力取平均得到不同应变率下的应力-应变曲线，如图3所示。

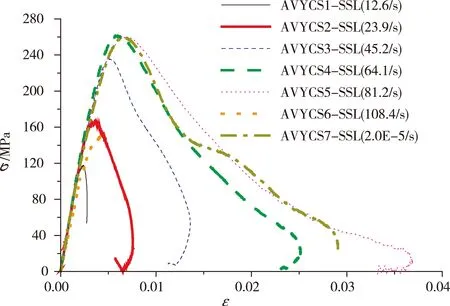
图3　花岗岩不同应变率下平均后的应力-应变曲线

编号ε·/1/sσb/MPaεb/10-6第一组12.61182327第二组23.91653592第三组45.22365060第四组64.12616008第五组81.22606903

(1)应变率对峰值应力和峰值应变的效应分析

在不同的变形速率(应变率)下，大多数材料的力学性能会发生不同程度的改变，材料的这种属性称为应变率效应。对每组应力-应变曲线提取最大应力及对应的应变，由于在后2组中的应变率过高，花岗岩粉碎，数据畸变严重，故只取其中前5组，如表1所示。可得：1)花岗岩的冲击压缩极限强度随着应变率的增加而增加，但增幅却有所减小[15]。准静态实验花岗岩抗压强度为55 MPa，据此，该实验表明花岗岩在单轴动态压缩过程中，抗压强度比准静态大很多，这是由于在动态过程中荷载输入快，材料本身响应有一定的延时导致，但是随应变率增大，其抗压强度不是无限制增大，而是增幅逐渐变缓最后趋近与1个稳定值260 MPa，这与实际相吻合。2)花岗岩峰值应变随着应变率的增加而增加，增幅也有所减少，但趋势不明显。峰值应变反映是花岗岩的脆延性指标，这表明动态过程中花岗岩延性随着应变率的增大而增大，增大的幅度有所减小。

(2)应变率对耗散能的效应分析

表2　不同应变率下的耗散能和应变能平均值

根据式(8)和(9)，编写相应的Fortran语言计算得到花岗岩的耗散能，通过应力-应变曲线积分得到花岗岩的应变能。为使数据可靠，对相近应变率下的耗散能和应变能取平均，如表2所示。可见，随着应变率的增大，耗散能和应变能也相应增大，而相应的应变能总是比耗散能小而又无限接近[16]。这是由于在试样变形破坏过程中，耗散的能量包括应变能、塑性能、产生裂纹的热能及质点的动能诸多形式，其中主要为应变能。随着应变率的增大，耗散能中的其它能量占总值逐渐减小，故在高速应变率下，可近似认为耗散能与应变能相等。

4　曲线模拟

(1)极限强度随应变率变化的曲线模拟

岩石强度是评价岩石工程稳定性的重要参数之一。在动力条件下，材料的抗拉及抗压强度与静力条件下的数值差异很大，因此必须考虑强度对于应变率的依赖行为。

由表1可知，试样的抗压强度随着应变率的增加而增加，但是其增加的幅度却是略有减小。考虑到建立函数关系时，量纲一致性，故分别以第一组数据为参考，得出相对抗压强度和相对应变率，由对数函数、指数函数、幂指数函数等多次曲线模拟，得出唯有幂指数函数相关度最大，故选取幂指数函数建立相对抗压强度和相对应变率的关系，如图4。

图4　花岗岩冲击压缩强度与应变率关系

其中，γ=2.27，α=-2.29,β=-1.78。相关度R2=0.9864。由于数据是根据花岗岩动态实验所得，故模拟的该曲线只能在一定的应变率下才能使用，根据关系式，当相对应变率小于1时，花岗岩相对抗压强度可能为负值，显然不对。

(2)峰值应变随应变率变化的曲线模拟

峰值应变与应变率的关系可以反映花岗岩的延性，由表1可知，试样的峰值应变随应变率的增大而增大，减小趋势不明显。同样对其相对值进行曲线模拟，得到图5。

图5　花岗岩冲击压缩峰值应变与应变率关系

函数关系式为：

其中，γ=10.17，α=-9.45,β=-22.95,相关度R2=0.987。

(3)应变能随应变率变化的曲线模拟

韧性与材料从加载到破坏过程中吸收能量的能力有关，因此韧性是材料强度和延性两种指标的综合反映。单纯用延性指标(峰值应变)反映材料的韧性具有一定的片面性，应该采用应变能来衡量。破坏时的应变能密度可以通过对应力-应变曲线的面积积分得到。再乘以试样的体积得到应变能曲线。

现根据花岗岩冲击压缩的应变率，模拟花岗岩冲击压缩应变能与其关系。为使量纲一致性，纵坐标取相对应变能，横坐标去相对应变率，同上，选取合适函数关系使得相关度最大，见图6。

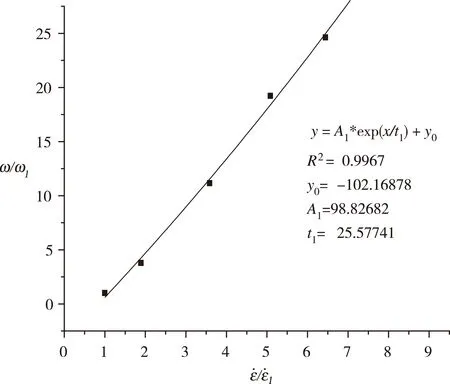
图6　花岗岩冲击压缩应变能与应变率关系

应变能与应变率函数关系式为：

其中，γ=-102.17，α=98.83,β=25.58,相关度R2=0.997。

由以上曲线模拟可见，花岗岩冲击压缩强度、峰值应变、应变能都与应变率有很强的幂指函数关系。以上曲线模拟可作为研究花岗岩应变率效应的借鉴。

5　结论与讨论

从以上分析可见花岗岩材料有很强的应变率效应。破坏应力随着应变率的提高而迅速提高，峰值应力和应变、耗散能都随着应变率的增加而增加。比较动态实验数据和静态实验数据，可以发现部分应变率下动态破坏应力低于静态破坏应力，这是由于动态加载下花岗岩的裂纹数目远大于静态条件下的裂纹数目，因此相应的受动态损伤软化影响程度很大。所以花岗岩材料的动态力学性能的研究要综合考虑应变率的硬化效应和损伤软化效应。大量的冲击试验还表明，不论何种岩石，随着冲击速度(应变率)的提高，其抗压强度也相应增大，但不同岩石增长幅度不同，说明岩石的破碎强度主要取决于应变率和岩石类型。此外，即使静压强度相似的不同岩石，其动态破碎强度也可能存在较大差异，因此，在爆炸与冲击领域内，应采用相应应变率下的岩石破碎强度等动力参数来代替岩石的静态参数，这样更符合实际。

曲线模拟的结果表明花岗岩的抗压强度、峰值应变等都和应变率表现为一定的指数函数和幂函数的关系，而这种关系也决定了它们随着应变率的增加而相应地增加，但是由于实际冲击破坏过程的复杂性，很难找到它们和应变率的一一对应的关系。以上模拟的曲线均是在动态下，因此有其一定的适用范围。

岩石是一种非匀质材料，其结构内部具有位错、裂隙、孔洞、节理和弱面等缺陷[17]，故其承受动荷载下的本构关系和力学特性与承受静载时有很大的差异。而岩石的动态力学特性又具有很大的理论和实际意义，因此对岩石动态力学特性的测试尤为重要。由于岩石本身存在多缝隙，材质不均匀等缺陷，与静力学相比，其动力学问题在实验研究和力学分析上要复杂得多，在物理和数学处理上也困难得多，因此目前岩石类材料在动力实验研究和动力学理论分析上还处于不成熟阶段。在众多动力学问题中，应变率效应和耗散能分析一直是研究材料动态力学性能的重点研究课题。研究的花岗岩动态力学性能实验因受环境、温度等外界影响较大，有其一定的适用范围。本文只是定性分析了其应变率效应，为研究花岗岩的动态力学性能提供参考。

[1]冯明德，彭艳菊，刘永强,等.SHPB实验技术研究[J].地球物理学进展，2006，21(01)：273-278.

[2]Lindholm U S.Ye'arkly L M，Nagy A.The dynamic strength and fracture properties of dresser basalt[J].Int J Rock Mech Sci Geomech Abstr，1974，5(11)：181-191.

[3]于亚伦.用三轴SHPB装置研究岩石的动载特性[J].岩土工程学报，1992，14(03)：76-79.

[4]Verleysen P，Degrieck J，Taerwe L Experimental investigation of strain rate-dependent impact behavior of cementitious composites[J].Magaz Concr research，2002，54(04)：257-262.

[5]巫绪涛，胡时胜，孟益平.混凝土动态力学量的应变计直接测量法[J].实验力学，2004，19(03)：319-323.

[6]王永刚，施绍裘，王礼立.采用改进的SHPB方法对对泡沫铝动态力学性能的研究[J].实验力学，2003，18(02)：257-264.

[7]喻勇，张宗贤，俞海,等.岩石直接冲击破坏中的能量耗散及损伤特性[J].岩石力学与工程学报，1998，17(04)：386-392.

[8]戚承志，王明洋，钱七虎.弹粘塑忡孔隙介质在冲击载荷作用下的一种奉构关系——第二部分：弹黏塑性孔隙介质的畸变行为[J].岩石力学与工程学报，2003，22(11)：1763-1766.

[9]席道瑛.郑永来，张涛.大理岩和砂岩动态本构的试验研究[J].爆炸与冲击，1995，15(03)：259-266.

[10]Shan Y L，Jiang Y S，Li B Q.Obtaining dynamic complete stress-strain curves for rock using the split Hopkinson pressure bar technique [J].Int J Rock Mech Min Sci，2000，37(06)：983-992.

[11]刘剑飞，胡时胜，胡元育,等.花岗岩的动态压缩试验和力学性能试验[J].岩石力学与工程学报，2000，19(05)：618-621.

[12]谢和平，彭瑞东，鞠杨.岩石变形破坏过程中的能量耗散分析[J].岩石力学与工程学报，2004，23(21)：365-375.

[13]陶俊林.SHPB实验中几个问题的讨论[J].西南科技大学学报，2009，24(03):27-35.

[14]巫绪涛，杨伯源，李和平，等.大直径SHPB装置的数值模拟及实验误差分析[J].应用力学学报，2006，23(03)：431-435.

[15]翟越，马国伟，赵均海，等.花岗岩在单轴冲击压缩荷载下的动态断裂分析[J].岩土工程学报，2007，29(03):385-390.

[16]巫绪涛，代仁强，陈德兴，等.钢纤维混凝土动态劈裂试验的能量耗散分析[J].应用力学学报，2009，3，26(01)：151-154.

[17]杨圣奇，苏承东，明平美，等.岩石强度尺寸效应的研究方法和机理的研究[J].焦作工学院学报,2002，21(05)324-326.

[责任编辑：刘守义英文编辑：刘彦哲]

Strain Rate Effects on Shock Compression Based on SHPB

LI Dan,QI Wei-wei,WANG Yan-hua

(College of Civil & Environment Engineering，Anhui Xinhua University，Hefei，Anhui 230088，China)

ObjectiveGranite,as the important civil engineering material，has dynamic mechanical performance worth meaningful analysis，but the relevant researches are not sufficient.So the study of the dynamic mechanical properties of granite and analysis of strain rate effects of granite under shock compression on the dynamic mechanical properties provide reference for the dynamic study of granite.MethodsAfter selecting the appropriate size of the granite specimen,SHPB device was used to make impact compression experiments on granite specimen，obtaining more groups of curve of incidence wave，reflection wave and transmission wave under high strain rate.Then they were converted into the granite specimen stress，strain and strain rate of changing in time according to the theory of stress wave，obtaining the relationship curve between stress and strain，and dissipation energy in different strain rate.ResultsThe ultimate strength and peak strain of the granite specimen increased with the increase of strain rate but the amplification reduced，which showed that the granite ductility increased with the increase of strain rate.Dissipation energy and strain energy also increased accordingly with the increase of strain rate，and strain energy was always smaller than the dissipation energy but infinitely closed.ConclusionThe results of shock compression are markedly different from static compression about granite.The failure stress of granite specimens rapidly increases with the increase of strain rate.The peak stress,strain and dissipation energy increase with the increase of strain rate.Under the dynamic loads taking the dynamic performance of granite into consideration may make structural analysis more reliable in the actual engineering

granite;SHPB;strain rate;dissipation energy

国家自然科学基金项目(51309004)；安徽省高校自然科学研究项目(2008ZR019)；安徽省重点研究项目(kj2015A336)

李丹(1988-)，女，湖北黄冈人，安徽新华学院助教，硕士，主要从事结构力学研究。

O 442

A

10.3969/j.issn.1673-1492.2016.09.007