基于ANSYS的恒幅载荷下桥式起重机疲劳寿命模拟

周雨芬,周利东,朱 瑞,王 雷

(太原科技大学机械工程学院，太原 030024)



基于ANSYS的恒幅载荷下桥式起重机疲劳寿命模拟

周雨芬,周利东,朱 瑞,王 雷

(太原科技大学机械工程学院，太原 030024)

针对评估桥式起重机金属结构疲劳寿命的问题，以桥式起重机受力分析为基础，借助ANSYS软件的相互作用积分法，结合恒幅载荷下裂纹扩展寿命的理论，对箱型梁腹板跨中部位的腹板——下翼缘板处的裂纹进行分析，拟合出应力循环次数与裂纹尺寸的关系，得出恒幅载荷下桥式起重机的疲劳裂纹扩展寿命。同时，归纳桥式起重机疲劳寿命计算的影响因素及其试验推荐值。结果表明，循环次数与裂纹尺寸之间的关系符合疲劳裂纹扩展的客观规律。

ANSYS；桥式起重机；裂纹；恒幅载荷；疲劳寿命

在桥式起重机的使用过程中，疲劳与断裂是最常见的失效模式。准确预测疲劳寿命，对实现安全生产至关重要。如果使用寿命预测过短，可能会使起重机提前报废，造成资源浪费；使用寿命预测过长，可能会给企业与工人留下许多隐患，甚至带来灾难性的后果。

使用实验方法获得疲劳寿命的成本太大，因此越来越多的研究人员致力于使用软件模拟来得到近似于实际情况的结果，怎样使软件模拟得出的寿命更精确，是我们研究的重点。文献[1]将时间循环法与恒幅载荷疲劳裂纹扩展阶段的计算公式相结合，应用计算机模拟估算了桥门式起重机的疲劳裂纹扩展寿命；文献[2]通过ANSYS的二次开发模拟得到桥式起重机焊接箱形主梁的裂纹扩展路径；文献[3]应用ANSYS模拟得出了桥式起重机箱型梁疲劳裂纹产生的位置。

为了探索桥式起重机疲劳寿命预测评估方法，本文将ANSYS的相互作用积分法与恒幅载荷下疲劳裂纹扩展寿命数值计算方法相结合，对桥式起重机箱型梁跨中部位的腹板——下翼缘板处的裂纹的稳定扩展阶段进行分析，模拟得出恒幅载荷下桥式起重机的疲劳裂纹扩展寿命。为下一阶段，根据桥式起重机求受变幅载荷或随机载荷的疲劳裂纹扩展寿命提供了基础。

1 桥式起重机裂纹扩展机理

1.1 确定桥式起重机疲劳裂纹危险点的位置

对于桥式起重机最容易产生裂纹扩展的位置，从两方面来考虑。其一，由于桥式起重机是焊接结构，焊缝处最容易产生初始裂纹，如图(1)中的1号点,2号点和3号点处。其二，通过对桥式起重机的静力学分析可知，桥式起重机受随机载荷时，最大应力容易出现在跨中下翼缘板处受拉的部分。因此，在循环载荷作用下，桥式起重机金属结构计算关键的两个位置处于跨中，分别为：腹板——大隔板之间的焊缝处(1号点)和腹板——下翼缘板焊缝处(2号点)。

1.2 疲劳破坏机理

由于受到不同形式的载荷作用，金属结构中的裂纹形式通常可以简化为如下三种类型：I型(张开型)，II型(滑开型)，III型(撕开型)。根据桥式起重机的受力情况，通常为I型裂纹(张开型)。

图1 箱型梁容易产生裂纹的位置

裂纹的发展过程包括三个阶段：裂纹的萌生、裂纹的扩展和断裂。由于桥式起重机属于典型的焊

接结构，在焊缝部位，不可避免地会存在微裂纹、切口、咬边、夹渣等裂纹源，因此桥式起重机寿命评估时可以忽略裂纹的萌生阶段，只需要考虑后两个阶段即可。

疲劳裂纹扩展关心的是裂纹尖端附近的应力场，应力强度因子反映了裂纹尖端弹性应力场的强弱，其计算公式如下：

(1)

式中，f——几何修正系数；

σ——结构的应力；a——裂纹的尺寸。

疲劳裂纹扩展寿命与疲劳裂纹扩展速率相关，疲劳裂纹扩展速率可以用Paris公式来表示，如下式：

(2)

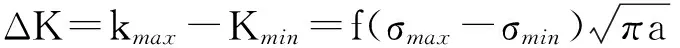
将(1)式代入(2)式，并积分得到金属结构在等幅载荷下的疲劳裂纹扩展寿命：

(3)

式中，a0——初始裂纹尺寸；ac——临界裂纹尺寸。

1.3 疲劳裂纹扩展寿命各参数

(1)几何修正系数f

它反映了构件和裂纹的几何尺寸对裂纹尖端应力场的影响[4]。通常，对于受拉伸的无限宽板中心裂纹，f=1；对于无限宽板单边裂纹，f=1.12.但是，在实际情况下，f随着板宽，裂纹长度等尺寸不断变化，不能单一的将它赋予某个值，它对计算结果影响很大。

(2)初始裂纹长度a0

桥式起重机属于焊接箱型梁，在使用初期就会由于焊接原因产生初始裂纹，用测量的方法能确定初始裂纹a0的尺寸，但是目前尚无统一标准对a0进行界定。

由文献[4]可知，a0对寿命计算结果的影响很大，因此严格控制a0的选取，对于提高评估疲劳裂纹扩展寿命的精度非常重要[4]。根据经验，桥式起重机的初始裂纹长度a0取值范围在0.5mm～2mm之间[5]。

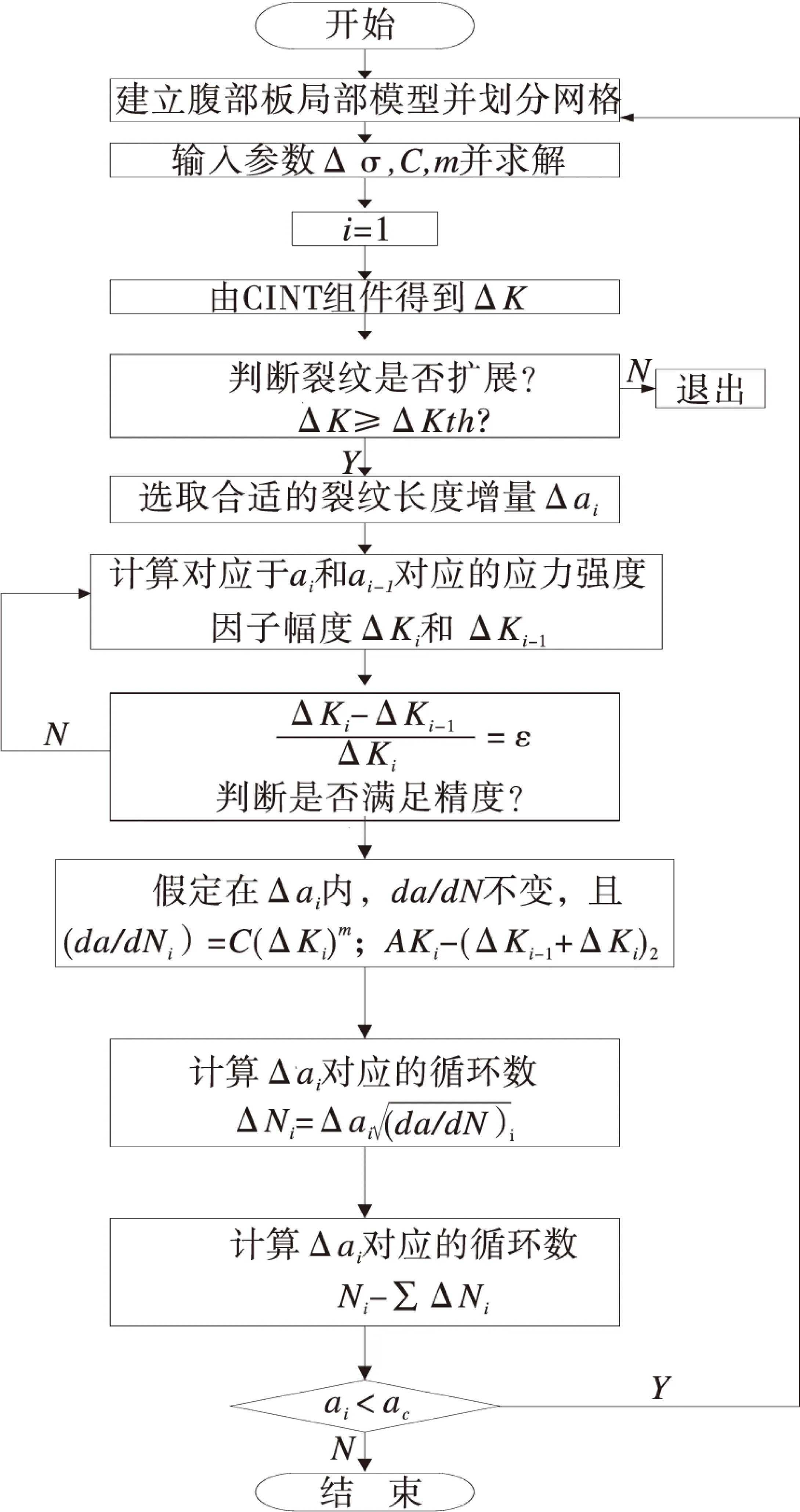
图2 恒幅载荷下裂纹扩展的数值计算流程图

注：CINT的内容将在第2部分详细叙述。

(3)临界裂纹长度ac

临界裂纹长度ac可以根据线弹性断裂判据得出，如下式：

(4)

式中，KC——材料的断裂韧性；σmax——最大循环应力。

临界裂纹对寿命的影响很小[4]，一般，可以选取结构的极限尺寸限制值，此处可以选取下翼缘板到中性层的距离。在ANSYS寿命求解过程中，选择边裂纹来建模，临界裂纹的求解公式中f取1.12.

(4)疲劳裂纹扩展速率参数C,m

Paris公式中的裂纹扩展参数C，m与材料属性、构件的几何形状有关[6],可以由疲劳裂纹扩展试验来确定。桥式起重机金属结构选用Q235，其参数可取C=2.61×10-13,m=3[5].

1.4 恒幅载荷下裂纹扩展的数值计算

对于恒幅载荷下桥式起重机跨中的腹板——下翼缘板焊缝处的裂纹寿命计算公式如下[7]：

(5)

式中，Wzx——桥式起重机箱型梁的中性层到下翼缘板的宽度；W——桥式起重机的腹板高度。

由于裂纹的尺寸a是不断变化的，f是关于a的函数，通常比较复杂，公式(5)不易积分，用数值积分的方法来计算，恒幅载荷下疲劳裂纹扩展的数值计算流程图如图2所示。

2 桥式起重机疲劳裂纹扩展的ANSYS建模与分析

应用ANSYS对恒幅载荷下桥式起重机疲劳裂纹扩展寿命预测的总体思路如下：

建立桥式起重机整机模型，并施加载荷进行分析求解。对桥式起重机跨中焊缝处已有初始裂纹的腹板建立子模型，并提取该子模型在整机相对应的力与约束，将其与恒幅载荷下疲劳裂纹扩展的数值模拟过程(图2)相结合，模拟恒幅载荷下桥式起重机的疲劳寿命。

2.1 桥式起重机模型的建立

由于桥式起重机主梁及端梁属于典型的薄壁箱型结构[8]，同时结合它的受力情况，选择shell63来建模[9],它的应力云图如图3所示。

图3 桥式起重机的von Mises stress图

从桥式起重机应力云图中可以看出，最容易产生裂纹的位置是腹板——下翼缘板焊缝处，在循环应力的作用下，裂纹沿着腹板金属材料向中性层延伸进行扩展，提取出此处的应力状态，将它作为下一步局部分析模型加载的输入参数。

2.2 基于ANSYS的应力强度因子计算

ANSYS12.0及以上版本增加了相互作用积分法，给桥式起重机金属结构疲劳裂纹寿命预测的研究提供了更大的平台。在应力强度因子计算方面，ANSYS软件提供了基于相互作用积分法的CINT组件，能得出疲劳裂纹的应力强度因子，并且具有很高的精度[10]。

其中：

CINT, TYPE, Par1

定义求解类型，CINT组件可以用来求解应力强度因子、J积分和能量释放率。

CINT, NCON, Par1

在裂纹尖端处定义计算所需要的围线数(如图6)，围线数越密集计算精度越高，越能满足计算要求。

2.3 裂纹分析模型的建立

根据桥式起重机跨中受力分析，选择跨中腹板局部400×200(单位：mm)进行建模，并且假定腹板——下翼缘板焊缝处的裂纹扩展方向与拉应力方向相垂直[11]。此处的初始裂纹a0使用全裂纹模型，通过关键点1-7-6-5-4和2-8-6-5-3建立两个面，如图4所示。

图4 初始裂纹模型

裂纹尖端附近采用奇异网格来划分，能实现应力场的奇异性。将裂纹尖端网格进行细化，其他部分使用常规网格，也可以缩短计算时间，如图5所示。应用KSCON命令，能够控制裂纹尖端的尺寸，将图5中的两个面中裂纹尖端的网格数各设置为20(周向)，裂纹尖端网格划分如图6所示。

图5 局部模型的网格划分图

图6 裂纹尖端的网格划分

3 算 例

某厂房使用的100 t/25 t的桥式起重机，跨度为19.5 m，起升高度为15 m，工作级别为A5.疲劳裂纹扩展速率参数为C=2.61×10-13,m=3.初始裂纹长度按照经验选取a0=0.5 mm，临界裂纹由公式(4)得出。桥式起重机所用钢材为Q235，该材料的弹性模量为2.05×105MPa，泊松比为0.3，密度为7 860 kg/m3，屈服极限为2.05×105MPa.

桥式起重机提取100 t的货物和空载时，跨中裂纹附近板的的应力幅为Δσ=101 MPa.将应力幅导入到局部分析模型，利用由图2流程图所编写的命令流进行计算。所得裂纹从a0到ac扩展的疲劳寿命循环次数为130 438次，裂纹长度与循环次数之间的关系图如图7所示。

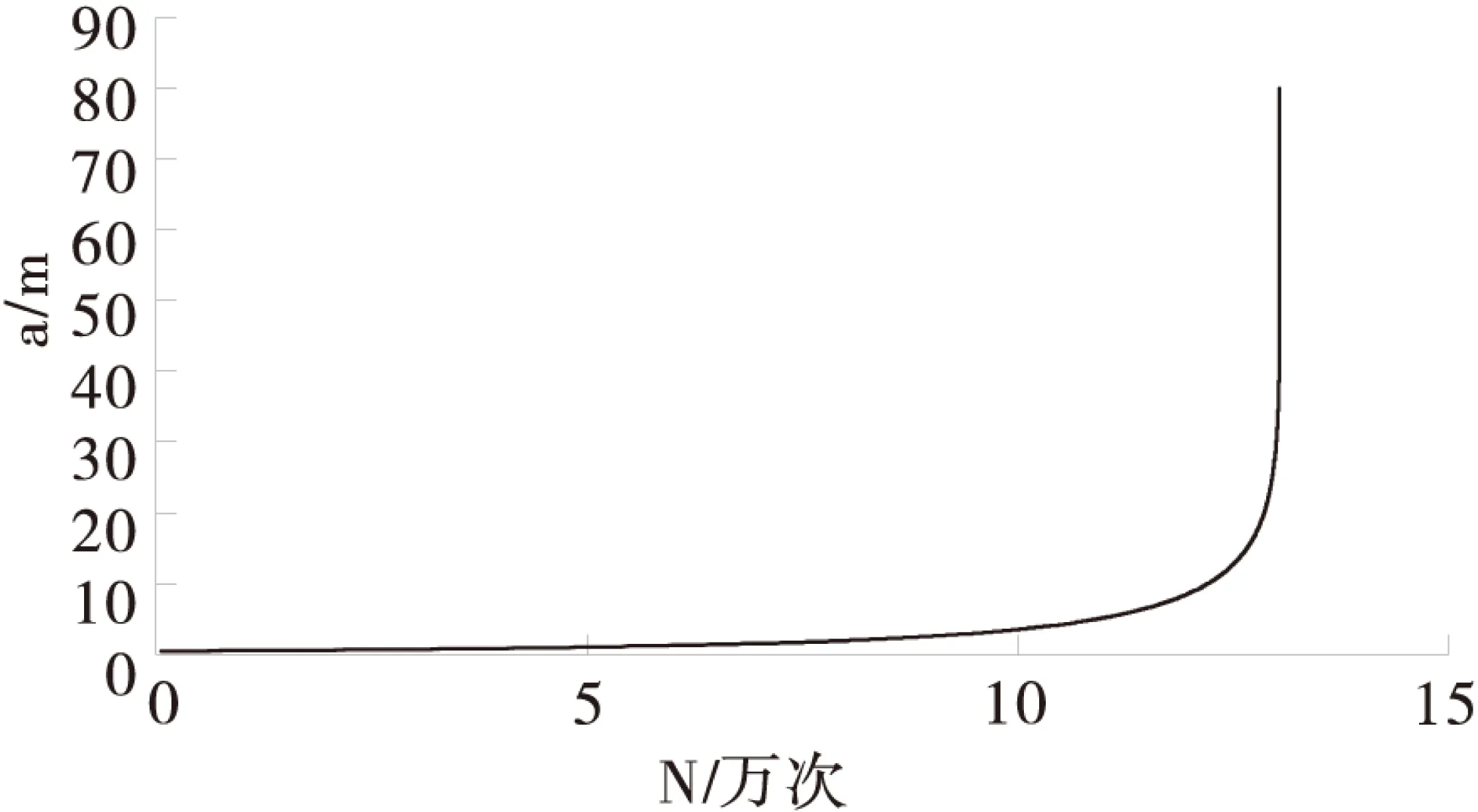
图7 裂纹长度与循环次数之间的关系

图7正确反映了在恒幅载荷下裂纹尺寸与循环次数之间的客观规律：刚开始裂纹增长比较缓慢，到后期裂纹增长速度加快。裂纹在20 mm后扩展速度加快，对于裂纹20 mm之后的使用阶段要重点关注并采取相应措施。

4 结 论

(1)对桥式起重机进行有限元分析，能快速地找出起重机疲劳最容易产生裂纹的位置及其应力，以及裂纹产生的原因。

(2)应用Paris公式计算了恒幅载荷下桥式起重机的疲劳裂纹扩展寿命，其中应力强度因子的计算采用了ANSYS中CINT组件的方法，能有效地提高计算精度，为重型机械疲劳剩余寿命的评估提出了一种新的方法。

[1] 程文明，王金诺.桥门式起重机疲劳裂纹扩展寿命的模拟估算[J].起重运输机械，2001(2)：1-4.

[2] 徐格宁，王建华.桥式起重机结构裂纹扩展路径模拟方法研究[J].安全与环境学报，2012(4)，207-211.

[3] 殷玉枫，曾光.基于Ansys的桥式起重机焊接箱形梁疲劳裂纹研究[J].起重运输机械，2012(11)：91-94.

[4] 陈传尧.疲劳与断裂[M].武汉:华中科技大学出版社，2002.

[5] 吴晓,罗薇，刘璐.在役桥(门)式起重机金属结构疲劳寿命预测分析[J].中国安全科学学报，2010(2)：95-100.

[6] RIGHINIOTIS, CHRYSSANTHOPOULOS. Probabilistic fatigue analysis under constant amplitude loading.[J].Journal of Constructional Steel Research,2003 (59) :867-886.

[7] 朱森第编，机械工程材料性能数据手册.北京：机械工业出版社，1994.

[8] 徐格宁.机械装备金属结构设计[M].北京：机械工业出版社，2009.

[9] 耿佳，张伟伟.移动载荷下桥梁速度响应小波分析多裂纹识别[J].太原科技大学学报，2014，35(1):71-76.

[10] 杨巍.基于有限元法对裂纹尖端应力强度因子的计算[J]. 沈阳航空航天大学学报，2014(3)：19-23.

[11] 翟甲昌.桥式起重机焊接向量的疲劳试验[J].起重运输机械，1994(2):3-8.

Simulation of Bridge Crane Fatigue Life Under Constant Amplitude Load Based on ANSYS

ZHOU Yu-fen, ZHOU Li-dong, ZHU Rui, WANG Lei

( Taiyuan University of Science and Technology, Taiyuan 030024, China)

Fatigue problem is one of the difficult evaluation problems of bridge crane steel structure. The life of crack on web-bottom flange of box beam was analyzed, which was based on the force bearing analysis on the bridge crane, with the help of the interaction integral method of ANSYS software and the theory of crack propagation life under constant amplitude loading. The relationship is fit from the stress cycles and crack, and the fatigue crack propagation life of bridge crane under constant amplitude loading was obtained. At the same time, the influent factors of bridge crane fatigue life calculation were summarized, and the value of the experience was recommended. It shows that the relationship between cycles and crack size accords with the objective law of fatigue crack propagation.

ANSYS， bridge crane， crack， constant amplitude load， fatigue life.

2015-10-27

国家自然科学基金资助项目(51275329); 太原科技大学博士启动基金(20122034)

周雨芬(1989-)，女，硕士研究生，主要研究方向为重大装备机械结构系统失效分析和安全评价。

1673-2057(2016)05-0395-05

TH215

A

10.3969/j.issn.1673-2057.2016.04.012