基于负荷介数和电气欧拉距离的电网关键环节辨识

江　浩，吕飞鹏，孔德洪

（四川大学电气信息学院，成都 610065）

基于负荷介数和电气欧拉距离的电网关键环节辨识

江浩，吕飞鹏，孔德洪

（四川大学电气信息学院，成都 610065）

为有效辨识电网关键环节，预防连锁故障，本文提出负荷介数和电气欧拉距离作为关键节点和线路的辨识依据。首先考虑电网中节点和线路的差异性提出负荷介数；然后结合线路介数和最大传输功率提出电气欧拉距离。该方法考虑线节点全局重要度、线路加权介数、线路度平均值以及最大传输功率对电网潮流分布的影响，将电网作为有向加权网络处理，计及电网节点度分布的差异性和线路功率传输约束，符合电力系统实际应用。通过IEEE 39节点系统的仿真计算和已有方法的对比，验证了本文所提方法的有效性。

关键环节辨识；线路加权介数；最大传输功率；负荷介数；电气欧拉距离

随着国民经济的飞速发展，电网建设也得到了持续的发展，不同区域电网之间的互联性变得越来越紧密。然而，近年来国内外不断发生的大规模停电事故，也给电力工作者们敲响了警钟［1-3］。如同2003年美加大停电一样，电网连锁故障通常是由某条线路开始，进而少数线路发生相继开断，最终蔓延至整个电网并导致系统崩溃。在事故蔓延扩大阶段电网的关键环节起着非常重要的作用，快速准确辨识出这些关键环节对预防电网连锁故障以及维持电力系统的稳定性都有着重要的意义。

目前，国内外对电网关键线路和节点的评估都进行了广泛而深入的研究，其中基于复杂网络理论的各种方法已经成为了研究热点［4-7］。文献［4］提出线路电气介数的概念，克服了加权介数模型假设母线间功率只按最短路径流动的弊端，但忽略了节点在电网中的重要作用；文献［5］采用一种基于系统潮流的介数值来辨识网络中的脆弱线路，通过对测试系统不同形式的攻击，验证了网络的脆弱线路，但同样没有考虑节点的作用；文献［6］仅从系统状态角度，研究了脆弱线路的辨识方法，忽视了节点和线路的结构脆弱性；文献［7］从网络的结构性视角出发，通过对网络最大流和电网有向加权拓扑模型的深度挖掘，建立传输贡献度指标来辨识电网的关键环节。

上述模型和方法都是基于复杂网络理论来研究电网的相关特性，它们大多仅考虑网络结构中节点或线路的单一作用。针对上述文献在建立相关指标辨识网络结构特征时存在的诸多不足，本文综合节点和线路的差异性并且考虑电网中节点加权介数指标，定义负荷介数对电网中关键节点进行识别；在辨识电网关键线路时，突破了以往仅考虑线路单一参数的不足，借用复杂网络中加权介数、节点度以及图论中最大流的概念，提出线路加权介数、线路度平均值和线路最大有功传输容量，进一步结合欧拉公式定义线路欧拉距离并将其作为线路重要性辨识的依据。通过IEEE 39节点系统关键节点和线路的辨识，验证了所提指标、方法的有效性和实用性。

1　基于复杂网络理论的负荷介数

1.1节点加权介数

介数是网络拓扑特性中一个很重要的指标，一个节点的介数衡量了通过网络中该节点的最短路径的数目。电网是一个能量承载网络，它将电能从各个电源点输送到负荷点。电网中一个节点介数越大，表明该节点传输的电能就越多，其地位就越重要。节点的介数最初是应用在社会网络中量化个体的重要性的，更准确地说节点的介数有时也指负载［8］。本文定义节点加权介数为

式中：njk为连接节点j和k的最小阻抗和路径的数量；njk（i）为连接节点j和k且经过节点i最小阻抗和路径的数量。

1.2考虑节点和边差异性的节点重要度

任何网络都是由节点和边所构成的，电网也不例外。复杂网络中节点的度是一个很重要的参数，节点度的大小反映了它与相邻节点联系的紧密性。考虑节点i在网络中地位的独特性，选用节点度分布概率P（ki）来考量节点重要度之间的差异性［9］，定义节点i的差异性Si为

式中：ki为节点i的度；N为网络的节点数；P（ki）为节点度值为k的概率。

网络中任意一条边所连接的节点的度值应该服从kiP（ki），即一个度值为k的节点被选中的概率应为度值为1的节点的k倍［10］，同时考虑节点i所在邻域内的关联性，选取节点i邻域的线路权值和和ki作为网络的基，定义与节点i相关的线路的差异性Di为

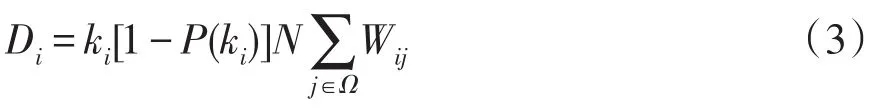
式中，Ω为与节点i有线路连接的节点集合。

综合考虑节点和线路在网络结构中的差异性，定义中间量I′i和节点重要度Ii分别为

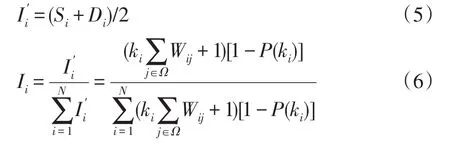
1.3负荷介数

在节点加权介数Bi和节点结构重要性Ii的基础上，给出关于节点i的全局关键性指标负荷介数的定义，即

式（7）表达的含义如下：

（2）从负荷介数指标的定义可以看出，如果节点i的度值k的出现概率P（ki）越小，那么网络中与节点i地位相当的节点越少，其重要性也相对更高；在实际电网中，节点度值特别大的节点数量占总节点数的比例非常小，即度值大的节点出现的概率就会特别小，然而这小部分节点往往是承担电能输送的关键节点，也说明这类节点相对更重要；

（3）与所计算节点相关联的线路越多，即相邻线路的权值之和越大，则对应实际电网中该节点容量越大，输送的电能也越多，那么该节点在网络中的地位就越关键。

2　基于图论的电气欧拉距离

2.1网络最大流

许多系统包含了流量问题，例如控制系统的信息流、供水系统中的水流等，电力系统也不例外。网络最大流问题是网络最优化问题的一个分支，其目的是寻求一个给定容量来限制网络中从源点到汇点的最大传输容量。

给定一个有向图D=（N，A，C），其中N为节点集，A为有向弧（边）集，C为弧或边的权值。所谓网络上的流，是指定义在边（弧）集合上的一个函数f=｛fij｝，并称fij为弧（i，j）上的流量。

满足下列条件的流f称为可行流：

（1）容量限制条件：对每一弧（i，j）∈A，有0≤fij≤cij，cij为弧（i，j）的最大有功传输容量。

（2）平衡条件：对于中间点，流出量等于流入量，即对每个节点i（i≠s、t，其中s和t分别为源点和汇点）有

对于源点s，记为

对于汇点t，记为

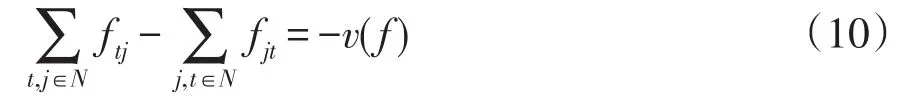
式中，v（f）为这个可行流的流量，满足流入节点的流量值之和等于流出节点的流量值之和。

可行流总是存在的。如令所有弧的流量fij=0，就可以得到一个可行流（称为零流），其流量v（f）=0。

2.2最大流及其计算

最大流问题就是求取一个流f，使其可行流的流量v（f）达到最大，并且满足

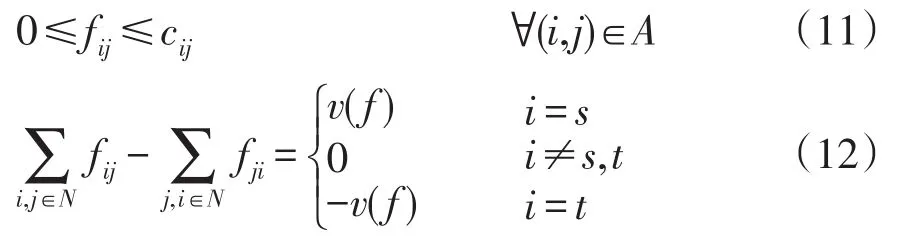
通过半个多世纪以来对最大流问题的研究，人们找到了多种算法来解决该问题，主要分为组合算法和线性规划算法。组合算法主要有Edmond-Karp增广路径法、Ford-fulkerson标号算法、Ahuja-Orlin的最短增广路径算法；线性规划算法主要有单纯形法、内点法等［11］。本文在使用Matlab软件计算电网线路最大传输功率时，采用效率更高的Edmond-Karp增广路径法编写程序。

2.3电气欧拉距离

前面已经给出节点加权介数的定义，考虑复杂网络中介数和度的重要性，类比于节点，提出线路加权介数bij和线路度平均值kij的概念。

线路加权介数bij定义为：通过线路（i，j）的顶点对的最小阻抗和路径数量。

线路度平均值kij定义为：线路（i，j）的两个顶点i和j的度值和的平均值，即（ki+kj）/2。

在电力系统中，线路的介数、度和最大有功传输容量这3个指标联系非常紧密。考虑线路加权介数bij、线路度平均值kij和线路最大有功传输容量cij对线路重要性的影响，采用欧拉距离公式，计算加权介数、度平均值、最大有功传输容量3个不同指标的综合作用，并以此定义线路的重要性指标，该指标记为

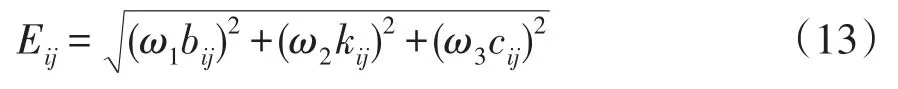
式中：Eij为线路电气欧拉距离；ω1、ω2、ω3分别为3个量的权重，且ω1+ω2+ω3=1，本文算例分析中取值为ω1=ω2=ω3=1/3。

需要说明的是式（13）中kij的值可能与bij和cij的数值上相差很大，为了消除式（13）中3个不同指标的量纲带来的影响，本文采用离差归一化方法对数据进行处理，可得

式中：y*为归一化后的数据；y为原数据；ymax和ymin分别为数据中的最大值和最小值。

计算时需对式（13）中的3个指标均进行归一化处理。

3　电力系统关键环节辨识流程

电力系统关键节点和线路辨识流程，分别如图1和图2所示。

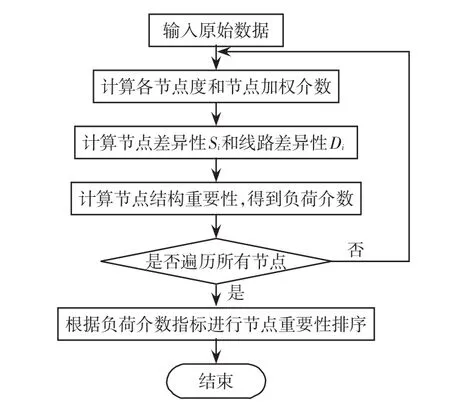
图1　关键节点辨识流程Fig.1　Flow chart of critical node identification

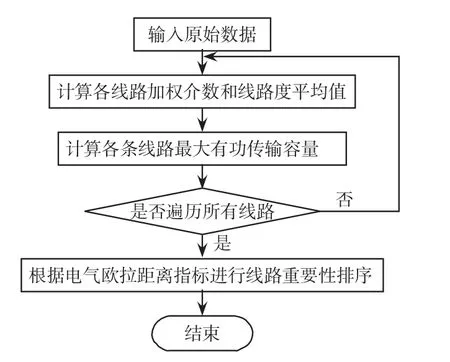
图2　关键线路辨识流程Fig.2　Flow chart of critical line identification

4　算例分析

本文采用IEEE 39节点测试系统对提出的算法进行仿真验证，系统的拓扑结构如图3所示。该系统共有39个节点、10台发电机和46条线路。

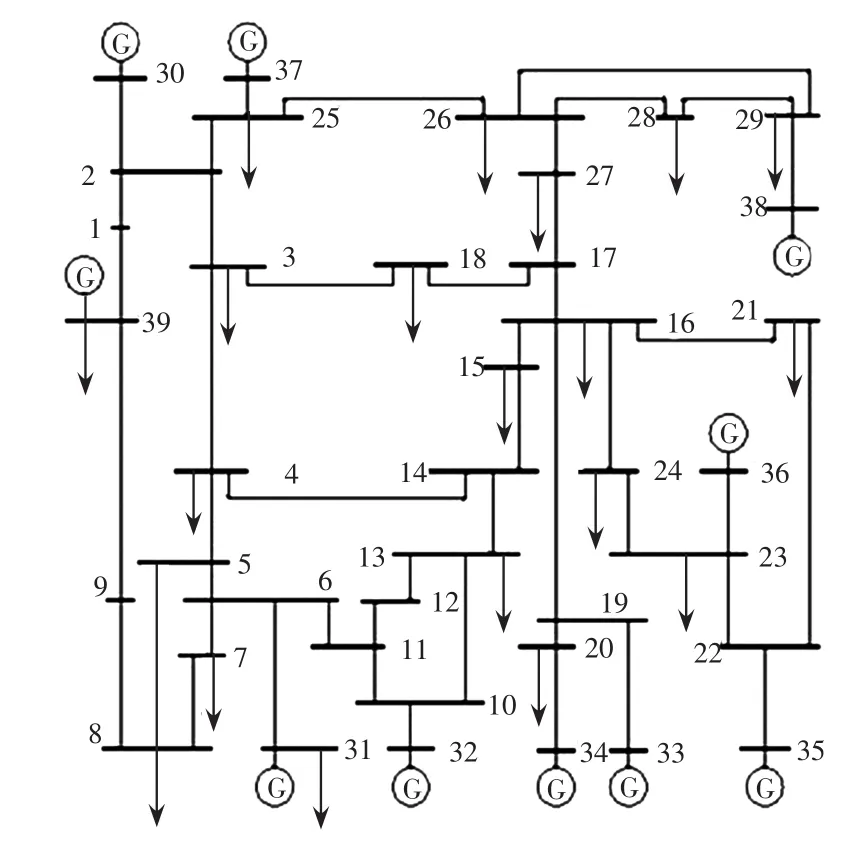
图3　IEEE 39节点系统Fig.3　IEEE 39-bus system

4.1关键节点辨识结果

根据第1.3节提出的指标和方法进行计算，对辨识结果进行排序并与其他方法进行对比，将所得数据分别列于表1和表2。

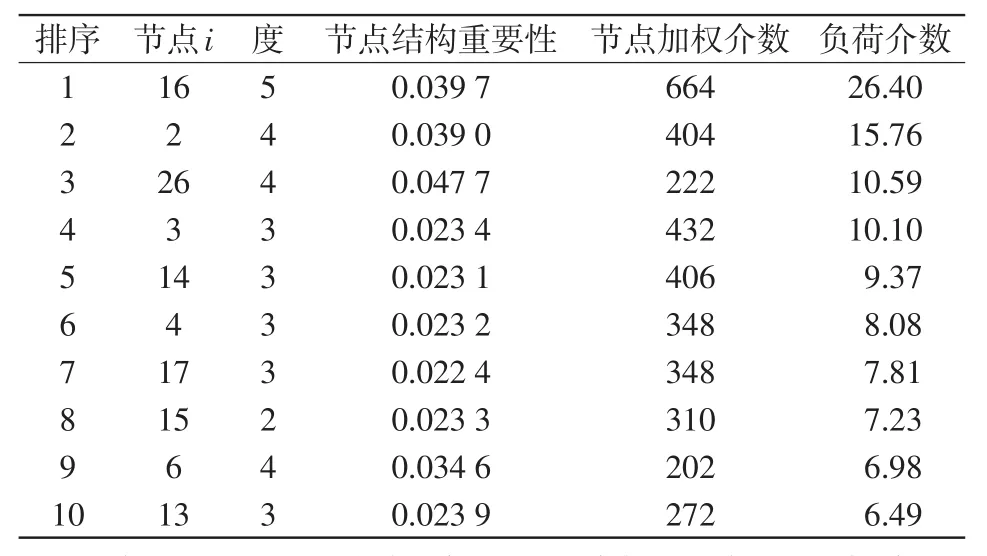
表1　关键节点辨识结果排序Tab.1　Rank of identification results of critical nodes

表1列出了排名前10的关键节点，从表中可知，节点结构重要性绝对值很小，使得不同节点间的结构重要性区分度低，例如节点16和节点2，以及节点3、节点14和节点4，它们在数值上都很小而且非常接近。相比之下，节点的加权介数在数值上较大，介数的放大效应使得不同节点的负荷介数在数值上的区分度比较大，辨识的精度和效果也比单独使用某一个指标要好。另外，负荷介数是将度关于节点和线路的差异性，以及节点的全局拓扑重要性加以全部考虑的综合性指标，故基于该指标辨识出的关键节点也更具全面性。

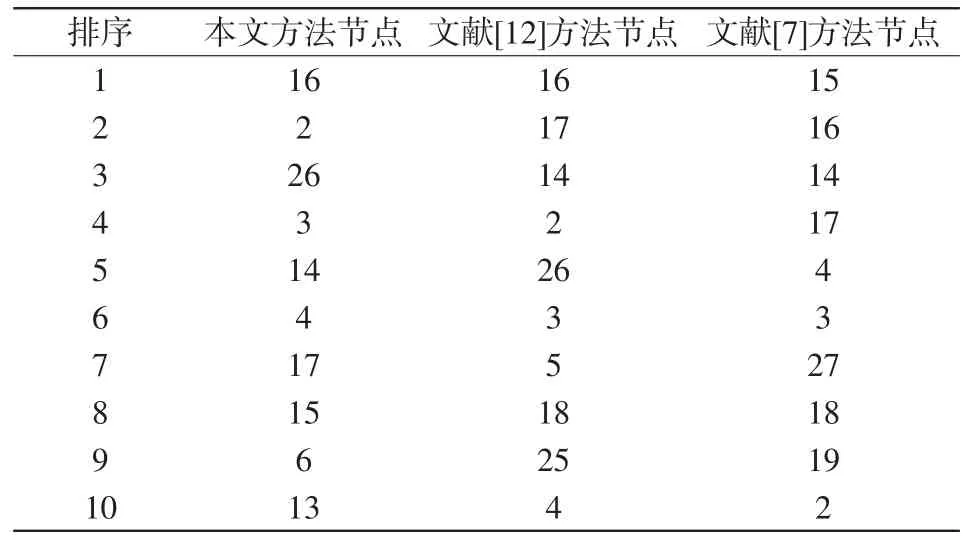
表2　不同方法关键节点辨识结果对比Tab.2　Comparison of identification results among critical nodes by different methods

表2中将本文辨识结果与文献［12］方法和文献［7］方法进行比较。本文方法与用节点收缩后的网络凝聚度计算得出的节点重要度排序的方法［12］有近似的排列和分布趋势，而与利用线路传输贡献度指标得出的结果［7］相差很大。本文方法与文献［12］方法均考虑了节点度的重要性，但本文在评估节点关键性时更加关注节点结构重要性以及介数的影响。例如节点2，文献［7］的方法判断与节点2相连的线路对该节点活跃度平均贡献较小，因而判断其重要性较小，但从图3中可知，节点2在拓扑上处于全局关键位置，发电机30、37和39的部分功率都会经过该节点向外输送，同时从表1可知节点2的度值和加权介数极大，故判断为网络关键节点，文献［12］方法与本文方法有类似结论。

可见，本文方法不仅关注节点在电网中的拓扑位置，也更加注重节点在功率输送和传播中的作用。

4.2关键线路辨识结果

按照本文所提出的关键线路辨识指标，计算系统中所有线路的电气欧拉距离，结果如图4所示。

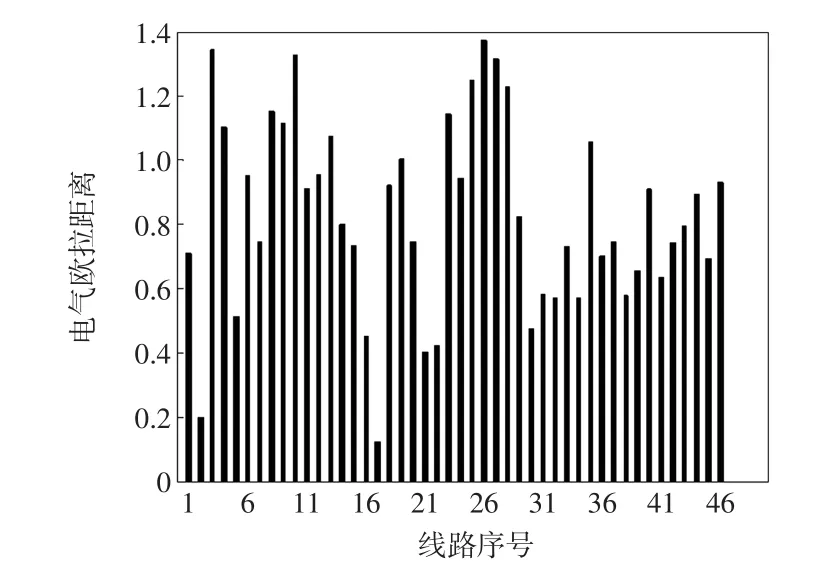
图4　IEEE 39节点系统关键线路识别Fig.4　Critical line identification in IEEE 39-bus system

按照本文所提方法挑选出关键性排在前10的线路，表3将线路重要性的最终排序与各线路的实际加权介数和最大传输功率作比较，其中所列电气欧拉距离是数据经归一化处理后求得的结果；表4把本文方法所得关键线路排序结果分别与用最大流作为指标的文献［7］中的方法和用加权介数作为指标的文献［13］中的方法做对比。

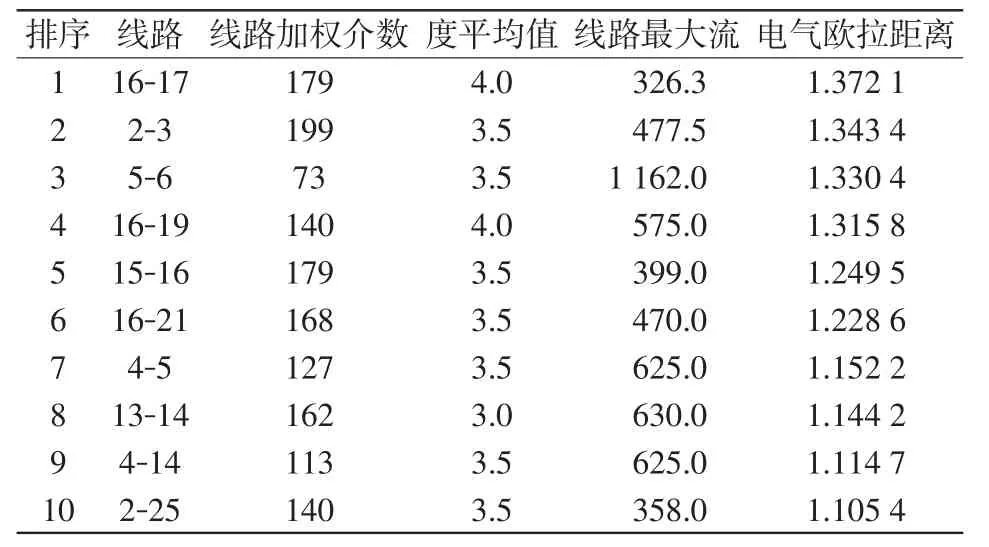
表3　关键线路辨识结果排序Tab.3　Rank of identification results of critical lines

表3中，将重要度排名前10的线路各自的加权介数和最大有功传输容量指标列出进行比较。从表中可见，网络最关键线路既不是加权介数最大的线路2-3，也不是有功传输容量最大的线路5-6，而是综合指标（电气欧拉距离）最大的线路16-17，同时关键性排在前10的线路度平均值均在3～4之间，这也验证了本文所提指标在考虑线路拓扑位置、全局重要性及线路对功率的传播和承载时的全面性。

进一步挖掘表中的信息，将线路16-17和线路15-16进行比较。在线路加权介数相同，线路15-16最大有功传输容量更大的情况下，线路15-16较16-17排名靠后。这是由于线路度平均值的影响，即线路拓扑位置重要性在线路关键性判别时的反映。同样的情况也适用于线路16-17和线路2-3的关键性比较，表3中还有诸多类似的情况，在此不一一列举。

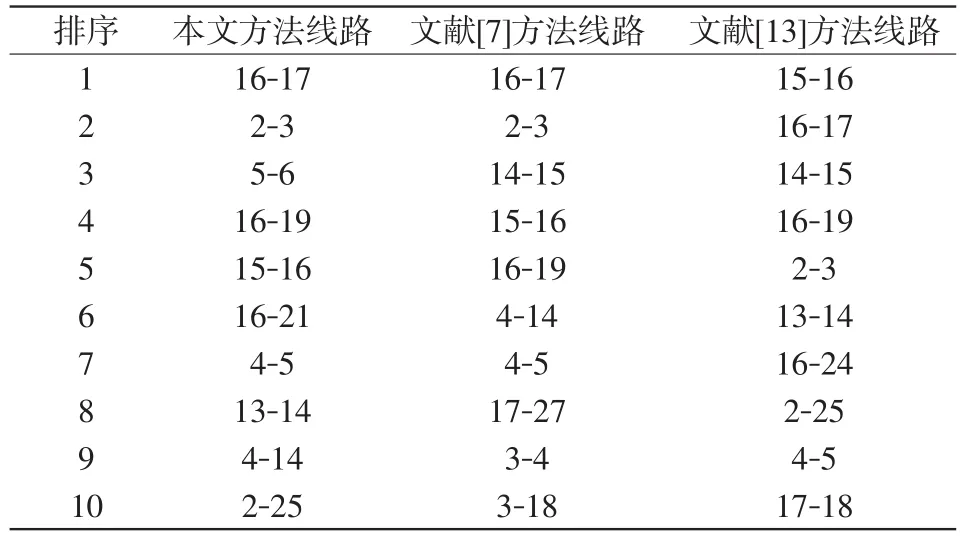
表4　不同方法关键线路辨识结果对比Tab.4　Comparison of identification results among critical lines by different methods

由表4可见，本文所提方法筛选出的关键线路与文献［7］方法和文献［13］方法所得重要线路排序总体分布趋势相近，与文献［7］方法关键度最大的前3条线路中的2条顺序相同，而本文所得到的关键性排序在前10位的线路中与其他两种方法均有6条相同，说明本文所提辨识指标的有效性。文献［7］和文献［13］辨识出的线路16-17、15-16和2-3均属于关键线路。从网络拓扑图来看，这几条线路均处于重要的输电通道上，虽然它们在电网中的功率传输量属于中等，其支路断开将会导致发电机30、33、34、35、36的功率无法送出，进而引发系统潮流的大范围转移，系统潮流均衡分布性严重降低。此外，线路16-19是33和34两台发电机向外输送功率的唯一通道，其断开对电力系统的稳定性影响巨大，甚至可能造成系统解列的严重后果。

通过与其他两种方法的横向对比和关键线路间的纵向对比，以及本文与其他两种方法在关键线路排序上的整体分布一致性，可知本文所提方法与其他两种方法虽然评估的角度不同，但辨识出的关键线路大多被另外两种方法的关键线路集所包含，验证了本文所提方法的有效性与合理性。

5　结语

本文在考虑关于度的节点和线路的差异性的基础上，提出通过负荷介数指标来辨识电力系统中的关键节点；在综合考虑线路在功率传输中的承担能力以及线路的局部和全局作用的基础上，提出利用电气欧拉距离指标对电力系统中的关键线路进行筛选。

通过对IEEE 39节点系统的仿真结果进行分析和对比，表明所辨识出的节点多处于网络的全局关键位置，且在功率输送和传播过程中有着重要的作用。辨识出的线路大多位于系统重要输电通道上，它们在系统中居于比较关键的地位。本文方法虽然具有一定的有效性，但未考虑扰动下电网的功率分布，进一步的研究工作将考虑二次设备的保护、暂态冲击引起的电压和功角变化特性等对关键节点和线路辨识的影响。

［1］胡学浩（Hu Xuehao）.美加联合电网大面积停电事故的反思和启示（Rethinking and enlightenment of large scope blackout in interconnected North American power grid）［J］.电网技术（Power System Technology），2003，27（9）：T2-T6.

［2］曾鸣，李红林，薛松，等（Zeng Ming，Li Honglin，Xue Song，et al）.系统安全背景下未来智能电网建设关键技术发展方向——印度大停电事故深层次原因分析及对中国电力工业的启示（Key technologies of future smart grid construction based on power system security：a view of blackout in India and experience and enlightment to power industry in China）［J］.中国电机工程学报（Proceedings of the CSEE），2012，32（25）：175-181.

［3］李博通，李永丽，姚创，等（Li Botong，Li Yongli，Yao Chuang，et al）.继电保护系统隐性故障研究综述（Overview of research on hidden failures in protection system）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），2014，26（7）：34-39.

［4］徐林，王秀丽，王锡凡（Xu Lin，Wang Xiuli，Wang Xifan）.电气介数及其在电力系统关键线路识别中的应用（Electric betweenness and its application in vulnerable line identification in power system）［J］.中国电机工程学报（Proceedings of the CSEE），2010，30（1）：33-39.

［5］刘耀年，术茜，康科飞，等（Liu Yaonian，Shu Qian，Kang Kefei，et al）.基于电抗加权介数指标的电网脆弱线路识别（Identification of vulnerable lines in power grid based on the weighted reactance betweenness index）［J］.电力系统保护与控制（Power System Protection and Control），2011，39（23）：89-92，100.

［6］孟绍良，吴军基，王虎（Meng Shaoliang，Wu Junji，Wang Hu）.电网脆弱性评价的灵敏度分析法（Power grid vulnerability assessment based on sensitivity analysis）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：89-93.

［7］鞠文云，李银红（JuWenyun，Li Yinhong）.基于最大流传输贡献度的电力网关键线路和节点辨识（Identification of critical lines and nodes in power grid based on maximum flow transmission contribution degree）［J］.电力系统自动化（Automation of Electric Power Systems），2012，36（9）：6-12.

［8］Watts D J，Storgatz S H.Collective dynamics of“smallword”networks［J］.Nature，1998，393（4）：440-442.

［9］蔡晔，曹一家，李勇，等（Cai Ye，Cao Yijia，Li Yong，et al）.考虑电压等级和运行状态的电网脆弱线路辨识（Identification of vulnerable lines in urban power grid based on voltage grade and running state）［J］.中国电机工程学报（Proceedings of the CSEE），2014，34（13）：2124-2131.

［10］Newman M E J，Park Juyong.Why social networks are different from other types of networks［J］.Physical Review E，2003，68（3）：361221-361228.

［11］吴艳，杨有龙，刘三阳（Wu Yan，Yang Youlong，Liu Sanyang）.基于网络流矩阵求解网络最大流（The network maximum flow based on the flow matrix）［J］.系统工程（Systems Engineering），2007，25（10）：122-125.

［12］刘艳，顾雪平（Liu Yan，Gu Xueping）.基于节点重要度评价的骨架网络重构（Node importance assessment based skeleton-network reconfiguration）［J］.中国电机工程学报（Proceedings of the CSEE），2007，27（10）：20-27.

［13］曹一家，陈晓刚，孙可（Cao Yijia，Chen Xiaogang，Sun Ke）.基于复杂网络理论的大型电力系统脆弱线路辨识（Identification of vulnerable lines in power grid based on complex network theory）［J］.电力自动化设备（Electric Power Automation Equipment），2006，26（12）：1-5，31.

Load Betweenness and Electric Euclidean Distance Based Identification of Critical Links in Power Grid

JIANG Hao，LYU Feipeng，KONG Dehong
（School of Electrical Engineering and Information，Sichuan University，Chengdu 610065，China）

To effectively identify the critical links in power grid and prevent cascading failures，load betweenness and electric Euclidean distance are proposed to identify the critical nodes and lines in power grid.Firstly，load betweenness is proposed by considering the distinction between nodes and lines.Then synthesizing the line betweenness and maximum transmission capability of lines，electric Euclidean distance is proposed.Considering the influence of global importance of nodes，and weighted betweenness，average degree and maximum transmission capability of lines on the power flow distribution，power grid is simplified as directed and weighted network with the constraints of node degree difference and power transmission，which is in accordance with the applications of power system.Simulation results on IEEE 39-bus system and comparison with other identification methods indicate the effectiveness of the model.

critical link identification；line weighted betweenness；maximum transmission capability；load betweenness；electric Euclidean distance

TM74

A

1003-8930（2016）10-0092-06

10.3969/j.issn.1003-8930.2016.10.016

2014-12-27；

2015-12-27

江浩（1990—），男，硕士研究生，研究方向为电力系统继电保护及电力系统状态评估。Email：781575041@qq.com

吕飞鹏（1968—），男，博士，教授，研究方向为电力系统继电保护和故障信息处理智能系统。Email：fp.lu@tom.com

孔德洪（1989—），男，硕士研究生，研究方向为电力系统继电保护与电力系统连锁故障。Email：504296972@qq.com