二氧化物气体在Cu-BTC中的分子筛效应理论计算*

翟尚宇，李维学，戴剑锋，王 青，陈立晶

(兰州理工大学 理学院， 兰州 730050)



二氧化物气体在Cu-BTC中的分子筛效应理论计算*

翟尚宇，李维学，戴剑锋，王 青，陈立晶

(兰州理工大学 理学院， 兰州 730050)

以构型导向Monte Carlo(CBMC)方法模拟了体系温度为298 K，气体压强为0.1～100 kPa下Cu-BTC对SO2、CO2、NO2吸附密度分布。并利用密度泛函理论(DFT)研究了Cu-BTC单元结构对客体分子(SO2、CO2、NO2)的吸附能。结果表明，Cu-BTC单元结构对SO2具有更高的吸附能。在比较了3种气体吸附过程后，进一步指出，在单一气体吸附与竞争吸附过程中，Cu-BTC对二氧化物气体粒子分子筛效应是其本身的结构能量差异以及客体分子能量差异综合作用的结果。

CBMC；DFT；Cu-BTC；SO2；分子筛效应；吸附

0 引 言

随着工业技术不断发展，煤炭燃烧向大气中释放了大量二氧化物气体，其中SO2与NO2可形成酸雨，CO2会造成温室效应，造成了大量环境危机与财产损失。减少该种气体在空气中的排放是解决环境问题的重要难题。

MOFs(metal organic frameworks)是由单元骨架结构所组装的多孔高分子材料，具有不饱和金属位和大的比表面积，在气体吸附与分离性能上具有很强优势。MOFs材料中Cu-BTC (Cu2+and benzene-1,3,5-tricarboxylate)具有独特四面体孔道结构[1]。近几年来，在理论方面出现了新的突破。Chen等[2]采用蒙特卡罗方法对Cu-BTC的甲烷吸附行为进行研究，为MOFs材料的模拟研究工作奠定了基础活性炭作为主要脱硫剂，其吸附行为研究已有大量成果[3]。对MOFs材料研究工作以吸附CO2以及烷烃气体居多[4]，为了改变以活性炭为主要脱硫剂的单一现状，利用高分离特性MOFs材料回收烟道气中SO2被越来越多科研工作者所尝试[5]。大多数学者将MOFs材料对客体分子的吸附作用研究重点放在对气体选择性吸附上[6]，而对MOFs材料所产生的分子筛效应形成机理很少深入探讨。将Monte Calo方法与密度泛函理论相结合来讨论Cu-BTC对特定氧化物气体所形成分子筛效应机理研究更是少见。

本文将Monte Calo方法与密度泛函理论相结合，通过对常温下二氧化物气体计算模拟，比较3种气体的吸附选择过程，最终以能量角度分析了Cu-BTC对二氧化物气体的分子筛效应的形成机理。本文结果将对以MOFs材料为脱硫剂的选型与性能评估提供更有力的理论支持。

1 模型构建与计算方法

1.1 模型构建

本文采用Chui等[7]所得的晶体数据构建Cu-BTC模型(如图1(a))。

图1 Cu-BTC晶体及孔道结构和Cu-BTC单元骨架结构

由图1(a)可知，以红色边框标识的是以Cu2-(COO)4为骨架的单元结构(如图1(b))。 单元结构尺寸为2.6343 nm，其中Cu原子之间距离为0.251 nm，具有D4h对称性，最终形成面心立方的四方形晶胞。图中还对Cu-BTC的不同孔道做了标识(如图1(a))，其中A为四面体孔道，B为主孔道。

1.2 计算方法

构型偏移蒙特卡罗(CBMC)[8]适合计算多孔复杂体系。本文利用CBMC方法，添加吸附粒子偏移概率，以提高多孔体系吸附精度。运算前，使用DMOL3模块对模型进行结构优化。设置平衡步数为2×105，生产步数为2×106，计算静电力相互作用时，采用Ewald与团簇相结合的方法，并以原子为基础计算范德瓦耳斯力。Ewald精度为0.001 kcal/mol，分子截断能半径为1.28 nm[9]。因Cu相关参数在Dreiding力场[10]中未给出，根据Chen等[2]的工作，在UFF力场[11]中选择Cu相关参数放入Dreiding力场，不同力场之间采用Jorgensen混合规则[20]。引用Chen等[2]对苯环的力场势能参数，如表1所示，以及Potoff等[12]、Sokolic等[13]、以及Bourasseau等[14]关于CO2、NO2、SO23种气体氧化物的力场参数(表2)，模拟二氧化物气体在Cu-BTC中吸附位与吸附能量分布。

表1 Cu-BTC骨架原子势能参数

注：a为取自Dreiding力场数据；b为取自UFF力场数据；c为取自陈丹等的工作。

表2 SO2、CO2、NO2 在Cu-BTC中各吸附位点结合能(eV)

密度泛函从头计算(DFT)适合于分析周期性大体系结构，本文通过DFT计算了Cu-BTC单元结构电荷密度。Cu-BTC单元结构因夹角不同对应两种孔道，夹角小的一侧(位点Ⅰ)对应四面体孔道，夹角大的一侧(位点Ⅱ)对应主孔道。为减小计算量并最大限度的考虑气体分子对骨架的综合作用，根据Chen等[15]对MOF-5的研究步骤，首先将Cu-BTC基本骨架单元取出(如图1)，并选取以Cu2+位为中心半径为0.5 nm的区间对称于单元骨架的两个位点，使S、C、N 3个中心原子所处坐标值相同，分别记为Ⅰ、Ⅱ。计算过程采用广义梯度近似(GGA)中PBE泛函，使用DFT-D色散校正方法计算范德瓦耳斯力，最大收敛循环步数为1 000步，收敛精度为1×10-6eV/atom，分子截断半径为0.5 nm。

为了很好与实验数据作对比，采用吸附量数据为过量吸附量。

(1)

式中，过量吸附量为nex，孔道内所有微观吸附质分子量均值nabs与气相分子量均值ng之差。

CBCM输入参量为逸度，因此压力与逸度转化采用P-R方程。

吸附能是表示吸附能力大小的物理量

(2)

式中，EB为吸附能，EMOF为MOF材料能量，EG为客体分子能量。

1.3 模型检验

本文引用Sun等[9]，温度为313K时，Cu-BTC对SO2、CO2及NO2等温吸附量模拟数据，以及Cavenati等[16]，温度为303K时，Cu-BTC对CO2等温吸附量实验数据(如图2所示)。本文等温吸附量数据与Sun等的模拟数据以及Cavenati等的实验数据均在误差范围之内，因此本文在计算中所采用的参数是可靠的。

2 结果与分析

2.1Cu-BTC对SO2、CO2、NO2的吸附位分析

为了更好地与两种状态下随气体压强增加至100kPa，吸附位三视组图(如图4所示)作对比，计算得到了298K下，3种气体单组分吸附曲线(如图3(a)所示)与气体组分为1∶1∶1的混合吸附曲线(如图3(b)所示)。

由图3(a)可知，在单体吸附过程中，SO2吸附量显著高于其它两种气体，从Potoff等[12]、Sokolic等[13]、Bourasseau等[14]对3种气体的力场参数工作以及Zhuo等[17]对MFI与CO2、N2的等温吸附曲线分析工作可知，SO2能够占据活性更高的吸附位(图4(a))。由NO2的低吸附量可知NO2吸附密度场游离在晶体表面，因此NO2与Cu-BTC结合力不高。吸附初期的CO2密度场首先集中在四面体孔道附近，可知CO2首先被Cu-BTC四面体孔道吸附，最终过饱和的CO2被挤出四面体孔道而进入主孔道。在竞争吸附状态下(图3(b))，SO2首先占据了高活性吸附位，吸附量最高(图4(b))。而NO2无法占据高活性吸附位。CO2在主孔道的竞争吸附中也处于劣势，两种气体在20kPa以后被挤出孔道之外。因此CO2与NO2在竞争吸附条件下吸附吸附量几乎为零。

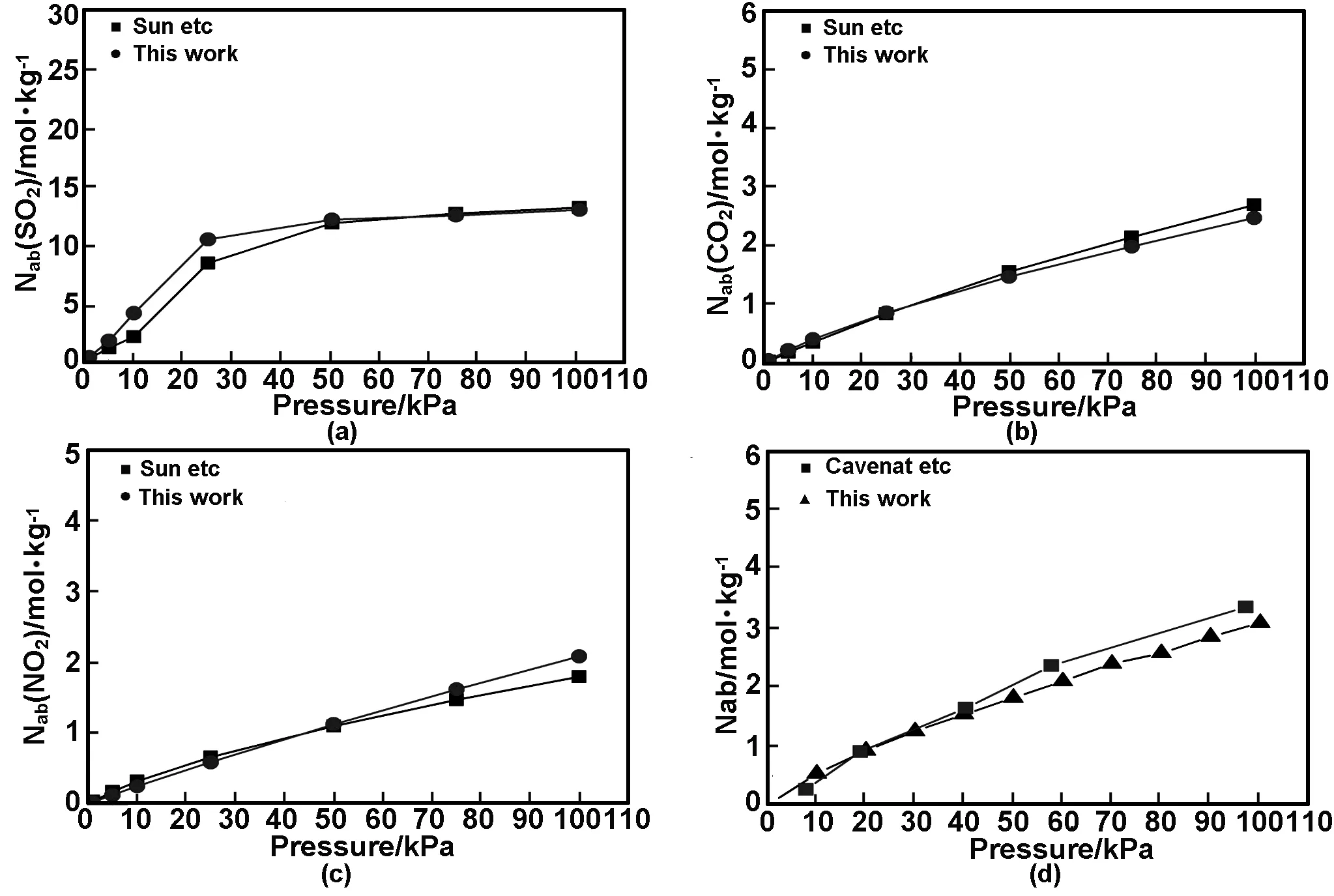
图2 Cu-BTC对SO2(a)、CO2(b)以及NO2(c)等温吸附曲线与模拟数据对比以及对CO2等温吸附曲线与实验数据对比(d)

图3 温度为298 K时Cu-BTC对CO2、NO2、SO2单组分与等比混合吸附曲线及吸附热曲线

2.2 Cu-BTC对SO2、CO2、NO2的吸附能分布

为了从能量角度解释3种气体整个吸附过程能量变化情况，利用CBMC方法，分别得到了常压下原胞内各气体在单组份与竞争状态下的吸附能分布比较图如图5所示。

通过图4与5可知，单体吸附与竞争吸附初始阶段，吸附能分布没有太大区别，随气体逸度不断增加，吸附能分布出现明显分化。

在单体吸附下，SO2吸附能最高。CO2形成了两种形式的峰值，左峰表现出较高极性，右峰极性较低。 NO2吸附能较小，大部分粒子吸附能分布显示出较小极性。

在竞争吸附下， SO2在Cu-BTC中具有比其它两种气体分子明显的优势。可以看出CO2在初始阶段仍然具有形成双峰趋势(20 kPa)，且吸附能明显小于SO2，最终由于SO2的排挤不再形成双峰。NO2的吸附能始终较低。结合图3(b)与图4(b)可以看出，最终仅有少量高吸附能的SO2与NO2粒子游离在晶体表面或者未被SO2占据的缝隙之中。

2.3 Cu-BTC对SO2、CO2、NO2的结合能与电荷密度分析

为了进一步解释在Monte Carlo计算过程中所出现的现象以及Cu-BTC两种孔道所产生的吸附差异，得到了3种气体在两种孔道结构附近的吸附能(表2)，以及Ⅰ、Ⅱ点位Cu-BTC骨架对SO2、CO2、 NO2电荷密度分布，在三维电荷密度场中选择场线范围最大的平面做切面，最终得到二维电荷密度图，如图6与7所示。

通过表2可知，SO2在两个位点吸附能差值绝对值较小，且能量值最高。说明SO2在Ⅰ、Ⅱ点位受到骨架夹角差异影响很小，与骨架具有较强的吸附作用，该客体分子吸附能与Binit等[18]计算水分子在Cu2+点位对骨架吸附能(40 kJ/mol)吻合较好。CO2在不同位点吸附能变化较大，因此CO2在结合能上受到单元骨架夹角差异影响较大，CO2在Ⅰ、Ⅱ点位的吸附能与Grajciar[19]等计算得到的在Cu-BTC中CO2在Cu2+附近吸附能(-0.3 eV)比较吻合。NO2在两个位点的吸附能差异并不明显，且绝对值较低。因此骨架结构差异性对NO2的影响不大，且相互作用较弱。吸附能计算数值均能很好呼应CBMC计算结果。通过单元骨架对两点位CO2的吸附能可知，在CBMC能量分布计算中(图5)，CO2左峰可认为是四面体孔道吸附能分布，右峰为主孔道。Ⅰ点位吸附能普遍高于Ⅱ点位，可知Cu-BTC内部存在能量差异，这与CBMC模拟工作中四面体孔道优先吸附客体分子而主孔道采取扩散吸附的结论吻合较好，并与Chen等[8]在其研究工作中提到烷烃在Cu-BTC内的吸附现象相符。

图4 温度为298k时CO2、NO2、SO2在单组分与等比混合条件下吸附位三视图

由图6与7可知， SO2、CO2、NO2场线数量相似，结合力场参数[12-14]中SO2、NO2、CO23种气体的中心粒子能量参数递减，以及表2计算数据可知， SO2与NO2同为三角形结构，吸附能大小取决于中心原子能量参数，能量参数越大与骨架的电荷等势面结合面积越大。CO2是直线型粒子，中心原子能量参数略小于NO2，然而CO2的特殊结构使其在相同情况下更容易接近Cu-BTC单元骨架，因此CO2会对单元骨架结构差异产生较大吸附能差异，在单元骨架夹角小的一侧吸附能高于NO2，夹角大的一侧低于NO2。同时，C能量参数远小于S，SO2比CO2中心粒子最低电荷密度场线更接近骨架中心粒子Cu+，即SO2中心粒子密度场范围大于CO2。3种气体分子在Ⅰ点位电荷密度场线与骨架的结合面积比Ⅱ点位更大，因此3种气体在单元结构差异情况下存在吸附差异，其中CO2差异最为明显。

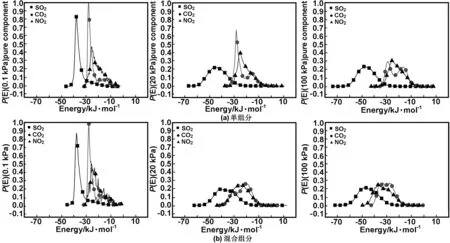
图5 温度为298 K时CO2、NO2、SO2单组分以及混合组分过程中吸附能分布对比图

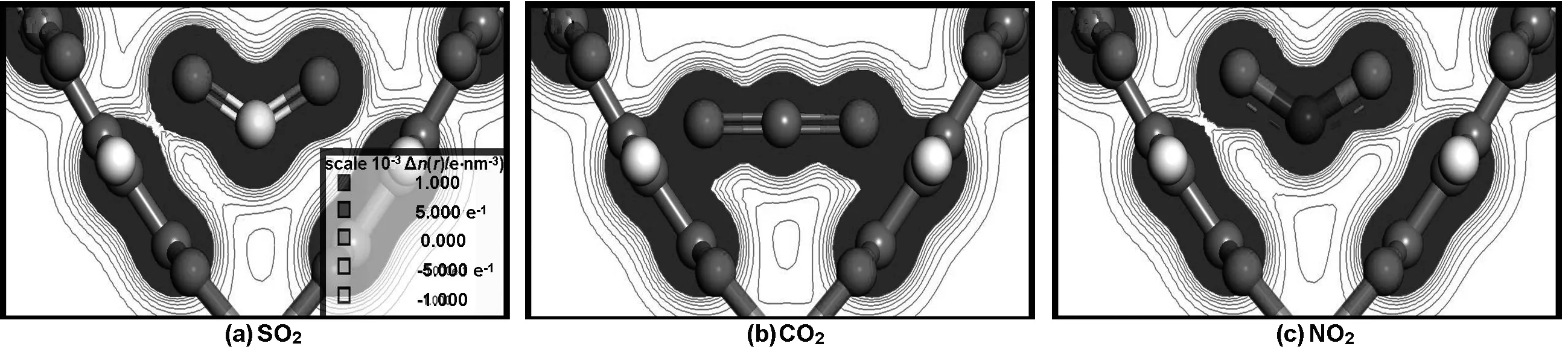
图6 Ⅰ点位Cu-BTC骨架对SO2、CO2、NO2电荷密度图

图7 Ⅱ点位Cu-BTC骨架对SO2、CO2、NO2电荷密度图

进一步指出，由于Cu-BTC四面体孔道的结构紧凑，且分支较多，所构成的吸附能阱较多，能够优先吸附客体分子。SO2与主孔道、四面体孔道的结合紧密，在整个吸附过程中吸附量平稳增长。CO2在骨架主副孔道吸附能差异较大，呈双峰态分布，在孔道大小允许情况下，孔道分支结构越多，结构越紧凑，吸附CO2的性能越好。NO2在主副孔道吸附状态并不活跃，Cu-BTC对NO2具有很好的过滤作用。

3 结 论

利用DFT/CBMC方法计算了Cu-BTC对CO2、NO2、SO2吸附位、吸附能分布以及骨架单元吸附能、电荷密度。结果表明，在二氧化物气体中，Cu-BTC对SO2分子筛效应是骨架材料本身的结构差异和客体分子结构与能量差异综合作用的结果。DFT/CBMC方法可以很好的解释Cu-BTC在气体吸附过程中所产生的结构与能量机理。

[1] Mileo P G M, Cavalcante Jr C L, Möllmer J, et al. Molecular simulation of natural gas storage in Cu-BTC metal-organic framework [J].Colloids Surf,2014,A 462:194-201.

[2] Chen Dan, Zhang Li, Liu Yingchun,et al. Adsorption and separation of Alkane Mixtures in Cu-BTC[J].Acta Chimica Sinica,2008,66:2227-2234

陈 丹,张 丽,刘迎春,等.烷烃混合物在Cu-BTC中的吸附与分离[J].化学学报,2008,66: 2227-2234.

[3] Huang G J. Thesis isothemal adsorption of sulfur dioxide on activated carbon[D].Changsha:Central South University,2013.

黄贵杰. 活性炭等温吸附SO2的研究[D].长沙:中南大学,2013.

[4] Paulo G MMileo,Célio L Cavalcante Jr, Jens Möllmer, et al. Molecular simulation of natural gas storage in Cu-BTC metal-organic framework[J].Colloids and Surfaces A:Physicochem Eng Aspects,2014,462:194-201.

[5] Song X D,Wang S,Hao C,et al. Investigation of SO2gas adsorption in metal-organic frameworks by molecular simulation[J].Inorg Chem Commun, 2014,46:277- 281.

[6] Wang Jiachen,Tong Minman,Shan Chao,et al. Molecular simulation of effects of impurities on flue gas separation in metal-organic erameworks[J]. Chem J Chinese Universities,2015,36:316-324.

王佳晨,童敏曼,单 超,等.杂质对金属-有机骨架材料分离烟道气性能影响的分子模拟研究[J].高等学校化学学报,2015,36:316-324.

[7] Chui S S Y,Lo S M F,Charmant J P H,et al. A chemically functionalizable nanoporous material [Cu3(TMA)2(H2O)3]n[J]. Science,1999,283:1148-1150.

[8] Frenkel D, Smit B. Understanding molecular simulation:from algorithms to applications[M].San Diego:Academic Press,2002.

[9] Sun Weizhen,Lin Lichang,Peng Xuan,et al. Computational screening of porous metal-organic frameworks and zeolites for the removal of SO2and NOxfrom flue gases[J]. AIChE J,2014,60:2314-2323.

[10] Stephen L,Mayo Barry D, Olafson, et al. Dreiding: a generic force field for molecular simulations[J]. J Phys Chem,1990,94:8897-8909.

[11] Rappé A K,Casewit C J,Colwell K S,et al. UFF a full periodic table force field for molecular mechanics and molecular dynamics simulations[J].W M J Am Chem Soc,1992,114:10024.

[12] Potoff J,Jeffrey J,Siepmann J. Vapor-liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen[J]. AIChE J,2001,47: 1676-1682.

[13] Sokolic F,Guissani Y,Guillot B.Molecular dynamics simulations of thermodynamic and structural properties of liquid SO2[J]. Mol Phys,1985, 56:239-253.

[14] Bourasseau E,Lachet V,Desbiens N,et al. Thermodynamic behavior of the CO2+NO2/N2O4mixture:a monte carlo simulation study[J]. J Phys Chem B,2008,112:15783-15792.

[15] Chen C,Pang J,Han S,et al.Influence of functional group decoration on gas adsorption in MOF-5[J]. Acta Phys Chim Sin,2012,28(1):189-194.

陈 驰,庞 军,韩 爽,等. 官能团修饰对MOF-5的气体分子吸附影响[J].物理化学学报,2012,28(1):189-194.

[16] Cavenati S,Grande C A,Rodrigues A E. Metal organic framework adsorbent for biogas upgrading[J].Ind Eng Chem Res,2008,47(16):6333-6335.

[17] Zhuo Shengchi. Computer simulation of capturing CO2by porous materials and self-assembling of surfactant[D].Shanghai: East China University of Science and Technology,2010.

卓胜池.介孔材料捕集CO2及表面活性剂自组装的模拟[D].上海:华东理工大学,2010.

[18] Binit Lukose,Barbara Supronowicz,Petko St Petkov, et al. Structure and electronic structure of metal-organic frameworks within the density-functional based tight-binding method[J]. Phys Status Solidi B,2012,249:335.

[19] Grajciar L,Wiersum D A,Llewellyn L P,et al.Understanding CO2adsorption in CuBTC MOF:comparing combined DFT-ab initio calculations with microcalorimetry experiments[J]. J Phys Chem C,2011,115(36):17925-17933.

[20] Jorgensen W L,Madura J D,Swenson C J.Optimized intermolecular potential functions for liquid hydrocarbons[J]. J Am Chem Soc,1984,106(22): 6638-6646.

The theoretical calculation of molecular sieving effect about dioxide gas in Cu-BTC

ZHAI Shangyu，LI Weixue，DAI Jianfeng，WANG Qing，CHEN Lijing

(School of Sciences, Lanzhou University of Technology, Lanzhou 730050, China)

Configurational-bias monte carlo (CBMC) techniques were combined to simulate the adsorption density field about SO2, CO2and NO2at 298 K, 0.1-100 kPa in copper (Ⅱ) benzene-1, 3, 5 tricarboxylate (Cu-BTC). Density funational theory (DFT) were combined to explain the adsorption energy of the Cu-BTC’s structure unit for guest molecules (SO2, CO2, NO2). The research result shows that the structure unit of Cu-BTC had higher adsorption energy for SO2. With the comparison on adsorption process of three kinds of gases, further noted that The obvious molecular sieving effect of Cu-BTC for dioxide gas with the process of pure component sorption and mixture component adsorption is caused by the binding energies’ difference of structure and guest molecules.

CBMC; DFT; Cu-BTC; SO2; molecular sieving effect; adsorption

1001-9731(2016)10-10107-06

国家自然科学基金资助项目(50873047);甘肃省科技计划资助项目(1010RJZA045)

2015-08-25

2015-11-25 通讯作者：李维学，E-mail: lwx@lut.cn

翟尚宇 (1990-)，男，兰州人，硕士，师承李维学教授，从事高分子团簇材料研究。

O631；O64

A

10.3969/j.issn.1001-9731.2016.10.019