基于扩展卡尔曼滤波算法的无人机定位*

杨润丰，骆春波，张智聪，李铭钊

基于扩展卡尔曼滤波算法的无人机定位*

杨润丰**1，骆春波2，张智聪3，李铭钊4

（1.东莞职业技术学院电子工程系，广东东莞523808；
2.英国埃克塞特大学数学与计算机科学系，英国埃克塞特EX4 4QF；3.东莞理工学院机械工程学院，广东东莞523808；4.中国电子信息产业集团有限公司，北京100846）

无人机的移动定位是应对无人机机动性和应用环境复杂性的关键技术。为解决无人机中的全球定位系统（GPS）信号失效问题，提出了一种通过机载无线射频的接收信号强度解决定位问题的技术，分别采用扩展卡尔曼滤波方法估计距离和最小二乘方法估计路径损耗因子两种处理方法。理论分析和实验测试结果证实所提算法对有色噪声干扰下的接收信号有较好的增强效果，基于80%的置信水平，新算法相对于白噪声模型将估算误差从9.5 m减少到了4 m，还进一步提供了融合惯性导航的算法。

无人机；移动定位；扩展卡尔曼滤波；距离估算

1 引 言

无人机在野外搜救应用中，需要进行信息采集、数据融合等移动通信任务[1-3]，准确快速的移动定位是完成这些任务的保障。因此，移动定位是应对无人机机动性、灵活性及其应用环境复杂性的关键技术。现有的无人机定位技术主要基于全球定位系统（Global Positioning SYstem，GPS），但是当卫星遭遇传输信道受阻、天气条件干扰等因素影响的时候，GPS信号将变微弱甚至失效，因此不能保证无人机GPS信号的正常接收，这给无人机的控制带来难以预测的困难，甚至给无人机带来危险。现有的其他技术包括利用无线射频信号的到达时间或到达时差[4]、到达角[5]、接收信号强度[6]等方法实现距离的测量和定位。前两个方法需要高度精确的设备或者天线阵列和复杂信号处理模块的支持，增加了无人机平台的负载、复杂性和成本。目前，国际上研究提出了基于接收信号强度的定位方法，并证明了其是一个更为方便和经济的解决方案。

无人机定位研究是当前国内外研究的一个热点问题[7-8]，例如，基于接收信号强度的定位技术，虽然具有算法简单等特点，但是它的一个突出问题是当无线信号受到噪音和干扰的影响时，信号强度的测量值比较复杂且无规则。本文所提定位采用了最小二乘法来处理，然而，最小二乘法在白噪声影响下所测的定位结果较准确的优势受到了一定的限制[9]。由于无人机飞行姿态的多样性、环境的复杂性以及信号传输会受环境影响等，使用最小二乘法会产生大比例的误差。为了提高基于接收信号强度算法定位的精确度，本文进一步提出扩展卡尔曼滤波的处理方法，并在有色噪声传输模型中进行了测试和分析。此外，影响算法精度的另一个因素是传播路径损耗因子。因为在无线信道中路径损耗因子并不是常量，本文还提出在无人机飞行应用中实时估算路径损耗因子的自适应算法，从而提高了移动定位的精确度，更好地保证了无人机群的控制，相对于已有的算法[7，10]，本算法具有更高的精度和适应性。

为了方便理论分析，文中相关的符号表示如下：T表示矩阵转置，lg表示以10为底的对数函数，min{•}和max{•}分别表示选择输入参数的最小值和最大值，║•║表示欧几里得范数，δ（•）表示狄拉克冲激函数，E{•}表示矩阵期望值。

2 系统模型

2.1 系统模型

确定一个物体的位置通常需要3个以上已知自身位置信息的参考节点。如图1所示，共有J个已知位置信息的参考节点，标记为Rj（j＝1，2，…，J），共有I台需定位的无人机，标记为Ui（i＝1，2，…，I）。这些参考节点可以是其他无人机、基站或接入点等，它们能够获取自己的准确位置信息和时钟同步的校准信息。每一台需定位的无人机使用无线射频信号按时间戳广播一个预定义的控制消息，这些信息经过信道时，可能遭受衰减、干扰和其他噪音的影响。

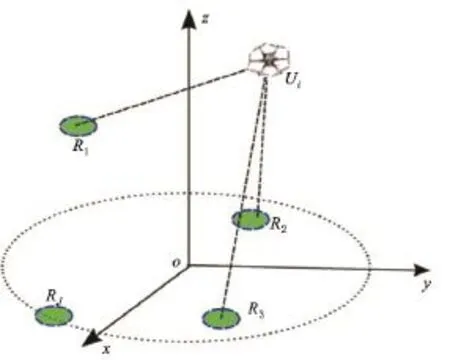
图1 无人机位置估算模型Fig.1 UAVs Position estimation model

采用这一模型的关键是使用机载无线射频通信模块的接收信号强度估算无人机和参考节点之间的距离。无人机组以刚体组合形式建模，它们的位置信息和参考节点位置可分别由式（1）和式（2）表示：

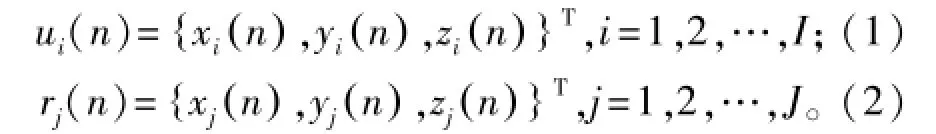
式中：n表示时间戳。

在图1模型中，可根据3个参考节点的距离信息估算一台无人机的位置。例如，无人机Ui的位置可表示为

2.2 信道模型

电磁波在无线电信道传播中常遭受噪声等各种因素干扰影响，而且发射端和接收端的移动也会带来多普勒效应和不稳定状况。因此，在信道建模中，引入自适应参数估算算法以应对物理环境变化的复杂无线信道。信道模型[8]表示为

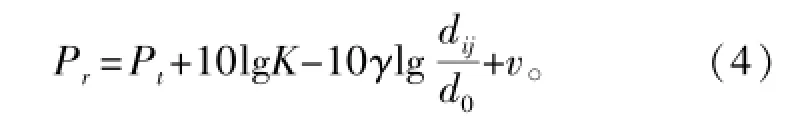
式中：Pr和Pt分别是接收功率和发射功率，单位是dBm；K是常数，其值取决于与d0测量值相关的平均信道衰减和天线特性；dij是无人机Ui与参考点Rj的距离；γ是路径损耗因子；υ是以dBm为单位的噪声功率。

设d0＝1 m，以时间戳表示路径损耗模型，如公式（5）所示：

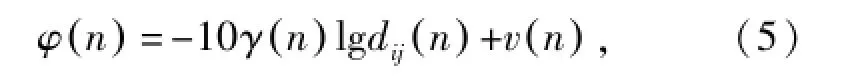
并用其测量距离。通常公式（5）中的噪声可采用高斯分布建模，但有色噪声在实际环境中对无人机无线通信影响极大。

3 基于色噪声建模的算法设计

3.1 噪声分析

通过应用阿伦方差的群集分析工具对一段无人机的接收射频信号进行统计分析发现，除了白噪声外，无线电信号也受有色噪声的影响（如图2所示），因此需要进行更准确的噪声建模。

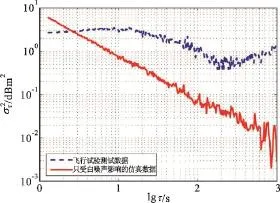
图2 无人机接收信号的阿伦方差Fig.2 The Allan variance of the received radio signal for a UAV

假设收集了N个数据φ（n），n＝1，2，…，N，把这些数据分组成M＝N/f个集群，然后利用公式（6）计算阿伦方差：

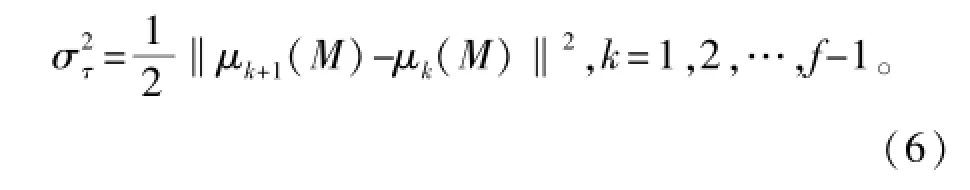
式中：τ为关联时间和f为采样频率；μk（M）＝

图2反映了无线接收信号的阿伦方差情况，从双对数谱的斜率可以看出，因为仿真数据添加了人为的白噪音，其斜率是-1，而此时（lgτ＜1）真实数据因为受有色噪声的严重影响，其斜率的变化较大，特别是在图中右端，竟呈现正数斜率。

随着频率f的增大，阿伦方差平方的误差减少，其置信区间如公式（7）所示：

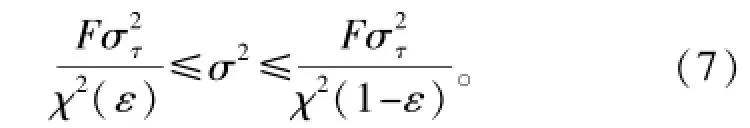
式中：σ2是真实方差值；F是估算量自由度；χ2是卡方分布的累积分布函数；ε是接近0的非负数。

3.2 有色噪声建模

根据以上相关噪声的观察分析可以看到，加性高斯白噪声和色噪声的建模区别主要在于普通噪声在频谱范围内具有常数值的功率密度，而色噪声在不同的频段上具有不同的功率谱密度。在时域来看，白噪声在相关图像上具有接近直线的下降趋势，而色噪声的曲线比较复杂，通过估计色噪声的阿伦方差曲线，可以获得对色噪声的近似模拟，即应用高斯马尔可夫过程建立一个连续时间自回归模型[11]：

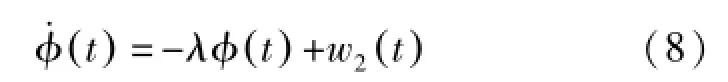
式中：λ是高斯马尔可夫过程系数，它描述了色噪声在不同相关时间内的特征，对于色噪声的建模和处理非常重要，后文将详细介绍它在卡尔曼滤波器中的应用；W是加性白噪声W2（t-T）]＝δ（T）。

把公式（8）转换为离散时间域表示：

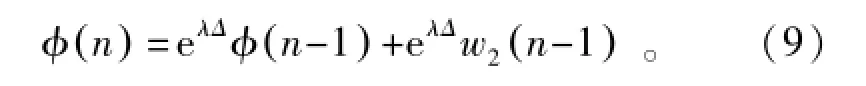
式中：Δ为时间增量。

由于激励噪声W2（n）的影响，在不失一般性的情况下，设n≥m，噪声φ（m）和φ（n）的关联可表达为

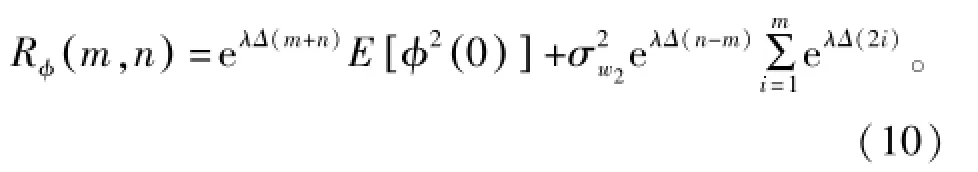
为了保持模型的收敛性，公式（10）中λ必须小于0。当m和n的值足够大时，式中第一项为0。第二项需要展开，把求和项进行求和运算，求和的结果是，进而简化得

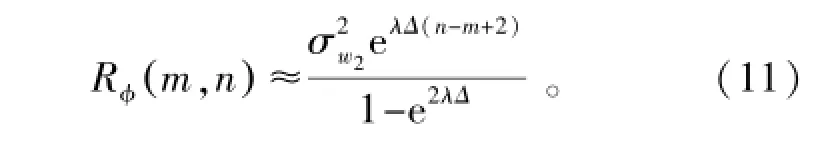
3.3 位置估算

应用扩展卡尔曼滤波方法实现距离估算。首先，根据以上信道和噪声的分析，结合公式（3），无人机Ui与参考点Rj的距离可建模型为

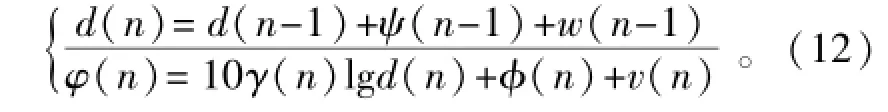
式中：ψ（n-1）是可选的控制输入，如惯性测量；W（n-1）是噪声估算，常可看作为高斯分布N（0，δ2）；φ（n）是有色噪声测量值；υ（n）是含方差R的白噪声测量值；设初始条件为n＝0时，d（0）＝d0和ψ（0）＝0。

公式（12）的第一个方程表示状态，第二个方程是测量方程。结合公式（8），有色噪声状态可表达为

式中：W2（n-1）是公式（7）中带方差的白噪声。

利用公式（14）可把公式（12）的第一个方程与有色噪声状态方程（13）合并：

式中：c（n-1）＝[d（n-1），φ（n-1）]T，ψ（n-1）＝[ψ（n-1），0]T，并且W（n-1）＝[W（n-1），W2（n-1）]T。噪声处理矩阵为Q＝E{WWH}，f（•）的雅可比矩阵可计算为

对卡尔曼滤波器的测量方程为

式中：h（c（n））＝10γ（n）lgc1（n）＋φ（n），并结合其偏导矩阵（雅可比矩阵）

由公式（14）和（16）推导得卡尔曼滤波算法的预测状态向量为

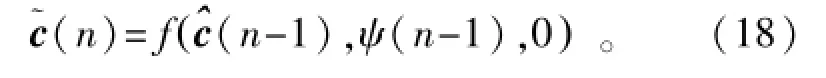
对先验估计误差协方差的计算：

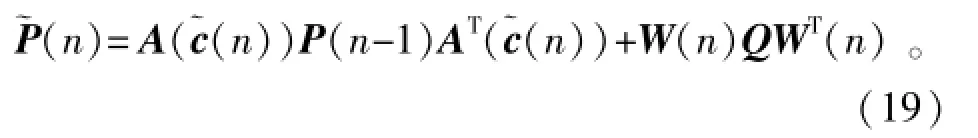
式中：P（n-1）是后验误差协方差估计，通常初始条件设P（0）＝1。

误差协方差受测量信号的影响可表示为

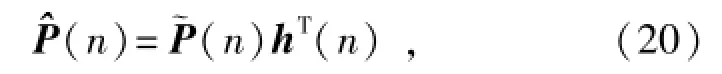
那么，卡尔曼增益可更新为

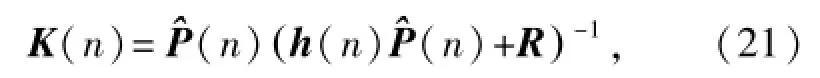
预测状态估计可更新得

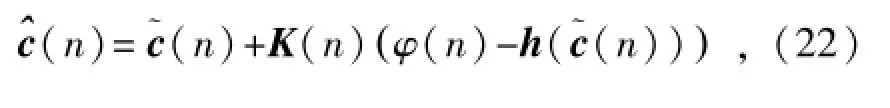
最终，后验误差协方差估计更新为

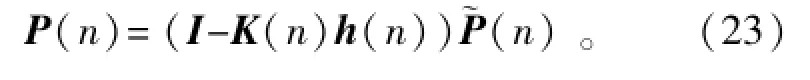
4 路径损耗因子自适应估计算法的增强方案

随着无人机的移动，其运行的物理环境不断变化，在无线通信模型中采用固定的路径损耗因子显然是不现实的，我们应用改进最小二乘法对路径损耗因子的估算，路径损耗模型（5）可表示为

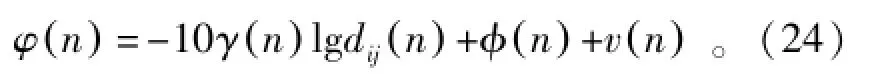
式中：f（γ（n））＝-10γ（n）lgdij（n），并设已有M个测量数据包括dij，误差函数可写成

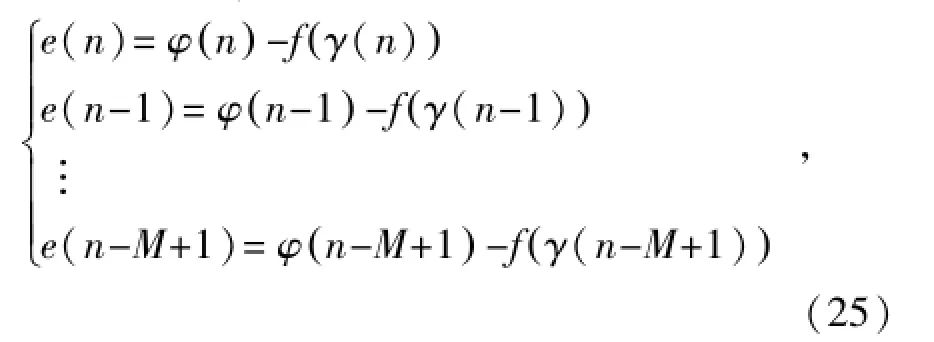
写成向量模型，可得

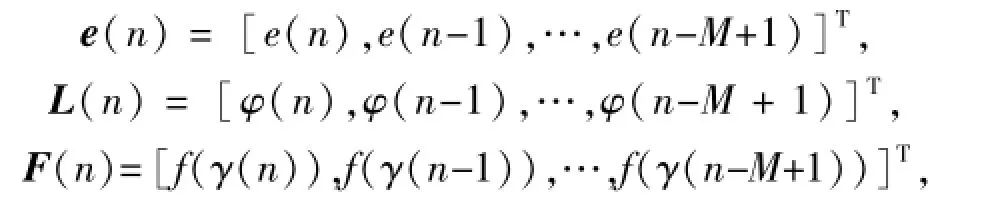
并且

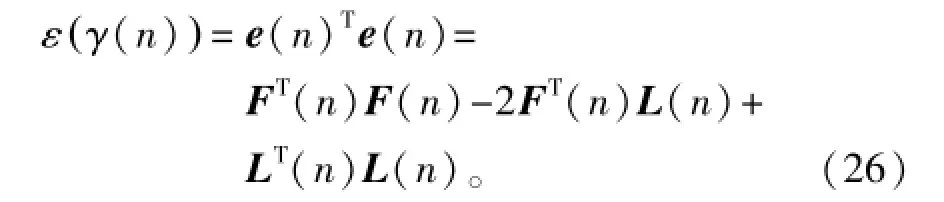
因为LT（n）L（n）是常量，ε（γ（n））的最小值为

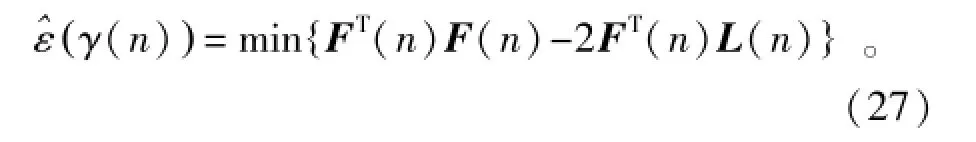
由于F（n）含有一系列未知参数的非线性函数，不能从其一阶导数中明确γ的表达式，对一阶导数赋0值的线性方法来获得理想γ值并不可行，因而采用改进的高斯-牛顿算法通过迭代估算第n时刻的γ值。基于最小二乘法的原理，γ的估算可表示为

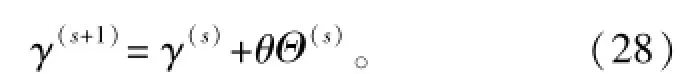
式中：Θ（s）＝JT（γ（s））J-1（γ（s））JT（γ（s））e（n）；s是迭代系数。并将计算所得的雅可比矩阵J（γ）＝[∂e1（n）/∂γ，…，∂eN-M＋1（n）/∂γ]T用于迭代。由于高斯-牛顿算法很大程度取决于初始值并会产生偏离，这里采用调整因子θ提高算法性能，并且设θ＝0.5能简化运算的同时，也能较好地满足实验的需要。迭代的停止条件为

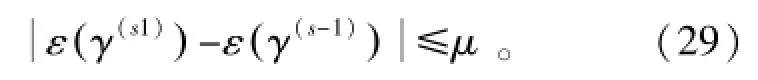
计算γ（n）的步骤如下：

（1）按提供的初始值计算Θ（0）和γ（0）；

（2）结合公式（26）与（28）计算γ（s）和εγ（s）；

（3）如果满足迭代的停止条件，则进行步骤4，否则返回步骤2；

（4）γ（s）是γ（n）的输出。

5 算法实现与试验验证

通过无人机的实际飞行获取实验数据，实验无人机装载1个GPS接收器和1个惯性测量单元（集成3个陀螺仪、1个三轴加速度计、3个磁力仪、1个压力传感器）。一个地面GPS基站提供参考节点信息。我们在一个空旷的草坪采集了12组射频信号数据。无线射频信号的收发通过两个802.11 b/g无线模块（GigabYte GN-WI01GT）完成。为了免受其他无线电波传输的影响，经过测试后无线模块的通信信道设定为2.462 GHz，发射功率设定为5 dBm，传输速率设定为1 Mb/s，采集范围控制在60 m以内。本文的实验环境设置与真实场景基本一致，无人机实验验证基于真实测试数据，差分GPS信号仅用于性能对比。

5.1 距离测量误差实验

本实验对测量的接收信号强度数据分别应用扩展卡尔曼滤波和最小二乘算法进行距离估算。在扩展卡尔曼滤波模型中，其迭代速率为10次/s，所有的算法都没有应用惯性测量单元所测信息。从图3可以看出，利用最小二乘算法估算无人机移动距离的误差变化较大，而利用扩展卡尔曼滤波算法估算的结果较稳定，并且估算精确度更高。这两种方法所产生的不同精度主要在于如何利用历史数据。最小二乘法使用当前和历史数据对系统建模，如果过程模型和观测模型有较大的瞬时差异，最小二乘法会产生大比例的误差，如图4所示。而卡尔曼滤波算法根据测量噪声方差对自己的参数进行调整，而且它仅观察有限而必要的部分，因而增强了对噪声瞬时变化的抵抗性。图4中的误差是通过估算距离和GPS定位系统所得位置的数据计算比较所得，当置信水平为80%时，通过卡尔曼滤波法所测的误差为4 m，最小二乘法所测的误差为10 m。随着无人机飞行距离变远，两种算法所测的误差也逐渐增大。

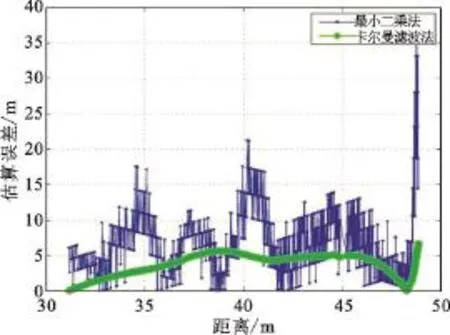
图3 从接收信号强度估算的无人机距离Fig.3 Estimation distance of a UAV from the received radio signal

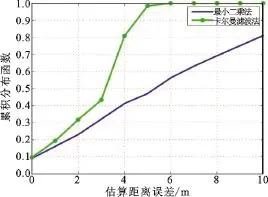
图4 两种算法的估算距离误差比较Fig.4 The comParison of estimation distance error betWeen tWo algorithms

5.2 噪声影响

由于有色噪声具有一定的规律性，在信号处理中容易除掉。在使用扩展卡尔曼滤波法估算时，如果只考虑白噪声的影响，那么距离估算误差将远远高于同时对白噪声和有色噪声进行处理后的结果，如图5所示。当置信水平为80%时，只处理白噪声所测的误差约为8.5 m，而根据公式（12）和（13）推导的卡尔曼滤波算法，同时处理白噪声和有色噪声所得的误差仅为4 m。值得提到的是，所得的差异并不总是相同的，还受到环境影响，如噪声方差等。

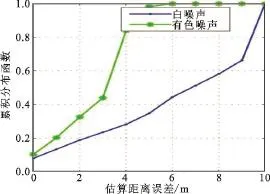
图5 白噪声和有色噪声对距离估算误差的影响Fig.5 Effects of White noise and color noise on distance estimation error

5.3 路径损耗因子影响

采用不同的路径损耗因子也会产生不同的距离估算误差，如图6所示。在测试的距离内，路径损耗因子值越高，估算性能越好。受无线传输路径上多种反射和衰减的影响，路径损耗因子在实际环境中极不稳定，本文提出的自适应路径损耗因子估计算法虽然不是具有最好的性能，但总体距离估算误差的结果处于比较稳定的水平，特别在置信水平大于70%时，其估算误差结果优于任何采用固定值的方法。

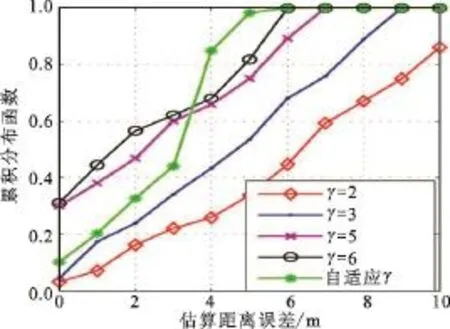
图6 路径损耗因子对距离估算误差的影响Fig.6 Effects of Path-loss factors on estimation error

5.4 惯性测量单元影响

惯性测量单元的信息主要反映了无人机的速率。当加入惯性测量单元所测信息后，距离估算的精确度有明显提高，如图7所示。当置信水平为80%时，使用惯性测量单元辅助所测的距离估算误差约为1.7 m，使用该方法的前提是惯性测量单元所测信息具有一定的准确性，这主要取决于惯性传感器的性能，其精确度通常随时间的增长而降低。

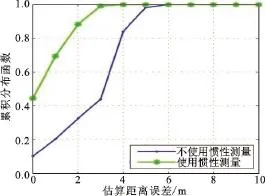
图7 惯性测量单元的信息辅助对距离估算误差的影响Fig.7 Effect of assistance of inertial measurement unit on distance estimation error

6 结束语

本文利用无线射频信号估算无人机的移动定位，主要提出了应用扩展卡尔曼滤波算法实现距离估算，通过对信号模型及噪声分量进行分析，较好地处理了有色噪声和路径损耗对距离估算的不良影响。此算法提高了无人机群移动定位的精度，可用于无人机协同传感或其他任务，使无人机得到了更广泛的应用。

相对于已有的算法，本研究工作提高了无人机定位的准确性和环境适应性。下一步工作将研究白噪声的消除和定位系统精度增强，对飞行姿态、天线特征和环境等影响因素进行具体分析和量化。

[1] TEACY W，NIE J，MCCLEAN S，et al.Maintaining con_ nectivitY in UAV sWarm sensing[C]//Proceedings of 2010 IEEE GLOBECOM WorkshoPs.Miami，USA：IEEE，2011：1771-1776.

[2] 杨润丰，骆春波，张智聪.适用于无人搜救机组的新型移动中继通信模型[J].电讯技术，2014，54（10）：1330-1334. YANG Runfeng，LUO Chunbo，ZHANG Zhicong.A Novel Mobile RelaY Communication Model for Search and Res_ cue UAVs[J].Telecommunication Engineering，2014，54（10）：1330-1334.

[3] BRYSON M，SUKKARIEH S.ObservabilitY analYsis and ac_ tive control for airborne SLAM[J].IEEE Transactions on AerosPace and Electronic SYstems，2008，4（1）：261-280.

[4] GOLDEN S，BATEMAN S.Sensor measurements for Wifi location With emPhasis on time-of-arrival ranging[J]. IEEE Transactions on Mobile ComPuting，2007，6（10）：185-1198.

[5] PATWARI N，HERO A O，PERKINS M，et al.Relative lo_ cation estimation in Wireless sensor[J].IEEE Transac_ tions on Signal Processing，2003，51（8）：2137-2148.

[6] WEISS A.On the accuracY of a cellular location sYstem based on RSS measurements[J].IEEE Transactions on Vehicular TechnologY，2003，52（6）：1508-1518.

[7] HAN J H，KWON J H，LEE I，et al.Position and attitude determination for UAV-based GPS，IMU and AT Without GCPs[C]//Proceedings of 2011 International WorkshoP on in Multi-Platform/Multi-Sensor Remote Sensing and MaPPing（M2RSM）.Xiamen：IEEE，2011：1-5.

[8] MOSHE B，SHVALB N，BAADANI J，et al.Indoor Positio_ ning and navigation for micro UAV drones[C]//Proceed_ ings of 2012 IEEE 27th Convention of Electrical＆Elec_ tronics Engineers in Israel.Eilat，Israel：IEEE，2012：1-5.

[9] BANDIERA F，COLUCCIA A，RICCI G.A cognitive al_ gorithm for received signal strength based localization [J].IEEE Transactions on Signal Processing，2015，63（7）：1726-1736.

[10] MENIEM M H A，HAMAD A M，SHAABAN E.Relative RSS-based GSM localization technique[C]//Proceedings of 2013 IEEE International Conference on Electro/Infor_ mation TechnologY.Indiana，USA：IEEE，2013：1-6.

[11] ALIZADEH P，CHEVALEYRE Y，ZUCKER J D.AP_ Proximate regret based elicitation in Markov decision Process[C]//Proceedings of 2015 IEEE International Conference on Research，Innovation，and Vision for the Future.Can Tho，Vietnam：IEEE，2015：47-52.

杨润丰（1979—），男，广东东莞人，2009年于英国雷丁大学获电子工程专业博士学位，现为副教授、教研室主任，主要研究方向为数字信号处理、无线通信；

YANG Runfeng Was born in Dongguan，Guandong Province，in 1979.He received the Ph.D.degree from UniversitY of Reading，UK， in 2009.He is noW an associated Professor and dean of teaching -research section.His research concerns digital signal Process_ ing and Wireless communication.

Email：Yangrf@dgPt.edu.cn

骆春波（1983—），男，重庆人，2011年于英国雷丁大学获电子工程专业博士学位，现为副教授，主要研究方向为数字信号处理、无线通信；

LUO Chunbo Was born in Chongqing，in 1983.He received the Ph.D.degree from UniversitY of Reading，UK，in 2011.He is noW an associated Professor.His research concerns digital sig_ nal Processing and Wireless communication.

Email：c.luo@exeter.ac.uk

张智聪（1980—），男，广东东莞人，2007年于清华大学获系统工程专业博士学位，现为教授，主要研究方向为系统工程；

ZHANG Zhicong Was born in Dongguan，Guangdong Prov_ ince，in 1980.He received the Ph.D.degree from Tsinghua Uni_ versitY in 2007.He is noW a Professor.His research concerns sYstem engineering.

Email：stePhen1998@gmail.com

李铭钊（1980—），男，天津人，2006年于英国华威大学获系统工程专业硕士学位，现为高级工程师，主要研究方向为系统工程。

LI Mingzhao Was born in Tianjin，in 1980.He received the M.S.degree from UniversitY of WarWick，UK，in 2006.He is noW a senior engineer.His research concerns sYstem engineering.

Email：limzh@cec.com.cn

UAV Positioning Based on Extended Kalman Filter Algorithm

YANG Runfeng1，LUO Chunbo2，ZHANG Zhicong3，LI Mingzhao4
（1.DePartment of Electronic Engineering，Dongguan PolYtechnic，Dongguan 523808，China；2.DePartment of Mathematics and ComPuter Science，UniversitY of Exeter，EX4 4QF，UK；3.School of Mechanical Engineering，Dongguan UniversitY of TechnologY，Dongguan 523808，China；4.China Electronics CorPoration，Beijing 100846，China）

Mobile Positioning is essential for Unmanned Aerial Vehicles（UAVs）to coPe With UAV mobilitY and the comPlexitY of dePloYed environments.To solve the Problem that UAVs'Global Positioning SYstem（GPS）signal fails，radio frequencY（RF）signal strength from the on-board communication module is a_ doPted.For the Processing of received signals，the extended Kalman filter（EKF）method is used to esti_ mate distance and the Least Square（LS）algorithm is used to estimate the Path loss factor.Theoretical a_ nalYsis and exPeriment results demonstrate that the ProPosed algorithms offer better Performance for enhan_ cing received signals under coloured noise and imProving distance estimation accuracY.Given a confidence level of 80%，the neW algorithm has imProved the estimation accuracY from 9.5 m to 4 m.The further en_ hancement With data fusion from the gYro information is also Provided.

unmanned aerial vehicle（UAV）；mobile Positioning；extended Kalman filter；distance estimation

The National Natural Science Foundation of China（No.71201026）；The Science and Technological Program for Dongguan’s Higher Education，Science and Research Institutions（2014106101034）；The Dongguan PolYtechnic Science and Research Funding ScholarshiP（2015b06）

TN925

A

1001-893X（2016）01-0060-07

10.3969/j.issn.1001-893x.2016.01.011

杨润丰，骆春波，张智聪，等.基于扩展卡尔曼滤波算法的无人机定位[J].电讯技术，2016，56（1）：60-66.[YANG Runfeng，LUO Chunbo，ZHANG Zhicong，et al.UAV Positioning based on extended Kalman filter algorithm[J].Telecommunication Engineering，2016，56（1）：60-66.]

2015-05-18；

2015-12-14 Received date：2015-05-18；Revised date：2015-12-14

国家自然科学基金资助项目（71201026）；东莞市高等院校、科研机构科技项目（2014106101034）；东莞职业技术学院科研基金项目（2015b06）

**通信作者：Yangrf@dgPt.edu.cn Corresponding author：Yangrf@dgPt.edu.cn