基于分布参数的区间粗糙数型MADM的TOPSIS方法

夏晓东,吕跃进

(广西大学数学与信息科学学院, 广西南宁530004)



基于分布参数的区间粗糙数型MADM的TOPSIS方法

夏晓东,吕跃进

(广西大学数学与信息科学学院, 广西南宁530004)

定义了带分布参数的区间粗糙数的运算法则,以期望值和方差集结函数的优劣度得到正负理想点，提出了一种积分形式的带分布参数型的区间粗糙数新的相离度,并根据已有的加权区间粗糙的距离平均算子(WIRDAA)概念,构建基于分布参数的区间粗糙数型MADM的TOPSIS方法。最后以一个实例说明该方法的可行性。

区间粗糙数;MADM;TOPSIS;排序方法

0 引 言

多属性决策(MADM)是考虑在多个属性或者指标下，从多个备选方案中选出最佳方案或对备选方案进行优劣排序的决策方法，该方法已运用到日常生活的诸多领域。现实生活中，因为经济方面的不确定性,元素本身含有模糊性,人们思维的局限性，决策信息通常有不确定性，其不确定性表现形式也是多元化的,灰色、模糊性、随机性、粗糙性等等，时常以灰数、模糊数、区间数、区间粗糙数等来表示决策信息。

1982年，波兰的Pawlak[1]提出粗糙集理论以来，其成果已被广泛地运用到决策分析、机器学习、数据挖掘与模式识别等许多方面。粗糙集是根据下近似和上近似来表现出概念，可以准确地刻画一些具有不确定性和模糊性的信息。2002年Liu[2]提出粗糙随机变量及区间粗糙数，粗糙随机变量是指取值于粗糙变量集合上的随机型变量，与此同时，Liu也更进一步提出了乐观值、悲观值、期望值算子、粗糙随机运算、机会测度、机会分布等概念及常用的几种粗糙规划模型。翁世洲等[3]提出了运用综合优势度阵法得到排序;王坚强等[4]根据加权的区间粗糙距离平均算子，构建优化模型求出权重进行方案的排序和择优；焦佳等[5]通过有序加权平均算法(OWA法)进行方案的排序与择优；朱方霞等[6]总结了区间多属性决策问题研究的主要成果；毛军军等[7]将混合集成算子运用到多属性决策中，这些都为区间粗糙数型多属性决策的研究提供了一些理论基础。

但是实际很多情形下，多属性决策中的属性取值可通过形如([a,b],[c,d])的区间粗糙数来表示，该表示可通过统计学的相关方法得到得。例如在房地产造价问题中，某房产的造价用一个区间粗糙数([30,70],[25,80])表示，其解释为该造价在25到80之间，而更大的可能落在在30到70这个区间。区间粗糙数还可以带有参数，如([a,b],[c,d],α)，其中α在0到1之间，表示以概率α取到内区间[a,b]。

2010年,曾玲等[8]提出一种区间粗糙数型多属性决策方法，该方法研究了不含参数的区间粗糙数型多属性决策问题,主要思路:首先给出粗糙属性值的规范化公式，然后基于区间粗糙数的相离度定义，建立以极大化属性值为目标的最优化模型来确定各属性权重，进而基于粗糙算术运算以及期望算子，计算出各方案的期望效用值，从而得到各方案排序。2013年,靳宗伟等[9]提出了一种基于区间粗糙算子的决策方法,解决了不含参数的区间粗糙数型多属性决策问题，而对于含参数的区间粗糙数的决策问题至今鲜有研究。

文献[8]提出了不含分布参数的区间粗糙数相离度，定义为两个区间粗糙数的对应的四端点差的绝对值相加，而该定义未能清晰反映区间粗糙数的实质，对于上下近似的相离度赋予相同的权重，不能清晰地刻画出区间粗糙数相离度的本质。

然而现今存在的问题是，尚未对带分布参数型区间粗糙数的多属性决策问题进行系统研究。鉴于此，本文总结前人已有的工作内容后，提出了基于积分形式的区间粗糙数新的相离度，运用理想解法求出属性权重，得到最终的评价值给多属性进行了排序，解决了先前的区间粗糙数相离度定义中不精确，容易丢失信息的问题，同时也为带分布参数型的区间粗糙随机多属性决策问题提供了新方法。

1 区间粗糙数

经典粗糙集是基于等价关系的，通过上近似与下近似两个精确集来描述任一个概念(集合)，当上下近似相等时该概念为精确集，否则为粗糙集。

定义4 一个区间粗糙数可视为下近似和上近似均为区间数的粗糙变量，记为([a,b],[c,d]),其中c≤a≤b≤d.并称[a,b]为内区间，[c,d]为外区间。

定义5 设ξi=([ai,bi],[ci,di])(i=1,2)为两个区间粗糙数，则有：

ξ1+ξ2=([a1+a2,b1+b2],[c1+c2,d1+d2])。

(1)

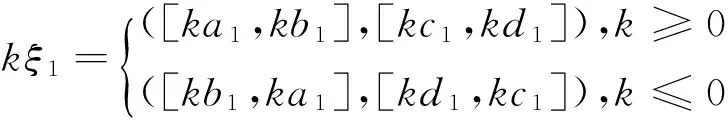
(2)

定义6 设ξ1={([a,b],[c,d],α)}为区间粗糙数[11]，则ξ1的期望值为:

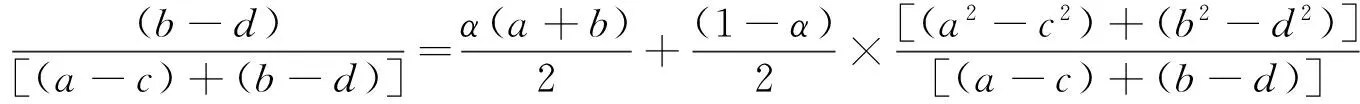
(3)

此外按照均匀分布下的方差计算公式，则有：

(4)

对于区间粗糙数，可按其期望值大小进行排序，即设ξ1和ξ2为两个区间粗糙数，则ξ1>ξ2当且仅当φ(E(ξ1),D(ξ1))≻φ(E(ξ2),D(ξ2))。

由期望—方差(M-V法)对区间粗糙数进行排序时，可由各自偏好使用期望和方差，不同的风险态度得到不同排序，也可通过构建集结函数φ(E(ξ),D(ξ))来对期望和方差进行集结。常见的集结函数形式如下：

(5)

式(5)中λ为显示期望与方差重要性的参数，由决策者的偏好决定。

定义7 设ξi=([ai,bi],[ci,di],αi)(i=1,2)(αi≥0.5)为两个区间粗糙数，默认它们四个端点取值至少有一个不同，即a1=a2,b1=b2,c1=c2.d1=d2不是同时成立。则它们的相离度定义为:

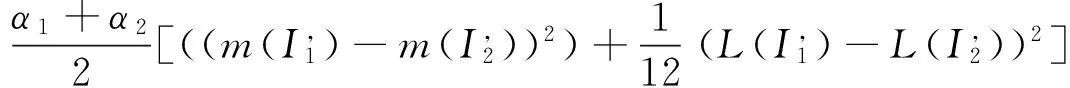
(6)

显然定义7具有以下性质(非负性，对称性及风险偏好性)：

①非负性:d(ξ1,ξ2)≥0,且当d(ξ1,ξ2)=0，当且仅当ξ1=ξ2。

②对称性:d(ξ1,ξ2)=d(ξ2,ξ1)。

③风险偏好性:偏重内区间的相离度。

对于已经规范化的分布参数型区间粗糙数,还具有以下性质:

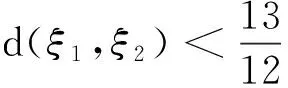
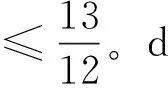
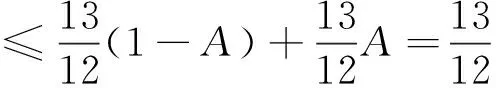
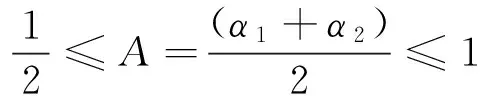
②确定性 对于任意的带分布参数型的区间粗糙数ξ1,ξ2，都能保留住大多数信息去度量出精确的相离度。

显然定义7相较于文献[3-5]中定义的区间粗糙数相离度而言，更好的保留了两个区间粗糙数的信息，可以看出还是偏重于下近似的相离度，更精确的体现了两个区间粗糙数的相离度，得到的结果比较客观。

2 含分布参数型区间粗糙数的WIRDAA算子的MADM模型

现有一个含分布参数的区间粗糙数多属性决策问题，设有m个方案A={a1,a2,…,am}n个决策属性C={C1,C2,…,Cn},各属性相互独立,则对应的权向量为W=(w1,w2,…,wn),wj∈[0,1],j∈(1,2…,n),w1+w2+…wn=1,W信息是不完全的。

ai关于cj的属性取值为区间粗糙变量ξij，可以构成区间粗糙决策矩阵M=(ξij)m×n,在各属性权重是模糊不定的情况下，制定方法去确定方案集A={a1,a2,…an}的最优排序。

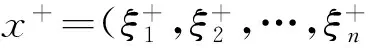
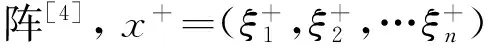
(7)

定义fw为加权的区间粗糙距离平均算子，又称为WIRDAA算子。显而易见，fw值越小，显示出方案ai与正理想点方案之间的距离越小，进而表达出ai越优。

根据上述分析，建立一个线性规划模型来求解属性权重值，有:

(8)

同理,也可以构建一个离负理想点越远越好的线型规划模型:

(9)

通过一系列分析，本文提出一种含分布参数型区间粗糙数的WIRDAA算子的MADM模型,上述分析的建模步骤如下：

Step 1 由定义6，逐步对方案在各个属性下的决策取值求解它们的期望和方差，得到M-V矩阵。

Step 2 对信息进行规范化，决策属性有效益性和成本型两种，为了消除量纲影响，可以给出区间粗糙属性值的规范化公式进行规范化，一般运用极差转换法：

由上述的公式知，通过规范化处理之后的属性取值仍为区间粗糙数，ai在属性cj下的属性值仍记为ξij=([aij,bij],[cij,dij],α)，由此可得规范化的决策矩阵：

Step 4 集结方案属性值，利用WIRDAA算子对方案ai的属性值进行集结，得到ai的综合评价值Zi+,Zi-,i=1,2,…,m；

3 实例分析

在建设工厂的选址中，假定某公司正对5个候选地址(x1,x2,x3,x4,x5)进行研究，考察期间，主要考虑节约成本(a1),预期收益(a2),管理效益(a3),风险避免(a4)这四个方面因素,并希望从5个候选地址中选出最优方案。具体的评估数据如下表所示(表中的数据均为效益型指标)

表1 候选地址的评估数据表

运用期望方差公式，即式(3)和式(4)得到信息表的M-V矩阵:

规范化之后的矩阵如下：

计算出与正理想点最近的相离度矩阵D+为:

同理通过计算与负理想点最远的相离度矩阵D-如下：

最终排序结果是53124，这与文献[5]一致，但是保留了大多数信息。本文给出了一个基于分布参数型区间粗糙数的MADM的理想解法模型，既考虑了下近似和上近似相离度比重的侧重，又考虑了与正理想点最近和负理想点最远的TOPSIS模型。有效解决了带参数分布的区间粗糙数型多属性实际决策问题。

4 结 语

本文定义了一种带参数型区间粗糙数之间的相离度，该定义很大程度的保留了每个属性值的全部信息，在求解每个方案点到正负理想点的距离的时候是很客观地反映相离的程度，相较于文献[4]来说更加客观了，不是简单将对应的四个端点做差取绝对值做和。这样得到的综合评价值也是较为精确的，属于一种兼顾区间粗糙数型属性值的上近似和下近似的精确度量方式。通过与正理想点最近和负理想点最远兼顾而得到的规划模型，得到属性权重，进而解出综合评价值，最终得到排序结果也较文献[8]更加有理论依据，更加合理，更加体现了区间粗糙数的内涵，构建了很精确的模型去求解实际问题。

[1] PAWLAK Z.Roughsets[J]. Int J of informationand Computer Science, 1982,11(5):341-356.

[2] LIU B.Theory and practice of uncertain programming[M]. Heidelberg:Physica-verlag, 2002.

[3] 翁世洲，吕跃进.区间粗糙数的排序方法及其应用[J]. 南京大学学报(自然科学版),2015，51(4)：818-825.

[4] 王坚强，唐平.基于区间粗糙算子的粗糙随机多属性决策方法[J]. 控制与决策,2011，26(7)：1056-1064.

[5] 焦佳，周庆健.属性值为区间数的多属性决策OWA算法[J]. 大连民族学院学报, 2013，15(3)：276-279.

[6] 朱方霞，陈华友.区间多属性问题研究综述[J]模糊系统与数学, 2013,27(3)：149-159.

[7] 毛军军，徐丹清.基于集成算子的改进IITFN多属性群决策方法[J]. 计算机工程与应用, 2013，49(12):53-56.

[8] 曾玲，曾祥艳.一类区间粗糙数型多属性决策方法研究[J]. 控制与决策,2010，25(11)：1757-1760.

[9] 靳宗伟，郭恒.基于理想点的区间粗糙数型多属性决策方法[J]. 重庆理工大学学报,2013，27(5):113-117.

[10]LIU B.Uncertain theory:An introduction to its axiomatic foundation[M]. Berlin:Springer-Verlag,2004.

[11]SLOWINSKI R,VANDERPOOTEN D.A generalized definition of rough approximations based on similarity[J]. IEEE Trans on Konwledge and Data Engineering,2000,12(2):331-336.

(责任编辑 梁碧芬)

TOPSIS method based on MADM of the interval rough numbers with distributed parameter

XIA Xiao-dong, LYU Yue-jin

(College of Mathematics and Information Science,Guangxi University, Nanning,53004)

The paper defines the algorithm of interval rough numbers with distributed parameter. From the advantages and disadvantages of an aggregation function with the expectation value and variance, it finds the positive and negative ideal points. What’s more, it proposes a kind of deviation degree of interval rough numbers with distributed parameter in an integral form. By means of the concept of the existing rough weighted interval distance averaging operator (WIRDAA), it also builds a TOPSIS method based on MADM of the interval rough numbers with distributed parameter. Finally the feasibility of the method is illustrated by an example.

interval rough numbers; MADM;TOPSIS;ranking method

2016-06-23；

2016-07-28

国家自然科学基金资助项目(71361002);广西自然科学基金资助项目(2013GXNSFAA19016)

吕跃进(1958—)，男，广东龙川人，广西大学教授；E-mail:lvyjin@126.com。

夏晓东,吕跃进.基于分布参数的区间粗糙数型MADM的TOPSIS方法[J].广西大学学报(自然科学版)，2016，41(5)：1603-1609.

10.13624/j.cnki.issn.1001-7445.2016.1603

O21;C934

A

1001-7445(2016)05-1603-07